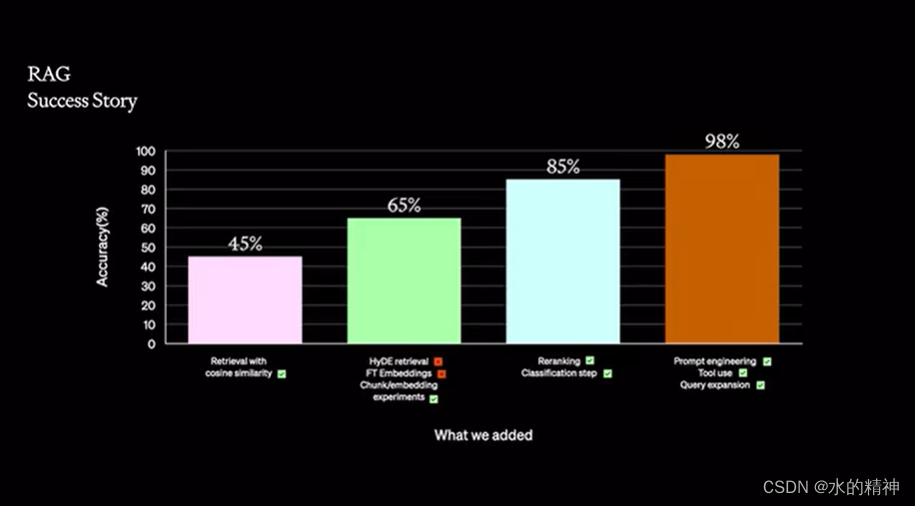
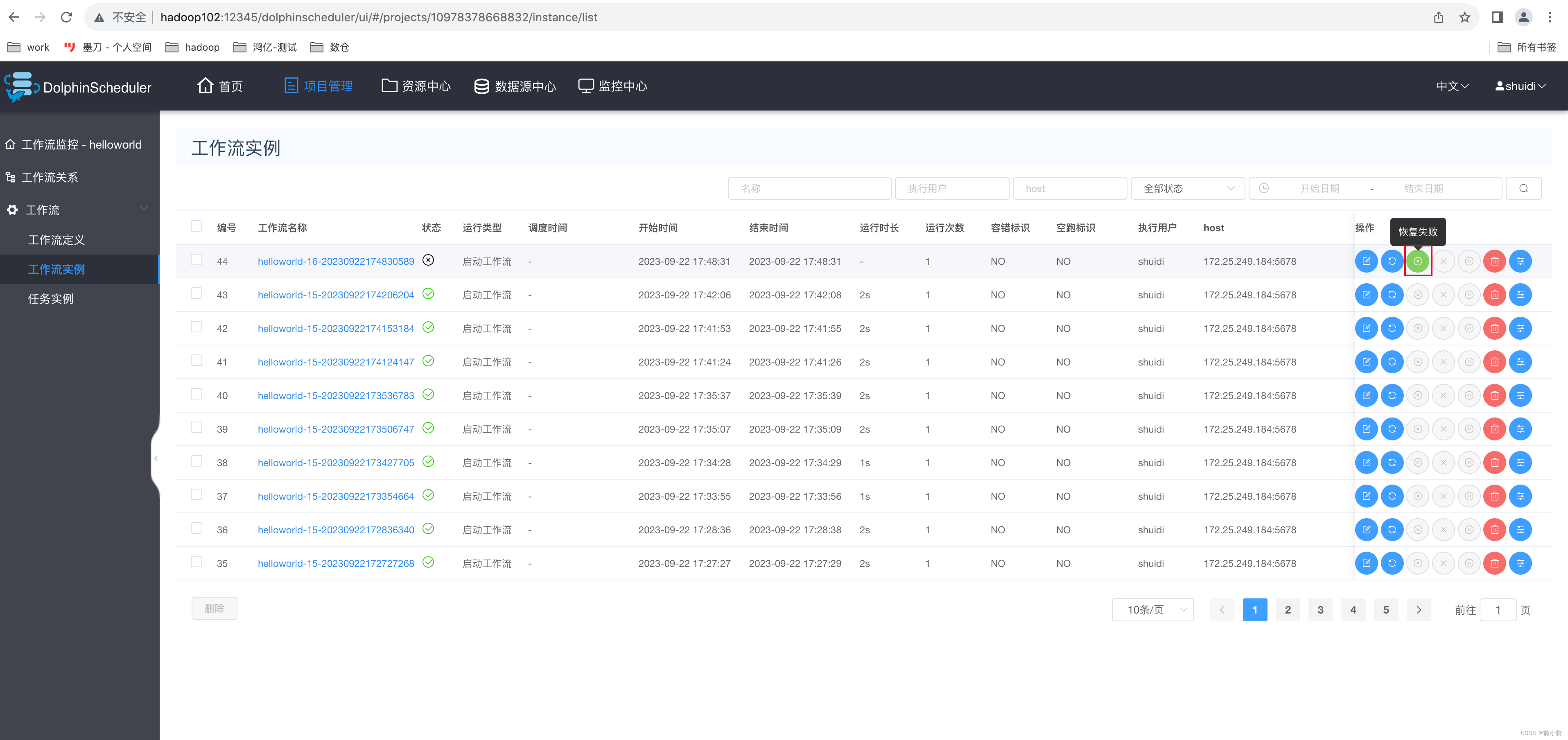
无人驾驶卡尔曼滤波(行人检测)
x
k
=
a
x
k
−
1
+
w
k
x_k = ax_{k-1} + w_k
xk=axk−1+wk
w
k
w_k
wk:过程噪声
状态估计
估计飞行器状态(高度)
x
k
=
z
k
−
v
k
x_k = z_k - v_k
xk=zk−vk
卡尔曼滤波通过同时考虑上一状态值和当前的测量值来获得对当前状态值的估计,对状态
x
x
x的估计:
x
^
\hat{x}
x^
x
^
k
=
x
^
k
−
1
+
g
k
(
z
k
−
x
^
k
−
1
)
\hat{x}_k = \hat{x}_{k-1} + g_k(z_k - \hat{x}_{k-1})
x^k=x^k−1+gk(zk−x^k−1)
g
k
g_k
gk:卡尔曼增益:指之前的估计和当前测量对当前估计的影响的分配权重,如果为0,说明非常不信任当前的测量,直接保留了上一次的估计作为当前状态的估计;增益为 1,认为当前的测量非常可信,彻底接受它作为我当前状态的估计
计算卡尔曼增益
那么如何计算卡尔曼增益呢?我们使用一种间接的方法,我们虽然不知道测量噪声 v k v_k vk的值,但是我们知道它的均值,前面我们提到,测量噪声来自传感器本身,并且符合高斯分布,所以我们能够从传感器厂商那里获得测量噪声的均值 r r r,那么 g k g_k gk可以表示为:
g k = p k − 1 ( p k − 1 + r ) g_k = \frac{p_{k-1}}{(p_{k-1} + r)} gk=(pk−1+r)pk−1
p k p_k pk:预测误差
p k = ( 1 − g k ) p k − 1 p_k = \frac{(1 - g_k)}{p_{k-1}} pk=pk−1(1−gk)
那么假设前一次的预测误差 $ p_{k-1} = 0$,那么根据公式,当前的增益
g
k
=
0
g_k = 0
gk=0,一维着舍弃掉当前的测量而完全采用上一个时刻的估计,如果
p
k
−
1
=
1
p_{k-1} = 1
pk−1=1 那么增益变成 1 / ( 1 +
r
r
r ) 通常$ r $ 是个很小的数值,所以增益为1,所以完全接受这一次的测量作为我们的估计(因为上一次的的预测误差太大了,为1,所以一旦拿到了新的测量,如获至宝,就干脆把不准确的上次的估计舍弃掉了)
对于下面的公式的分析是一样的,我们考虑极端的例子,当增益为 0,
p
k
=
p
k
−
1
p_k = p_{k-1}
pk=pk−1 ,因为我们彻底舍弃掉了本次的测量,所以本次的预测误差只能接受上一次的。
预测和更新
得到两个公式:
x k = a x k − 1 x_k = ax_{k-1} xk=axk−1
x ^ k = x ^ k − 1 + g k ( z k − x ^ k − 1 ) \hat{x}_k = \hat{x}_{k-1} + g_k(z_k - \hat{x}_{k-1}) x^k=x^k−1+gk(zk−x^k−1)
第一个公式我们称之为预测,是基于一些先验的知识(比如说运动模型,牛顿力学等等)觉得我们的状态应该是这样的,而第二个公式呢,就是我们基于我们“不完美的”的传感器的测量数据来更新我们对状态的估计。另为,预测,理论上只考虑了一个固定的过程模型和过程噪声,但是由于我们现在是对机械的状态进行估计,在预测过程中需要对机械本身的控制建模, 我们在预测部分再新增一个控制信号,我们用 b u k bu_k buk表示。实际的传感器测量除了会有测量噪声 v k v_k vk 以外,还会存在一定的关于真实状态的缩放,因此我们使用 x k x_k xk 表示测量时通常还会在其前面加一个缩放系数 c c c 。 结合这写我们就可以得到卡尔曼滤波预测和更新过程了:
预测
x ^ k = a x ^ k − 1 + b u k \hat{x}_k = a\hat{x}_{k-1} + bu_k x^k=ax^k−1+buk
p k = a p k − 1 a p_k = ap_{k-1}a pk=apk−1a
卡尔曼滤波更新的过程为:
g k = p k c c p k c + r g_k = \frac{p_kc}{cp_kc + r} gk=cpkc+rpkc
x ^ k ← x ^ k + g k ( z k − c x ^ k ) \hat{x}_k←\hat{x}_k + g_k(z_k - c\hat{x}_k) x^k←x^k+gk(zk−cx^k)
p k ← ( 1 − g k c ) p k p_k←(1 - g_kc)p_k pk←(1−gkc)pk
线性代数方法
预测
x ^ k = A x ^ k − 1 + B u k \hat{x}_k = A\hat{x}_{k-1} + Bu_k x^k=Ax^k−1+Buk
P k = A P k − 1 A P_k = AP_{k-1}A Pk=APk−1A
卡尔曼滤波更新的过程为:
G k = P k C c P k C + R G_k = \frac{P_kC}{cP_kC + R} Gk=cPkC+RPkC
x ^ k ← x ^ k + G k ( z k − C x ^ k ) \hat{x}_k←\hat{x}_k + G_k(z_k - C\hat{x}_k) x^k←x^k+Gk(zk−Cx^k)
P k ← ( 1 − G k C ) P k P_k←(1 - G_kC)P_k Pk←(1−GkC)Pk
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from sympy import Symbol, Matrix
from sympy.interactive import printing
x = np.mat([[0.0, 0.0, 0.0, 0.0]]).T
print(x, x.shape)
P = np.diag([1000.0, 1000.0, 1000.0, 1000.0])
print(P, P.shape)
dt = 0.1
F = np.mat([[1.0, 0.0, dt, 0.0], # 预测矩阵
[0.0, 1.0, 0.0, dt],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]])
print(F, F.shape)
H = np.mat([[0.0, 0.0, 1.0, 0.0], # 测量矩阵
[0.0, 0.0, 0.0, 1.0]])
print(H, H.shape)
ra = 0.09
R = np.mat([[ra, 0.0],
[0.0, ra]])
print(R, R.shape)
I = np.eye(4)
print(I, I.shape)
sv = 0.5
G = np.mat([[0.5*dt**2], # 卡尔曼增益
[0.5*dt**2],
[dt],
[dt]])
Q = G*G.T*sv**2 # 过程噪声的协方差矩阵
print(G, G.shape)
print(Q, Q.shape)
printing.init_printing()
dts = Symbol('dt')
Qs = Matrix([[0.5*dts**2], [0.5*dts**2], [dts], [dts]])
Qs*Qs.T
m = 200
vx = 20
vy = 10
mx = np.array(vx + np.random.randn(m))
my = np.array(vy + np.random.randn(m))
measurements = np.vstack((mx, my))
print(measurements.shape)
print('Standard Deviation of Acceleration Measurements=%.2f' % np.std(mx))
print('You assumed %.2f in R.' % R[0, 0])
# fig = plt.figure(figsize=(16, 5))
# plt.step(range(m), mx, label='$\dot x$')
# plt.step(range(m), my, label='$\dot y$')
# plt.ylabel('Velocity $m/s$')
# plt.title('Measurements')
# plt.legend(loc='best', prop={'size': 18})
xt = []
yt = []
dxt = []
dyt = []
Zx = []
Zy = []
Px = []
Py = []
Pdx = []
Pdy = []
Rdx = []
Rdy = []
Kx = []
Ky = []
Kdx = []
Kdy = []
def savestates(x, Z, P, R, K):
xt.append(float(x[0]))
yt.append(float(x[1]))
dxt.append(float(x[2]))
dyt.append(float(x[3]))
Zx.append(float(Z[0]))
Zy.append(float(Z[1]))
Px.append(float(P[0, 0]))
Py.append(float(P[1, 1]))
Pdx.append(float(P[2, 2]))
Pdy.append(float(P[3, 3]))
Rdx.append(float(R[0, 0]))
Rdy.append(float(R[1, 1]))
Kx.append(float(K[0, 0]))
Ky.append(float(K[1, 0]))
Kdx.append(float(K[2, 0]))
Kdy.append(float(K[3, 0]))
for n in range(len(measurements[0])):
x = F * x
P = F * P * F.T + Q
S = (H * P * H.T) + R
K = (P * H.T) * np.linalg.pinv(S)
Z = measurements[:, n].reshape(2, 1)
y = Z - (H * x)
x = x + (K * y)
P = (I - (K * H)) * P
savestates(x, Z, P, R, K)
def plot_x():
fig = plt.figure(figsize=(16, 9))
plt.step(range(len(measurements[0])), dxt, label='$estimateVx$')
plt.step(range(len(measurements[0])), dyt, label='$estimateVy$')
plt.step(range(len(measurements[0])), measurements[0], label='$measurementVx$')
plt.step(range(len(measurements[0])), measurements[1], label='$measurementVy$')
plt.axhline(vx, color='#999999', label='$trueVx$')
plt.axhline(vy, color='#999999', label='$trueVy$')
plt.xlabel('Filter Step')
plt.title('Estimate (Elements from State Vector $X$)')
plt.legend(loc='best', prop={'size': 11})
plt.ylim([0, 30])
plt.ylabel('Velocity')
plt.show()
def plot_xy():
fig = plt.figure(figsize=(16, 16))
plt.scatter(xt, yt, s=20, label='State', c='k')
plt.scatter(xt[0], yt[0], s=100, label='Start', c='g')
plt.scatter(xt[-1], yt[-1], s=100, label='Goal', c='r')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Position')
plt.legend(loc='best')
plt.axis('equal')
plt.show()
if __name__ == '__main__':
plot_xy()