并查集的路径压缩两种方法

法一

• 沿着路径查询过程中，将非根节点的值都更新为最后查到的根节点

int find(int x)
{
    if (p[x] != x) 
    	p[x] = find(p[x]);
    return p[x];
}

法二

int find_root(int x)
{
    int root = x;
    while(ufs[root] >= 0)
        root = ufs[root];
    while(ufs[x] >= 0)
    {
        int parent = ufs[x];
        ufs[x] = root;
        x = parent;
    }
    return root;
}

AcWing 240. 食物链

https://www.acwing.com/problem/content/description/242/

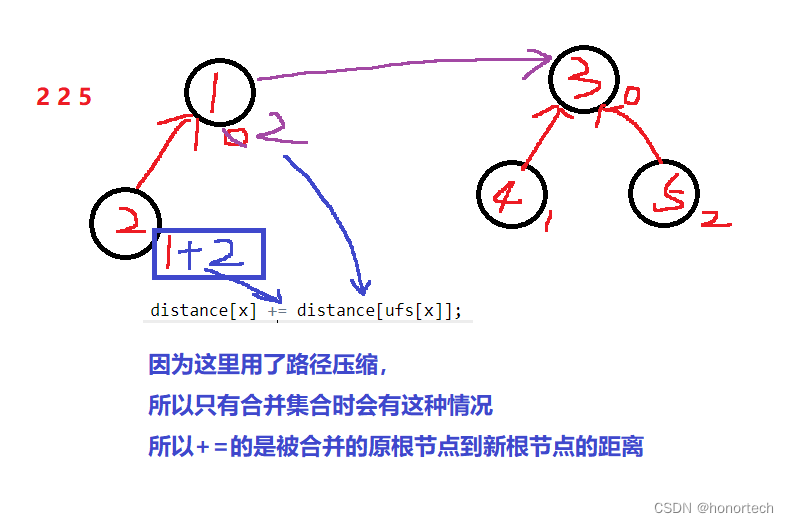
• 此题增加了每一个节点的权重，即其到根节点的距离
• 以此距离来判断该节点的动物种类
  

#include <iostream>

using namespace std;
const int N = 5e4 + 10;

int n, k, ufs[N], d[N];

int find_root(int x)
{
    if(x != ufs[x])
    {
        int tmp = find_root(ufs[x]);
        // 这里考虑发生集合合并的情况
        // 因为这里用了路径压缩，
        // 所以只有合并集合时会有这种情况
        // 所以+=的是被合并的原根节点到新根节点的距离
        d[x] += d[ufs[x]];
        ufs[x] = tmp;
    }
    return ufs[x];
}

int main()
{
    cin >> n >> k;
    for(int i = 0; i < n; ++i)
        ufs[i] = i;
    int ret = 0;
    while(k--)
    {
        int t, a, b;
        // cin >> t >> a >> b;
        scanf("%d%d%d", &t, &a, &b);
        if(a > n || b > n)
        {
            ret++;
            continue;
        }
        int ra = find_root(a), rb = find_root(b);
        if(t == 1)
        {
            if(ra == rb && (d[a] - d[b]) % 3)
                ret++;
            else if(ra != rb)
            {
                ufs[ra] = rb;
                d[ra] = d[b] - d[a];
            }
        }
        else
        {
            // 根相同，判断距离
            if(ra == rb && (d[a] - d[b] - 1) % 3)
                ret++;
            // 根不同，合并两集合
            else if(ra != rb)
            {
                ufs[ra] = rb;
                d[ra] = d[b] - d[a] + 1;
            }
        }
    }
    printf("%d", ret);
    return 0;
}

AcWing 837. 连通块中点的数量

示例并查集

#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int p[N], cnt[N];
int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        cnt[i] = 1;
    }
    while (m -- )
    {
        string op;
        int a, b;
        cin >> op;
        if (op == "C")
        {
            cin >> a >> b;
            a = find(a), b = find(b);
            if (a != b)
            {
                p[a] = b;
                cnt[b] += cnt[a];
            }
        }
        else if (op == "Q1")
        {
            cin >> a >> b;
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
        else
        {
            cin >> a;
            cout << cnt[find(a)] << endl;
        }
    }
    return 0;
}

自写并查集

#include <iostream>
#include <vector>
using namespace std;
const int N = 1e5 + 10;
int n, m;
vector<int> ufs(N, -1);
int find_root(int x)
{
    int root = x;
    while(ufs[root] >= 0)
        root = ufs[root];
    // 路径压缩，不然会超时
    while(ufs[x] >= 0)
    {
        int parent = ufs[x];
        ufs[x] = root;
        x = parent;
    }
    return root;
}
void union_set(int a, int b)
{
    int ra = find_root(a), rb = find_root(b);
    if(abs(ufs[ra] > abs(ufs[rb])))
        swap(ra, rb);
    if(ra != rb)
    {
        ufs[rb] += ufs[ra];
        ufs[ra] = rb;
    }
}

void find_union(int a, int b)
{
    int ra = find_root(a), rb = find_root(b);
    if(ra == rb)
        cout << "Yes" << endl;
    else
        cout << "No" << endl;
}

void count_set(int x)
{
    int r = find_root(x);
    cout << abs(ufs[r]) << endl;
}
int main()
{
    cin >> n >> m;
    string op;
    int a, b;
    while(m--)
    {
        cin >> op >> a;
        if(op == "C")
        {
            cin >> b;
            union_set(a, b);
        }
        else if(op == "Q1")
        {
            cin >> b;
            find_union(a, b);
        }
        else
            count_set(a);
    }
    return 0;
}