客观地说,没有数学就没有当前的大语言模型、多模态大模型,甚至压根就没有人工智能。对人工智能而言,数学就是“天”!但是,对于人类智能而言,数学虽然起到了很重要的作用,同样也起到了阻碍作用,也就是说单纯用现有数学工具体系是解不开人类智能这组“方程”的,即在人类智能中1+1可以不等于2。下面将对这两方面问题简要做个分析。
1、与大模型相关的数学知识
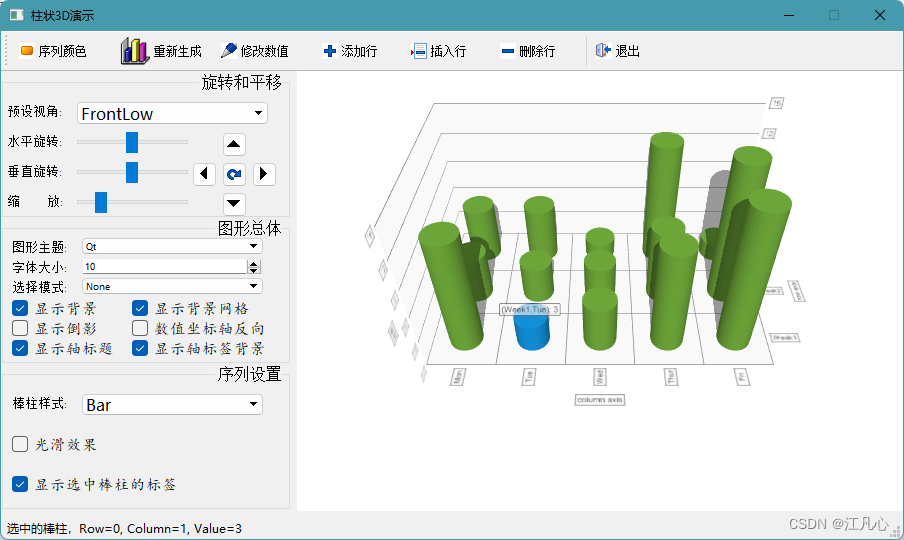
大模型通常涉及大规模的矩阵运算,线性代数是进行矩阵运算的基础。例如,大规模线性回归、主成分分析(PCA)等算法都涉及到矩阵的操作。大模型通常使用矩阵乘法来处理输入数据和模型参数之间的映射关系,矩阵乘法可以描述为两个矩阵相乘的操作,其中一个矩阵代表输入数据,另一个矩阵代表模型参数;在大模型中,常常需要对向量和矩阵进行加法和减法运算,以进行参数的更新和梯度的计算;大模型中的矩阵通常具有特征值和特征向量这两个重要的属性,特征值描述了矩阵的缩放特性,而特征向量描述了矩阵的变换方向;奇异值分解是一种常用的矩阵分解方法,可以将一个矩阵分解为三个矩阵的乘积,其中一个矩阵代表了矩阵的缩放特性,另外两个矩阵代表了矩阵的变换方向;矩阵的迹描述了一个方阵沿对角线元素的总和,而行列式描述了一个方阵的缩放特性。
与大模型相关的微分与积分知识在大规模模型的建模、优化、控制等方面起着重要作用,并且与概率论、统计学等知识相结合,共同应用于各个领域的问题求解,具体包括:
微分:微分是求函数在某一点处的变化率的一种数学操作。在大模型中,微分常用于优化问题,通过求解函数的导数来找到函数取极值的点。例如,在机器学习中,通过计算损失函数对参数的偏导数,可以进行梯度下降等优化算法。
偏导数:偏导数是多元函数对某个自变量的偏导数。在大模型中,我们通常需要处理多个变量之间的关系,因此偏导数是非常重要的。例如,在神经网络中,我们需要计算损失函数对于各个权重参数的偏导数,以便进行反向传播算法更新参数。
积分:积分是对函数的求和操作,表示函数在一定区间内的累积变化量。在大模型中,积分常用于概率密度函数的求解、面积估计等问题。例如,在概率论中,我们可以通过对概率密度函数进行积分来计算事件的概率。
不定积分:不定积分是对函数的原函数求解。在大模型中,我们经常需要对复杂函数进行求导操作,而不定积分可以帮助我们找到函数的原函数,从而进行更方便的求导计算。
定积分:定积分是对函数在一定区间内的积分操作。在大模型中,我们可以利用定积分来计算面积、体积、期望等量。例如,在统计学中,我们可以通过对概率密度函数进行定积分来计算随机变量的期望值。
微分方程:微分方程描述了函数与其导数之间的关系。在大模型中,微分方程经常出现在动态系统建模和控制问题中。例如,在机器人控制中,我们可以通过建立机器人的运动微分方程,来实现对机器人的轨迹控制和运动规划。
另外,大模型往往还需要进行概率建模和统计分析,例如,在大规模机器学习中,常用的算法如朴素贝叶斯分类器、随机森林等都涉及到概率论和统计学的知识;需要通过数值优化方法求解最优化问题,数值优化方法包括梯度下降、牛顿法、拟牛顿法等,这些方法都是对数学优化理论的应用;同时,大模型往往可以用图来表示,比如大规模网络分析、社交网络分析等,图论可以提供一些关于大模型的结构和关系的数学工具,如图的遍历算法、图的聚类算法等;最后,大模型中经常涉及到随机性和不确定性,随机过程理论可以用来描述和分析随机现象的数学模型,如马尔可夫链、随机漫步等。以上是与大模型相关的一些常见数学知识,实际应用中还可能涉及到其他领域的数学知识,如控制论、信息论等。
2、与人类智能相关数学知识的局限性
尽管数学在解决现实问题和推动科学发展方面发挥了重要作用,但与人类的智能相比,仍然存在许多本质上的限制。
首先,数学知识是基于严密的、形式化的推理和逻辑的,它关注于符号和公式之间的关系,而不关注与现实世界的直接联系,所以,数学知识在处理复杂的、模糊的、不确定的现实问题时可能显得力不从心。其次,数学知识通常是静态的,它建立在一系列已知的公理和定义之上,并通过逻辑推理进行推导,然而,现实世界是动态的、复杂的,常常涉及到不确定性和变化,因此,数学知识在处理现实问题时可能需要进行额外的抽象和假设,从而丧失一定的准确性和适应性。再者,数学知识往往是领域专业化的,不同领域的数学知识有着不同的应用范围和适用条件,数学知识在处理复杂的跨学科问题时可能需要结合其他学科的知识和方法,才能得到更好的结果。最后,数学知识在某些情况下可能存在局限性,例如,在处理非线性问题、混沌系统、复杂网络等复杂系统时,传统的数学方法可能无法完全描述和解释系统的行为。此外,在处理人类认知和智能时,数学知识可能无法完全涵盖人类的情感、主观意识、价值观等方面。
线性代数中,矩阵特征值和特征向量的变换和缩放分析主要应用于线性变换和线性代数的领域。它们描述了线性变换对向量空间的影响,包括缩放、旋转、拉伸等变换。在这种情况下,特征值表示变换的缩放因子,特征向量表示变换后的方向,它们提供了一种有效的方法来描述和分析语音识别、信号处理、图像处理等。而人类智能中的变换和缩放更多涉及到非线性的、复杂的变换过程,人类智能具有高度的适应性和灵活性,可以对输入进行感知、理解、推理、创造等多种非线性操作,这些操作不仅仅是简单的缩放或旋转,还包括语义理解、情感表达、意识等复杂的认知过程,即在人类智能中,缩放特性和变换方向与矩阵特征值和特征向量的描述是不同的,人类智能更强调对环境和任务的理解与适应能力,以及对输入数据的处理和分析能力。此外,人类智能的变换和缩放也受到更广泛的因素影响,如文化、社会背景、情感状态等,这些因素使得人类智能具有个体差异和多样性,不同的人在面对相同的输入时可能会表现出不同的变换和缩放行为。
人类认知的微分与数学的微分的最大区别在于它包含了价值性的考量。数学的微分主要关注变化的速率和趋势(如速度、加速度等),而人类认知的微分涉及到对客观事实的变化状况的理解(假设一个人正在准备购买一台新电视,在这个问题中,客观事实的变化状况包括不同电视的价格、品牌和规格等。通过比较不同电视的特点和价格,人们可以选择最适合自己需求和预算的电视。这里的微分认知涉及到客观事实的比较和变化),同时还考虑了价值性的尺度优化(例如,一个人想要减肥并提高健康水平。在这个问题中,价值性的尺度优化涉及到权衡不同行为的利益和代价。人们需要评估各种不同的饮食和锻炼计划,以找到最适合自己的方案。这里的微分认知涉及到对不同选项的评估和优化)。在人类认知的微分中,事实性的变化可以看作是客观客观事实的损失函数,当我们认知到一些事实的变化时,我们会评估其对我们的知识体系和理解的影响,这可以看作是一种事实性的损失函数。同时,人类认知的微分也考虑到了价值性的损失函数,人类认知的过程中,我们常常会根据自己的价值观与道德观念,对事实的变化进行评估和判断,例如,在做出决策时,我们会考虑到不同选择的利弊,以及它们符合我们的价值观的程度。这可以看作是一种价值性的损失函数。另外,人类认知的微分还涉及到事实与价值混合的损失函数,例如,一个人正在考虑是否要辞去一份高薪工作去追求自己的梦想。在这个问题中,事实性的损失函数涉及到辞去工作后可能失去的稳定收入和职业发展机会。价值性的损失函数涉及到放弃自己的梦想可能带来的后悔和不满。通过权衡这些损失函数,人们可以做出最终的决策。在实际情况中,事实与价值往往是相互交织的,我们的认知过程也会同时考虑它们。例如,在评估一个科学理论时,我们除了要考虑其与已有事实的一致性,还要考虑其对我们的价值观的影响,这种混合的损失函数需要综合考虑事实和价值的多个维度。
数学的积分是一种数学工具,用于求解函数的累积变化量。它主要关注于客观事实的累积变化量,即函数在某一区间上的面积或曲线下的面积。数学积分可以帮助我们计算物理学中的速度、加速度、面积、体积等问题。与数学的积分相比,人类认知的积分更加复杂,涉及到客观事实的累积变化量、价值性的累积变化量以及事实与价值混合的累积变化量,这些方面共同构成了人类对世界的认知和理解。人类在认知过程中,通过积累和整合客观事实,逐渐形成自己的知识体系和认知模式,如人类在科学研究、观察和实验中积累了大量的客观事实,通过不断观察和记录,已经了解到地球绕着太阳公转、水的沸点是100摄氏度等等,这些客观事实的积累使得人类对于自然规律和现象有了更深入的认识。另一方面,人类的认知积分还包括价值性的累积变化量,如人类对于道德、伦理和美学等价值领域也有着积累的认知,通过历史的发展和社会的进步,人类逐渐形成了各种价值观和道德准则,如尊重他人的自由和权利、平等、公正等,这些价值性的认知积累使得人类能够更好地判断和行动,推动社会的进步和发展。此外,人类的认知积分还包括事实与价值混合的累积变化量,在很多领域中,客观事实和价值观念是相互交织的,例如,生物伦理学中的人类基因编辑技术,既涉及到科学事实(人类基因组的结构和功能),又涉及到价值判断(是否应该进行基因编辑),人类的认知在这些领域中的积分既包括对基础事实的了解,也包括对伦理和道德问题的思考和决策。
综上所述,尽管数学知识在解决许多问题和推动科学发展方面起到了重要作用,但它仍然存在一些局限性,无法完全处理人类的认知与智能。因此,我们需要综合运用多种学科的知识和方法,以更全面、综合的方式来理解和处理人类的认知与智能。