有约束线性最小二乘

其标准形式为：
$$\underset{x}{\min }\frac{1}{2}{\Vert Cx-d\Vert }_2^2$$
约束条件为：
$$\begin{array}{rl}A\cdot x& \le b\\ A_{eq}\cdot x& =b_{eq}\\ lb\le & x\le ub\end{array}$$
matlab 使用 lsqlin 求解该类型问题，调用格式如下
x = lsqlin(C, d, A, B, Aeq, Beq, lb, ub, x0)
[x, resnorm, residual] = lsqlin(C, d, A, B, Aeq, Beq, lb, ub, x0)
没有的约束设置为 [] 就行，x0 是初始解向量，比如说你知道解大概是多少，设了可以避免陷入局部最优，减少优化时间等，没有可以不加或者设置为 []。resnorm就是${\Vert Cx-d\Vert }_2^2$，residual就是$Cx-d$.
假设已知有一个函数为：
$$y=a_0\ast x+a_1\times \sqrt{x}-a_2\times x^{0.8}+a_3+noise$$
其中 $a_0=1,a_1=2,a_2=-3,a_3=4$，如何用有噪声的数据将参数求出来。
噪声数据如图

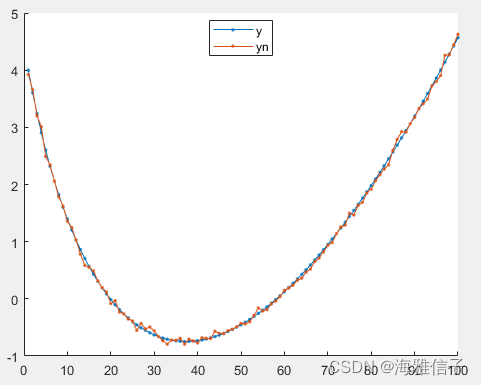
仿真如下：

% created by hyacinth on 2024/1/8
clc
clear
close all

%%
x1 = 1:100;
x2 = x1.^0.5;
x3 = x1.^0.8;
x4 = ones(size(x1));

y = x1 + 2*x2 - 3*x3 + 4*x4;
yn = y + 0.05*randn(size(x1));

C = [x1',x2',x3',x4'];
d = yn';
theta = lsqlin(C,d);

因为题目是我瞎编的，没加什么约束，实际中有约束加上去就行了，比如说约束上下界 $lb=-10,ub=10$。

lb = -10*ones(1,4);
ub = 10*ones(1,4);
theta = lsqlin(C,d,[],[],[],[],lb,ub);

这样设置就行了，最后求出来的系数为：
$$theta=[1.0106;2.0880;-3.0468;3.9113]$$

非线性曲线拟合

跟上面很像，比如说知道输入输出函数关系，但是不知道系数向量，就可以进行曲线拟合。
$$\underset{x}{\min }\frac{1}{2}{\Vert F(x,x_{data})-y_{data}\Vert }_2^2=\frac{1}{2}\sum _i{\left(F(x,x_{dat{a}_i})-y_{dat{a}_i}\right)}^2$$
matlab 调用函数如下：
[x, resnorm] = lsqcurvefit(fun, x0, xdata, ydata,lb,ub)
以x0作为初始解，求取合适的系数，使得非线性函数fun满足最佳拟合。lb，ub是系数的边界约束条件，没有就不加。resnorm就是$\frac{1}{2}{\Vert F(x,x_{data})-y_{data}\Vert }_2^2$的值。
还是一样，比如说要拟合曲线
$$y=a_0\ast x+a_1\times \sqrt{x}-a_2\times x^{0.8}+a_3$$
先建立函数

function y = myfun(a,xdata)
y = a(1)*xdata + a(2)*sqrt(xdata) + a(3)*xdata.^0.8 + a(4)*1;

拟合

% created by hyacinth on 2024/1/8
clc
clear
close all

%%
x1 = 1:100;
x2 = x1.^0.5;
x3 = x1.^0.8;
x4 = ones(size(x1));

y = x1 + 2*x2 - 3*x3 + 4*x4;
yn = y + 0.05*randn(size(x1));

x0 = [1,1,1,1];
a = lsqcurvefit(@myfun,x0,x1,yn);

最后的解为
$$a=[0.9969,1.9763,-2.9865,4.0131]$$

非负线性最小二乘

$$\underset{x}{\min }\frac{1}{2}{\Vert Cx-d\Vert }_2^2$$
约束条件为：
$$x\ge 0$$
matlab 调用函数如下：
x = lsqnonneg(C, d)
[x, resnorm, residual] = lsqnonneg(C, d)
其中resnorm就是${\Vert Cx-d\Vert }_2^2$，residual就是$Cx-d$.
比如说将上面的函数改为
$$y=a_0\ast x+a_1\times \sqrt{x}+a_2\times x^{0.8}+a_3+noise$$
其中 $a_0=1,a_1=2,a_2=3,a_3=4$，使用有噪声的数据求参数。

% created by hyacinth on 2024/1/8
clc
clear
close all

%%
x1 = 1:100;
x2 = x1.^0.5;
x3 = x1.^0.8;
x4 = ones(size(x1));

y = x1 + 2*x2 + 3*x3 + 4*x4;
yn = y + 0.05*randn(size(x1));

C = [x1',x2',x3',x4'];
d = yn';
theta = lsqnonneg(C,d);

最后的结果为：
$$theta=[0.9918;1.9662;3.0294;3.9876]$$