本文仅供学习使用
本文参考：
B站：DR_CAN

---

1. 三角函数的正交性

三角函数系 ： 集合 { sin ⁡ n x , cos ⁡ n x } n = 0 , 1 , 2 , ⋯ \left\{ \sin nx,\cos nx \right\} n=0,1,2,\cdots {sinnx,cosnx}n=0,1,2,⋯
正交：
$$\begin{gathered} {\int }_{-\pi }^{\pi }\sin nx\sin mx\mathrm{d}x=0,n\ne m \\ {\int }_{-\pi }^{\pi }\sin nx\cos mx\mathrm{d}x=0,n\ne m \\ {\int }_{-\pi }^{\pi }\cos nx\sin mx\mathrm{d}x=0,n\ne m \end{gathered}$$

积化和差：$\Rightarrow {\int }_{-\pi }^{\pi }\frac{1}{2}\left[\cos \left(n-m\right)x+\cos \left(n+m\right)x\right]\mathrm{d}x=\frac{1}{2}\frac{1}{\left(n-m\right)}\sin \left(n-m\right)x{\mid }_{-\pi }^{\pi }+\frac{1}{2}\frac{1}{\left(n+m\right)}\sin \left(n+m\right)x{\mid }_{-\pi }^{\pi }$
$${\int }_{-\pi }^{\pi }\cos mx\cos mx\mathrm{d}x=\pi$$

2. 周期为$2\pi$的函数展开为傅里叶级数

$T=2\pi :f\left(x\right)=f\left(x+2\pi \right)$

$$f\left(x\right)=\sum _{n=0}^{\infty }{a}_{\mathrm{n}}\cos nx+\sum _{n=0}^{\infty }{b}_{\mathrm{n}}\sin nx=a_0\cos ox+\sum _{n=1}^{\infty }{a}_{\mathrm{n}}\cos nx+b_0\sin 0x+\sum _{n=1}^{\infty }{b}_{\mathrm{n}}\sin nx=a_0+\sum _{n=1}^{\infty }{a}_{\mathrm{n}}\cos nx+\sum _{n=1}^{\infty }{b}_{\mathrm{n}}\sin nx$$

1. 找$a_0$:
   $$\begin{gathered} {\int }_{-\pi }^{\pi }f\left(x\right)\mathrm{d}x={\int }_{-\pi }^{\pi }{a}_0\mathrm{d}x+{\int }_{-\pi }^{\pi }1\cdot \sum _{n=1}^{\infty }{a}_{\mathrm{n}}\cos nx\mathrm{d}x+{\int }_{-\pi }^{\pi }1\cdot \sum _{n=1}^{\infty }{b}_{\mathrm{n}}\sin nx\mathrm{d}x \\ =a_0{\int }_{-\pi }^{\pi }\mathrm{d}x+0+0=a_0\cdot 2\pi \end{gathered}$$
   $$\Rightarrow a_0=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\mathrm{d}x$$
2. 找$a_n$:
   $${\int }_{-\pi }^{\pi }f\left(x\right)\cos mx\mathrm{d}x={\int }_{-\pi }^{\pi }{a}_0\cos mx\cdot 1\mathrm{d}x+{\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }{a}_{\mathrm{n}}\cos nx\cos mx\mathrm{d}x+{\int }_{-\pi }^{\pi }\sum _{n=1}^{\infty }{b}_{\mathrm{n}}\sin nx\cos mx\mathrm{d}x={\int }_{-\pi }^{\pi }{a}_{\mathrm{n}}\cos nx\cos nx\mathrm{d}x=a_{\mathrm{n}}\pi$$
   $$\Rightarrow a_{\mathrm{n}}=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\cos nx\mathrm{d}x$$
3. 找$b_n$:
   $${\int }_{-\pi }^{\pi }f\left(x\right)\sin .mx\mathrm{d}x\Rightarrow b_{\mathrm{n}}=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\sin nx\mathrm{d}x$$

$$\Rightarrow f\left(x\right)=f\left(x+2\pi \right),T=2\pi \{\begin{array}{l}f\left(x\right)=\frac{a_0}{2}+{\sum }_{n=0}^{\infty }{a}_{\mathrm{n}}\cos nx+{\sum }_{n=0}^{\infty }{b}_{\mathrm{n}}\sin nx\\ a_0=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\mathrm{d}x\\ a_{\mathrm{n}}=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\cos nx\mathrm{d}x\\ b_{\mathrm{n}}=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\sin nx\mathrm{d}x\end{array}$$

3. 周期为$2L$的函数展开

$f\left(t\right)=f\left(t+2L\right)$ , 换元：$x=\frac{\pi }{L}t,t=\frac{L}{\pi }x$
$f\left(t\right)=f\left(\frac{L}{\pi }x\right)=g\left(x\right),g\left(x+2\pi \right)=f\left(\frac{L}{\pi }\left(x+2\pi \right)\right)=f\left(\frac{L}{\pi }x+2L\right)=f\left(\frac{L}{\pi }x\right)=g\left(x\right)$

$$\begin{gathered} g\left(x\right)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left[a_{\mathrm{n}}\cos nx+b_{\mathrm{n}}\sin nx\right] \\ {a}_0=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\mathrm{d}x,a_{\mathrm{n}}=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\cos nx\mathrm{d}x,b_{\mathrm{n}}=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\sin nx\mathrm{d}x \end{gathered}$$

$$\begin{gathered} \to x=\frac{\pi }{L}t\Rightarrow \cos nx=\cos \frac{n\pi }{L}t,\sin nx=\sin \frac{n\pi }{L}t,g\left(x\right)=f\left(t\right) \\ {\int }_{-\pi }^{\pi }\mathrm{d}x={\int }_{-\pi }^{\pi }\mathrm{d}\frac{\pi }{L}t\Rightarrow \frac{1}{\pi }{\int }_{-\pi }^{\pi }\mathrm{d}x=\frac{1}{L}{\int }_{-L}^L\mathrm{d}t \end{gathered}$$

$$\Rightarrow f\left(t\right)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left[a_{\mathrm{n}}\cos \frac{n\pi }{L}t+b_{\mathrm{n}}\sin \frac{n\pi }{L}t\right],a_0=\frac{1}{L}{\int }_{-L}^{L}f\left(t\right)\mathrm{d}t,a_{\mathrm{n}}=\frac{1}{L}{\int }_{-L}^{L}f\left(t\right)\cos \frac{n\pi }{L}t\mathrm{d}t,b_{\mathrm{n}}=\frac{1}{L}{\int }_{-L}^{L}f\left(t\right)\sin \frac{n\pi }{L}t\mathrm{d}t$$

4. 傅里叶级数的复数形式

$$\begin{gathered} f\left(t\right)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left[a_{\mathrm{n}}\frac{1}{2}\left(e^{inwt}+e^{-inwt}\right)-b_{\mathrm{n}}\frac{1}{2}\left(e^{inwt}-e^{-inwt}\right)\right]=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left[\frac{a_{\mathrm{n}}-i{b}_{\mathrm{n}}}{2}{e}^{inwt}+\frac{a_{\mathrm{n}}+i{b}_{\mathrm{n}}}{2}{e}^{-inwt}\right] \\ =\sum _{n=0}^0\frac{a_0}{2}{e}^{inwt}+\sum _{n=1}^{\infty }\frac{a_{\mathrm{n}}-i{b}_{\mathrm{n}}}{2}{e}^{inwt}+\sum _{n=-\infty }^{-1}\frac{a_{\mathrm{n}}+i{b}_{\mathrm{n}}}{2}{e}^{inwt} \\ =\sum _{n=-\infty }^{\infty }{C}_{\mathrm{n}}{e}^{inwt},C_{\mathrm{n}}=\{\begin{array}{l}\frac{a_0}{2}n=0\\ \frac{a_{\mathrm{n}}-i{b}_{\mathrm{n}}}{2}n=1,2,3,\cdots \\ \frac{a_{\mathrm{n}}+i{b}_{\mathrm{n}}}{2}n=-1,-2,-3,\cdots \end{array}\begin{array}{c}\to \frac{1}{T}{\int }_0^{T}f\left(t\right)\mathrm{d}t\\ \to \frac{1}{T}{\int }_0^{T}f\left(t\right)\left(\cos nwt-i\sin nwt\right)\mathrm{d}t=\frac{1}{T}{\int }_0^{T}f\left(t\right)\left(\cos \left(-nwt\right)+i\sin \left(-nwt\right)\right)\mathrm{d}t=\frac{1}{T}{\int }_0^{T}f\left(t\right)e^{-inwt}\mathrm{d}t\\ \to \frac{1}{T}{\int }_0^{T}f\left(t\right)e^{-inwt}\mathrm{d}t\end{array} \\ \Rightarrow f\left(t\right)=\sum _{-\infty }^{\infty }{C}_{\mathrm{n}}{e}^{inwt},C_{\mathrm{n}}=\frac{1}{T}{\int }_0^{T}f\left(t\right)e^{-inwt}\mathrm{d}t \end{gathered}$$

• Euler’s Formula

5. 从傅里叶级数推导傅里叶变换FT

$f_{\mathrm{T}}\left(t\right)=f\left(t+T\right)$
$f_{\mathrm{T}}\left(t\right)={\sum }_{-\infty }^{\infty }{C}_{\mathrm{n}}{e}^{in{w}_{0}t}$, 基频率：$w_0=\frac{2\pi }{T}$, 定义函数: $C_{\mathrm{n}}=\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{f}_{\mathrm{T}}\left(t\right)e^{-inwt}\mathrm{d}t$

非周期，一般形式：$T\to \infty$
$$\underset{T\to \infty }{\lim }{f}_{\mathrm{T}}\left(t\right)=f\left(t\right),\Delta w=\left(n+1\right)w_0-n{w}_0=w_0=\frac{2\pi }{T}T\nearrow \Delta w\searrow$$

$$\begin{gathered} f_{\mathrm{T}}\left(t\right)=\sum _{-\infty }^{\infty }\left(\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{f}_{\mathrm{T}}\left(t\right)e^{-in{w}_{0}t}\mathrm{d}t\right)e^{in{w}_{0}t},\frac{1}{T}=\frac{\Delta w}{2\pi } \\ \Rightarrow f_{\mathrm{T}}\left(t\right)=\sum _{-\infty }^{\infty }\left(\frac{\Delta w}{2\pi }{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{f}_{\mathrm{T}}\left(t\right)e^{-in{w}_{0}t}\mathrm{d}t\right)e^{in{w}_{0}t},T\to \infty :\{\begin{array}{l}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}\mathrm{d}t\to {\int }_{-\infty }^{\infty }\mathrm{d}t\\ n{w}_0\to w\\ {\sum }_{-\infty }^{\infty }\Delta w\to {\int }_{-\infty }^{\infty }\mathrm{d}w\end{array} \\ \Rightarrow f\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\left({\int }_{-\infty }^{\infty }f\left(t\right)e^{-iwt}\mathrm{d}t\right)e^{iwt}\mathrm{d}w,{\int }_{-\infty }^{\infty }f\left(t\right)e^{-iwt}\mathrm{d}t=F\left(w\right) \\ \Rightarrow f\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F\left(w\right)e^{iwt}\mathrm{d}w \end{gathered}$$

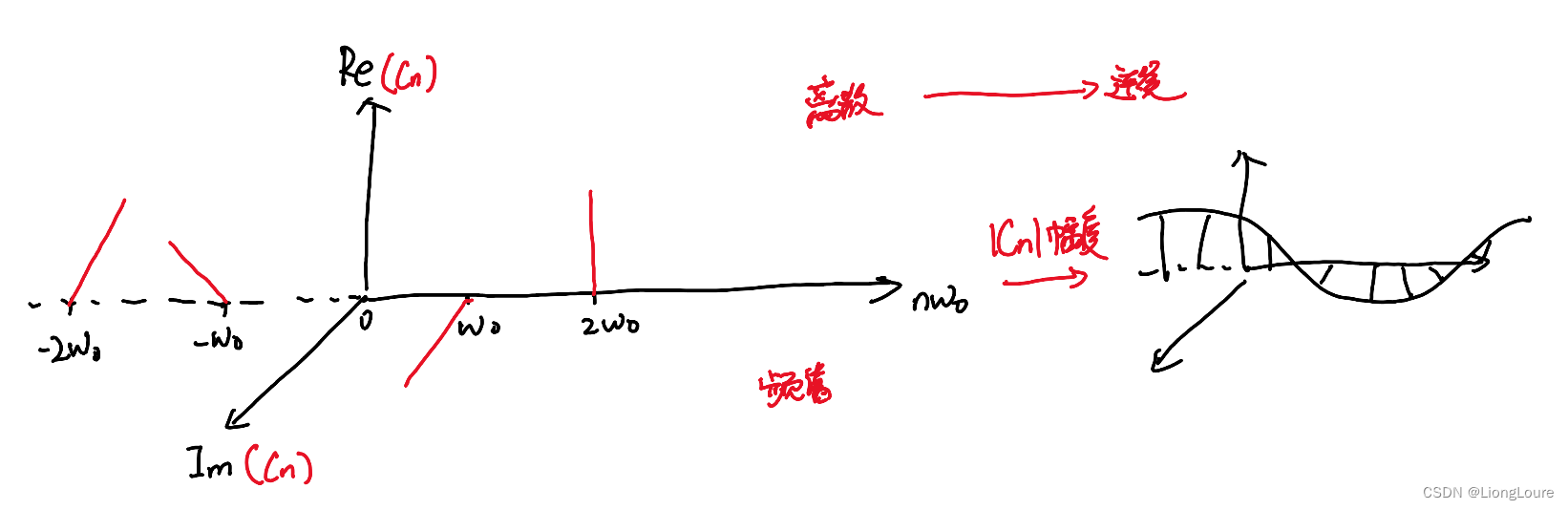
$F\left(w\right)={\int }_{-\infty }^{\infty }f\left(t\right)e^{-iwt}\mathrm{d}t$ : FT 傅里叶变换

$f\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F\left(w\right)e^{iwt}\mathrm{d}w$ : 逆变换

6. 总结

三角函数的正交性：
$\left[0,1,\sin x,\cos x,\sin 2x,\cos 2x,\cdots ,\sin nx,\cos nx\right],n=0,1,2,\cdots$
$$\begin{gathered} {\int }_{-\pi }^{\pi }\sin nx\sin mx\mathrm{d}x=0,n\ne m \\ {\int }_{-\pi }^{\pi }\sin nx\sin mx\mathrm{d}x=0,n\ne m \\ {\int }_{-\pi }^{\pi }\sin nx\cos mx\mathrm{d}x=0,n\ne m \end{gathered}$$

周期$2\pi$ :
$f\left(x\right)=f\left(x+2\pi \right)$
$$f\left(x\right)=\sum _{n=0}^{\infty }{a}_{\mathrm{n}}\cos nx+\sum _{n=0}^{\infty }{b}_{\mathrm{n}}\sin nx\leftarrow f\left(x\right)=\frac{a_0}{2}+\sum _{n=0}^{\infty }{a}_{\mathrm{n}}\cos nx+\sum _{n=0}^{\infty }{b}_{\mathrm{n}}\sin nx$$
$a_0=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\mathrm{d}x,a_{\mathrm{n}}=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\cos nx\mathrm{d}x,b_{\mathrm{n}}=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\sin nx\mathrm{d}x$

周期$2L$ :
$T=2L,f\left(t\right)=f\left(t+2L\right),x=\frac{\pi }{L}t$
$$f\left(t\right)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left[a_{\mathrm{n}}\cos \frac{n\pi }{L}t+b_{\mathrm{n}}\sin \frac{n\pi }{L}t\right]$$
$a_0=\frac{1}{L}{\int }_{-L}^{L}f\left(t\right)\mathrm{d}t,a_{\mathrm{n}}=\frac{1}{L}{\int }_{-L}^{L}f\left(t\right)\cos \frac{n\pi }{L}t\mathrm{d}t,b_{\mathrm{n}}=\frac{1}{L}{\int }_{-L}^{L}f\left(t\right)\sin \frac{n\pi }{L}t\mathrm{d}t$

复指数：
$$f\left(t\right)=\sum _{-\infty }^{\infty }{C}_{\mathrm{n}}{e}^{in{w}_{0}t},w_0=\frac{2\pi }{T},C_{\mathrm{n}}=\frac{1}{T}{\int }_0^{T}f\left(t\right)e^{-in{w}_{0}t}\mathrm{d}t$$

FT ：
$f\left(t\right)=f\left(t+T\right),T\to \infty$ , $f\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\left({\int }_{-\infty }^{\infty }f\left(t\right)e^{-iwt}\mathrm{d}t\right)e^{iwt}\mathrm{d}w$
$$\begin{array}{c}FT\to F\left(w\right)={\int }_{-\infty }^{\infty }f\left(t\right)e^{-iwt}\mathrm{d}t\\ IFT\to \left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F\left(w\right)e^{iwt}\mathrm{d}w\end{array}$$
Laplace : $F\left(s\right):{\int }_{-\infty }^{\infty }f\left(t\right)e^{-st}\mathrm{d}t$