回溯算法
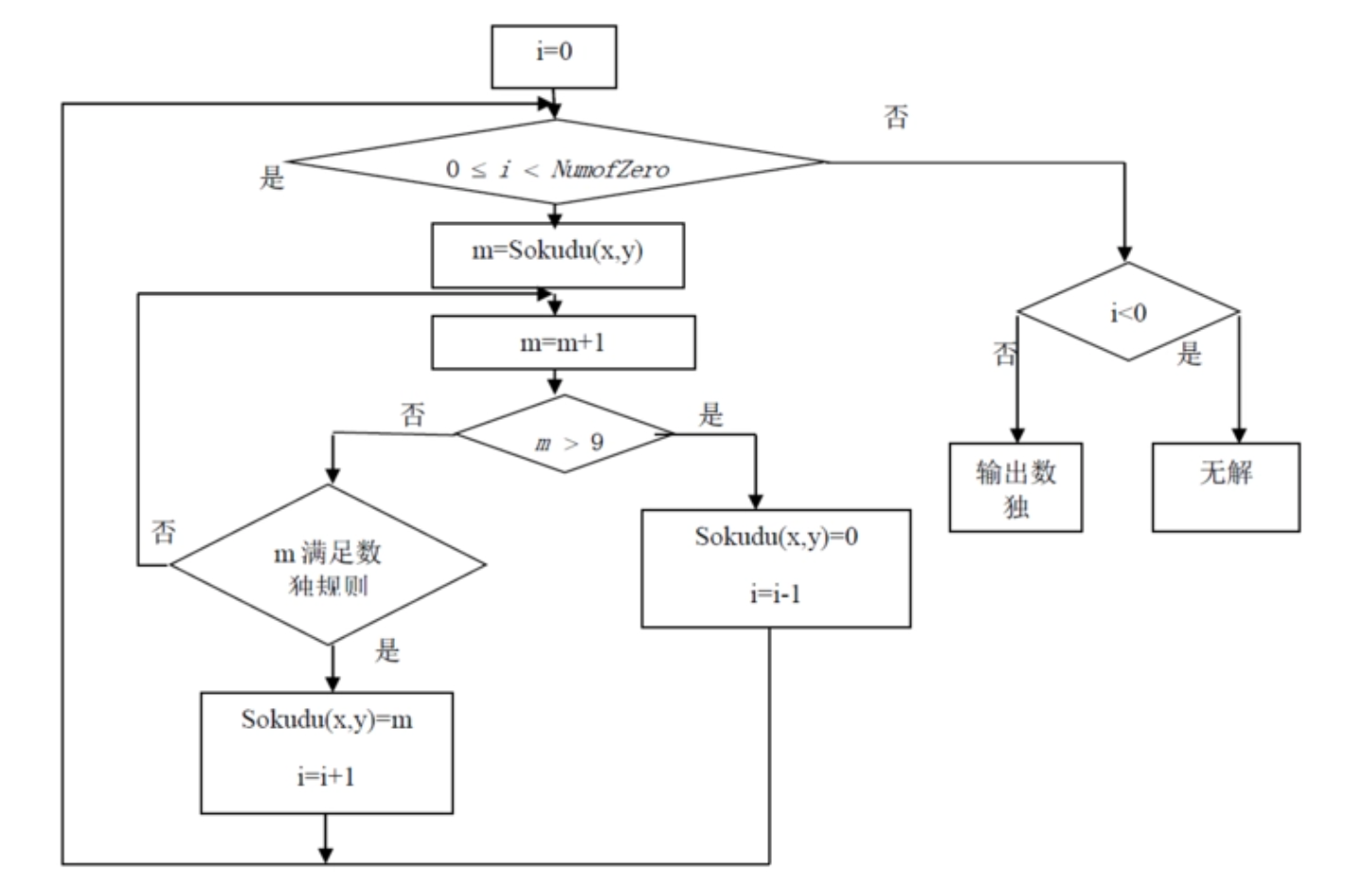
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
最短路径算法
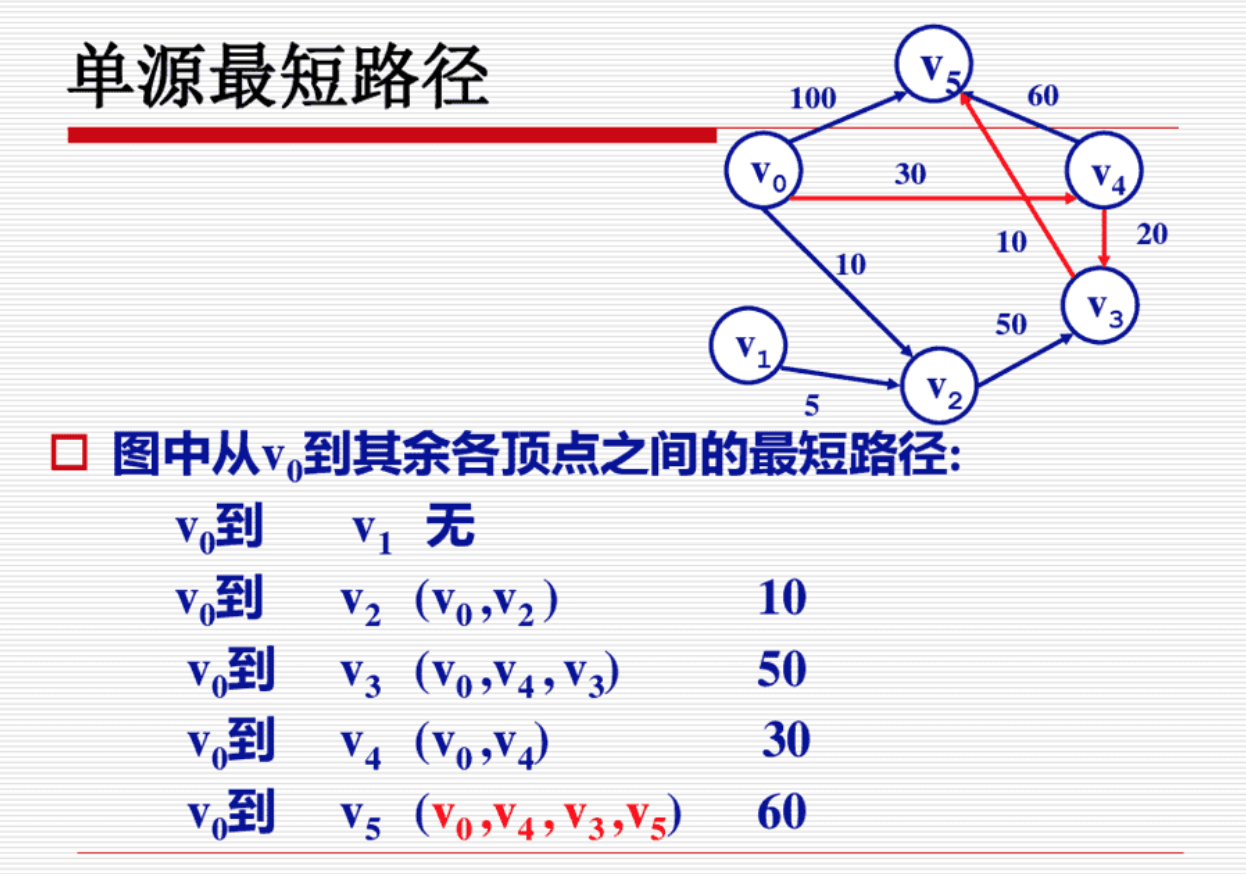
从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径叫做最短路径。解决最短路的问题有以下算法,Dijkstra 算法,Bellman-Ford 算法,Floyd 算法和 SPFA算法等。
最小生成树算法
现在假设有一个很实际的问题:我们要在 n 个城市中建立一个通信网络,则连通这 n 个城市需要布置 n-1 一条通信线路,这个时候我们需要考虑如何在成本最低的情况下建立这个通信网?
于是我们就可以引入连通图来解决我们遇到的问题,n 个城市就是图上的 n 个顶点,然后,边表示两个城市的通信线路,每条边上的权重就是我们搭建这条线路所需要的成本,所以现在我们有 n 个顶点的连通网可以建立不同的生成树,每一颗生成树都可以作为一个通信网,当我们构造这个连通网所花的成本最小时,搭建该连通网的生成树,就称为最小生成树。
构造最小生成树有很多算法,但是他们都是利用了最小生成树的同一种性质:MST 性质(假设N=(V,{E})是一个连通网,U 是顶点集 V 的一个非空子集,如果(u,v)是一条具有最小权值的边,其中 u 属于 U,v 属于 V-U,则必定存在一颗包含边(u,v)的最小生成树),下面就介绍两种使用 MST 性质生成最小生成树的算法:普里姆算法和克鲁斯卡尔算法。