题目

给定一个非空的正整数数组和一个目标值S，如果为每个数字添加“+”或“-”运算符，请计算有多少种方法可以使这些整数的计算结果为S。例如，如果输入数组[2，2，2]并且S等于2，有3种添加“+”或“-”的方法使结果为2，它们分别是2+2-2=2、2-2+2=2及-2+2+2=2。

分析

在分析解决这个问题之前，需要先做数学运算。首先数组元素都是正整数，为输入的数组中的有些数字添加“+”，有些数字添加“-”。如果所有添加“+”的数字之和为p，所有添加“-”的数字之和为q，按照题目的要求，p-q=S。如果累加数字中的所有数字，就能得到整个数组的数字之和，记为sum，即p+q=sum。将这两个等式的左右两边分别相加，就可以得到2p=S+sum，即p=（S+sum）/2。
上面的等式表明，如果能够找出数组中和为（S+sum）/2的数字，并给它们添加“+”，然后给其他数字添加“-”，那么最终的计算结果就是S。因此，这个题目等价于计算从数组中选出和为（S+sum）/2的数字的方法的数目。这是和前面的面试题非常类似的题目，是一个典型的0-1背包问题，可以用动态规划解决。
可以用函数f（i，j）表示在数组的前i个数字（即nums[0…i-1]）中选出若干数字使和等于j的方法的数目。如果数组的长度为n，目标和为t，那么f（n，t）就是整个问题的解。

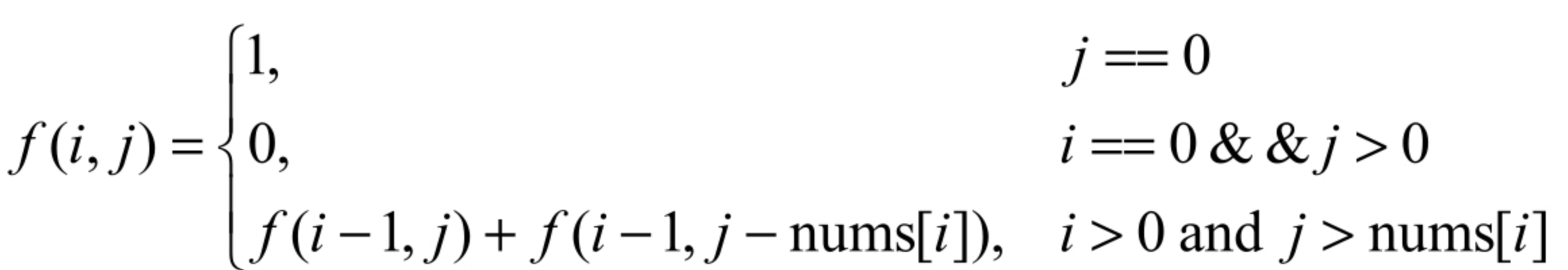
解

public class Test {
    public static void main(String[] args) {
        int[] nums = {2, 2, 2};
        int result = findTargetSumWays(nums, 2);
        System.out.println(result);
    }

    public static int findTargetSumWays(int[] nums, int S) {
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }

        if ((sum + S) % 2 == 1 || sum < S) {
            return 0;
        }

        return subsetSum(nums, (sum + S) / 2);
    }

    private static int subsetSum(int[] nums, int target) {
        int[][] dp = new int[nums.length + 1][target + 1];
        for (int i = 0; i < nums.length; i++) {
            dp[i][0] = 1;
        }

        for (int i = 1; i <= nums.length; i++) {
            for (int j = 1; j <= target; j++) {
                dp[i][j] += dp[i - 1][j];// 不选择元素nums[i-1];
                if (j >= nums[i - 1]) {
                    dp[i][j] += dp[i - 1][j - nums[i - 1]]; // 选择元素nums[i-1];
                }
            }
        }

        return dp[nums.length][target];
    }

}