【数据结构】栈的基本知识详解

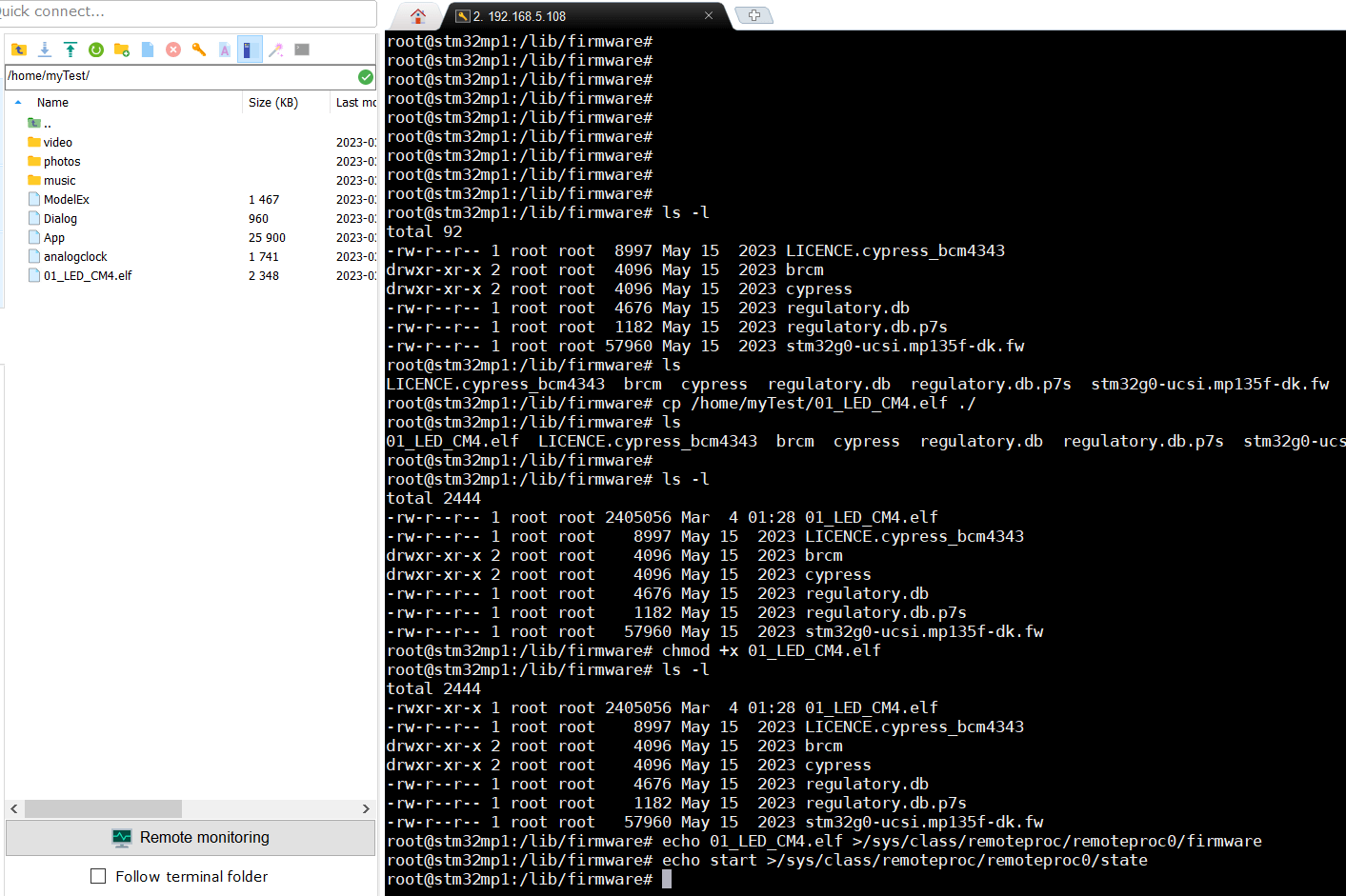
栈的基本概念与基本操作

导言
一、栈的基本概念
- 1.1 栈的定义
- 1.2 栈的重要术语
- 1.3 栈的数学性质
二、栈的基本操作
结语

导言

大家好，很高兴又和大家见面了！！！
今天开始，咱们将正式进入【数据结构】第三章的内容介绍。在第三章的内容中，我们需要掌握栈和队列的操作及其特征，以及数组与特殊矩阵的压缩存储等知识点。为了更好的掌握这些知识点，我们将对这些知识点进行一一介绍。
今天要介绍的是咱们的第一位新朋友——栈。我们在今天的篇章中需要搞清楚以下几个问题：

什么是栈？
栈有哪些重要术语？
栈的操作特性是什么？
栈有哪些基本操作？

下面我们就开始今天的内容吧！

一、栈的基本概念

1.1 栈的定义

栈（Stack）是只允许在一端进行插入或者删除操作的线性表。

在前面的学习中，我们知道了线性表就是具有相同数据类型的n(n>=0)个数据元素的有限序列。从栈的定义中我们可以看到，栈也是一个线性表，也就是说存放在栈中的数据元素是有限的，且数据元素的数据类型相同。我们需要注意的是栈的定义中强调了一个点——只允许在一端进行插入或者删除操作。

为什么要强调只允许在一端进行插入或者删除呢？下面我们来回忆一下线性表。

在顺序表中，我们在进行插入或删除操作时可以通过元素的位序进行随机存取，从而完成插入或者删除的操作；
在链表中，我们同样可以通过元素对应的位序来完成插入或者删除操作；
也就是说不管是顺序表还是链表，在进行插入或者删除操作时我们只需要得到数据元素对应的位序就能实现，因此，这两种线性表都是可以在表中的任意位置进行插入或者删除操作的。

在结合这里的只允许在一端，我们就能得到结论，对于栈这种线性表它在进行插入或者删除操作时是有局限性的。

1.2 栈的重要术语

栈顶（Top）——线性表允许进行插入删除的一端；
栈底（Bottom）——线性表不允许进行插入删除的一端；
空栈——不含任何元素的空表。
接下来我们根据图像来更进一步理解这些术语：
栈的重要术语

我们可以把栈想象成一个水杯，我们在倒水时只能从杯口往杯里加水，喝水时只能从杯口将杯中的水倒出来；杯子的杯底是固定的，我们不能通过从杯底进行加水和倒水；当杯子中没有任何东西时，这个杯子为空杯。
因此，水杯的杯口就是栈的栈顶；水杯的杯底就是栈的栈底；水杯中没有任何东西时，对应的就是栈中没有任何数据元素，此时的空杯对应的栈为空栈。

下面我们假设某个栈S中有 $a_1,a_2,a_3,a_4,a_5$ 这五个元素，如下图所示：
栈的重要术语2
由于只能从栈顶进行插入和删除操作，因此我们在将这个五个元素依次放入栈中时，它们放入的顺序应该是：
$a_1->a_2->a_3->a_4->a_5$ ，而它们的存放从上到下依次是： $a_5->a_4->a_3->a_2->a_1$ 。在这个栈中 $a_1$ 是离栈底最近的元素，因此它也被称为栈底元素，而 $a_5$ 是离栈顶最近的元素，因此它也被称为栈顶元素。如果我们需要删除这些元素时，我们也应该按照它们的存放顺序进行删除也就是： $a_5->a_4->a_3->a_2->a_1$ 。

由此可见，对于栈这种线性表而言他的操作特性可以概括为——后进先出（Last In First Out，LIFO）。

Tips：

我们在介绍【函数栈帧的创建与销毁】时，就有提到过函数的栈帧空间。在创建一个新的函数栈帧时，就有进行压栈和出栈等操作，进行压栈和出栈时就是从栈顶实现的。
我们在存放数据时，会根据数据存放的空间的起始地址来标记该元素的所在位置，如果将对应的空间想象成栈的话，那指向该空间的指针，指向的就是这个空间的栈顶。

1.3 栈的数学性质

由于栈的操作性质，那我们在对其进行入栈和出栈操作时就可能会出现以下的几种情况：

按元素顺序进行入栈，全部入栈后再依次出栈；
按元素顺序进行入栈，入栈的过程中穿插出栈；

对于第一种情况我们可以很好的理解它的元素出栈顺序——与入栈顺序相反；
但是在第二种情况下，如果有n个元素进行入栈与出栈操作，出栈元素不同的排列个数为 $1/(n+1)C^{n}_{2n}$ 。这个公式被称为卡特兰数（Catalan），这个公式也是栈的数学性质。

二、栈的基本操作

在介绍线性表时，我们有介绍过线性表的基本操作概括一下就是——创建、销毁、增删改查。当然我们在修改元素前也是需要先查找到对应元素才行。对于栈这种线性表而言，我们可以对其进行的基本操作同样可以总结为以下几点：

1.创建销毁

InitStack(&S)：初始化一个空栈S；
DestroyStack(&S)：销毁栈，并释放栈S占用的存储空间；

对于栈的创建与销毁操作，它和线性表一样都是对整个对象进行修改，所以这里需要使用引用符号，通过C语言实现的话就是需要借助指针，如下所示：

//初始化
bool InitStack(StackType* S);
//销毁
bool DestroyStack(StackType* S);
//StackType——栈的数据类型
//StackType*——指针数据类型
void test() {
	StackType S;//定义数据类型为StackType类型的栈S
	InitStack(&S);//对栈进行初始化
	DestroyStack(&S);//销毁栈
}

对于栈的数据类型今天我们就不再展开，在下一篇栈的基本操作的C语言实现中，我们会再详细介绍；

增加删除

Push(&S,x)：进栈，若栈S未满，则将x加入使之称为新的栈顶；
Pop(&S,&x)：出栈，若栈S非空，则弹出栈顶元素，并用x返回；

对于栈的增加与删除操作，可以看到都是对栈顶元素进行的，但是有一点不同的是，我们在进行增加即进栈操作时，并未对数据x进行引用操作，但是在出栈时需要对x进行引用。
这是因为我们在进栈时是对明确的元素进行进栈操作，这时我们需要修改的只有栈空间，但是在出栈操作时，我可能并不知道此时的栈顶元素存储的是什么内容，我只需要删除栈顶元素，所以我需要将删除的元素给带回到主函数中来告诉大家我们现在删除的是什么元素，因此需要对x进行引用，通过C语言来实现的话则是：

//进栈
bool Push(StackType* S, ElemType x);
//出栈
bool Pop(StackType* S, ElemType* x);
//StackType——栈的数据类型
//StackType*——指针数据类型
//ElemType——数据元素的数据类型
//ElemType*——指针数据类型
void test() {
	StackType S;//定义数据类型为StackType类型的栈S
	ElemType x = 0;
	Push(&S, x);//进栈
	Pop(&S, &x);//出栈
}

与线性表一样，在具体的实现中我们对于进栈和出栈的函数返回类型可以根据要求进行变化，不一定是布尔类型；

查找

GetTop(S,&x)：读栈顶元素，若栈S非空，则用x返回栈顶元素；

在对栈进行查找操作时，我们查找的是栈顶元素，并且需要将查找到的栈顶元素进行带回，因此这里需要对x进行引用，通过C语言实现的话则是：

//查找
bool GetTop(StackType S, ElemType* x);
//StackType——栈的数据类型
//ElemType——数据元素的数据类型
//ElemType*——指针数据类型
void test() {
	StackType S;//定义数据类型为StackType类型的栈S
	ElemType x = 0;
	GetTop(S, &x);//查找栈顶元素
}

具体的返回类型我们也可以根据需求进行修改，因为这里是通过传址的方式进行传参，所以只要在函数中对x存储的数值有进行修改，那回到主函数后实参也会跟着被修改；

4.其它

StackEmpty(S)：判断一个栈是否为空，若栈S为空则返回true，否则返回false；

对于判空操作而言，就是简单的判断一下栈中有没有元素，因此并未对栈的内容有任何更改，所以这里我们不需要使用引用操作，用C语言表示则是：

//判空
bool StackEmpty(StackType S);
//StackType——栈的数据类型
void test() {
	StackType S;//定义数据类型为StackType类型的栈S
	StackEmpty(S);//判空
}

在不需要对实参进行修改的函数调用中，我们只需要通过传值传参即可。

以上就是栈的基本操作的C语言格式，对于具体的参数类型、函数的返回类型以及函数的具体实现，我们会在后面的篇章中详细介绍，大家记得关注哦！

结语

今天的内容比较简单在今天的内容中，我们主要介绍了在导言部分提出的几个问题：

什么是栈？
栈（Stack）是只允许在一端进行插入或者删除操作的线性表

栈有哪些重要术语？
栈顶、栈底、空栈、栈顶元素、栈底元素

栈的操作特性是什么？
后进先出——Last In First Out，LIFO

栈有哪些基本操作？
创建销毁、增加删除、查找、判空

咱们还简单介绍了一下栈的数学性质——卡特兰数（Catalan），在后面的篇章中我会进行详细的介绍，大家记得关注哦！

今天的内容到这里就结束了，希望这篇内容能帮助大家更好的理解栈的基础知识点，在接下来的内容中咱们将继续介绍如何通过C语言实现栈的基本操作。最后感谢大家翻阅，咱们下一篇再见！！！