提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
前言
一、选择排序
1、基本思想
2、直接选择排序
3、选择排序的代码实现
二、堆排序
2.1算法讲解
2.2堆排序的代码实现
总结
前言
世上有两种耀眼的光芒,一种是正在升起的太阳,一种是正在努力学习编程的你!一个爱学编程的人。各位看官,我衷心的希望这篇博客能对你们有所帮助,同时也希望各位看官能对我的文章给与点评,希望我们能够携手共同促进进步,在编程的道路上越走越远!
提示:以下是本篇文章正文内容,下面案例可供参考
一、选择排序
1.1基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
1.2直接选择排序
1、在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素。
2、若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)。3、元素交换在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素。
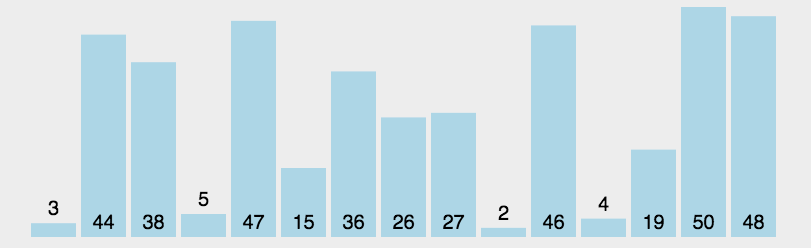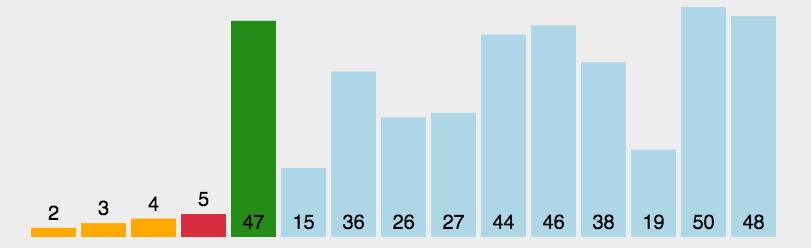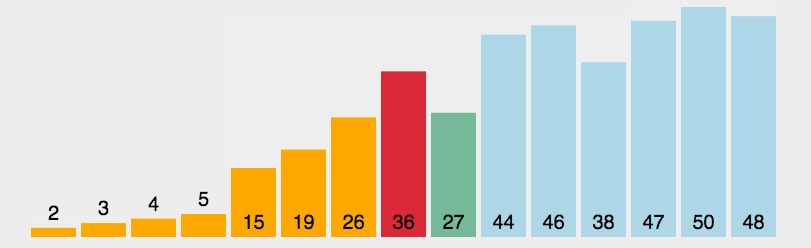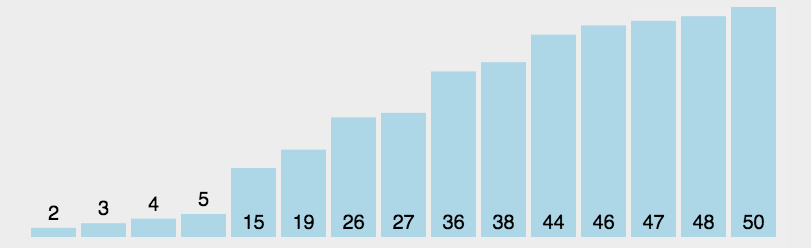
直接选择排序的特性总结:
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
1.3选择排序的代码实现
Sort.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <time.h>
//打印数组
void PrintArray(int* a, int n);
//选择排序
void SelectSort(int* a, int n);Sort.c//打印数组
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
//交换
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//选择排序O(N^2)
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin + 1; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[begin], &a[mini]);
//如果最大的值的位置刚好在最左边的位置,最小值的位置跑到最左边时,最大值的位置也要变
if (maxi == begin)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
begin++;
end--;
}
}
test.c#define _CRT_SECURE_NO_WARNINGS 1
#include"Sort.h"
void TestSelectSort()
{
//int a[] = { 3,2,6,8,4,6,0,9,5,1,7 };
int a[] = { 13,2,6,8,4,6,0,9,5,1,7 };
SelectSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
int main()
{
TestSelectSort();
return 0;
}
二、堆排序
2.1算法讲解
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
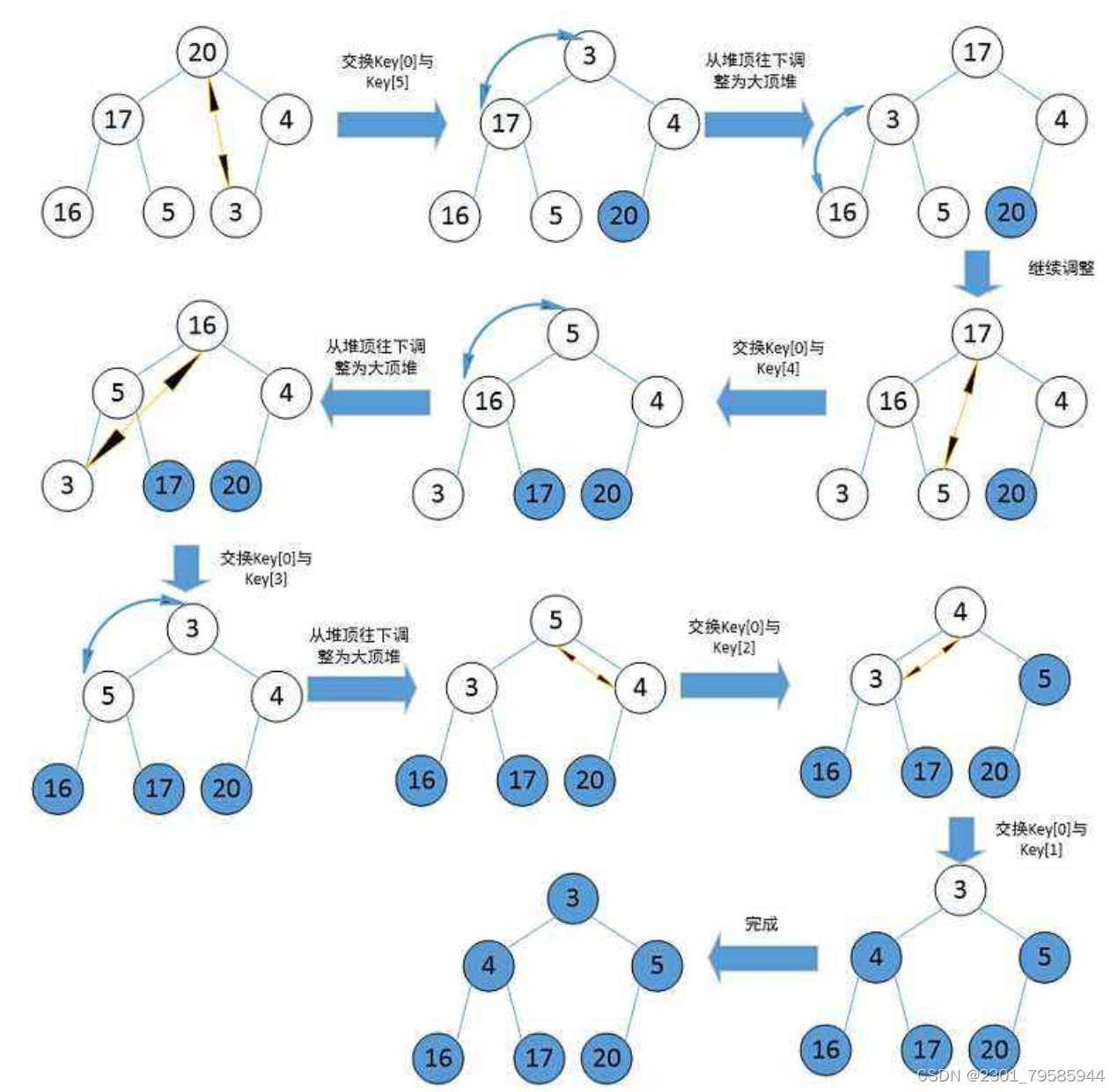
直接选择排序的特性总结:
1. 堆排序使用堆来选数,效率就高了很多。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
2.2堆排序的代码实现
堆排序的代码实现,请点击这里!
总结
好了,本篇博客到这里就结束了,如果有更好的观点,请及时留言,我会认真观看并学习。
不积硅步,无以至千里;不积小流,无以成江海。