机器学习周报第27周

摘要

本周阅读了一篇混沌时间序列预测的论文，论文模型主要使用的是时间卷积网络（Temporal Convolutional Network，TCN）、LSTM以及GRU。在数据集方面除了使用现实的时间序列数据外，还通过若干混沌系统生成了一些混沌的时间序列数据，这些数据没有现实方面的意义，但可以用来证明论文模型的实用性。因为混沌时间序列在现实世界普遍存在，例如水质，股票，天气等，所以论文模型也有运用于水质预测的潜力。

Abstract

This week, We read a paper on chaotic time series prediction. The paper primarily utilized models such as Temporal Convolutional Network (TCN), Long Short-Term Memory (LSTM), and Gated Recurrent Unit (GRU). In terms of the dataset, in addition to using real-world time series data, the paper also generated chaotic time series data through several chaotic systems. Although these chaotic data lack real-world significance, they serve to demonstrate the practicality of the proposed models. Given the prevalence of chaotic time series in the real world, such as in water quality, stock markets, and weather patterns, the models presented in the paper hold potential for applications in water quality prediction.

一、文献阅读

论文标题：Temporal Convolutional Networks with RNN approach for chaotic time series prediction

论文摘要
混沌时间序列（Chaotic Time Series）的预测构成了科学与工程领域的许多系统，近年来成为研究者关注的焦点。混沌时间序列预测是使用先前观测到的数据对具有已知初始条件的非线性混沌系统进行未来预测。混沌时间序列预测可以应用于天气预报、金融和股票市场等许多领域。许多学科致力于解决时间序列预测问题，从提前几天预测天气事件到交易者预测股票的未来。在最近的研究中，已经知道到混合深度神经网络方法在解决时间序列预测问题方面具有更好的性能，并且因为从解决此类问题的多种方法的优势中受益而使得其越来越受欢迎。本文提出了一种用于混沌时间序列预测的混合深度神经网络架构。所使用的混合方法包括时间卷积网络，用于从输入和递归神经网络层中提取低级特征，例如长短期记忆和门控递归单元，以捕获时间信息。

问题描述
自然界中许多随时间变化的系统的数学模型具有动态系统属性，这些系统会产生混沌数据并对其进行操作。虽然混沌还没有一个普遍接受的定义，但它是以非线性系统的形式出现的，产生对初始条件敏感的非周期性输出。混沌信号是具有连续功率谱的类噪声信号。这些信号可以在自然界中找到，例如流体流动、心跳不规则、天气和气候数据，以及许多具有现实生活模式的系统，例如股票市场和道路交通。随着混沌时间序列预测研究的成功率的提高，对于这些难以预测的过程的未来情况，将有可能进行预防和准备。目前，研究人员对混沌脑电图(EEG)、载波振动、臭氧浓度、太阳活动、风速等包含混沌时间序列的系统进行未来预测，并根据这些预测提供必要的系统控制。混沌时间序列预测已成为最近研究人员最感兴趣的时间序列问题之一。其原因是自然界中的许多系统都表现出动态行为，并且随着混沌时间序列的预测成为可能，自然界中的许多现象将变得可预测。

过去方案
早期的预测研究中使用的传统自回归和移动平均预测方法也被用于时间序列，但由于其线性性质，它们的预测性能较低。因此，人工神经网络（ANN）和机器学习（ML）算法在2000年已经取代了时间序列预测问题的统计方法，因为它们在处理非线性方面取得了很高的成功。通过将ANN、ML与统计方法相结合，相比较单个预测算法往往能得到更高的精度。自2010年以来，深度神经网络（DNN）的使用已开始在研究中广泛使用。DNN广泛用于时间序列预测问题，可分为四种主要网络架构：Elman循环神经网络（ERNN）、卷积神经网络（CNN）和时间卷积网络（TCN）。通过对真实世界工程测试用例的实验研究，观察到与19种不同的方法相比，ERNN架构给出了更准确的预测。除了在时间序列预测问题中使用 ERNN之外，LSTM是另一种递归神经网络架构，包含可以存储过去输入信息的门，近年来也在该领域得到了广泛的应用。CNN结构通常用于二维数据处理，在解决分类问题中占有重要地位，近年来也被用于时间序列数据的预测，并且已经观察到CNN结构在时间序列预测问题中取得了高性能的结果。

论文方案
该文提出了一种由不同神经网络层组合而成的混合模型，即时间卷积神经网络（TCN）和循环神经网络（RNN）。主要由TCN 、LSTM和GRU层组成的RNN架构的TCN来解决混沌时间序列预测问题。TCN有助于提取时间序列中短时间内发生的变化特征，而LSTM揭示了长时间内发生的变化特征，GRU具有有效的非线性拟合能力。通过这种方式，可以对分布在宽频谱上的所有特征进行建模。在所使用的模型中，TCN提取时间序列的一维空间特征，并将这些特征向量提供给RNN。将两个网络一起训练，从而获得两轮特征提取和两轮数据杂质过滤。由于TCN已经大大减少了数据杂质，因此随后的RNN阶段可以更有效地工作并更好地提取序列特征。

时间卷积神经网络（TCN）
通常认为，卷积神经网络非常适合用于图像处理任务，但实际上它也适用于时间序列预测任务。卷积操作有一维卷积和二维卷积两种方式，当卷积神经网络用于处理时间序列时，通常是对时间序列进行一维卷积。所谓的一维卷积就是从上至下、依据样本的顺序对矩阵进行扫描点积并生成一个新序列的计算方式。与图像处理的二维卷积一样，可以创建多个卷积核对同一组数据进行多次扫描，使得算法以不同的角度来解读同样的数据。
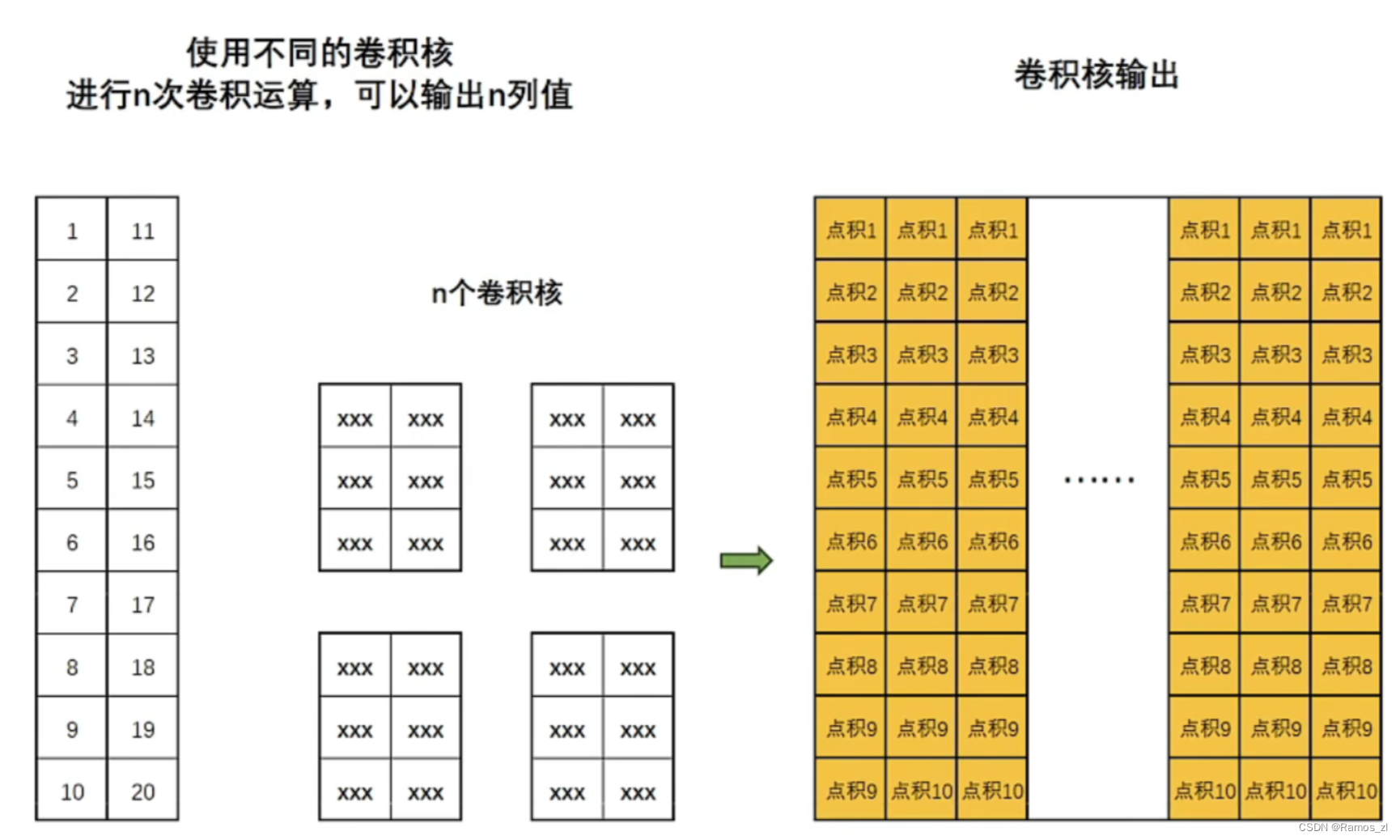
在这里插入图片描述
而且还可以在卷积的基础上再做卷积，通过多层卷积来放大感受野，使得最深层次的输出结果能考虑到更大范围的时间序列数据。例如下图中，第一层卷积的一次点积只考虑了原始时间序列的三行数据，而第二层卷积的一次点积则可以考虑原始时间序列的五行数据，更多层卷积下去考虑的也更多。
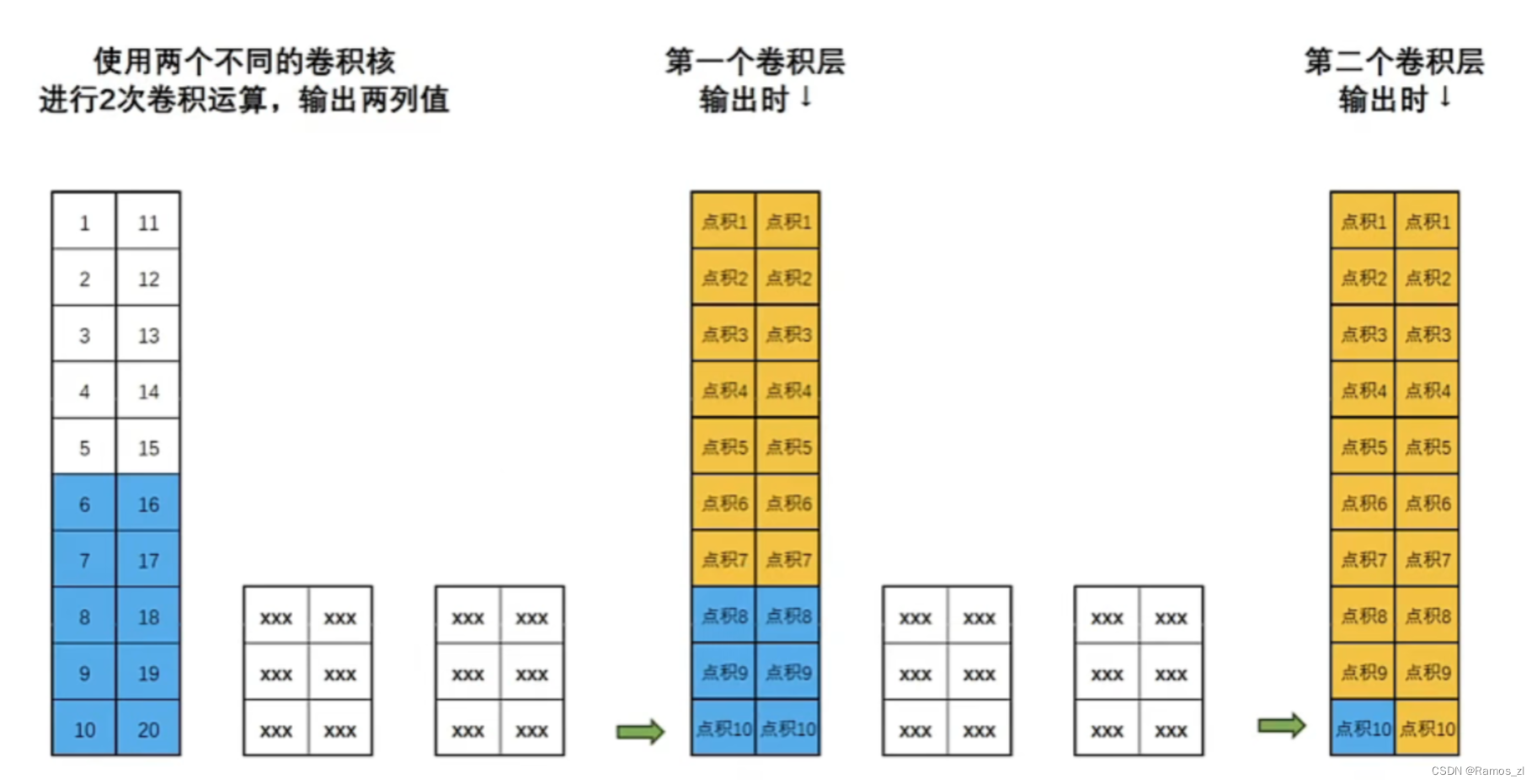
在这里插入图片描述
因果卷积（Causal Convolutions）
在处理时间序列数据时，特别是在预测未来的时刻，我们不希望未来的信息在当前时刻被考虑。比如说在下图t=1时刻进行的卷积实际上是参考了未来t=2和t=3时刻的数据，也就是说我们在用未来的数据在进行当前时刻的预测，这显然和我们期望的不一样。
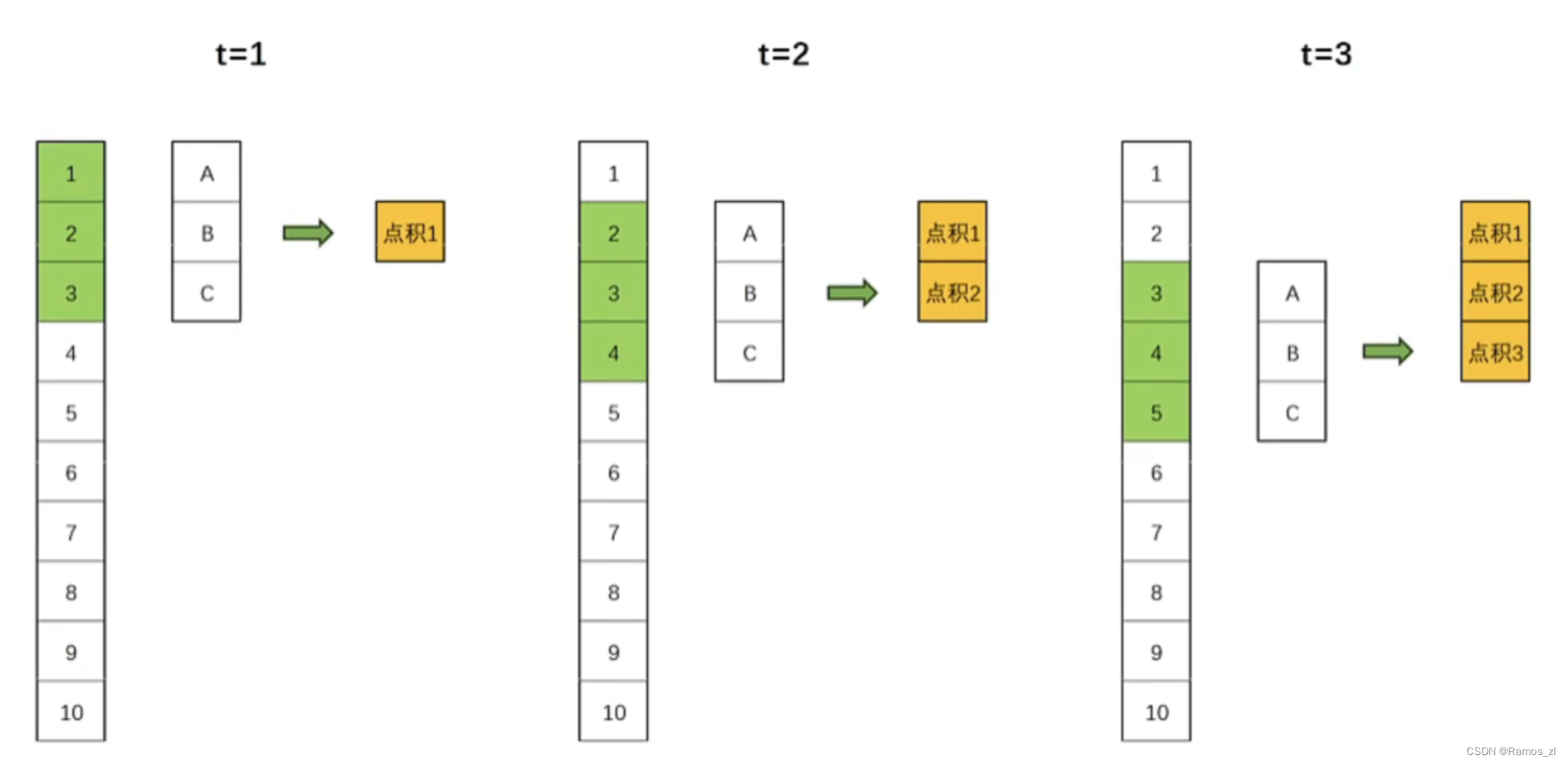
在这里插入图片描述
因此就引入了因果卷积的概念。因果卷积保证了在任何时间点t，输出只依赖于时间点t及其之前的输入，而不依赖t之后的输入。因果卷积可以通过对输入数据进行适当的“填充"来实现。具体地说，假设我们有一个一维的输入序列和一个大小为k的卷积核，为了实现因果卷积，我们可以在序列的开始处填充k-1个零，然后进行标准的卷积操作。这样，卷积的输出在任何时间点t都只会依赖于时间点t及其之前的输入，如下图所示：
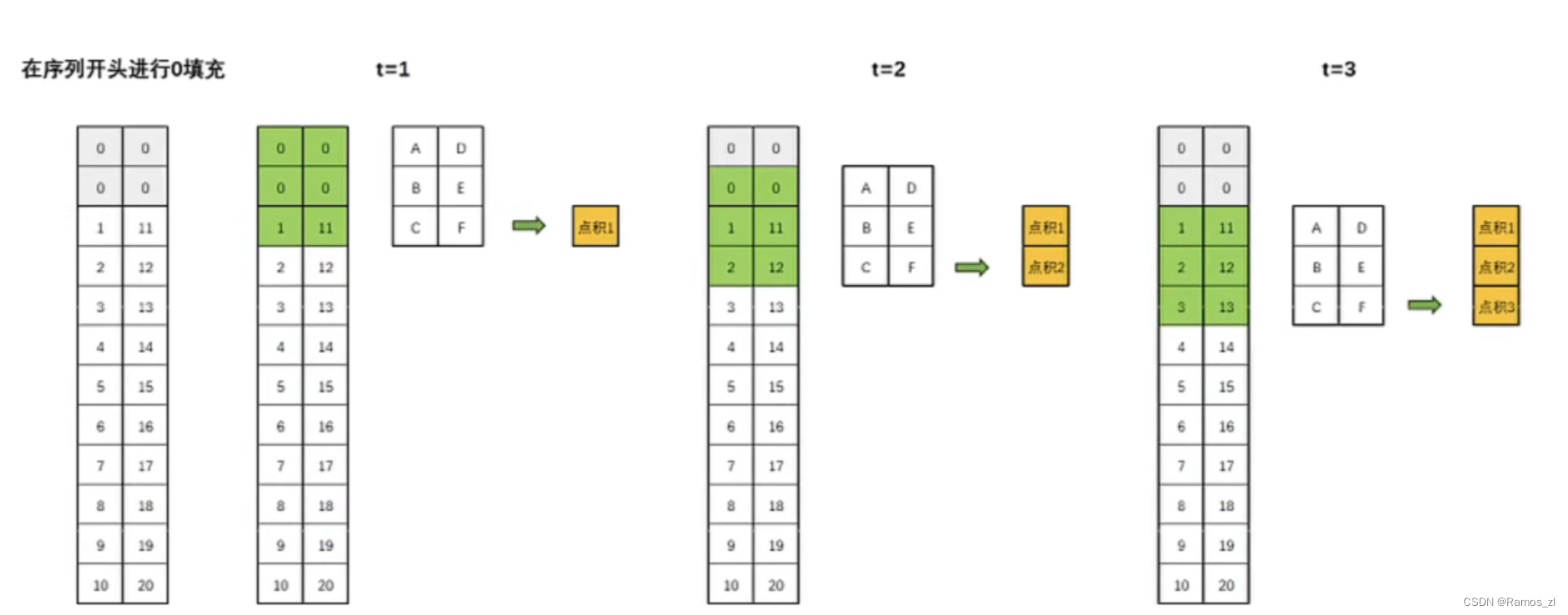
在这里插入图片描述
膨胀卷积（Dilated Convolutions）
膨胀卷积是TCN中的关键组件，它可以通过对卷积核填上“空洞"的方式来放大卷积层的感受野。填补空洞的方式是卷及操作中常见的方式，这种方式无需增加模型参数或计算成本，就可以轻松放大感受野。在标准的卷积中，卷积核的元素是连续的，一次覆盖输入数据的连续部分。而在膨胀卷积中，卷积核的元素之间存在间隔，这些间隔使得卷积核可以覆盖更广的范围。如下图所示，当我们使用膨胀指数为1时，就是在原始卷积核的每行中填补一行0。
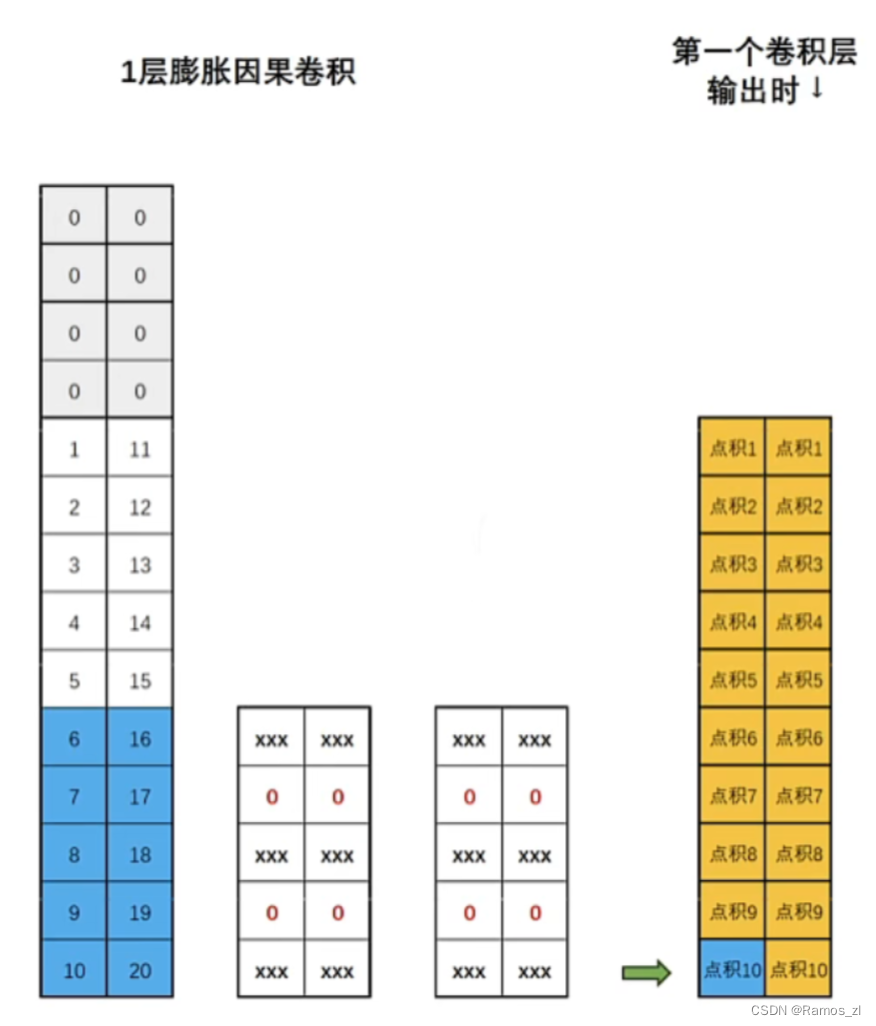
在这里插入图片描述
虽然添0会让卷积核在一次点积运算中损失一部分时间序列的信息，但是也让卷积核看到了“更远的过去”，在很大程度上放大了感受野的范围，而且这种放大不会增加额外的训练参数。值得注意的是，就算某些数据在这一次的卷积中未被捕获，在上一次或者下一次的卷积中还是会被考虑到的，所有这种损失是可以接受的。
在这里插入图片描述
很显然，如果我们使用更大的膨胀指数，那感受野就可以被放得更大。在TCN当中，原作者建议的膨胀指数是第一个卷积层使用1，第二个卷积层使用2，第三个卷积层使用4，这种结构可以使网络的顶层捕捉到非常长的时间依赖关系，而底层则可以捕捉到更短的依赖关系。本篇论文也是使用的这样的卷积指数。
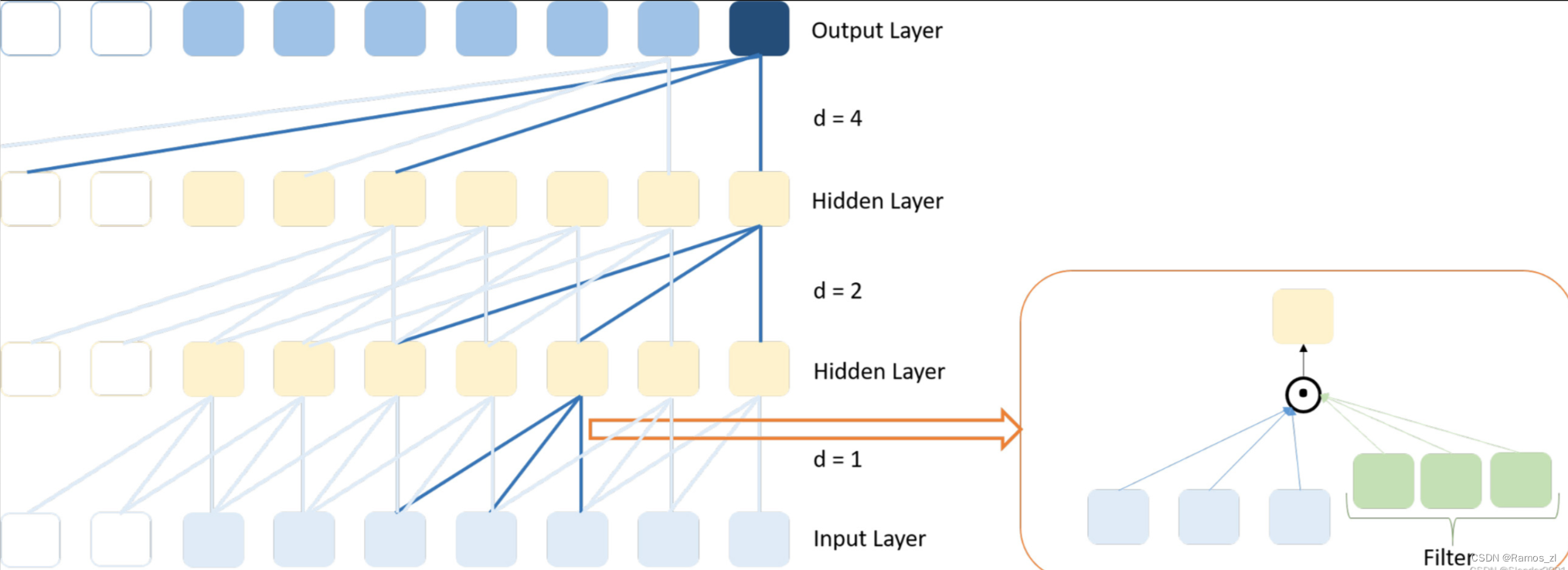
在这里插入图片描述
残差块（Residual Block）
残差块（或残差链接）是深度学习中一种增强网络训练稳定性的技术。它首次由He等人在2015年的文章中提出，用于解决深层网络中的梯度消失和梯度爆炸问题。这种设计后来在多种网络架构中被广泛采用，包括TCN。在TCN中，残差块的主要目的是帮助模型学习不同时间尺度上的依赖关系，并确保深度增加时的训练稳定性。在残差连接的设计中，当前层的输出不仅传递给下一层，而且与输入直接相加，从而形成一个"短路"连接。这种设计允许信息直接流过多个层，提供了一种更直接的路径更新梯度。一个残差块本质上是由膨胀因果卷积和1x1卷积组成的，多个残差块串联堆叠就成了一个TCN。
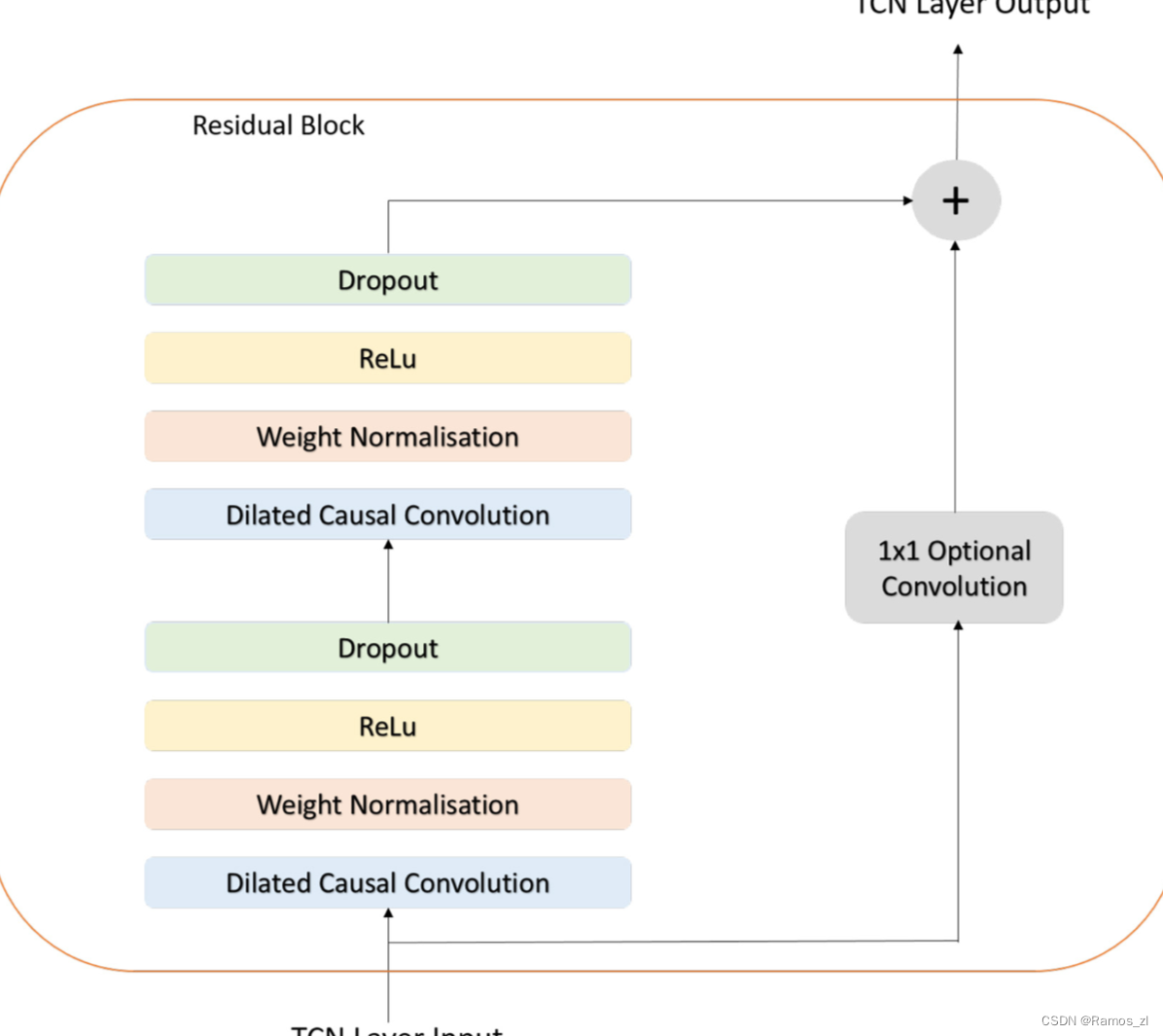
在这里插入图片描述
论文模型
本文提出了一种将时间卷积神经网络与递归神经网络相结合的时间序列预测方法。当研究时间序列预测文献时，值得注意的是，TCN架构在解决大多数预测问题时比LSTM和GRU表现更好，并且大多数研究都研究了多少层堆叠的TCN层能给出最好的结果。由于TCN本身的结构，随着层数的增加，卷积层的计算负荷增加，模型并不总是给出更成功的结果。在本研究提出的混合结构中，TCN被用作第一个DNN层，在广泛的感受野中提取低级特征。特征的时间信息，即TCN层的输出，在下一步与RNN层一起处理，以充分利用混沌时间序列。本文提出了两种不同的混合方法。如下图所示，第一种方法是在TCN层输出后使用LSTM和Dense Layer进行预测，第二种方法是在TCN层输出后使用GRU和Dense Layer进行预测。在本研究范围内，使用TCN层将数据转换为模式，然后使用RNN层将模式传输到具有记忆门的未来时间，从而提高了时间序列的预测性能。
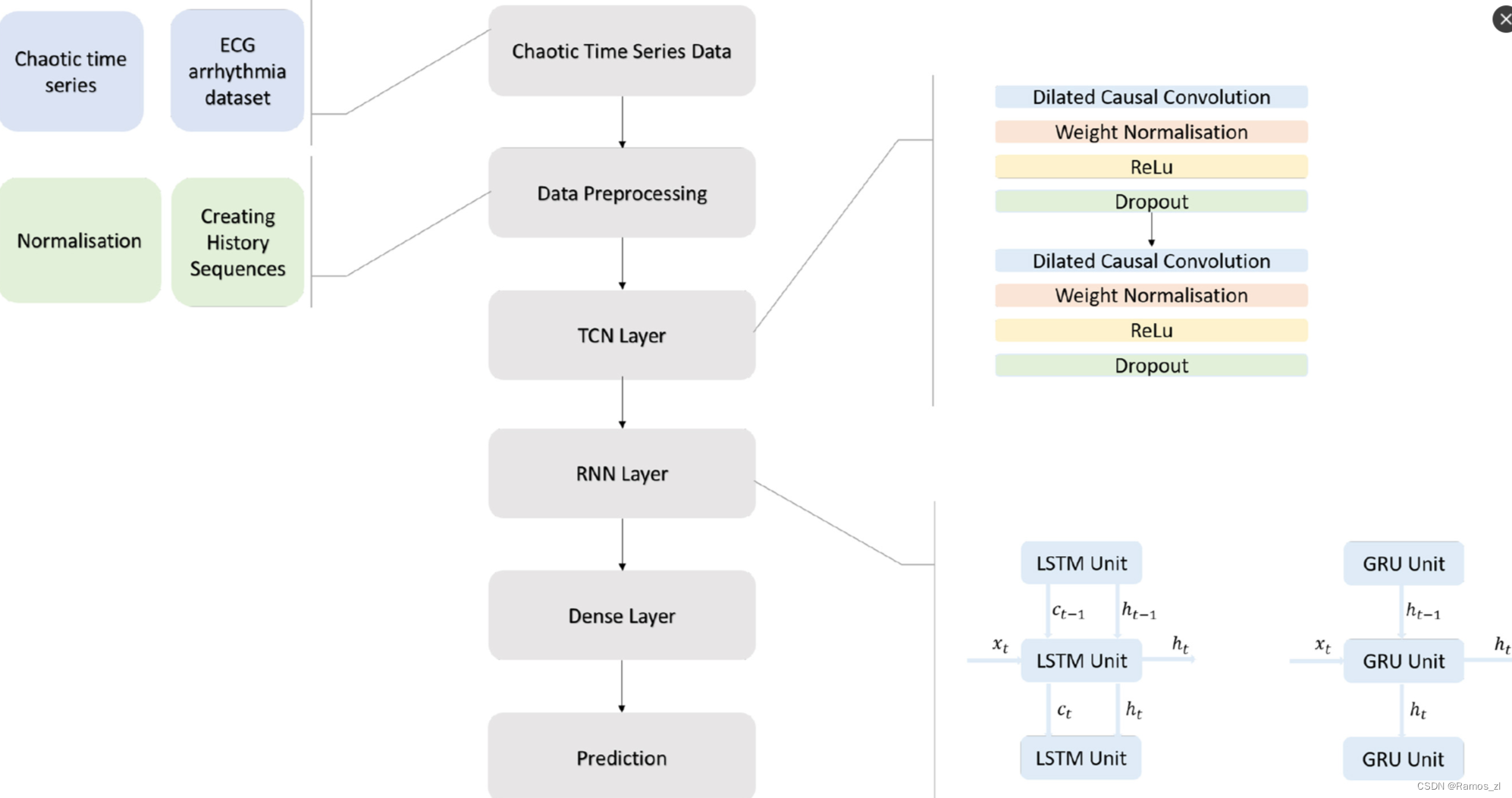
在这里插入图片描述
数据集
该文采用两种不同的混沌时间序列数据集对混沌时间序列进行预测的基准研究。首先，利用常用的经典动力系统：Lorenz、Rössler和类Lorenz混沌系统方程组得到混沌时间序列数据。此外，作为一个现实生活中的例子，对于MIT-BIH心律失常数据库中的21名患者，每个患者将100,000个时间步长ECG（心电图）数据分为训练，验证和测试三个部分。对于这两个数据集，训练数据分离了40,000个时间步，验证数据分离了10,000个时间步，测试数据分离了50,000个时间步。

相关代码
TCN模型定义

import torch
import torch.nn as nn
from torch.nn.utils import weight_norm
 
 
class Chomp1d(nn.Module):
    def __init__(self, chomp_size):
        super(Chomp1d, self).__init__()
        self.chomp_size = chomp_size
 
    def forward(self, x):
        """
        裁剪模块，裁剪多出来的padding
        """
        return x[:, :, :-self.chomp_size].contiguous()
 
 
class TemporalBlock(nn.Module):
    def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
        """
        相当于一个Residual block
        :param n_inputs: int, 输入通道数
        :param n_outputs: int, 输出通道数
        :param kernel_size: int, 卷积核尺寸
        :param stride: int, 步长，一般为1
        :param dilation: int, 膨胀系数
        :param padding: int, 填充系数
        :param dropout: float, dropout比率
        """
        super(TemporalBlock, self).__init__()
        self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        # 经过conv1，输出的size其实是(Batch, input_channel, seq_len + padding)
        self.chomp1 = Chomp1d(padding)  # 裁剪掉多出来的padding部分，维持输出时间步为seq_len
        self.relu1 = nn.ReLU()
        self.dropout1 = nn.Dropout(dropout)
 
        self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        self.chomp2 = Chomp1d(padding)  #  裁剪掉多出来的padding部分，维持输出时间步为seq_len
        self.relu2 = nn.ReLU()
        self.dropout2 = nn.Dropout(dropout)
 
        self.net = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
                                 self.conv2, self.chomp2, self.relu2, self.dropout2)
        self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
        self.relu = nn.ReLU()
        self.init_weights()
 
    def init_weights(self):
        """
        参数初始化
        :return:
        """
        self.conv1.weight.data.normal_(0, 0.01)
        self.conv2.weight.data.normal_(0, 0.01)
        if self.downsample is not None:
            self.downsample.weight.data.normal_(0, 0.01)
 
    def forward(self, x):
        """
        :param x: size of (Batch, input_channel, seq_len)
        :return:
        """
        out = self.net(x)
        res = x if self.downsample is None else self.downsample(x)
        return self.relu(out + res)
 
 
class TemporalConvNet(nn.Module):
    def __init__(self, num_inputs, num_channels, kernel_size=2, dropout=0.2):
        """
        TCN，目前paper给出的TCN结构很好的支持每个时刻为一个数的情况，即sequence结构，
        对于每个时刻为一个向量这种一维结构，勉强可以把向量拆成若干该时刻的输入通道，
        对于每个时刻为一个矩阵或更高维图像的情况，就不太好办。
        :param num_inputs: int， 输入通道数
        :param num_channels: list，每层的hidden_channel数，例如[25,25,25,25]表示有4个隐层，每层hidden_channel数为25
        :param kernel_size: int, 卷积核尺寸
        :param dropout: float, drop_out比率
        """
        super(TemporalConvNet, self).__init__()
        layers = []
        num_levels = len(num_channels)
        for i in range(num_levels):
            dilation_size = 2 ** i   # 膨胀系数：1，2，4，8……
            in_channels = num_inputs if i == 0 else num_channels[i-1]  # 确定每一层的输入通道数
            out_channels = num_channels[i]  # 确定每一层的输出通道数
            layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1, dilation=dilation_size,
                                     padding=(kernel_size-1) * dilation_size, dropout=dropout)]
 
        self.network = nn.Sequential(*layers)
 
    def forward(self, x):
        """
        输入x的结构不同于RNN，一般RNN的size为(Batch, seq_len, channels)或者(seq_len, Batch, channels)，
        这里把seq_len放在channels后面，把所有时间步的数据拼起来，当做Conv1d的输入尺寸，实现卷积跨时间步的操作，
        很巧妙的设计。
        
        :param x: size of (Batch, input_channel, seq_len)
        :return: size of (Batch, output_channel, seq_len)
        """
        return self.network(x)

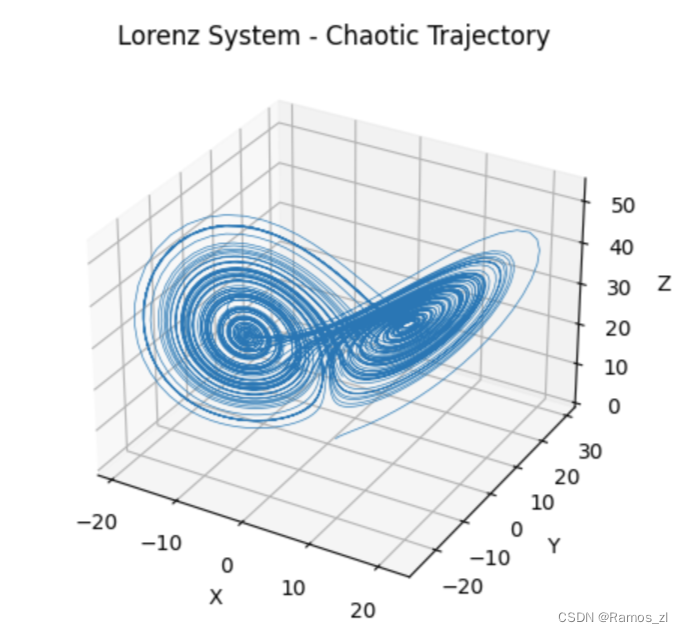
论文参数下的Lorenz系统

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
 
def lorenz_system(num_steps, sigma=10, rho=28, beta=8/3, initial_state=None):
    dt = 0.01
    if initial_state is None:
        state = np.array([0.1, 0.0, 0.0])
    else:
        state = np.array(initial_state)
    trajectory = [state]
 
    for _ in range(num_steps):
        dx = sigma * (state[1] - state[0])
        dy = state[0] * (rho - state[2]) - state[1]
        dz = state[0] * state[1] - beta * state[2]
 
        state = state + np.array([dx, dy, dz]) * dt
        trajectory.append(state.copy())
 
    return np.array(trajectory)
 
# 生成 Lorenz 系统轨迹
num_steps = 10000
initial_state = [0.9, 0.9, 0]
trajectory = lorenz_system(num_steps=num_steps, initial_state=initial_state)
 
# 绘制 Lorenz 系统轨迹
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(trajectory[:, 0], trajectory[:, 1], trajectory[:, 2], lw=0.5)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Lorenz System - Chaotic Trajectory')
plt.show()