算法第十三天-组合总和Ⅱ

news2024/9/25 1:17:54

组合总和Ⅱ

题目要求

解题思路

按顺序搜索，设置合理的变量，在搜索的过程中判断是否会出现重复集结果。重点理解对输入数组排序的作用和参考代码中大剪枝和小剪枝的意思

这道题域上一问的区别在于：

第39题：candidates中的数字可以无限制重复被选取；
第40题：candidates中的每个数字在每个组合中只能使用一次；

相同点在于：相同数字列表的不同排列被视为一个结果。

如何去掉重复的集合（重点）
为了使得解集不包含重复的组合。可以从以下两种方案思考：

使用 hash 天然去重功能，但是编码相对复杂；
使用和第39题和第15题相似的思路：不重复就不需要按顺序搜索，**在搜索过程中检测分支是否会出现重复结果。**注意：在这里的顺序不仅仅指数组candidates有序，还指按照一定顺序搜索结果。

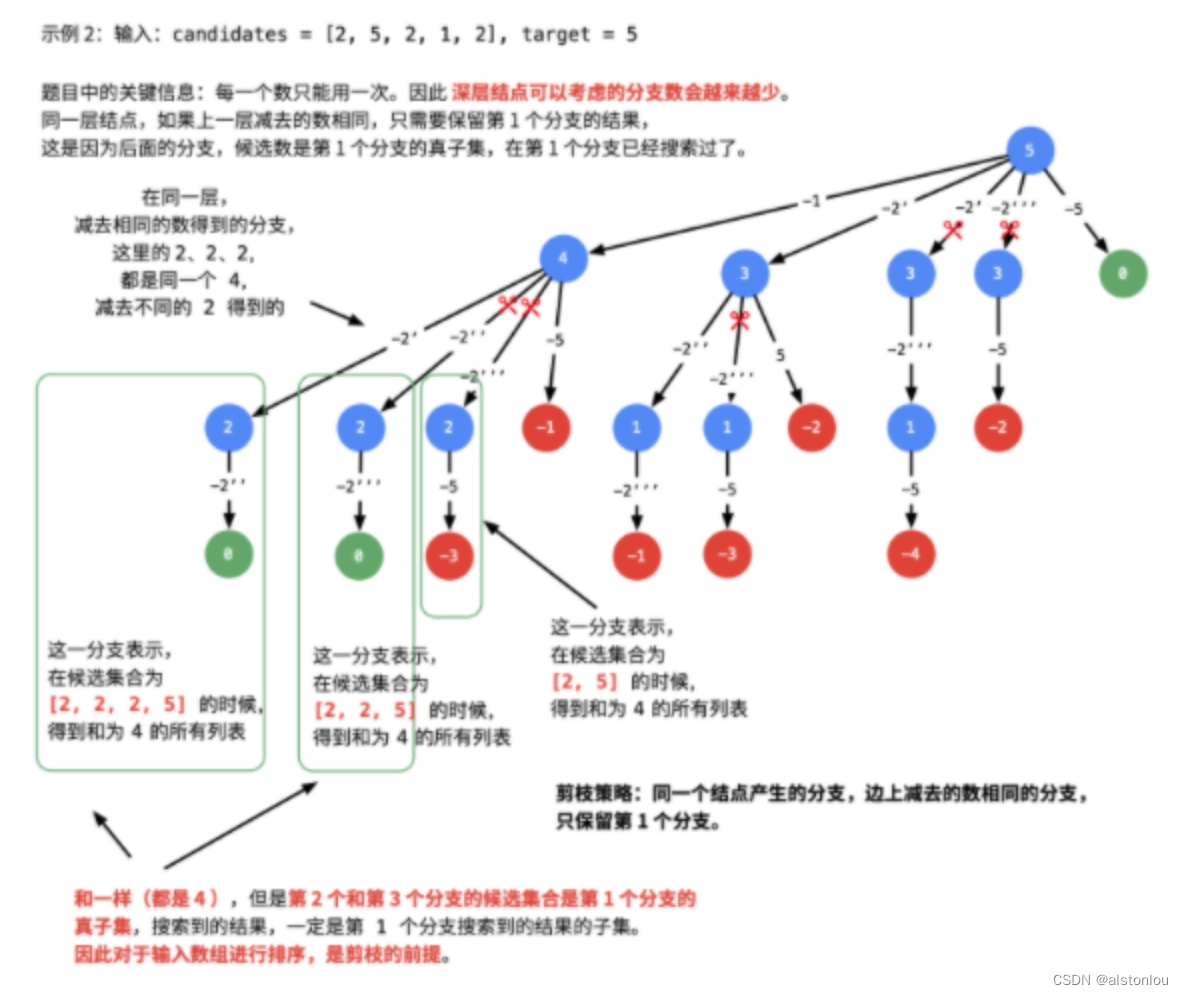
由39题我们知道，数组candidates有序，也是DFS 过程中实现[剪枝]的前提。
将数组先排序的思路来自于这个问题：去掉一个数组中重复的元素。很容易想到的方案是：先对数组升序排列，重复的元素一定不是排好序以后相同的连续数组区域的第1个元素。也就是说，剪枝发生在：**同一层数值相同的节点第2，3，…个节点，因为数值相同的第1个节点已经搜索出了包含了这个数值的全部结果，**同一层的其他节点，候选数的个数更少，搜索出的结果一定不会比第1个节点更多，并且是第一个节点的子集。

代码

from typing import List
class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        def dfs(begin, path, residue):
            if residue == 0:
                res.append(path[:])
                return
            for index in range(begin, size):
                if candidates[index] > residue:
                    break
                if index > begin and candidates[index - 1] == candidates[index]:
                    continue
                path.append(candidates[index])
                dfs(index + 1, path, residue - candidates[index])
                path.pop()
        size = len(candidates)
        if size == 0:
            return []
        candidates.sort()
        res = []
        dfs(0, [], target)
        return res