【题目来源】
http://acm.hdu.edu.cn/showproblem.php?pid=1205

【题目描述】
HOHO，终于从Speakless手上赢走了所有的糖果，是Gardon吃糖果时有个特殊的癖好，就是不喜欢将一样的糖果放在一起吃，喜欢先吃一种，下一次吃另一种，这样；可是Gardon不知道是否存在一种吃糖果的顺序使得他能把所有糖果都吃完？请你写个程序帮忙计算一下。

【输入格式】
第一行有一个整数T，接下来T组数据，每组数据占2行，第一行是一个整数N（0<N<=1000000)，第二行是N个数，表示N种糖果的数目Mi(0<Mi<=1000000)。

【输出格式】
对于每组数据，输出一行，包含一个"Yes"或者"No"。

【输入样例】
2
3
4 1 1
5
5 4 3 2 1

【输出样例】
No
Yes

【算法分析】
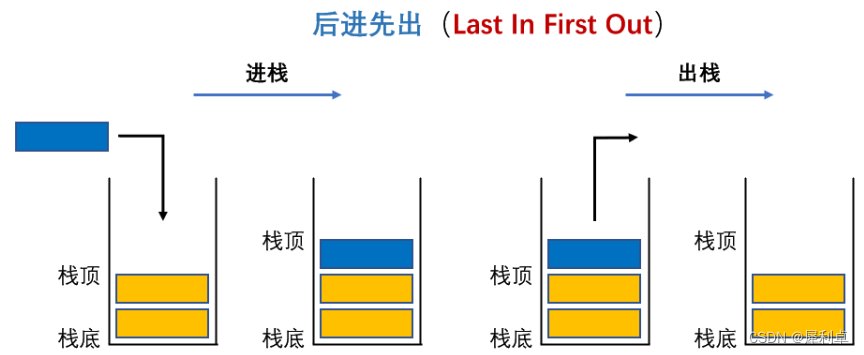
鸽巢原理（Pigeonhole Principle），或称抽屉原理（Drawer Principle）。
鸽巢原理常见的两种表述如下所述：
● 将 个物体，划分为  组，那么有至少一组有两个（或以上）的物体。
● 将 个物体，划分为  组，那么至少存在一个分组，含有大于或等于  个物品。

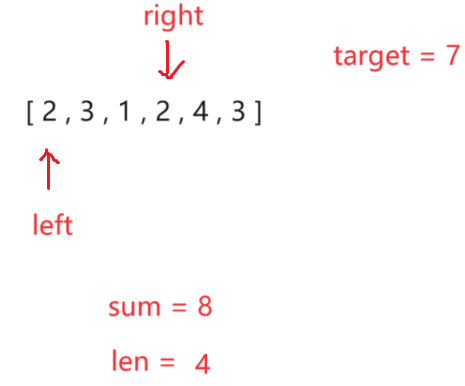
本题是鸽巢原理的典型应用：若设数量最多的某种糖果数为 N，其他糖果总数为 S。若视 N 个糖果为 N 个隔板，并把每个隔板的右边看成一个空间，则可隔成 N 个空间。

若 S<N-1（也即，N>S+1），则至少有两个隔板之间没有糖果，而隔板代表同一种糖果，故无解。
若 S>=N-1（也即，N<=S+1），肯定有解。

依据一种取巧的方法，“若整数位数超过10位，就选择用 long long 型”。故本题中的若干变量不定义为 int 型，而定义为 long long 型，因为计算过程中，极大可能会超过 10 位数。

【算法代码】

#include <iostream>
using namespace std;

typedef long long LL;
LL imax,sum;
LL n,x;

int main() {
    LL T;
    scanf("%lld",&T);
    while(T--) {
        imax=0;
        sum=0;
        scanf("%lld",&n);
        while(n--) {
            scanf("%lld",&x);
            if(imax<x) imax=x;
            sum+=x;
        }
        sum-=imax;
        if(imax<=sum+1) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}


/*
in:
2
3
4 1 1
5
5 4 3 2 1

out:
No
Yes
*/

【参考文献】
https://blog.csdn.net/blue_skyrim/article/details/46126049
https://blog.csdn.net/weixin_45696704/article/details/114483453
https://zhuanlan.zhihu.com/p/661206530