之前一直以为二分查找有什么难的,不就是确定左右边界,然后while循环求mid,大于mid的找右半边,小于mid的找左半边。直到最后相同了就是最后查找的结果了.
后来等真正用到二分查找算法的时候,发现问题远没有这么简单,上述的查找确实可以查找一个指定值x,但是x的具体位置,我们并不清楚.所以有一道题,就是给定一个数组,求出指定值x的左右边界,若没有返回-1,例如数组:
1 2 2 3 3 4然后分别查询3,4,5.
预期结果应为
3 4
5 5
-1 -1利用我们课堂上所讲的二分查找,根本无法解决这类问题,所以这里介绍一下二分算法的真正写法以及应用场景.(注:根据y总的方法所总结).
这里先放一个原题链接:
数的范围
这里直接给出二分查找的步骤,后面我会逐一讲解:
- 找一个区间[L,R],使得答案一定在该区间中
- 找一个判断条件,使得该判断条件具有二段性,并且答案(要查找的值)一定是该二段性的分界点
- 分析终点mid在该判断条件下是否成立,如果成立,考虑答案在哪个区间;若不成立,考虑答案在哪个区间(即我们平常写二分时所用的if else语句)
- 如果更新方式是right = mid,则对mid不用做任何处理;如果更新方式是left = mid,则需要在计算mid是加上1.(这句话不懂没关系,记住就行,后面也会给出解释.)
第一点,一般都是L=0,R=n-1,这个很好确定.
看下第2点,我们提到了二段性,先来讲一下什么是二段性:
简单来说,二段性是指把数组分成两段,一段里面是满足条件的,而另一段是不满足的.
例如1,2,2,3,3,4,5,6.
假设我们要查找的数字是3,那么我们只能这两种情况分:
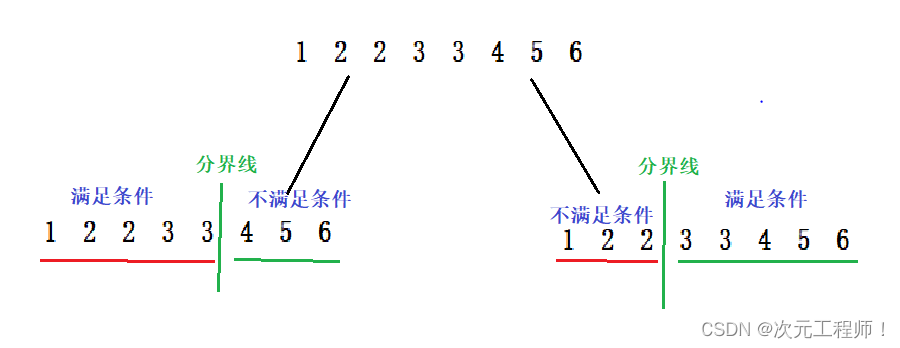
而不能是这样:

这样大家就能理解什么是二段性了.
接下来看第2点中的“答案(要查找的值)一定是该二段性的分界点”,什么意思呢?
我们假设此时要 求3的左边界,此时按照二段性,我们应该划分为上图的第二种情况,因为我们要找的答案一定是二段性中右侧的左端点,如下:
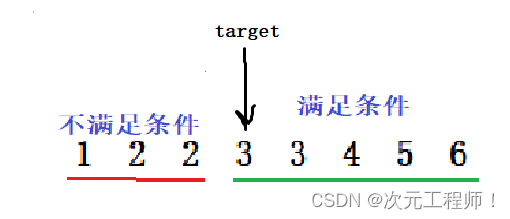
此时target的右侧一定是大于等于target的!
接下来看第三步,开始分析mid,更新边界.
假设mid在绿色部分(你不用结合数字分析,就理解为一种抽象的逻辑,mid是随便画的位置),如下:
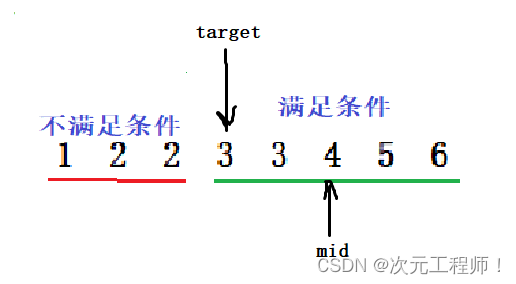
此时若arr[mid] >= target,说明需要将right = mid(注意这一步,下面第四步要说),注意不能是mid-1,因为当前这个mid值可能就是结果,毕竟mid在target的右侧或者正好就是它自己.
假设mid在红色部分,如下:
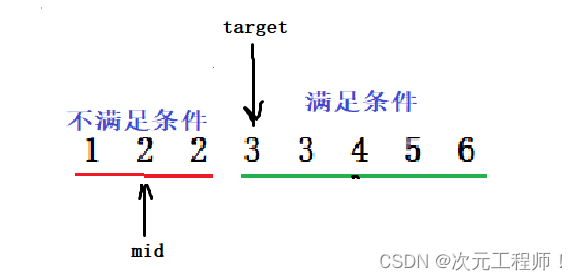
相应的,此时arr[mid]一定是小于target的由于二段性,即arr[mid] < target. 所以此时target在右半部分,更新left = mid+1。这个时候为什么又要+1呢,这是由于mid最大才只可能在红色部分的最后一个,而由于二段性,mid一定不会是答案,所以left = mid+1.
这样第三步就完成了,紧接着看第四步:“如果更新方式是right = mid,则对mid不用做任何处理;如果更新方式是left = mid,则需要在计算mid是加上1.”
就是看是left = mid 还是 right = mid,上面我们是在判断左边界时,是right = mid,所以我们在计算mid时,不需要对mid做任何处理,只需要正常操作即可,“mid = left + right >> 1”.
代码如下:
int left = 0;
int right = n-1;
while(left < right)
{
int mid = left + right >> 1;
if(nums[mid] >= k) right = mid;
else left = mid+1;
}左边界求完了,接下来是求 右边界,按照步骤走:
第二步:找一个判断条件,使得该判断条件具有二段性,并且答案(要查找的值)一定是该二段性的分界点
上面说过了,这里也不再细说,这里一定是这种情况:
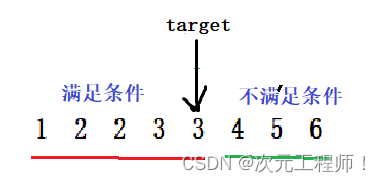
然后第三步,进行分析,然后更新边界.
此时target的左侧一定是小于等于target的!
当mid在红色区域时:
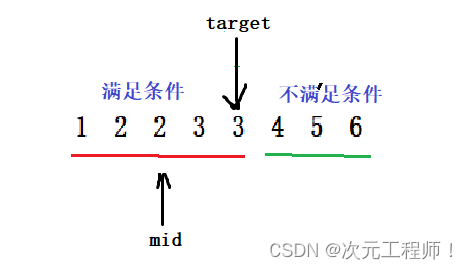
此时arr[mid] <= target,需要更新left = mid,注意不能是left = mid+1,还是和上面判断左边界一个道理,因为当前mid可能就是结果(因为在有结果的这一侧),加上会导致错误!
当mid在绿色区域时
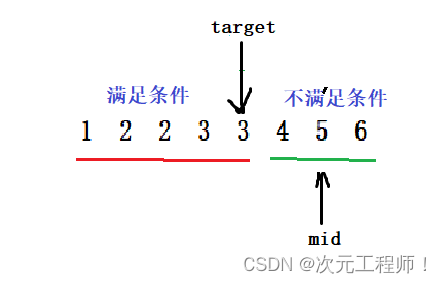
此时arr[mid]一定是大于target的,因为二段性,所以更新right = mid -1,这里-1 和上面所说的道理一模一样,mid最左只能在绿色的最左边,由于二段性,是不可能存在正确结果的,所以直接right=mid-1.
紧接着第四步,此时我们发现,判断右边界时,left=mid了,此时我们需要计算mid时处理一下,+1,即mid = left+right+1 >> 1.
代码如下:
int left = 0;
int right = n-1;
while(left < right)
{
int mid = left + right + 1>> 1;
if (nums[mid] <= k) left =mid;
else right = mid -1 ;
}所以,题的全部代码为:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n,q;
cin >> n >> q;
vector<int> nums(n+1);
for(int i = 0; i < n; i++)
{
cin >> nums[i];
}
while(q--)
{
int k = 0;
cin >> k;
int left = 0;
int right = n-1;
while(left < right)
{
int mid = left + right >> 1;
if(nums[mid] >= k) right = mid;
else left = mid+1;
}
if(nums[right] == k)
{
cout << right << " " ;
right = n-1;
while(left < right)
{
int mid = left + right + 1>> 1;
if (nums[mid] <= k) left =mid;
else right = mid -1 ;
}
cout << right << endl;
}
else
{
cout << -1 << " " << -1 << endl;
}
}
return 0;
}至此,二分查找的算法就讲解完毕了,现在是凌晨1点多,加之今天又复习了一天,写的可能有些省略了,如果你哪里不懂,欢迎评论区或者私信提问哦,最好是评论区,私信太多了,很大可能看不到,评论区一般都可以看到~