1、写作动机:
目前的从反馈中学习方法仅仅使用判断来促使LLMs产生更好的响应,然后将其作为新的示范用于监督训练。这种对判断的间接利用受到无法从错误中学习的限制,这是从反馈中学习的核心精神,并受到LLMs的改进能力的制约。
2、主要贡献:
• 首次系统地探讨了将LLMs与判断对齐的方法。
• 引入了一个新颖的框架CUT(对比不可能性学习),通过直接和明确地从判断中学习,促进了LLMs的对齐。值得注意的是,CUT允许基于判断进行细粒度的不当内容检测和校正。
3、背景知识-从反馈中学习:
从反馈中学习的现有方法可以分为两个不同的类别:提示和微调,它们通过LLMs的参数是否更新来区分。
提示: 提示不改变LLMs的参数。相反,它利用对先前响应的语言反馈,以促使生成更好的响应。
微调: 微调旨在直接训练一个更好的LLM。
4、将LLMs与判断对齐的预备知识:
假设有一组指令-响应-判断三元组(x,y,j),其中指令x = [x1,...,xM],响应y = [y1,...,yN],判断j = [j1,...,jQ]都是长度分别为M、N和Q的token序列。响应可能存在某些缺陷,或者被认为完全令人满意。判断提供了对响应的优点和缺点的分析。判断可以由人类标注员或AI评判模型起草。
将LLMs与判断对齐的目标是使LLM保留在优点中提到的适当行为,更重要的是解决弱点,以防止未来的错误行为。
一些先前的解决方案:
前向预测: 前向预测是指顺序预测响应及其判断的过程,具体来说,LLM在最大似然估计(MLE)目标下被训练,首先基于指令x生成响应y,然后基于组合序列[x,y]生成判断j。
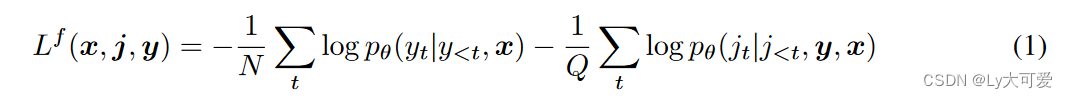
从语言反馈中的模仿学习: 从语言反馈中的模仿学习(ILF)要求LLM在给定反馈j的情况下改进初始响应y。改进后的响应yˆ,与初始指令x配对,用于在MLE目标下微调LLM。
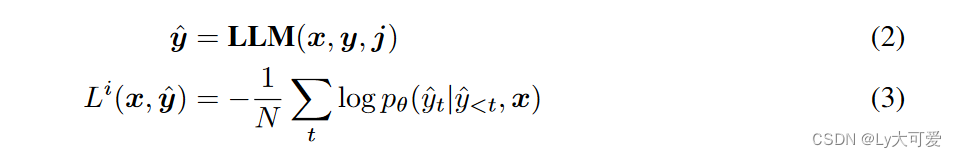
追溯法: 追溯法根据响应y收到的标量奖励重写指令x。例如,如果一个响应收到低于一定阈值的标量奖励,则在原始指令中添加短语“生成正确答案”;否则,添加“生成错误答案”。显然,这种方法可以自然地扩展到我们的问题设置中。具体来说,LLM被训练生成响应y,条件是序列[x,j]。

然而,在前向预测中,学习生成判断不一定会转化为增强的响应生成,因为响应生成先于判断生成。ILF只利用正面数据(即改进的响应),限制了模型识别和纠正在负面判断中强调的弱点或错误的能力。至于追溯法,使用不令人满意的响应作为MLE目标必然增加了生成不令人满意响应的风险。
5、CUT框架:
CUT的核心思想可以总结为从对比中学习。我们对不同条件下的响应生成进行对比,以阐明LLM应该保持的适当行为以及需要进行调整的具体内容。基于这些见解,对适当内容使用MLE训练,对不适当内容使用不可能性训练(UT)。
5.1将判断纳入对齐:
将指令-响应对称为“对齐”,如果响应忠实地遵循指令并满足人类期望 x −→ y。否则,判断描述了响应中存在的错误或缺陷。假设任务是生成一个有意满足判断的响应,可以推断出响应始终与组合输入 [x, j] −→ y 对齐。
Align-P:LLM对原始指令x生成满意的响应y。因此,授予积极的判断j以承认LLM的出色表现。很明显,响应y与指令x以及组合输入[x, j]都对齐。
Align-N:LLM在生成过程中出现了一些错误,导致响应y不满意。因此,负面判断j详细说明了相应的批评意见。对于Align-N,y在原始指令x方面不对齐。然而,考虑x和j作为整体,y确实与组合输入[x, j]对齐。
Misalign:在Align-N中的真实负面判断被替换为虚假的积极判断j。在这种情况下,响应y既不与原始指令x对齐,也不与组合指令和判断[x, j]对齐。
5.2 从对比中学习:
Align-N vs. Misalign:尽管Align-N和Misalign在x −→ y方面不对齐,但它们在任务[x, j] −→ y方面显示出相反的极性。由于LLMs具有强大的上下文学习能力,从Align-N到Misalign的对齐转换通常伴随着响应的生成概率下降,特别是对于与真实负面判断强相关的标记。
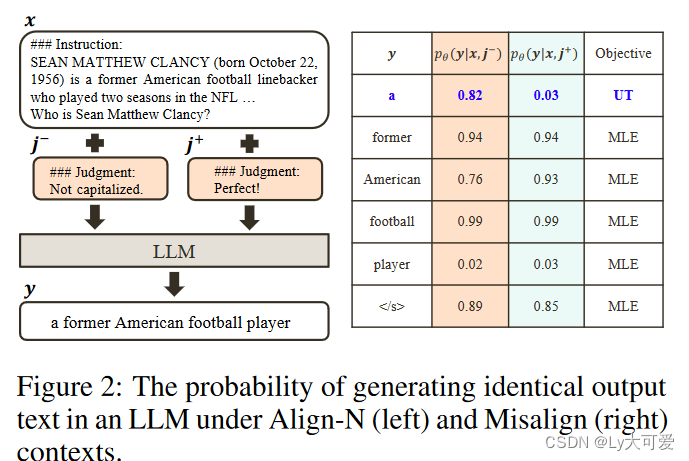
将Align-N和Misalign示例分别输入LLM以获取token生成概率pθ(yt|y<t, x, j −)和pθ(yt|y<t, x, j +)。将在条件为j −的情况下生成概率显著增加的与j +相比的token视为不适当的token(例如,图2中的“a”)。具体而言,采用以下标准:

其中λ≥1是一个超参数,用于权衡检测不适当token的精度和召回率。对识别的不适当token应用UT目标,以推动LLM探索替代生成。对于其他token,使用标准的MLE损失:

Align-P vs. Align-N:尽管Align-P和Align-N在[x, j] −→ y方面都对齐,但只有Align-P在仅考虑指令(x −→ y)时对齐。基本上,它表明LLM应根据是否引入负面判断来输出不同的响应。
具体而言,使用以下MLE目标训练这个比较:
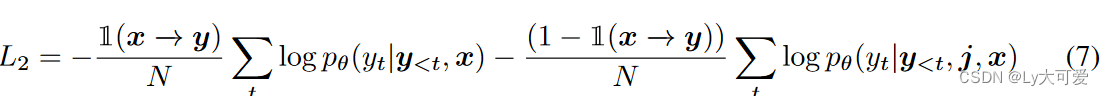
其中1(x −→ y)是一个指示函数,如果x和y对齐,则返回1,否则返回0。
最后,CUT的总体损失将这两个对比的损失函数结合在一起:LCUT=L1+L2。
6、实验:
在两种对齐设置中对CUT进行实验:(1)离线对齐,其中使用现成的与模型无关的指令-响应-判断三元组。 (2)在线对齐,其中判断是基于当前目标模型生成的响应进行的。这个在线设置可以进行迭代实现,允许持续的细化和适应。
使用LoRA进行模型训练,超参数λ的权衡选择自{1.1, 1.2, 1.5},不可能性权重α选择自{0.25, 0.5, 0.75, 1}。
6.1离线对齐:


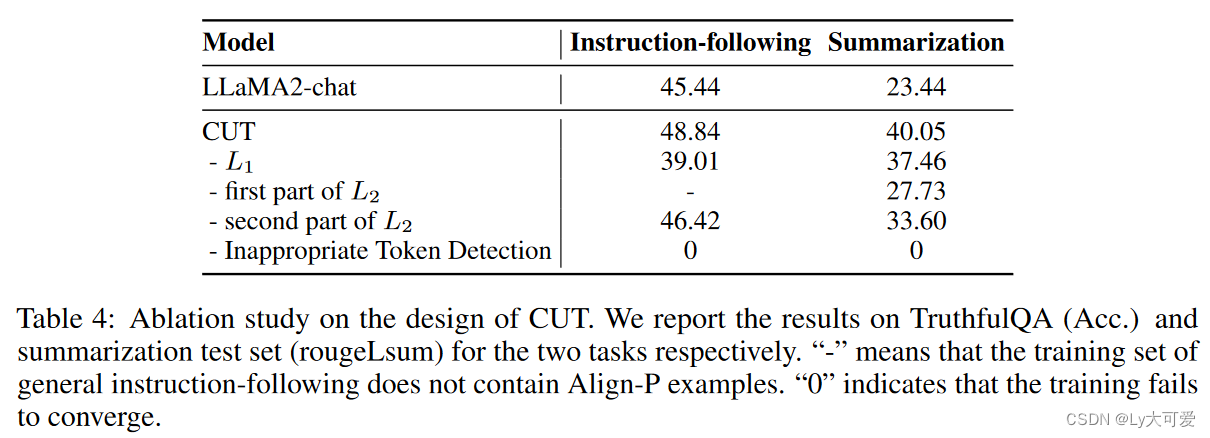
6.2在线对齐:
在线对齐过程可以迭代进行,类似于人类通过不断来自同行的反馈不断完善他们的行为。具体来说,我们重复应用以下三个步骤:
- 步骤1:收集指令x,并从目标模型获取响应y。
- 步骤2:为响应标注判断j。
- 步骤3:应用CUT通过{x, y, j}对目标模型进行微调。

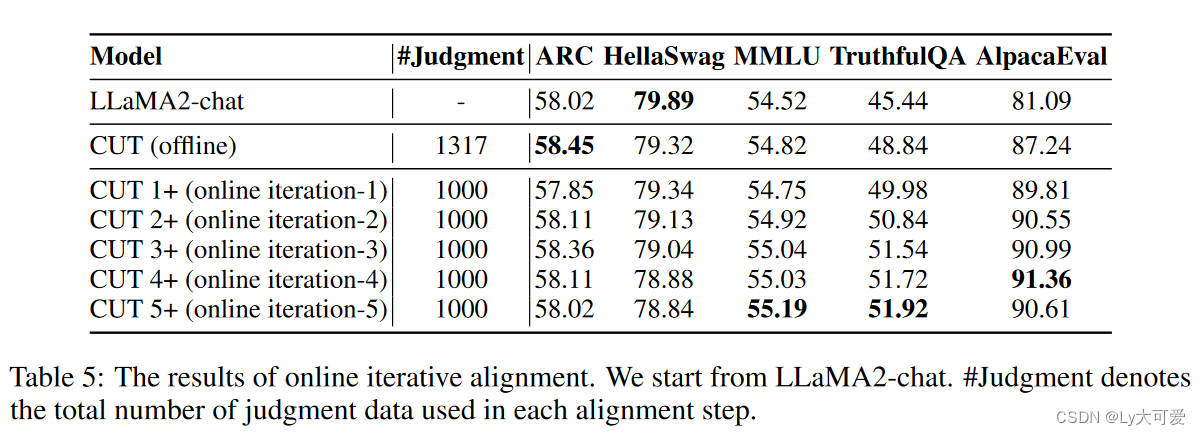
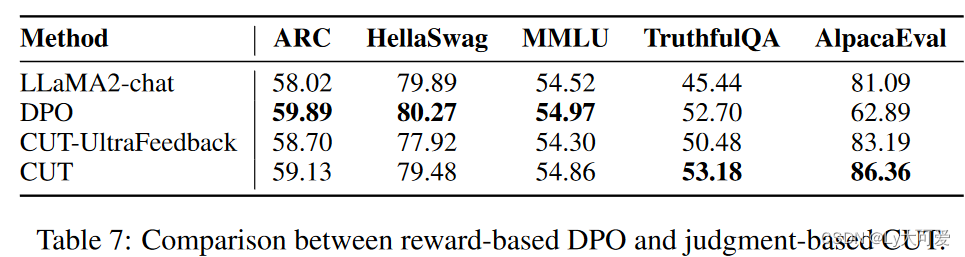
6.3判断vs奖励: