数据结构和算法-交换排序中的快速排序（演示过程 算法实现 算法效率 稳定性）

news2024/11/6 3:06:13

文章目录

  • 总览
  • 快速排序（超级重要）
  • 啥是快速排序
  • 演示过程
  • 算法实现
    • 第一次quicksort函数
    • 第一次partion函数
    • 到第一次quicksort的第一个quicksort
    • 到第二次quicksort的第一个quicksort
    • 到第二次quicksort的第二个quicksort
    • 到第一次quicksort的第二个quicksort
    • 到第一次quicksort的第二个quicksort的partition
    • 到第一次quicksort的第二个quicksort的第一个quicksort
    • 到第一次quicksort的第二个quicksort的第一个quicksort的partition函数
    • 到第一次quicksort的第二个quicksort的第一个quicksort的第一个quicksort函数
    • 到第一次quicksort的第二个quicksort的第一个quicksort的第二个quicksort函数
    • 到第一次quicksort的第二个quicksort的第二个quicksort
    • 第一次quicksort的第二个quicksort执行完
    • 第一个quicksort执行完
  • 算法效率分析
    • 最好的情况
    • 最坏的情况
    • 优化
    • 算法效率小结
  • 稳定性
  • 小结

总览

在这里插入图片描述

快速排序（超级重要）

啥是快速排序

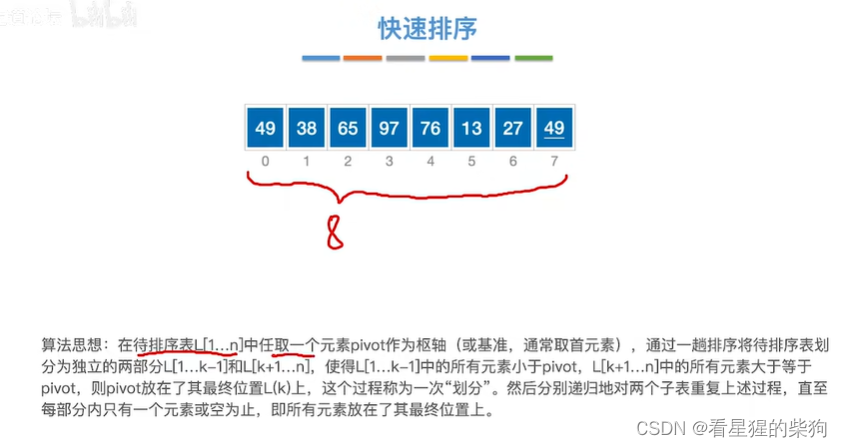
在这里插入图片描述

演示过程

此时选49为枢轴元素，接着low和high往中间移动，并且保证，low左边都是小于枢轴元素，high元素右边都是大于枢轴元素
此时high位置的49大于等于49，high左移
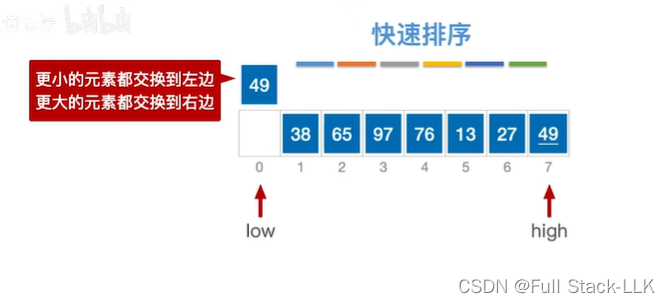
在这里插入图片描述
此时high所指的元素为27小于49，所以将high位置的元素移动到low位置
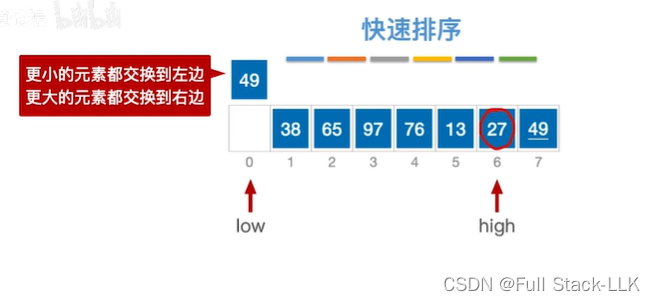
在这里插入图片描述
移动后，high的位置空出来，此时移动low位置，此时low的位置的元素为27，小于49，low移动在这里插入图片描述
此时low位置的元素依然小于49，low移动
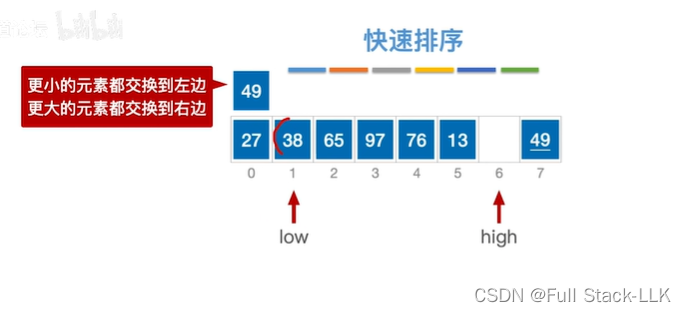
在这里插入图片描述
此时low指向的元素65大于49，移动到high位置
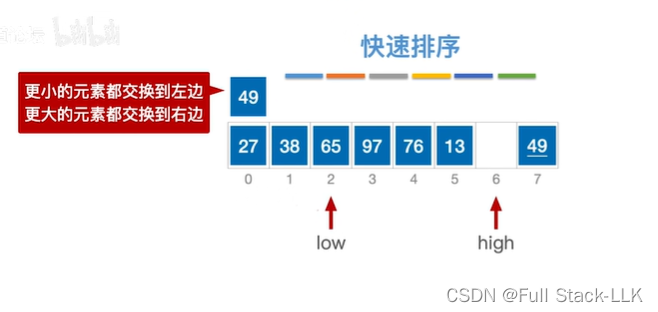
在这里插入图片描述
此时low位置空了，移动high位置，此时high位置的元素大于49，high左移
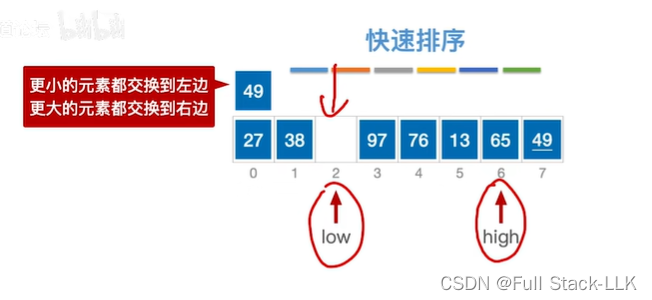
在这里插入图片描述
此时high位置元素13小于49，13移动到low位置，
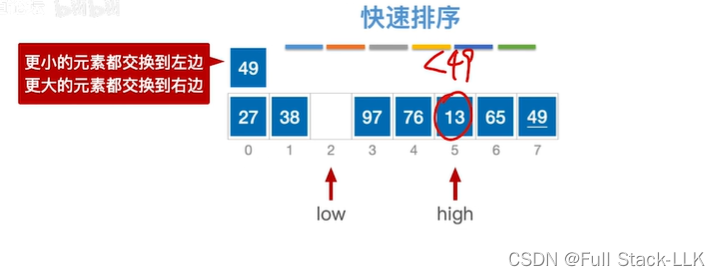
在这里插入图片描述
此时high空，移动low，此时13小于49，low右移
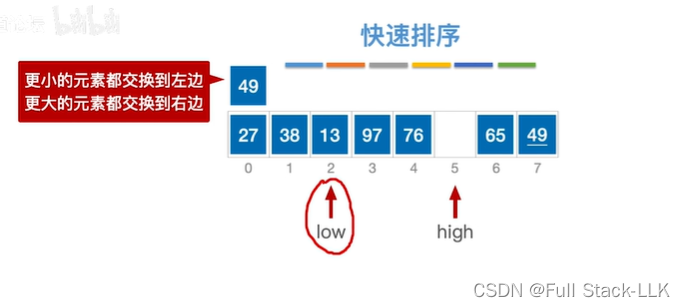
在这里插入图片描述
此时97大于49，将97移动到high

在这里插入图片描述
此时移动high，97大于49，high左移
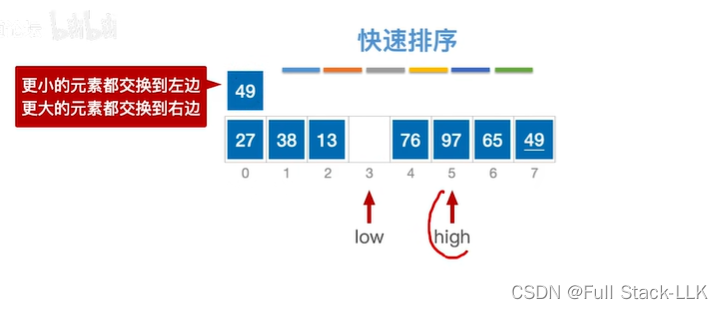
在这里插入图片描述
此时76大于49，high左移
在这里插入图片描述
low和high碰到一起，此时左右元素都扫了一遍了，比49都小的元素都放到low的左边了，比49大的元素都放high的右边，
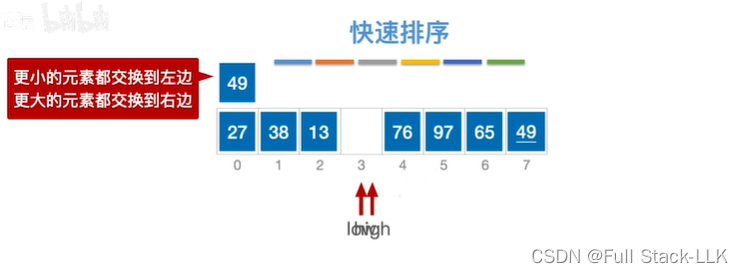
在这里插入图片描述
然后把枢轴元素放到low和high重合的位置
在这里插入图片描述

接下来对分别对左右两个子表进行刚刚的过程
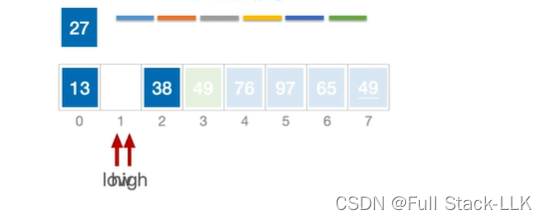
此时是左子表，high位置元素13小于27，移动到low
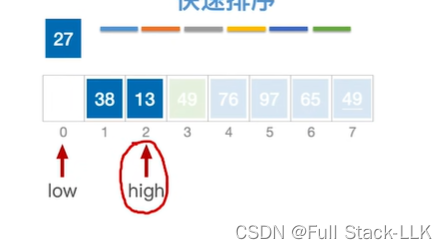
在这里插入图片描述
此时移动low，13小于27，low右移，
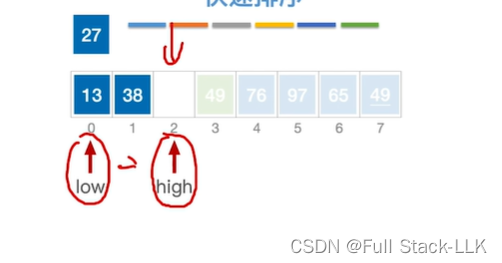
在这里插入图片描述
此时38大于27，38移到high
在这里插入图片描述
此时移动high，38大于27，high左移
在这里插入图片描述
此时high和low重合，27放入该位置
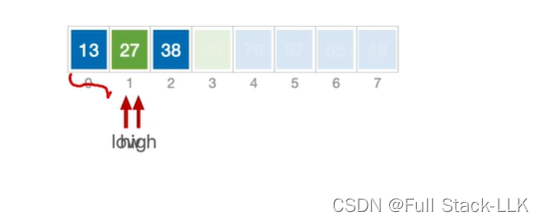
在这里插入图片描述
此时该子表又划分两个子表，此时两个子表都只有一个元素，此时不需要处理，因为此时low左边元素小于枢轴，high右边元素大于枢轴，又因为此时左右都只有一个元素，所以已经有序
在这里插入图片描述
此时要处理右子表，high所指元素49小于76，49移动到low，
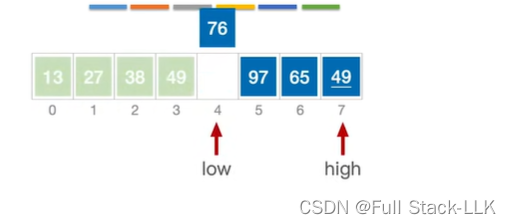
在这里插入图片描述
此时49小于76,low右移动
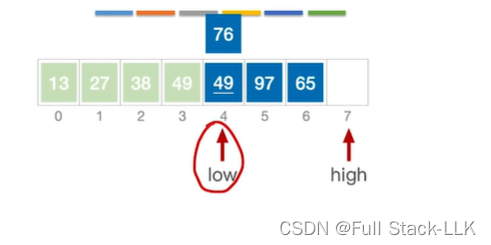
在这里插入图片描述
此时97大于76，97移动到high
在这里插入图片描述
此时high移动，97大于76，high左移
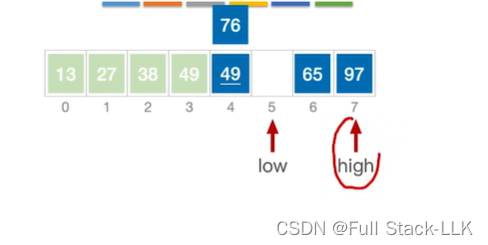
在这里插入图片描述
65小于76，65移动到low
在这里插入图片描述
low移动，65小于76，low右移，
在这里插入图片描述
low和high碰头，76放入该位置
在这里插入图片描述
此时再次划分为两个子表，对左子表处理
此时65大于49，high左移

在这里插入图片描述
low和high碰头，49放该位置

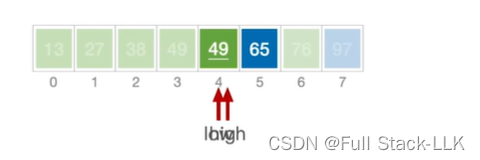
在这里插入图片描述
此时由于65和97都只有一个元素，所以直接确定位置
最后排序结果
在这里插入图片描述

算法实现

在这里插入图片描述

首先调用QuickSor函数，开始对整个表划分，并调用partition函数，此时划分整个表

第一次quicksort函数

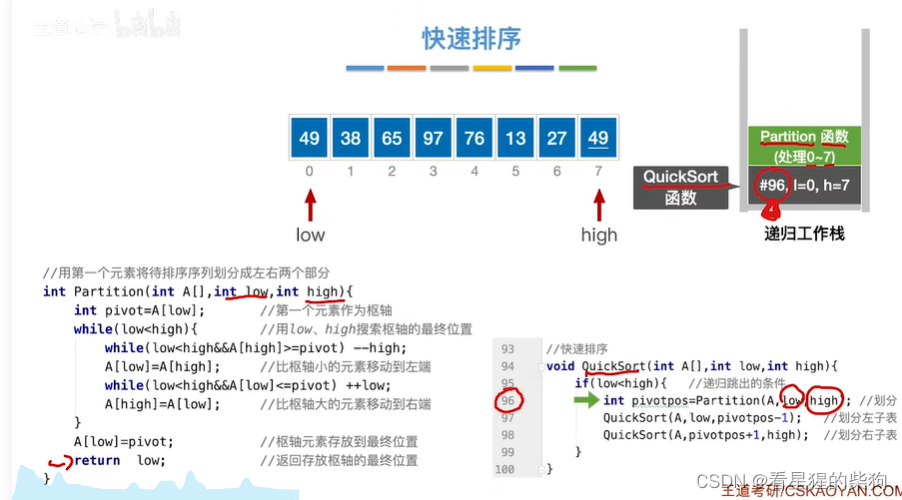
在这里插入图片描述

第一次partion函数

pivot就是枢轴的意思
此时partion函数大循环的条件是low<high，当low=high时将停止循环
此时大循环中还有两个循环，先是high位置开始的循环，然后是low开始的循环
发现49大于要枢轴值
high左移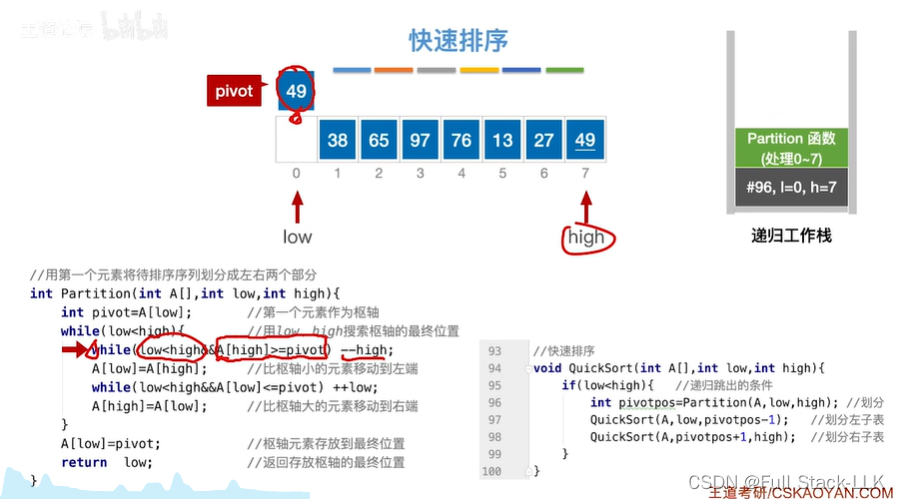在这里插入图片描述
此时27小于枢轴值
跳出while循环，并将此时的high的值赋值给low位置
在这里插入图片描述
此时跳到下一个while循环，比较low位置的值和枢轴的值，如果low的值小于枢轴的值，此时low往后移动
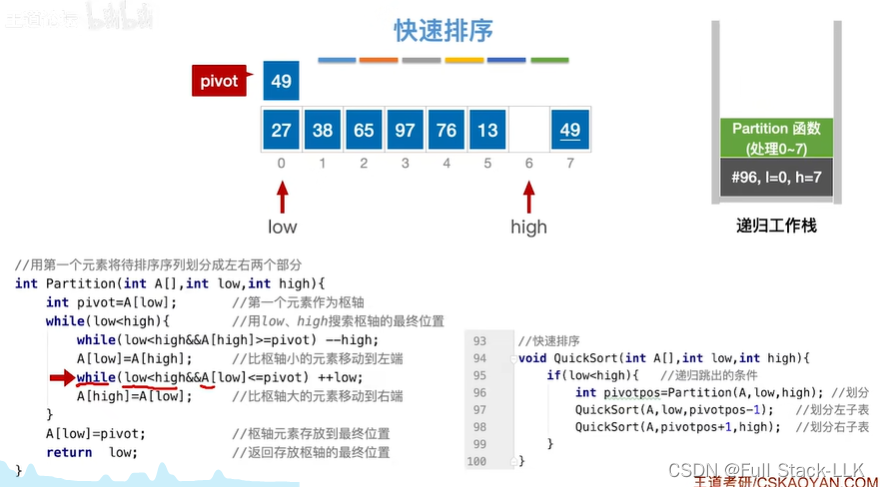
在这里插入图片描述
此时直到65发现low的值大于枢轴的值，跳出循环
此时移动low位置的值到high位置上去，此时回到大循环，发现low<high，继续下一次大循环，但大循环仍然是在溢依次分表之中
在这里插入图片描述
此时继续开始第一次小循环，到13跳出第一次小循环，并将high位置的值给low位置的值

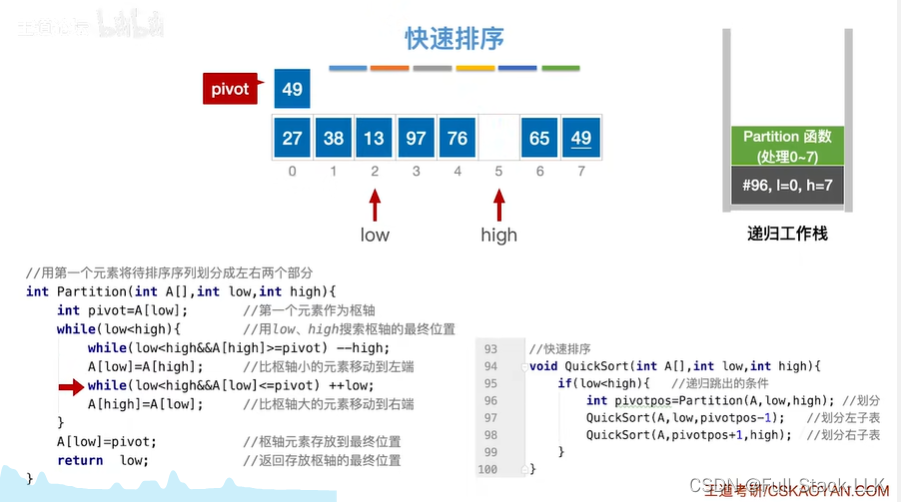
在这里插入图片描述
此时开始第二次小循环，到97跳出第二次小循环，并将low值给high位置的值，然后进入下次大循环
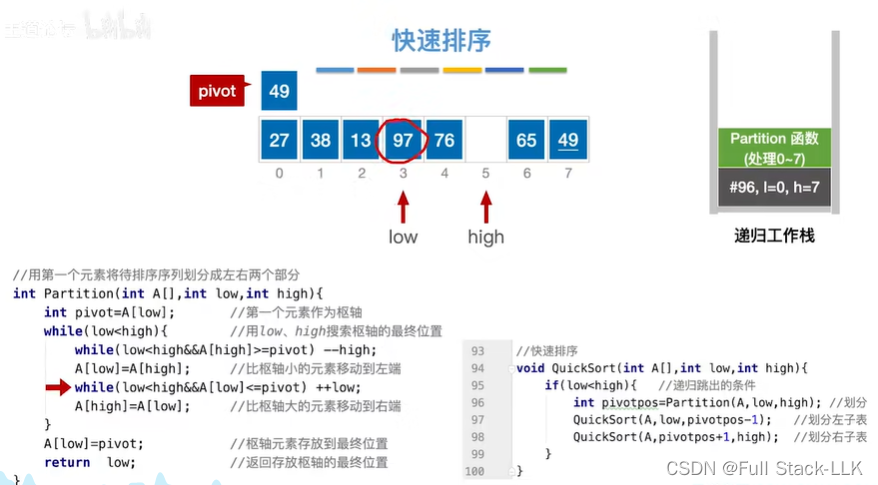
在这里插入图片描述
此时进入第一次小循环，此时当high移动到与low相同才跳出第一次小循环，此时由于low=high，第二次小循环也会跳出，随后大循环条件不满足了，跳出大循环
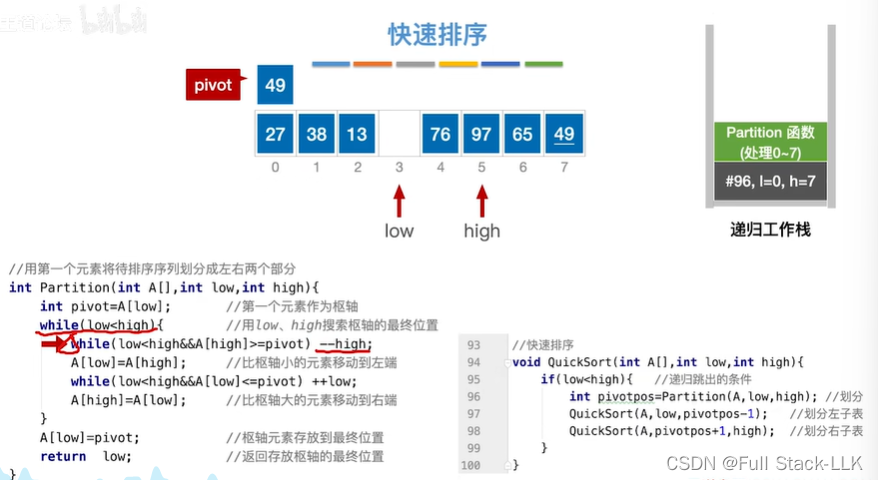
在这里插入图片描述
然后将枢轴元素放到low的位置，并return low的值那么就完成了一次划分的工作
此时quicksort函数中pivotpos的值为该次划分的枢轴的位置
在这里插入图片描述

到第一次quicksort的第一个quicksort

此时处理之前划分的左子表，从low到之前返回得到的枢轴的位置
在这里插入图片描述
此时函数执行过程与之前类似，此时partition函数返回27，返回到第二次quicksort函数中
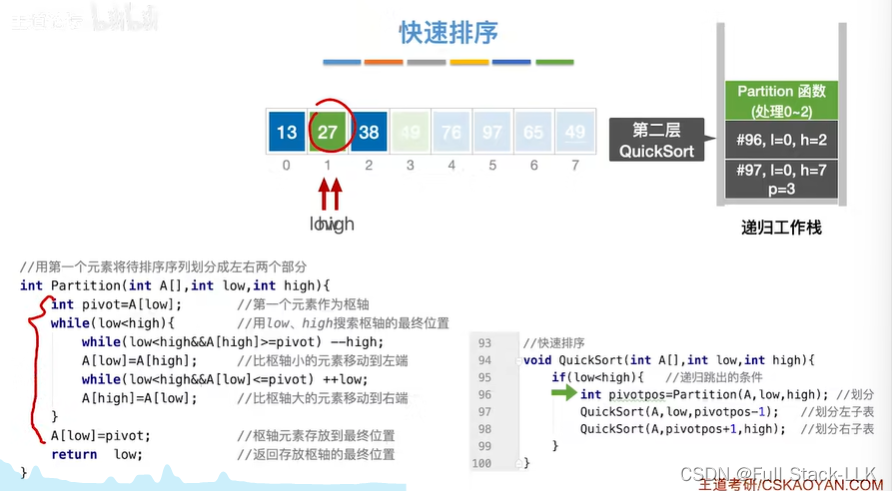
在这里插入图片描述

到第二次quicksort的第一个quicksort

此时的low和high相等，直接跳出if语句
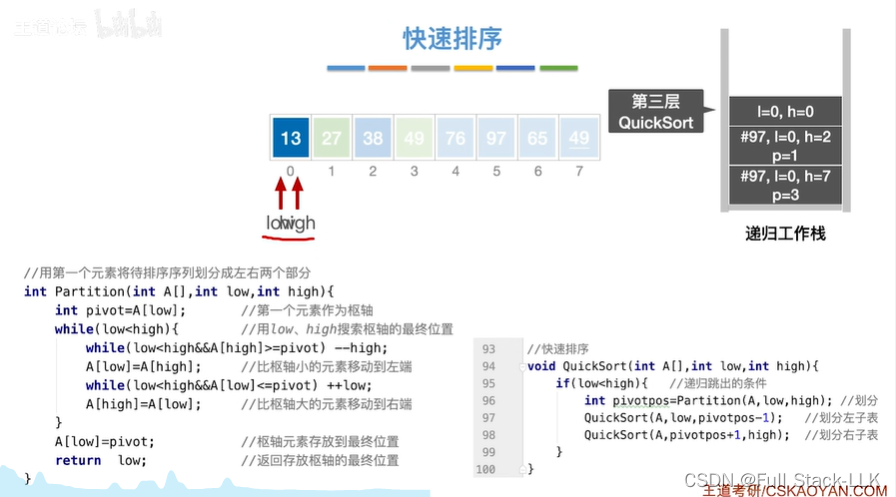
在这里插入图片描述

到第二次quicksort的第二个quicksort

此时low依然等于high，直接跳出if

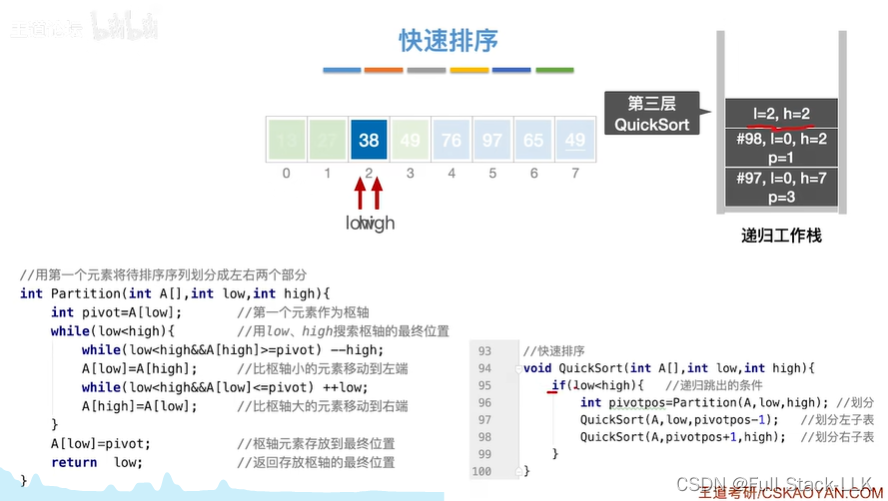
在这里插入图片描述

到第一次quicksort的第二个quicksort

此时low=3+1=4，high=7
在这里插入图片描述

到第一次quicksort的第二个quicksort的partition

执行过程于之前相同
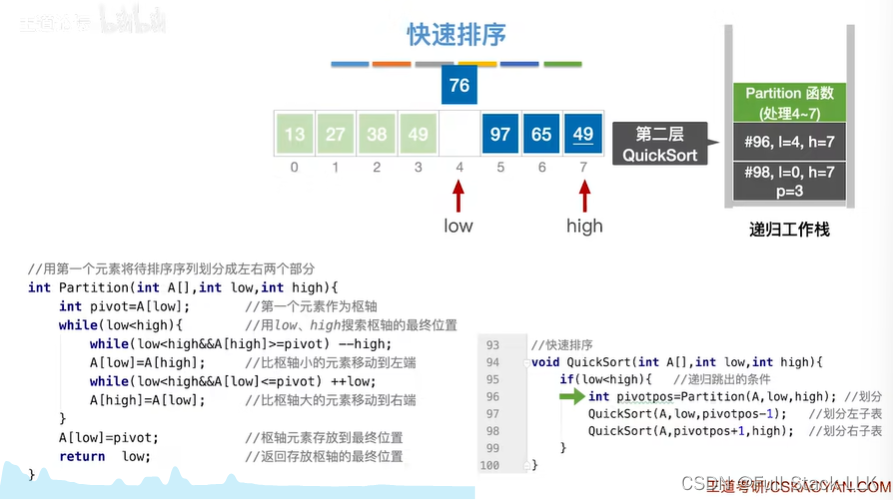
在这里插入图片描述
结果
在这里插入图片描述

到第一次quicksort的第二个quicksort的第一个quicksort

此时之前的partition返回到pivotpos为6
此时的quicksort处理的low为4，high为6-1=5
在这里插入图片描述

到第一次quicksort的第二个quicksort的第一个quicksort的partition函数

此时结果
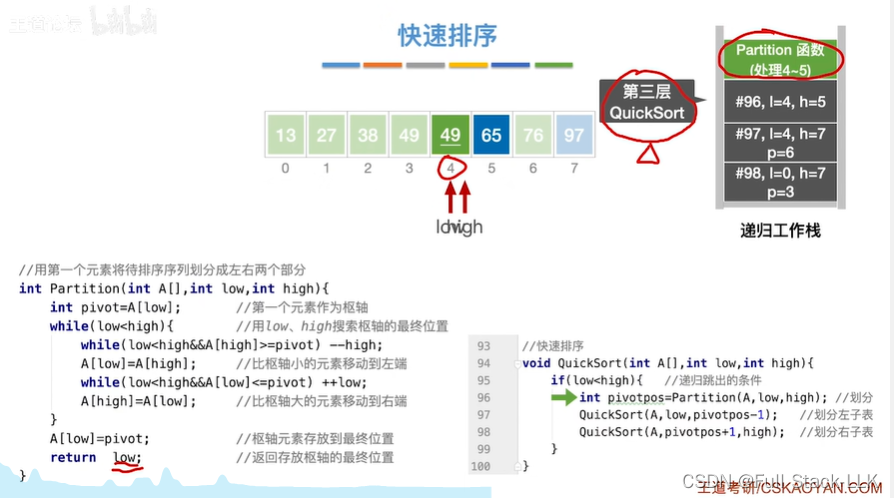
在这里插入图片描述

到第一次quicksort的第二个quicksort的第一个quicksort的第一个quicksort函数

此时之前的partition返回的pivotpos为4
则第一个quicksort对呀的low和4，high为4-1=3
此时不满足low<high，跳出if语句
在这里插入图片描述

到第一次quicksort的第二个quicksort的第一个quicksort的第二个quicksort函数

此时low=4+1=5，high=5，不满足low<high，跳出if语句
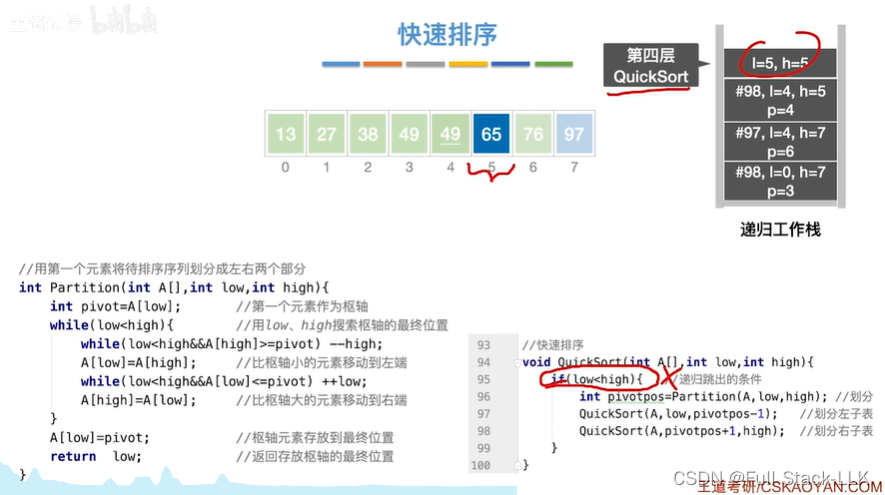
在这里插入图片描述

到第一次quicksort的第二个quicksort的第二个quicksort

此时low=6+1=7，high=7，同样不满足low<high,会跳出if
在这里插入图片描述

第一次quicksort的第二个quicksort执行完

在这里插入图片描述

第一个quicksort执行完

排序完成
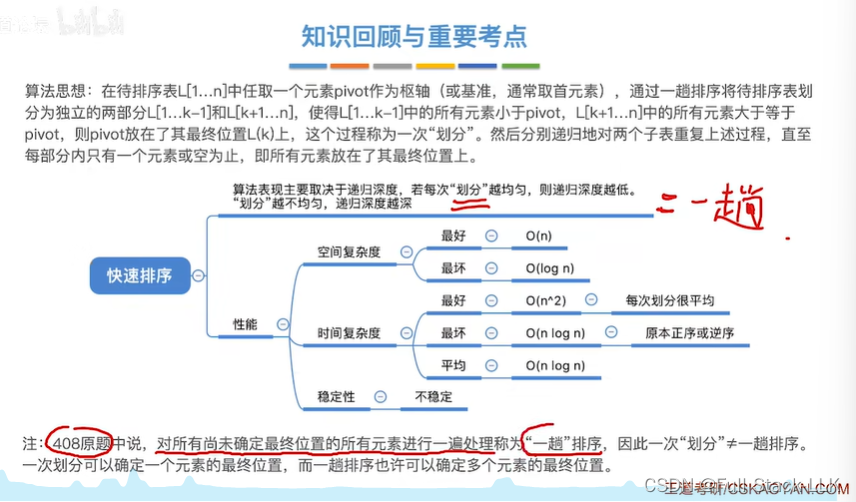
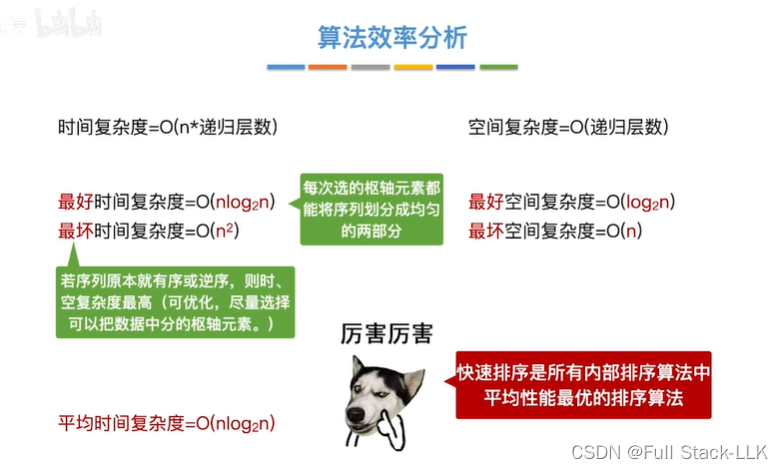
在这里插入图片描述

算法效率分析

函数每次先得到该范围的枢轴的位置，然后再以该枢轴为中级元素分开两个范围，对各个范围进行函数

partion函数需要通过low和high将该范围的数据都遍历一遍，因为终止条件是low=high
在这里插入图片描述
此时空间复杂度为调用过程中调用函数栈最多的时候
在这里插入图片描述
每层quicksort都是上一层quicksort分成的子表处理，每层处理都分成两个子表在这里插入图片描述
递归层数就是二叉树的层数
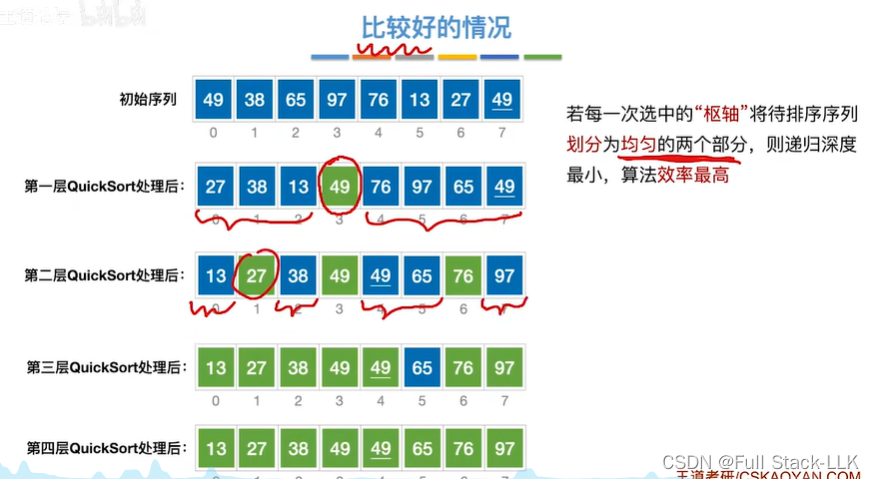
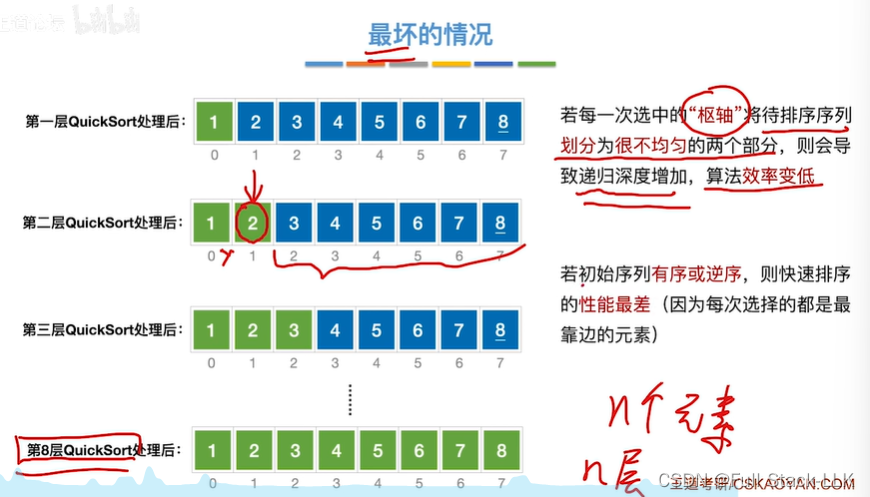
在这里插入图片描述

最好的情况

在这里插入图片描述

最坏的情况

在这里插入图片描述
此时high需要左移low才行，第一层quicksort处理后，第二层只需对右边部分处理
在这里插入图片描述
此时依然high需要移到low
在这里插入图片描述
第二层处理后，第三层只需对右边部分处理
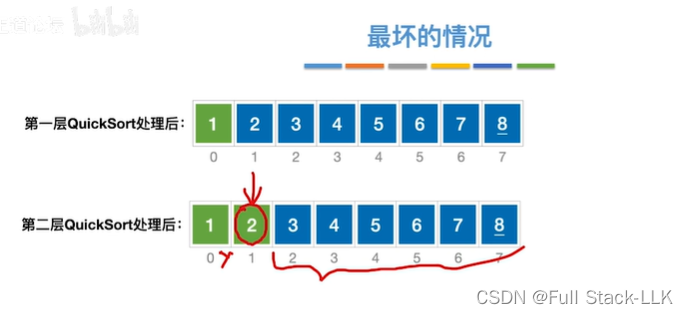
在这里插入图片描述
按照这样，需要8层quicksort调用
如果是逆序，第一层quicksort后，ow移动到最右边的位置即high位置，第二层都只需要处理左边部分，，之后的处理类似
在这里插入图片描述

优化

即让枢轴的值极可能不要是最大值或最小值
在这里插入图片描述

算法效率小结

实际情况实际复杂度都接近于最好时间复杂度
在这里插入图片描述

稳定性

看这个例子
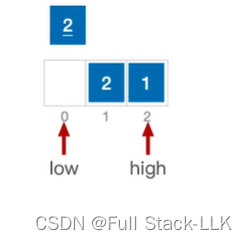
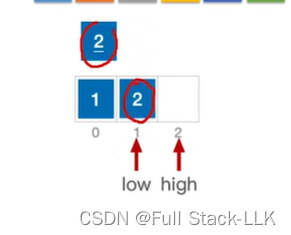
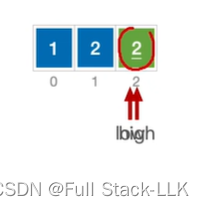
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
是不稳定的
在这里插入图片描述

小结

下图时间复杂度最好和最坏写反了
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1362769.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

UnityVR入门之六 如何让3DUI层级在场景模型之上

UnityVR入门之六 如何让3DUI层级在场景模型之上

一、问题来源 根据 UnityVR入门之五 射线检测交互-CSDN博客 这一章节我们了解到VR要与UI交互需要将Canvas设置为World Space属性&#xff0c;然后使用碰撞盒的方式进行射线交互。 正常我们ui是始终叠加在3d场景之上的&#xff0c;如此设置当ui与场景模型相交就会遮挡穿模 二、解…
阅读更多...
【Java集合篇】负载因子和容量的关系

【Java集合篇】负载因子和容量的关系

负载因子和容量有什么关系 ✔️典型解析✔️loadfactor为啥默认是0.75F&#xff0c;不是1呢?✔️为什么HashMap的默认负载因子设置成0.75✔️0.75的数学依据是什么✔️0.75的必然因素 ✔️HashMap的初始值设为多少合适? ✔️典型解析 HashMap 中有几个属性&#xff0c;如 cap…
阅读更多...
使用qtquick调用python程序，pytorch

使用qtquick调用python程序，pytorch

一. 内容简介 使用qtquick调用python程序 二. 软件环境 2.1vsCode 2.2Anaconda version: conda 22.9.0 2.3pytorch 安装pytorch(http://t.csdnimg.cn/GVP23) 2.4QT 5.14.1 新版QT6.4,&#xff0c;6.5在线安装经常失败&#xff0c;而5.9版本又无法编译64位程序&#xf…
阅读更多...
云尚办公项目学习

云尚办公项目学习

完整的笔记可以参考这个专栏&#xff0c;写的挺详细的&#xff1a;云尚办公课件笔记&#xff0c;come on boy 文章目录 form-create表设计步骤1&#xff0c;创建审批类型2&#xff0c;创建审批类型下的审批模板3&#xff0c;为指定的审批模板设置模板名称&#xff0c;表单项&am…
阅读更多...
Python笔记01-你好Python

Python笔记01-你好Python

文章目录 Python简介环境安装Hello world开发工具 Python简介 python的诞生 1989年&#xff0c;为了打发圣诞节假期&#xff0c;Gudio van Rossum吉多 范罗苏姆&#xff08;龟叔&#xff09;决心开发一个新的解释程序&#xff08;Python雏形&#xff09; 1991年&#xff0c;第…
阅读更多...
CSS 压重按钮 效果

CSS 压重按钮 效果

<template><view class="cont"><div class="container"><div class="pane"><!-- 选项1 --><label class="label" @click="handleOptionClick(0)":style="{ color: selectedOption ==…
阅读更多...
【机器学习】循环神经网络（二）-LSTM示例（keras）国际航空乘客问题的回归问题...

【机器学习】循环神经网络（二）-LSTM示例（keras）国际航空乘客问题的回归问题...

使用 Keras 在 Python 中使用 LSTM 循环神经网络进行时间序列预测 国际航空乘客问题的回归问题 这个文件是一个CSV格式的数据集&#xff0c;它包含了从1949年1月到1960年12月的每个月的国际航空乘客的总数&#xff08;以千为单位&#xff09;。第一行是列名&#xff0c;分别是&…
阅读更多...
Open CASCADE学习|入门Hello world

Open CASCADE学习|入门Hello world

目录 1、新建项目 2、写代码 3、配置 3.1配置头文件 3.2配置静态库文件 3.3配置动态库文件 4、编译运行 1、新建项目 新建一个Win32控制台应用程序&#xff0c;取名为HelloWorld&#xff0c;如下图所示&#xff1a; 2、写代码 测试所用的代码如下&#xff1a; // Use T…
阅读更多...
数据分析基础之《numpy（6）—IO操作与数据处理》

数据分析基础之《numpy（6）—IO操作与数据处理》

了解即可&#xff0c;用panads 一、numpy读取 1、问题 大多数数据并不是我们自己构造的&#xff0c;而是存在文件当中&#xff0c;需要我们用工具获取 但是numpy其实并不适合用来读取和处理数据&#xff0c;因此我们这里了解相关API&#xff0c;以及numpy不方便的地方即可 2…
阅读更多...
Rockchip平台双屏异显功能实现(基于Android13)

Rockchip平台双屏异显功能实现(基于Android13)

Rockchip平台双屏异显功能实现(基于Android13) 1. 异显实现方案 Rockchip SDK平台支持两种不同的异显方案&#xff1a;Android Presentation和Android Activity指定屏幕启动。 使用Android Presentation方案&#xff0c;需要在APP开发中调用相应接口以使指定视图&#xff08…
阅读更多...
ATTCK视角下的信息收集：主机发现

ATTCK视角下的信息收集：主机发现

目录 1、利用协议主动探测主机存活 利用ICMP发现主机 利用ARP发现主机 利用NetBIOS协议发现主机 利用TCP/UDP发现主机 利用DNS协议发现主机 利用PRC协议发现主机程序 2、被动主机存活检测 利用Browser主机探测存活主机 利用ip段探测主机存活 利用net命令探测主机存活…
阅读更多...
论文笔记 Understanding Electricity-Theft Behavior via Multi-Source Data

论文笔记 Understanding Electricity-Theft Behavior via Multi-Source Data

WWW 2020 oral 1 INTRO 1.1 背景 1.1.1 窃电 窃电&#xff08;electricity theft&#xff09;指用户为了逃避电费而进行非法操作的一种行为 常用的反窃电方法可分为两类&#xff1a; 基于硬件驱动的反窃电方法 ​​​​​​​电表开盖检测、集中器检测。。。。 硬件驱动的…
阅读更多...
18.标题统计

18.标题统计

题目 import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc new Scanner(System.in);String str sc.nextLine();int res 0;for(int i0;i<str.length();i) {char c str.charAt(i);if(c! && c!\n) {res;}}System.o…
阅读更多...
Simply主题 简约风格的Emlog博客模板 响应式布局

Simply主题 简约风格的Emlog博客模板 响应式布局

主题介绍 Simply是一款简约风格的Emlog博客模板&#xff0c;响应式布局、界面简单大方&#xff0c;实用性强&#xff01; 支持夜间模式&#xff0c;采用localStorage存储配置。IOS系统下支持随系统自动切换浅/深色模式。 文章页支持显示文章字数及阅读时间。 支持http/https …
阅读更多...
MCS-51单片机的基本结构

MCS-51单片机的基本结构

目录 一.单片机的逻辑结构 1.单片机的基本结构 2.引脚 3.中断系统 4.时钟电路 5.时序 6.典型指令的取指、执行时序 7.80C51中定时器/计数器 二.单片机的复位 三.程序的执行方式 1.单步执行方式 2.低功耗操作方式 3.EPROM编程和校验方式 首先补充一个知识点&#x…
阅读更多...
JVM工作原理与实战(八)：类加载器的分类

JVM工作原理与实战(八)：类加载器的分类

专栏导航 JVM工作原理与实战 RabbitMQ入门指南 从零开始了解大数据 目录 专栏导航 前言 一、类加载器介绍 二、类加载器的分类 1.Java代码实现的类加载器 2.Java虚拟机底层源码实现的类加载器 3.默认的类加载器层次&#xff08;JDK8及之前的版本&#xff09; 总结 前言…
阅读更多...
听GPT 讲Rust源代码--compiler(15)

听GPT 讲Rust源代码--compiler(15)

File: rust/compiler/rustc_arena/src/lib.rs 在Rust源代码中&#xff0c;rustc_arena/src/lib.rs文件定义了TypedArena&#xff0c;ArenaChunk&#xff0c;DroplessArena和Arena结构体&#xff0c;以及一些与内存分配和容器操作相关的函数。 cold_path<F: FnOnce,drop,new,…
阅读更多...
PHP在线sqlite转html表格小功能(sqlite2html)

PHP在线sqlite转html表格小功能(sqlite2html)

6KB PHP实现在线sqlite转html表格小功能(支持大文件上传,得到一表一文件) 可自定义&#xff1a;上传限制大小&#xff1b;支持后缀格式!下载格式位压缩包&#xff0c;内含一表一个html文件。 作用&#xff1a;程序员实用工具&#xff0c;上传sqlite数据得到html表格数据供本地…
阅读更多...
主流大语言模型从预训练到微调的技术原理

主流大语言模型从预训练到微调的技术原理

引言 本文设计的内容主要包含以下几个方面&#xff1a; 比较 LLaMA、ChatGLM、Falcon 等大语言模型的细节&#xff1a;tokenizer、位置编码、Layer Normalization、激活函数等。大语言模型的分布式训练技术&#xff1a;数据并行、张量模型并行、流水线并行、3D 并行、零冗余优…
阅读更多...
迁移数据mysql到clickhouse

迁移数据mysql到clickhouse

场景&#xff1a; 项目上需要将mysql表中数据迁移到clickhouse。 理论&#xff1a; 借助MaterializeMySQL 说明&#xff1a; 首先该方案实施需要启动mysql的binlog配置否则同步不了&#xff0c;尽管MaterializeMySQL官方说是在实验阶段&#xff0c;不应该在生产上使用&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023