在Numpy中，有一个专门用于生成符合正态分布的随机数函数：numpy.random.normal，本文我们梳理一下它的使用方法，在梳理前，需要先了解一下什么是正态分布。

1. 正态分布

正态分布（Normal Distribution）又称高斯分布（Gaussian Distribution）。记得以前这个函数是在大学概率论里才介绍的，现在它已经出现在了高中课本中…这个神奇的函数描绘了现实世界中绝大多数事物的分布形态，用通俗的话解释“正态分布”就是：一个群体在某种指标上，绝大部分个体会落在平均值附近，超过平均值太多或低于平均值太多的个体数量都很少。正态分布函数的发现也非常漫长和曲折，感兴趣的读者可以阅读一下此文：《从数理统计简史中看正态分布的历史由来》

在这个函数中，我们要重点记住它的两个变量，它们也是后面numpy.random.normal函数的两个重要参数：

• μ（读mu): 数据分布的中心点，就是均值(mean)
• σ (读sigma)：数据分布的标准差(Standard Deviation)，控制曲线的陡峭程度，σ越小，数据就相对集中，曲线就越陡峭，反之亦然。

正是这两个变量决定了正态分布函数曲线的形状：

• 不同的μ值（均值）决定了曲线不同的中心位置(μ从-5到5的曲线变化)：

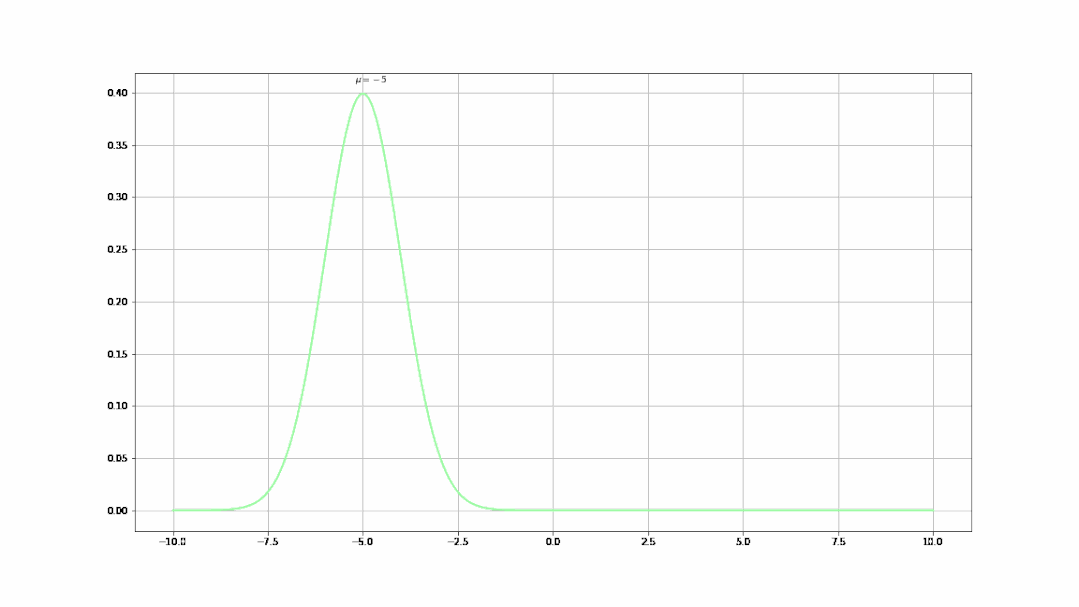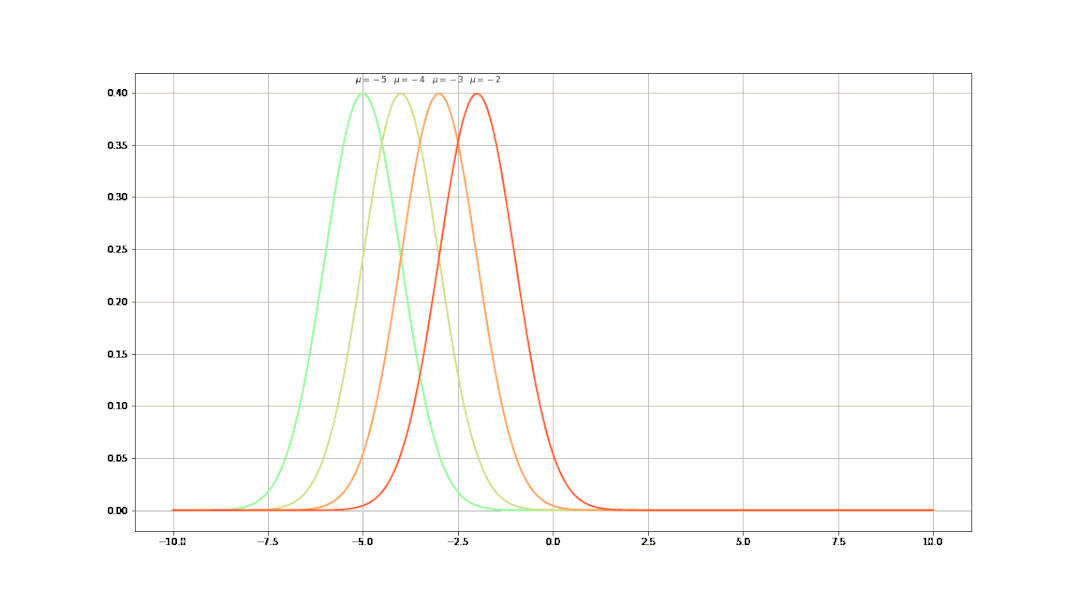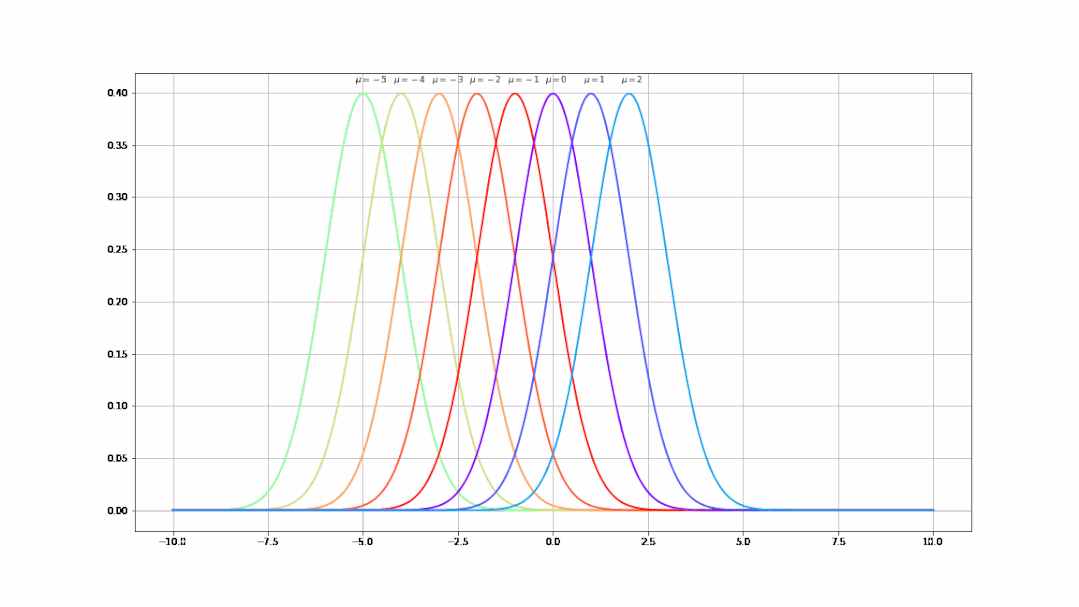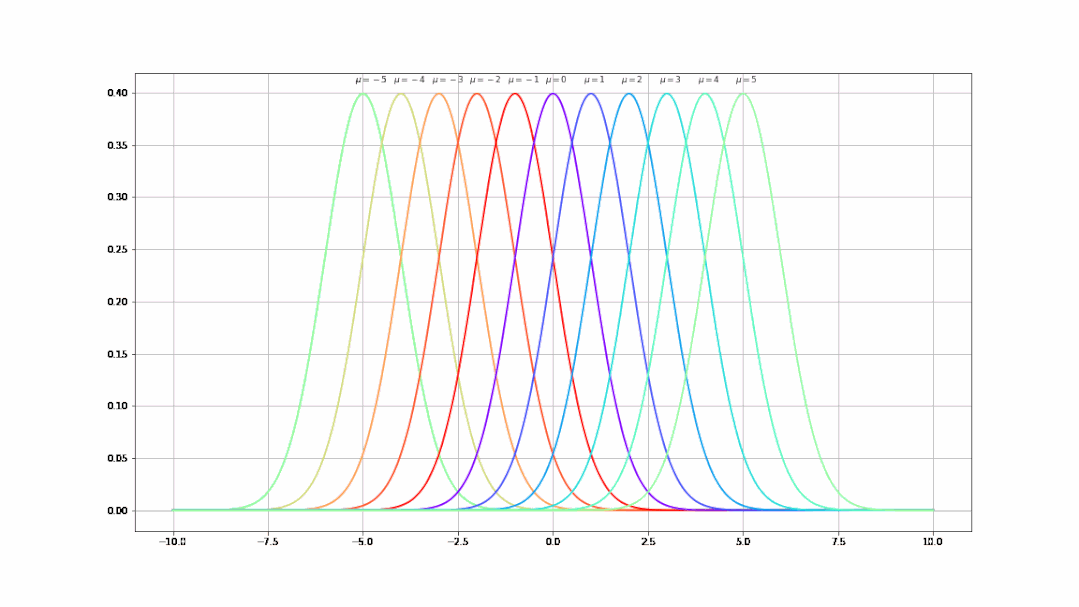
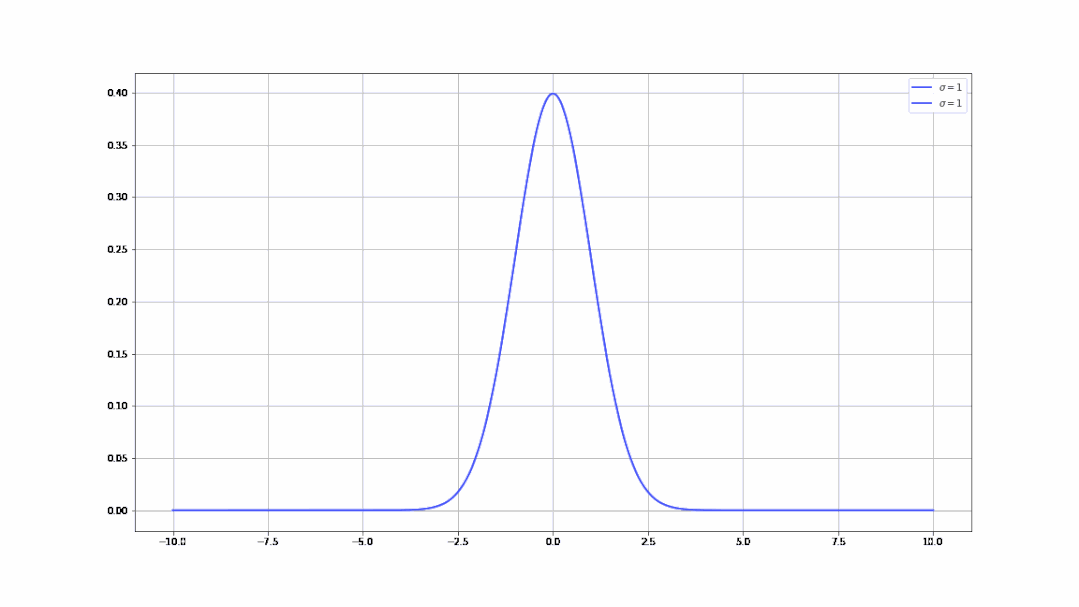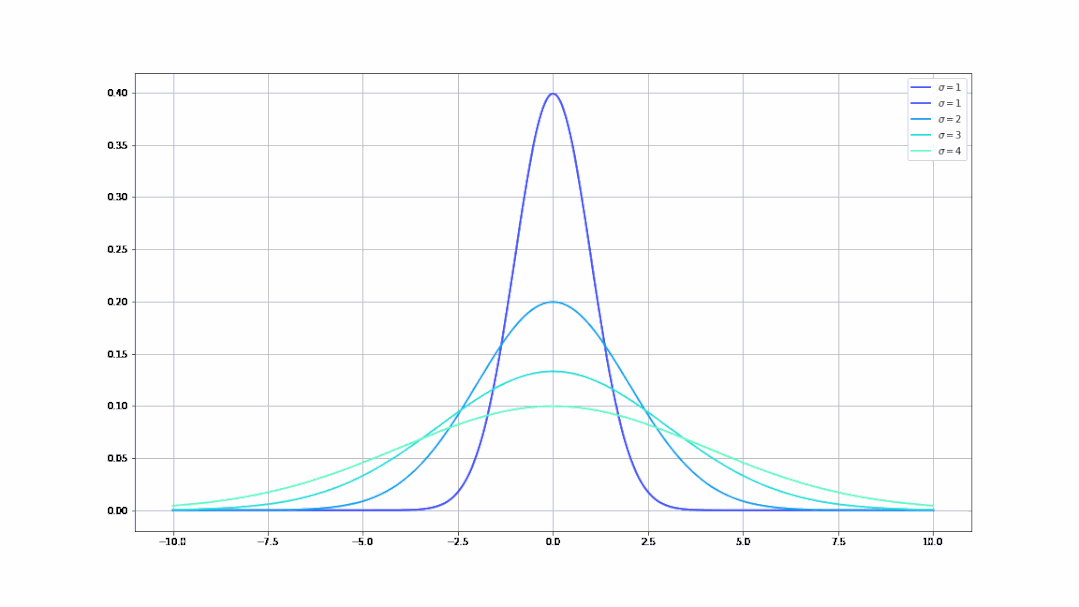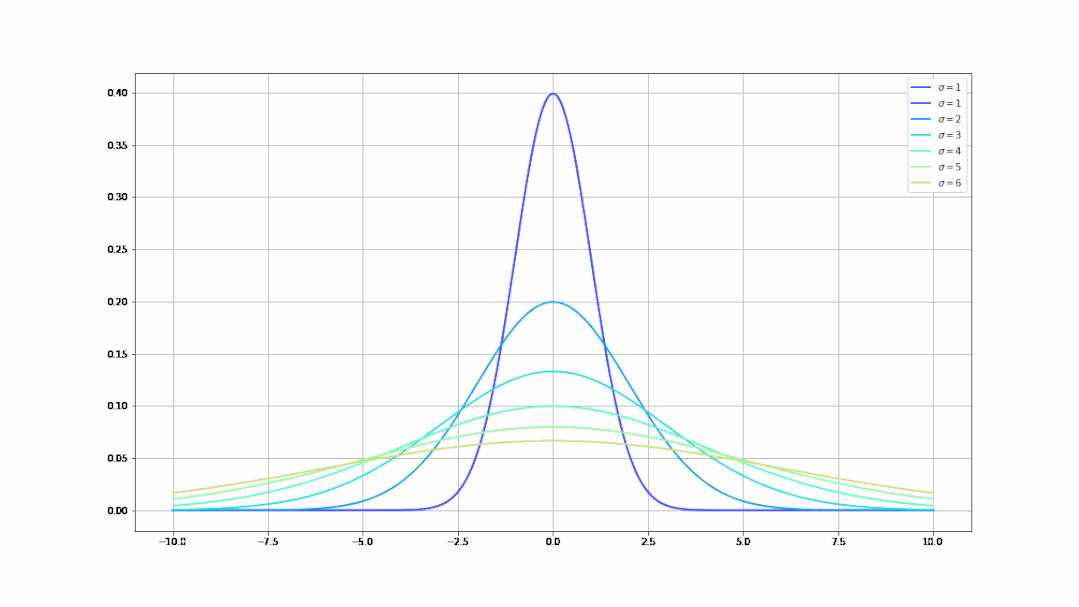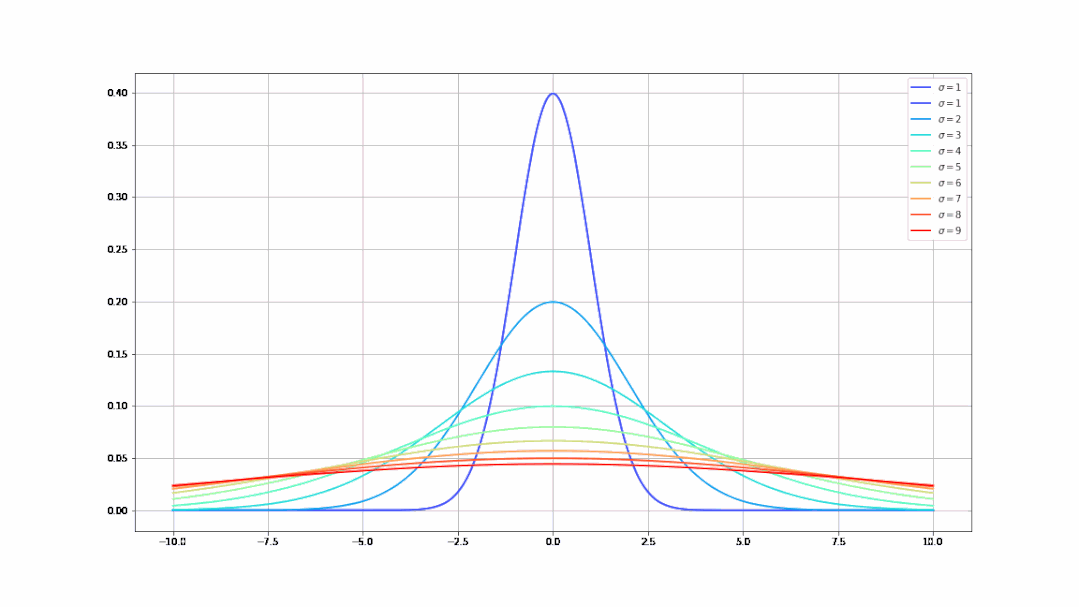
• 不同的σ值（均值）决定了曲线不同的陡峭程度（σ从1到9的曲线变化）：

2. numpy.random.normal函数

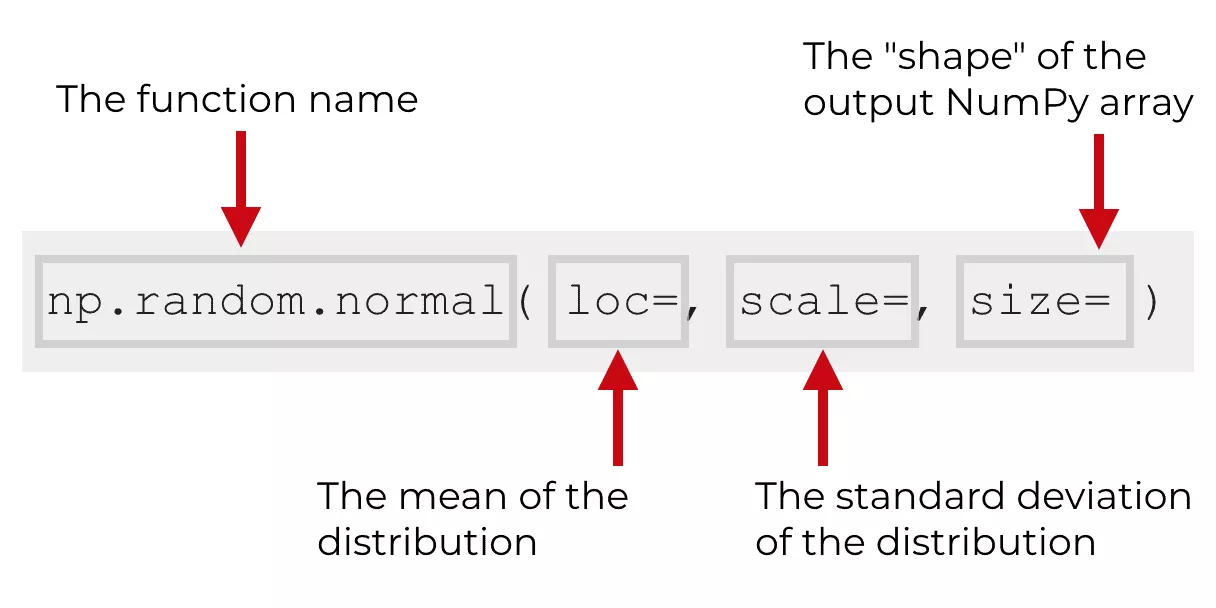
numpy.random.normal是numpy专门用于生成符合正态分布规律的随机数生成函数，它有三个最重要的参数：

• loc: 就是正态分布函数中的μ，即均值
• scale: 就是正态分布函数中的σ，即标准查
• size: 生成数据的数量

要特别提醒注意的是：这三个参数除了接受单一值之外，它们都可以接受元组或列表，这就意味着：我们利用该函数不仅仅能生成一维的随机数组，更能生成多维数组，每一个维度上的数据都符合正态分布。

3. 示例

在此前一篇文章《方差和标准差的意义》中，我们已经演示过numpy.random.normal函数的用法，且生成过一维的身高数据集和二组的体重和身高数据集，请参考该文的示例代码。

---

参考：

https://numpy.org/doc/stable/reference/random/generated/numpy.random.Generator.normal.html
https://www.sharpsightlabs.com/blog/numpy-random-normal/
https://mp.weixin.qq.com/s/PeM_jF5mdlkm9O6ZpDhVig