前端数据结构与算法
文章宝典
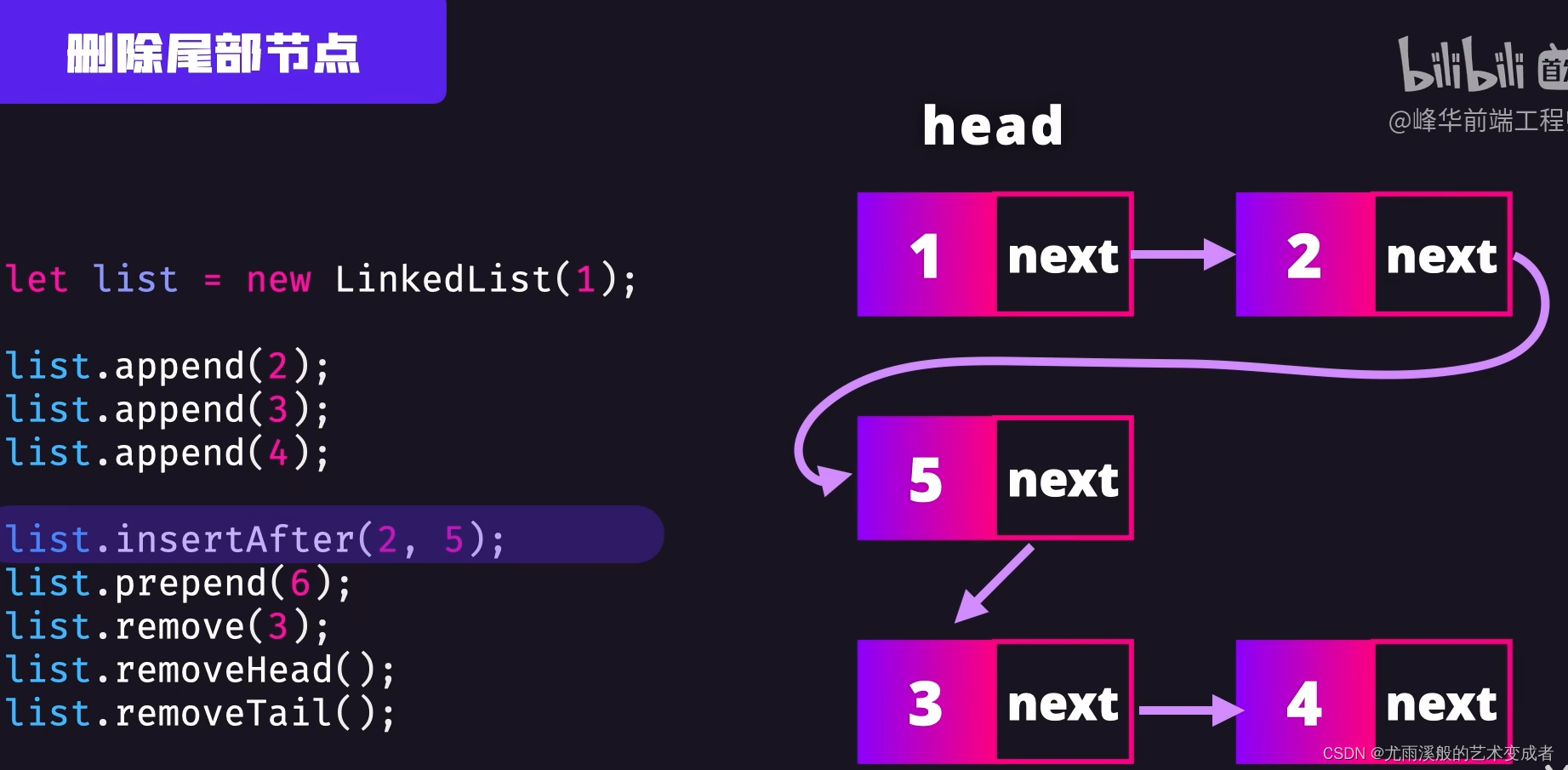
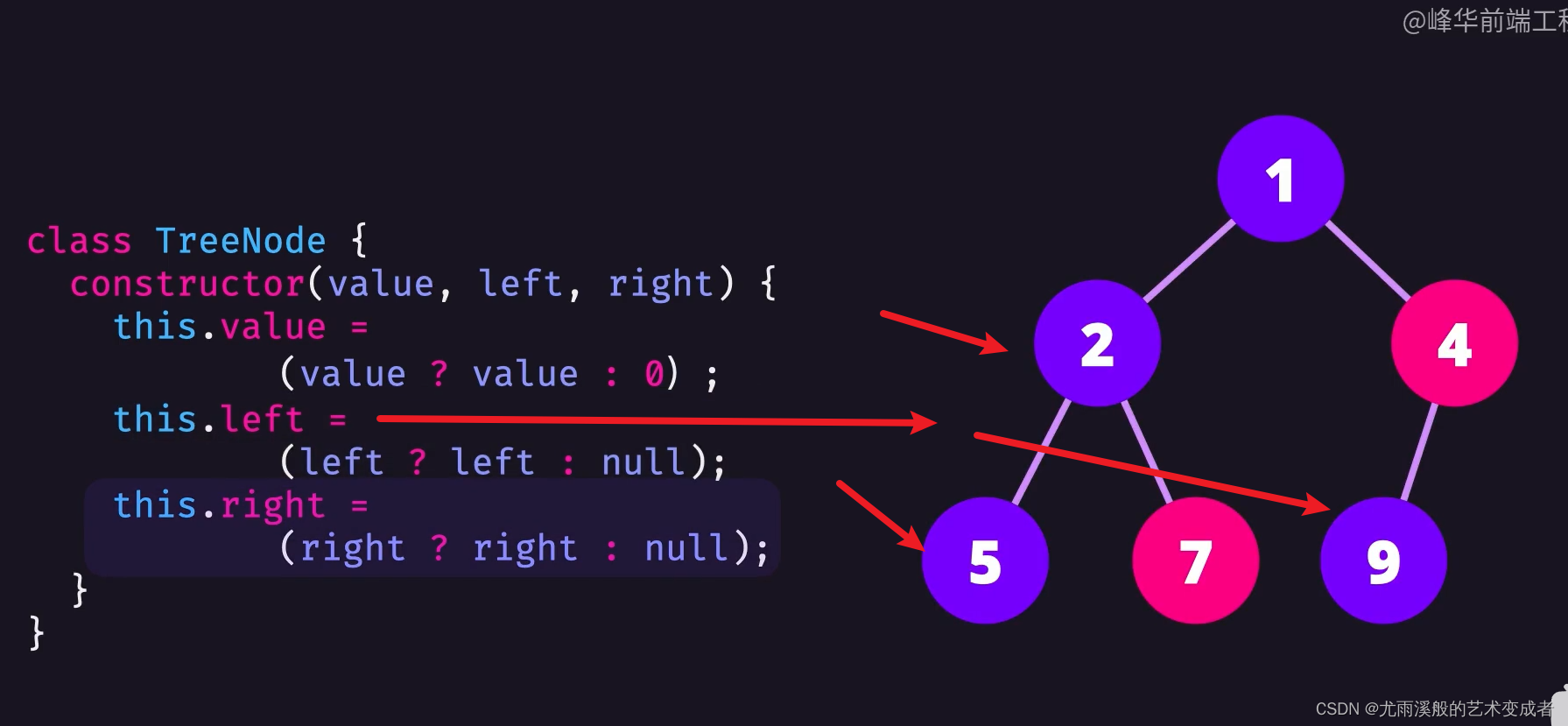
链表
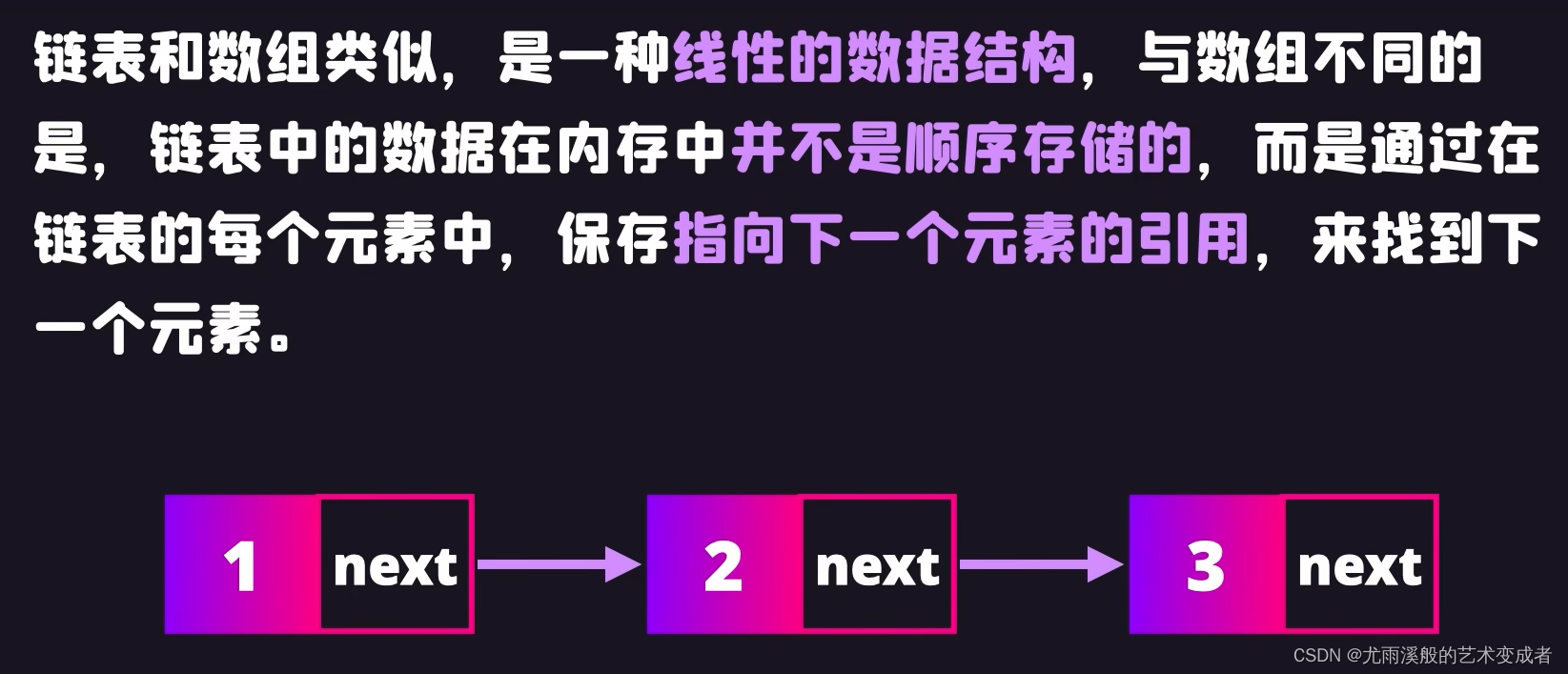


可以快速删除和插入节点,只用修改节点的引用


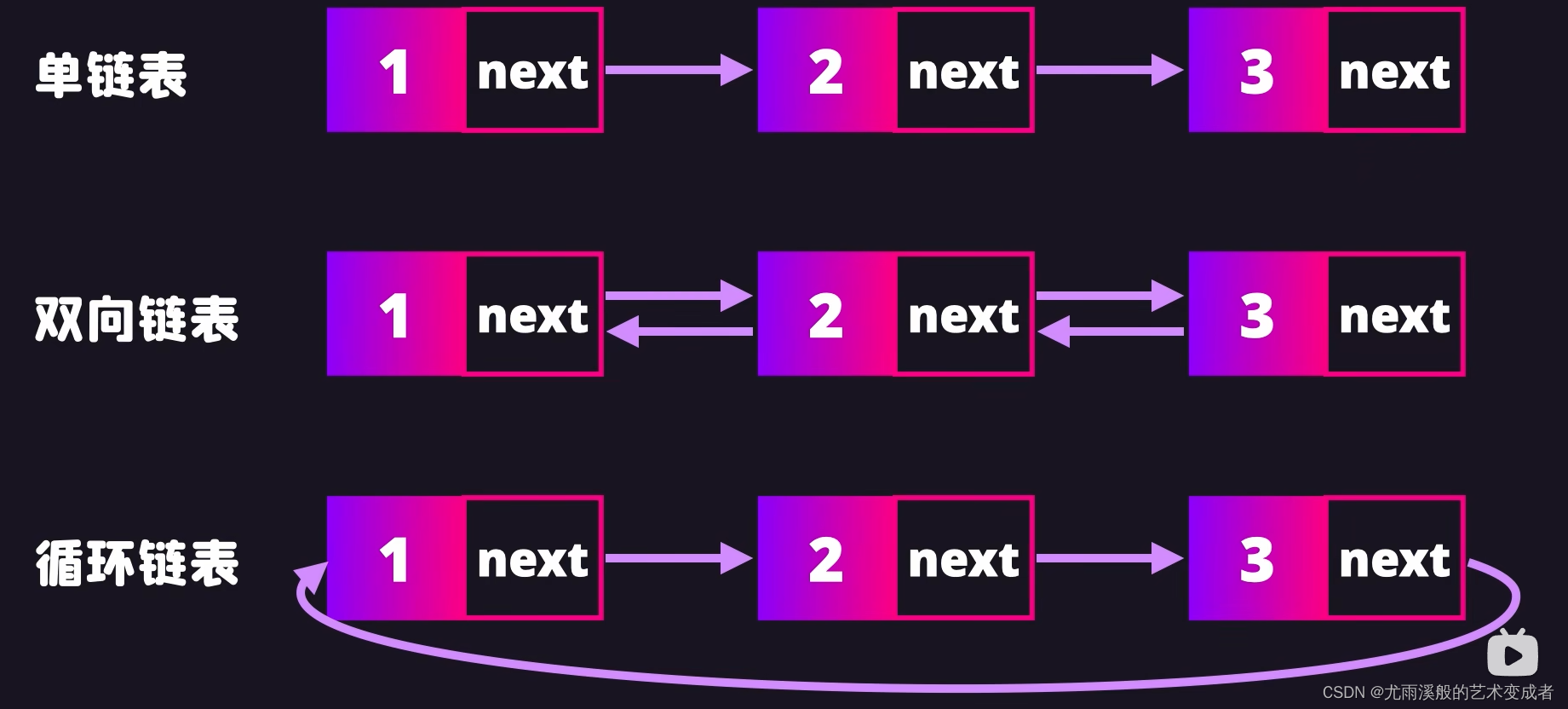
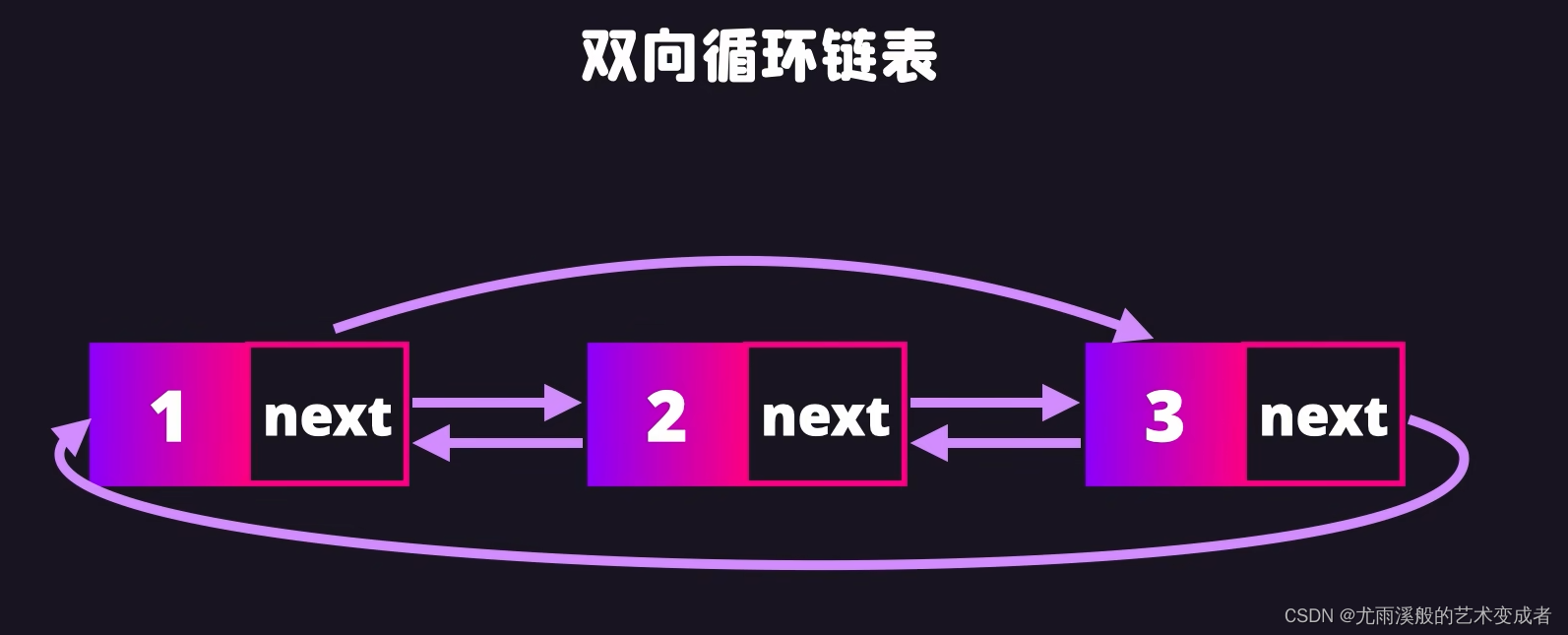

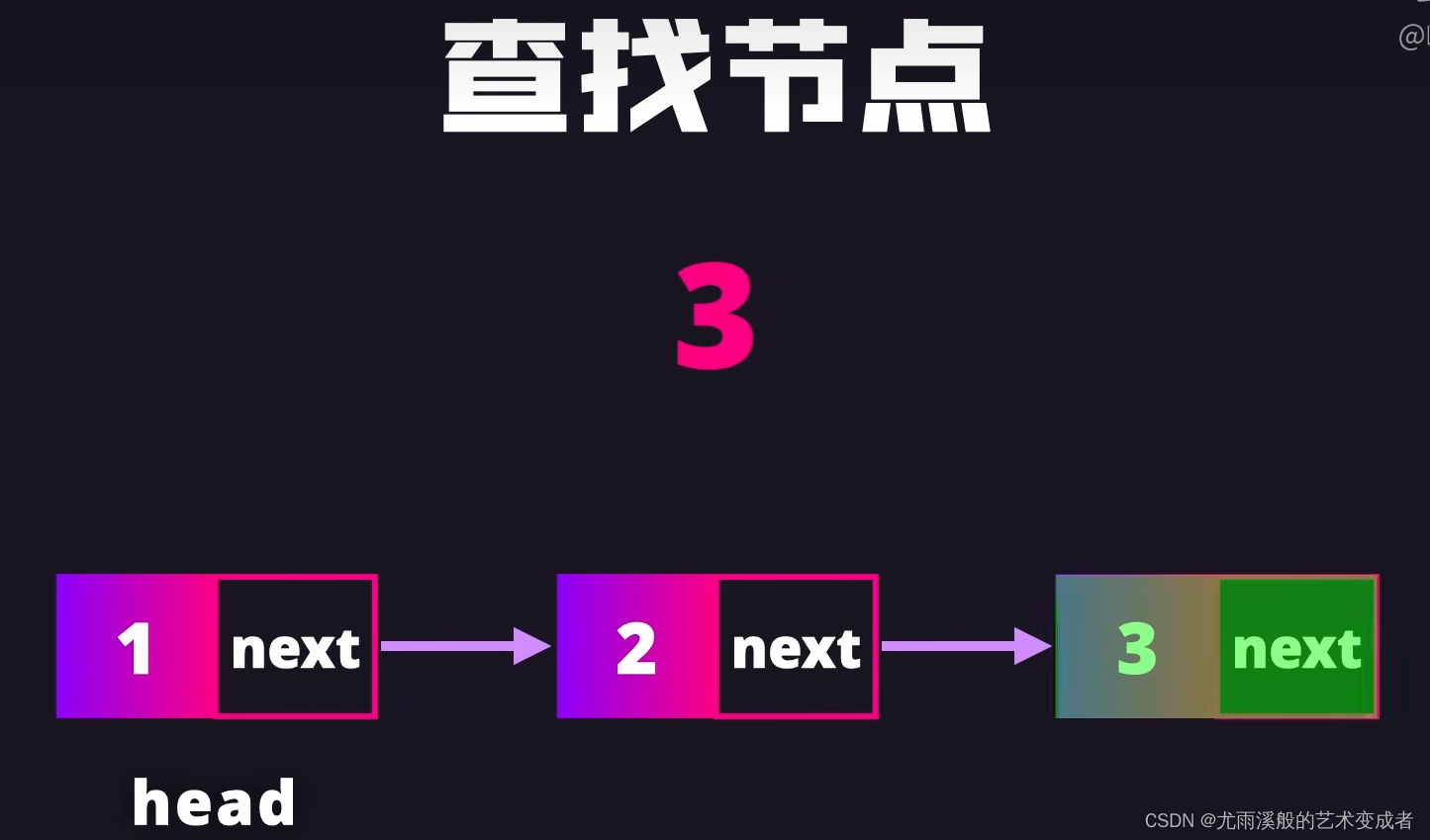
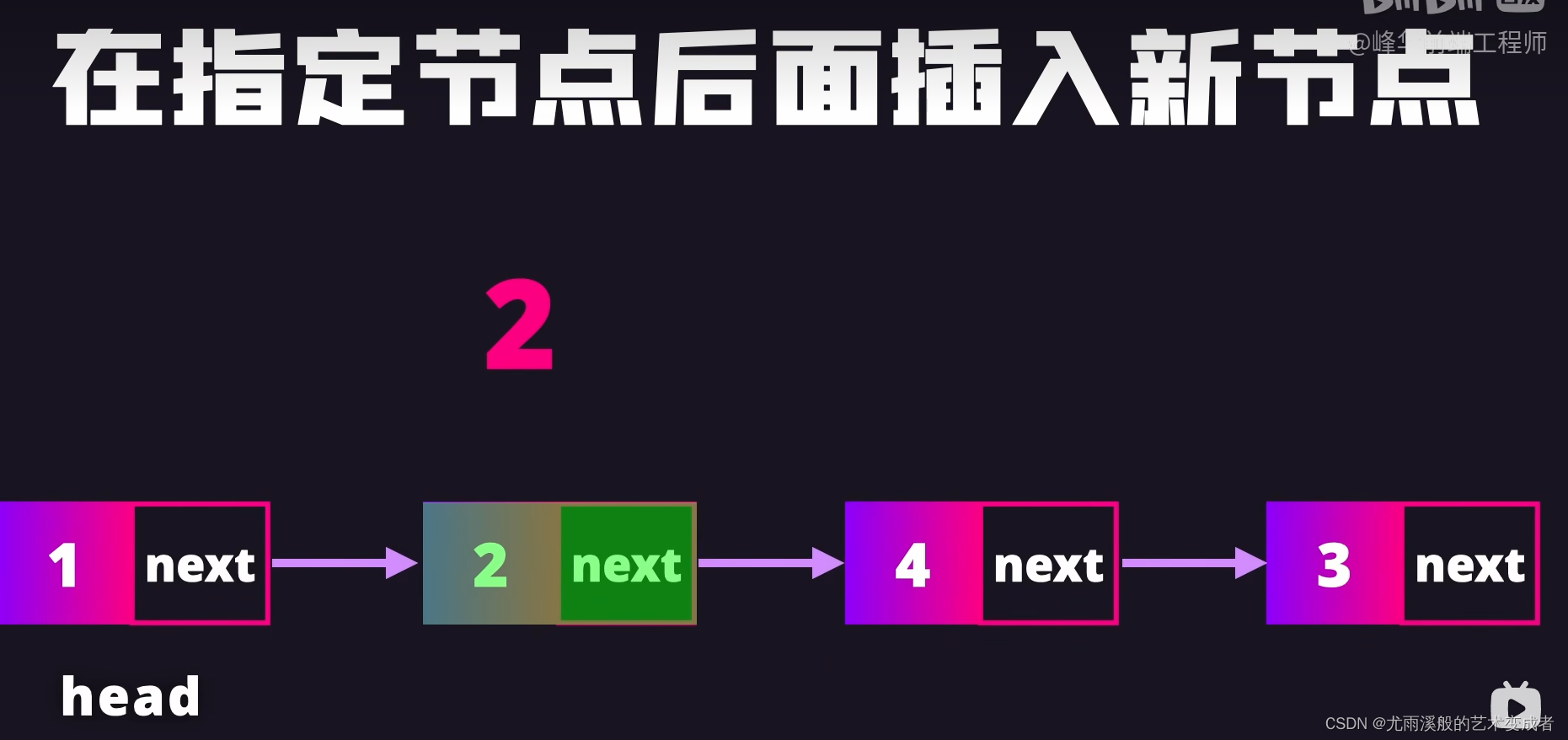
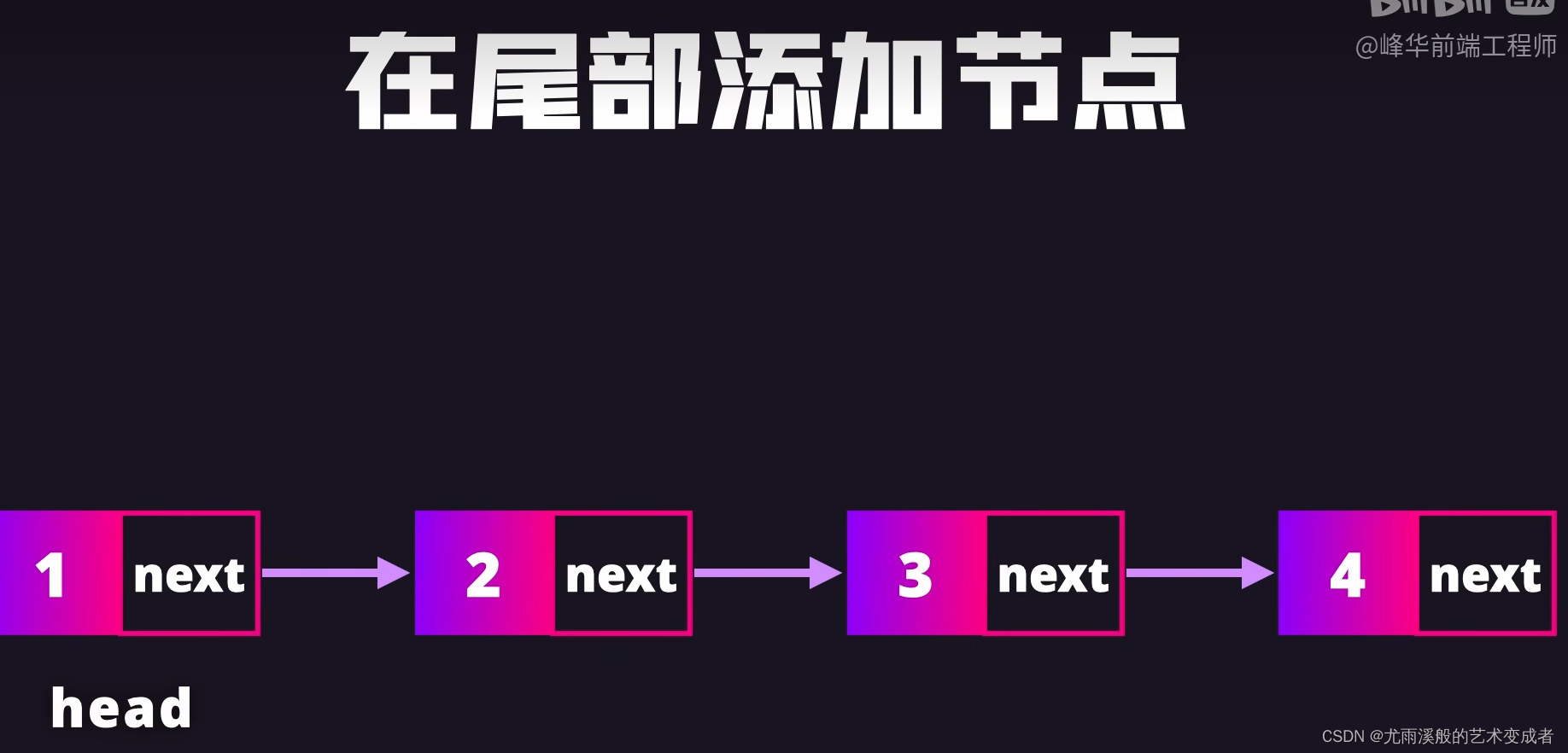
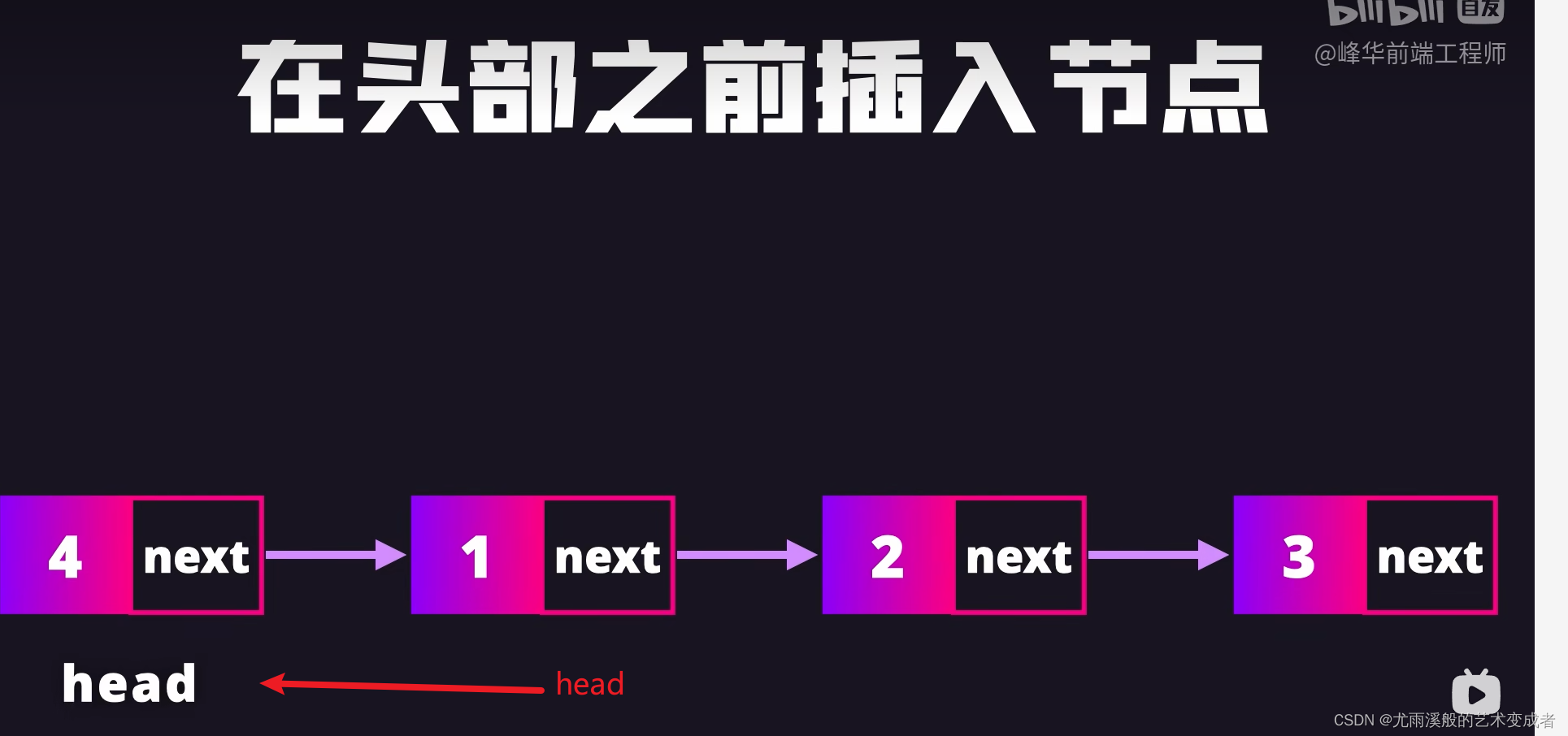
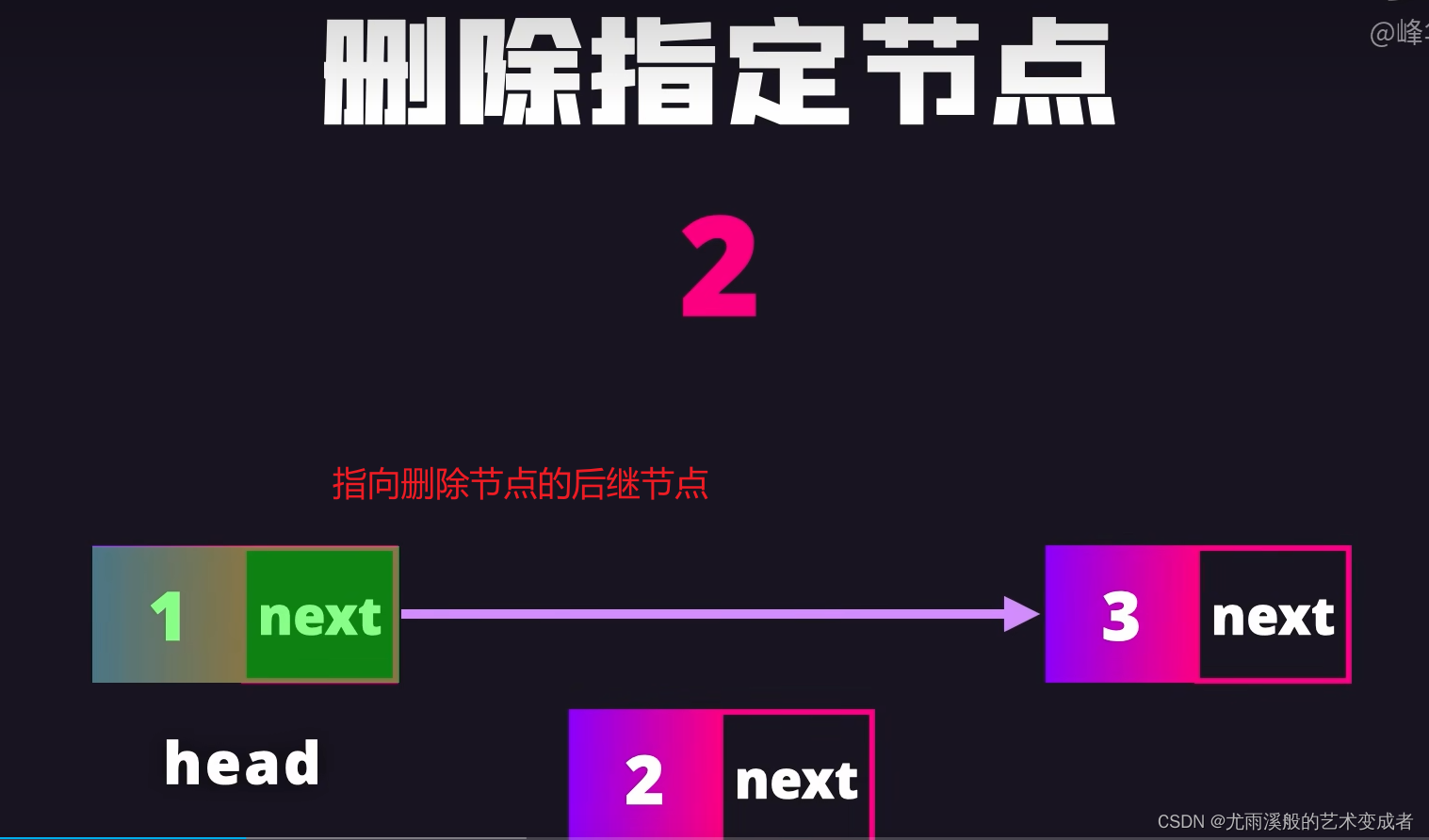
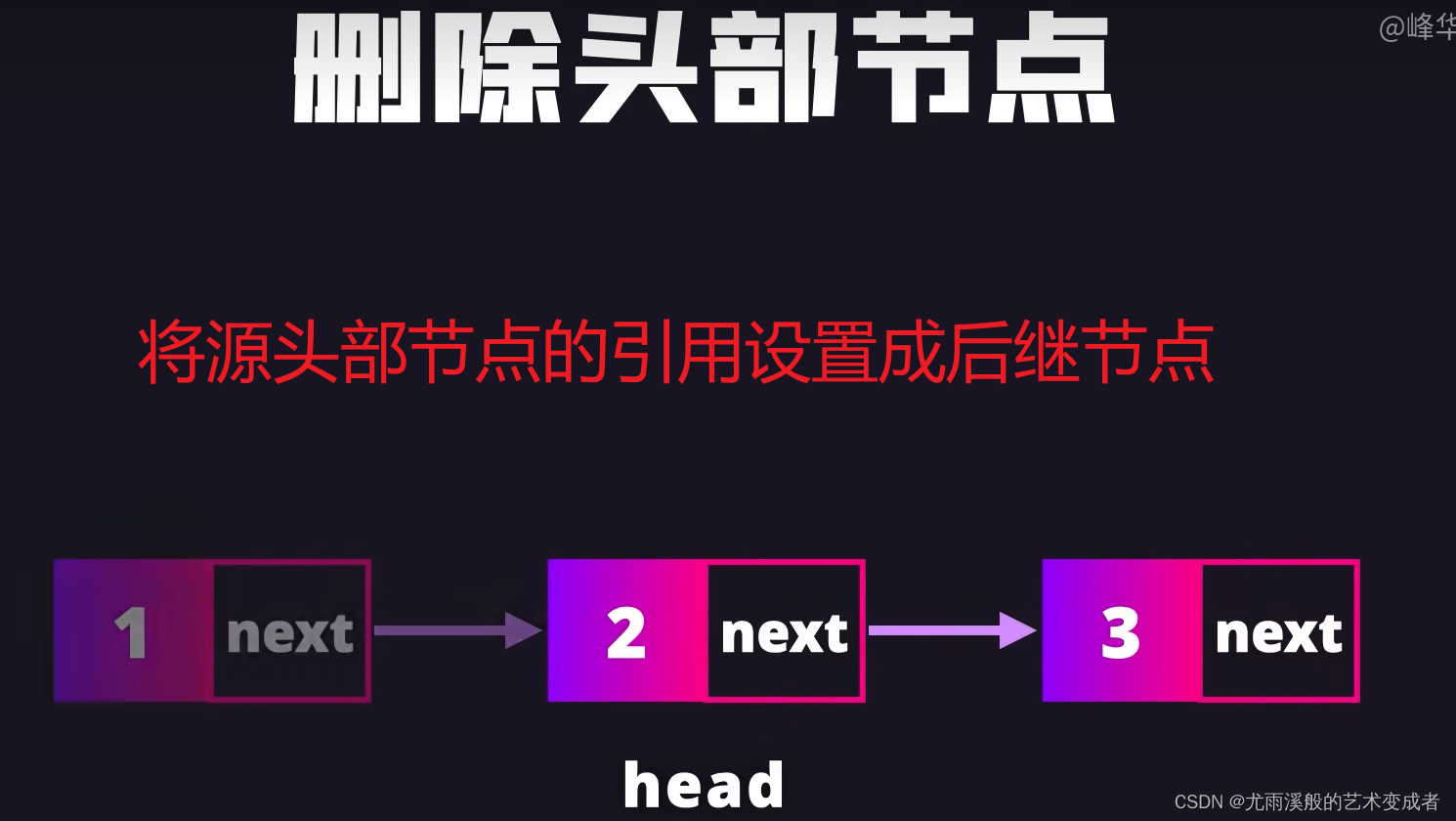

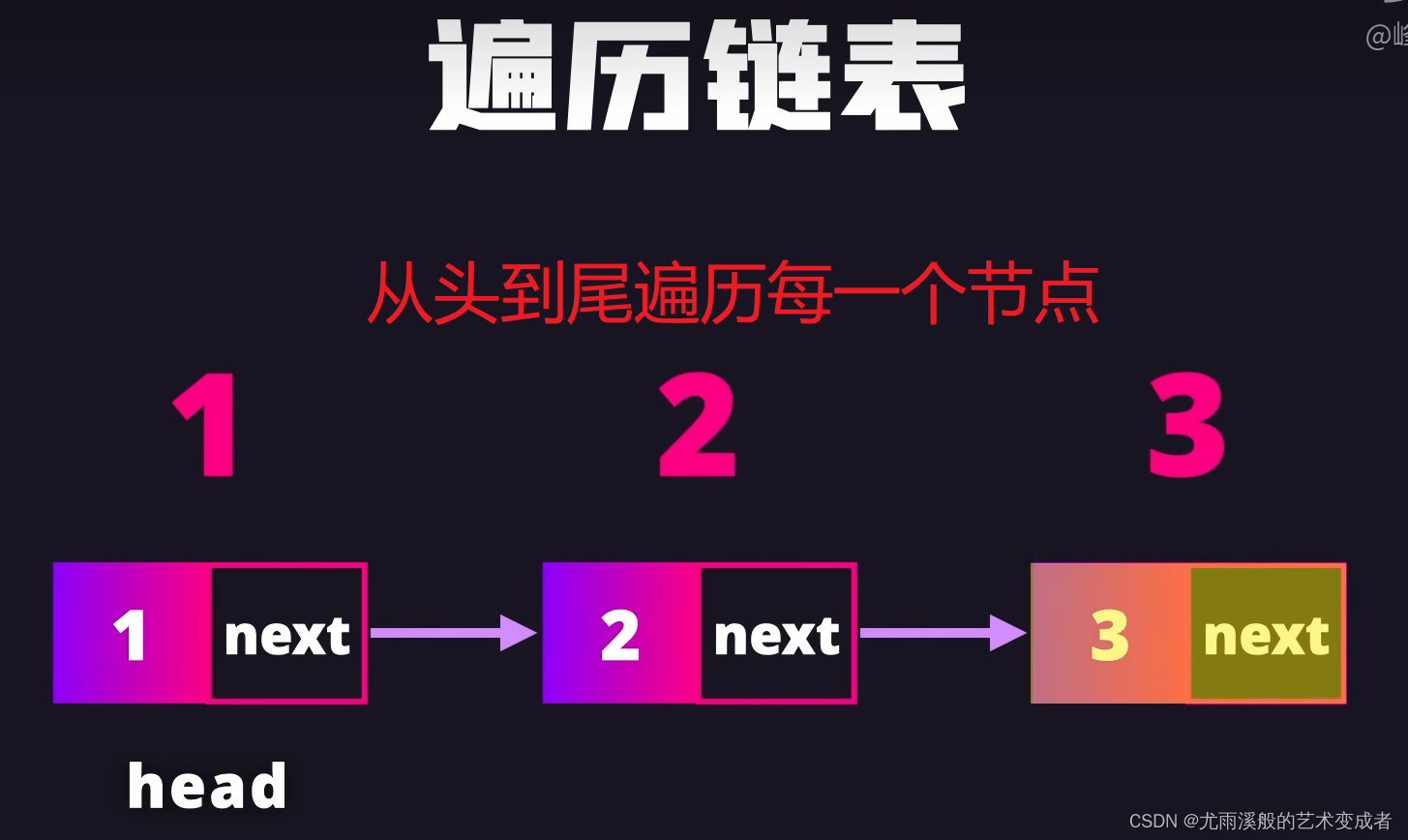



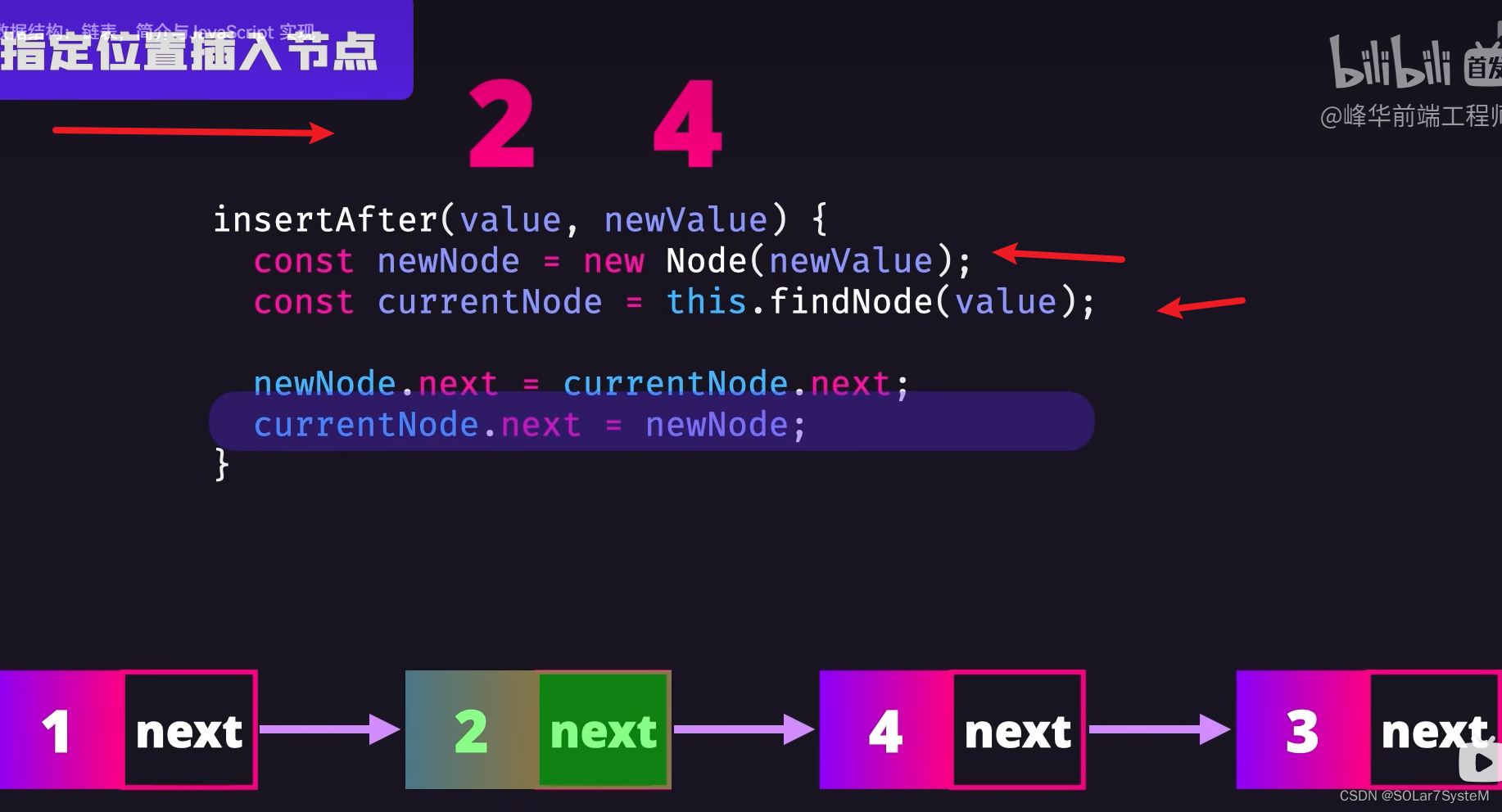
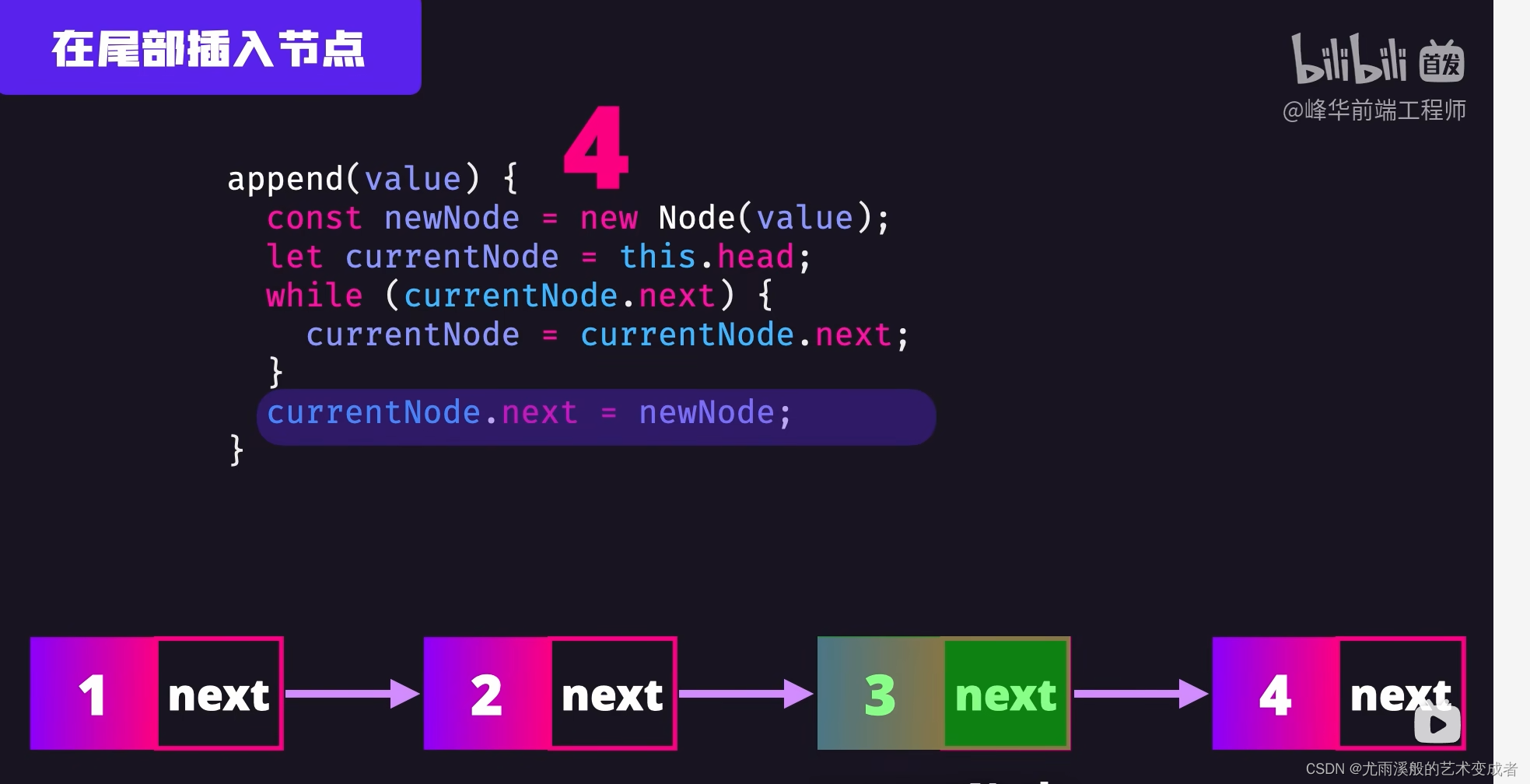
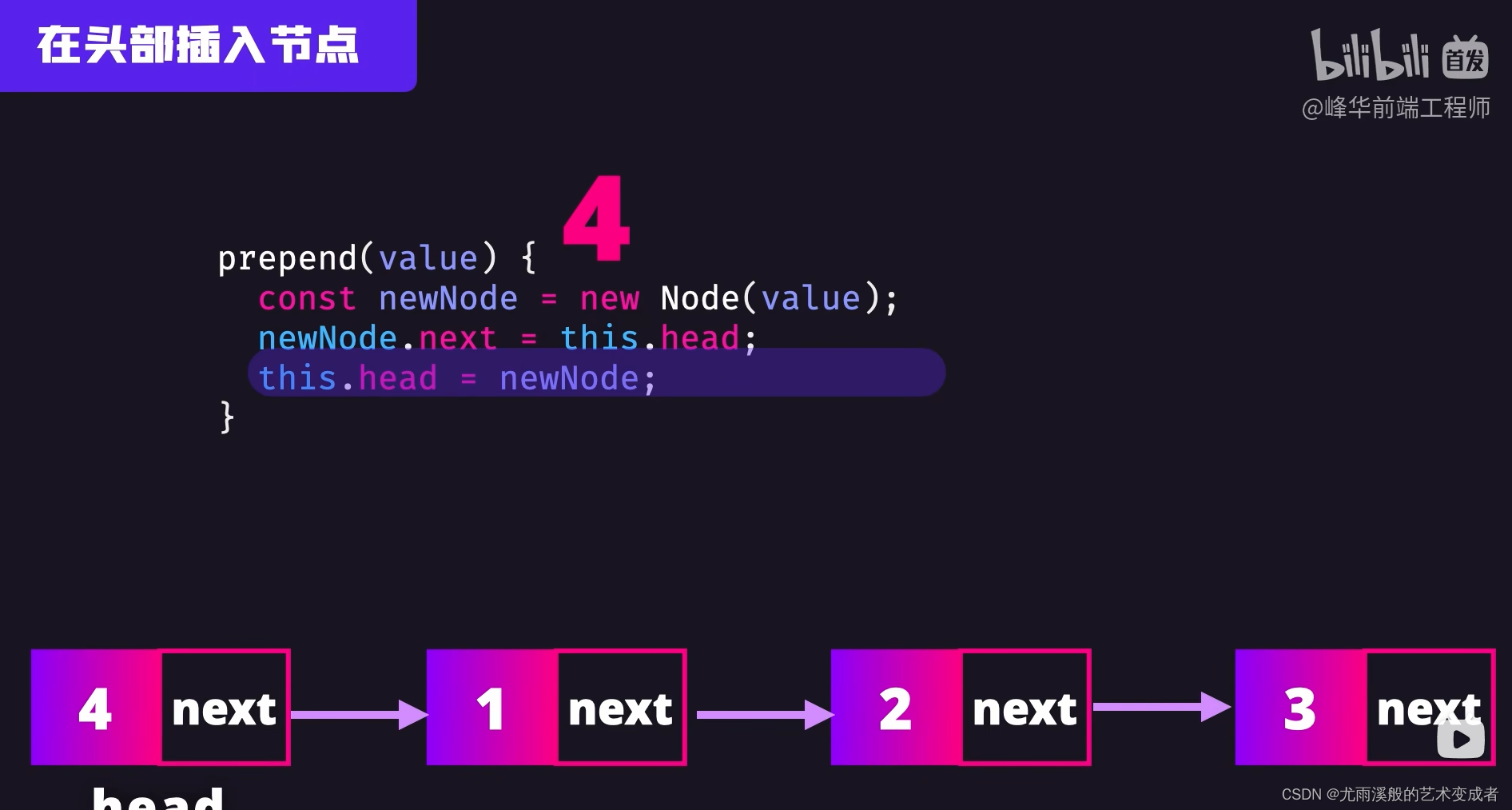
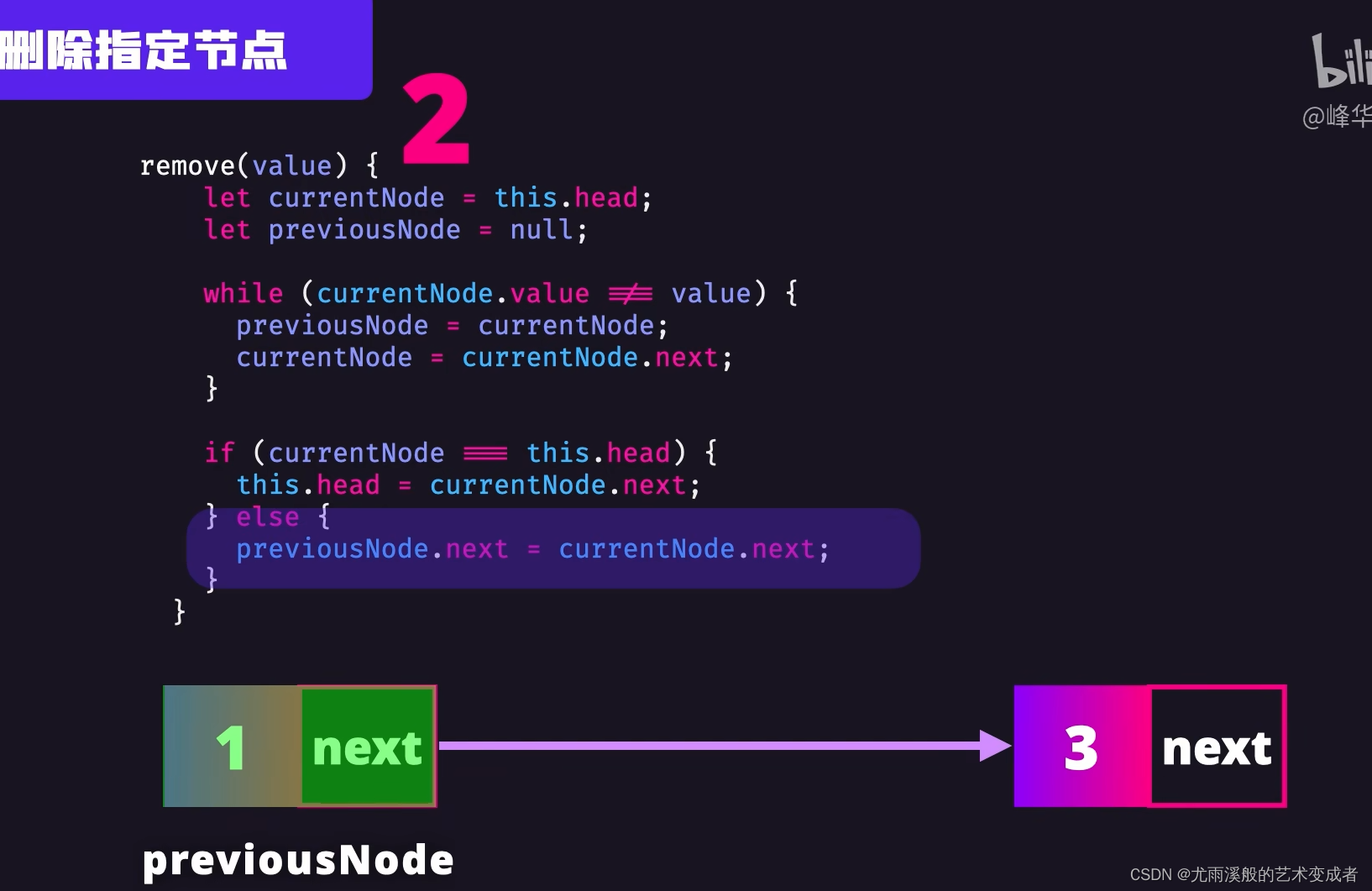


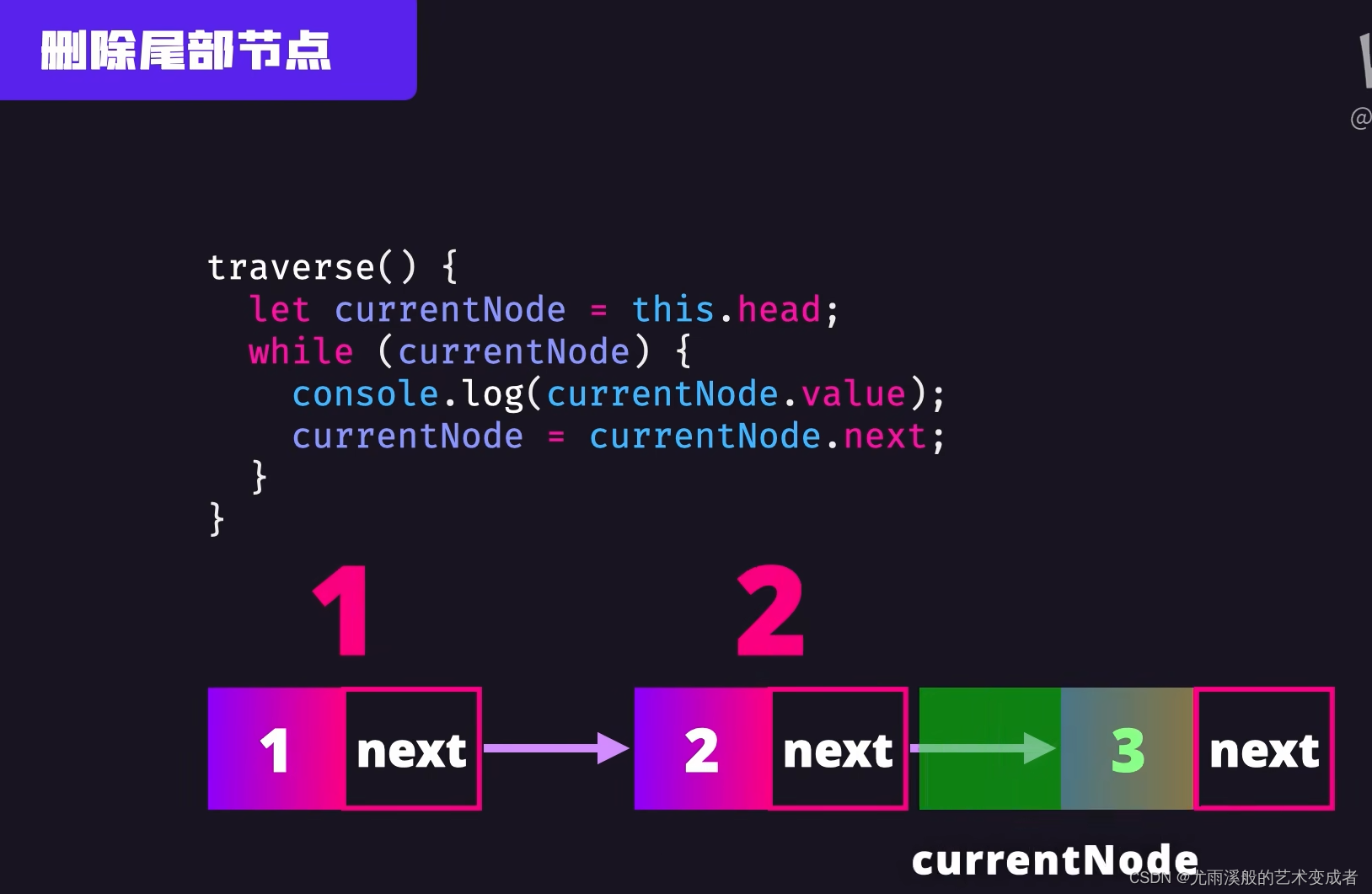
实例



队列











实例








栈


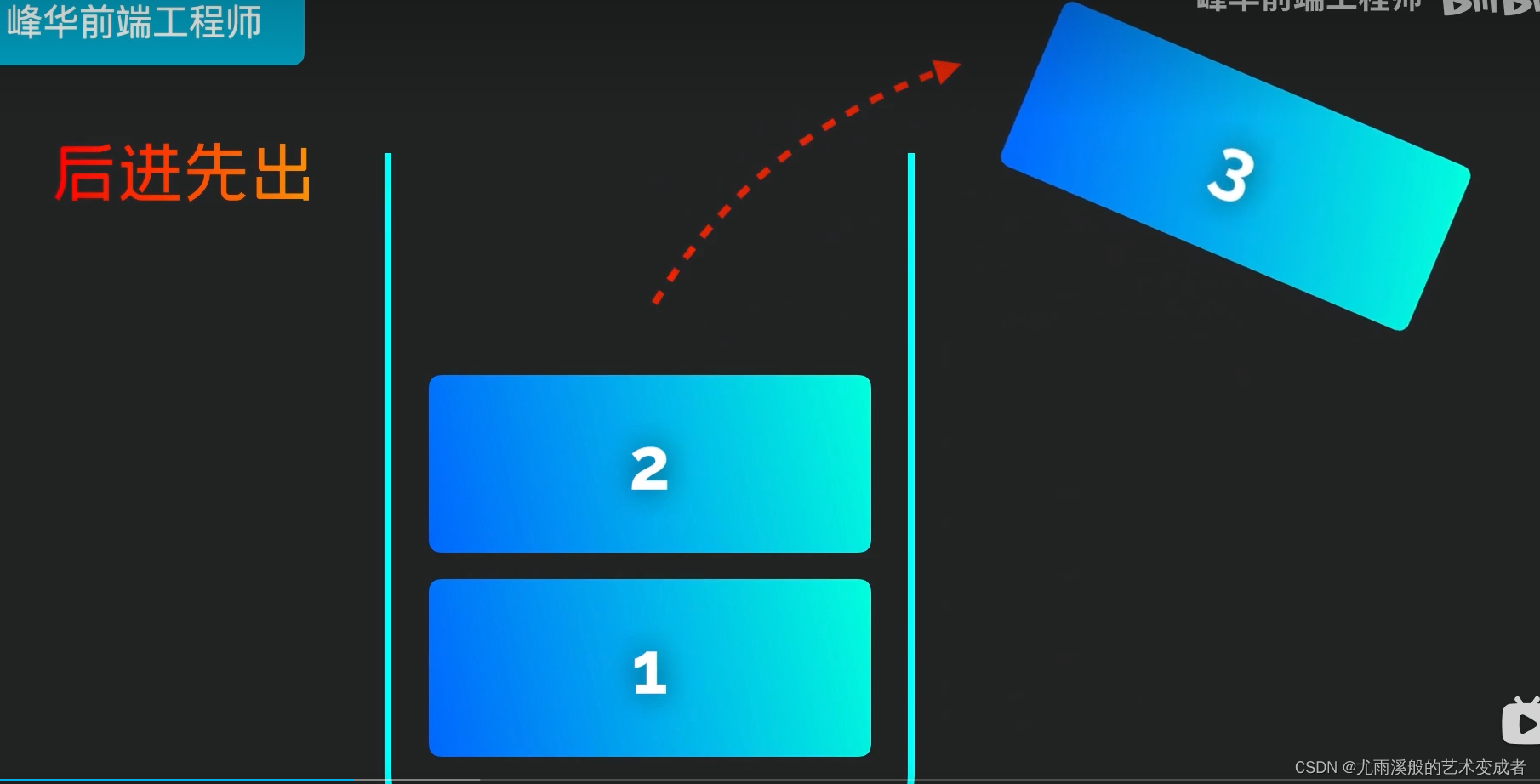

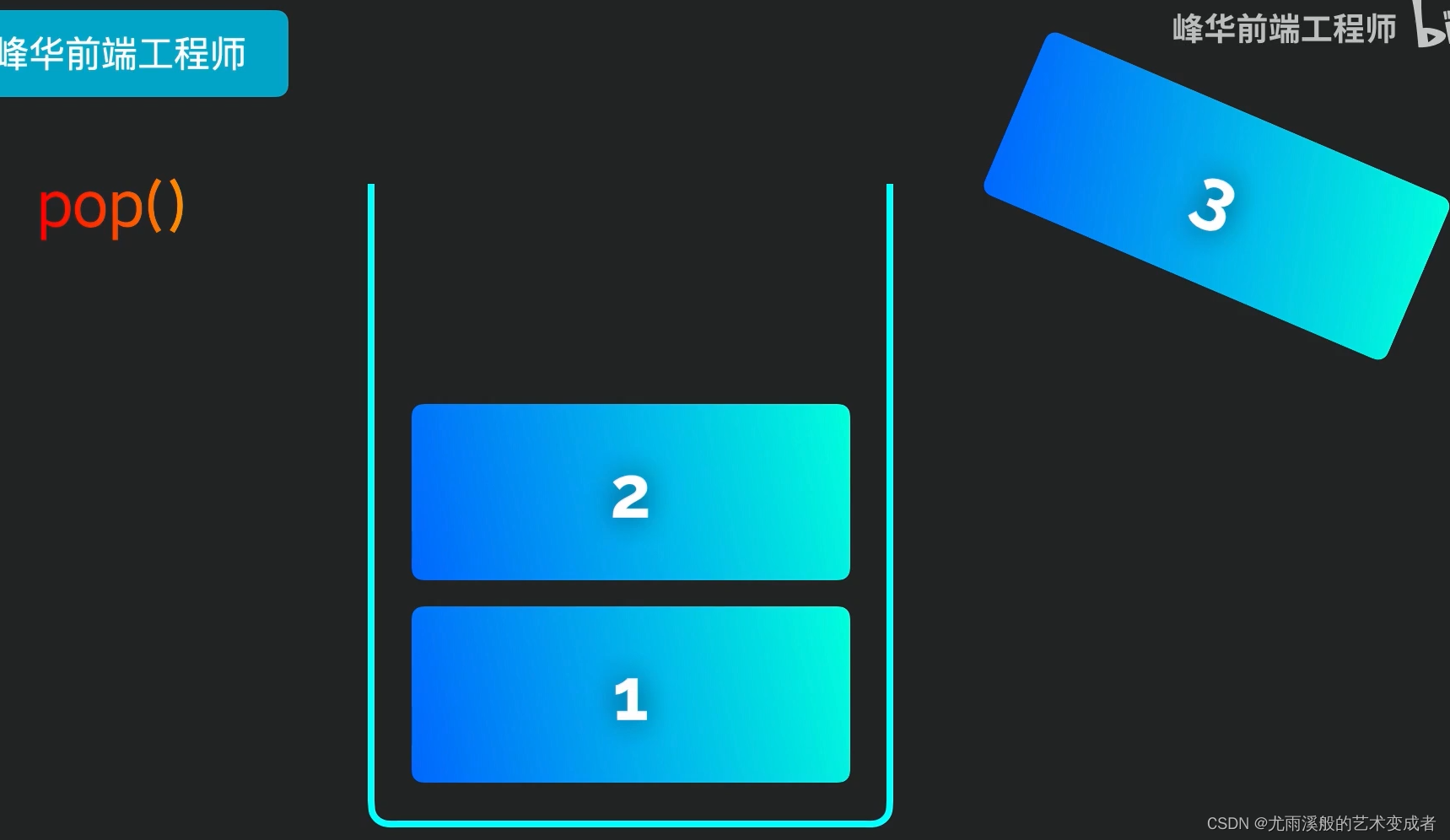
实例






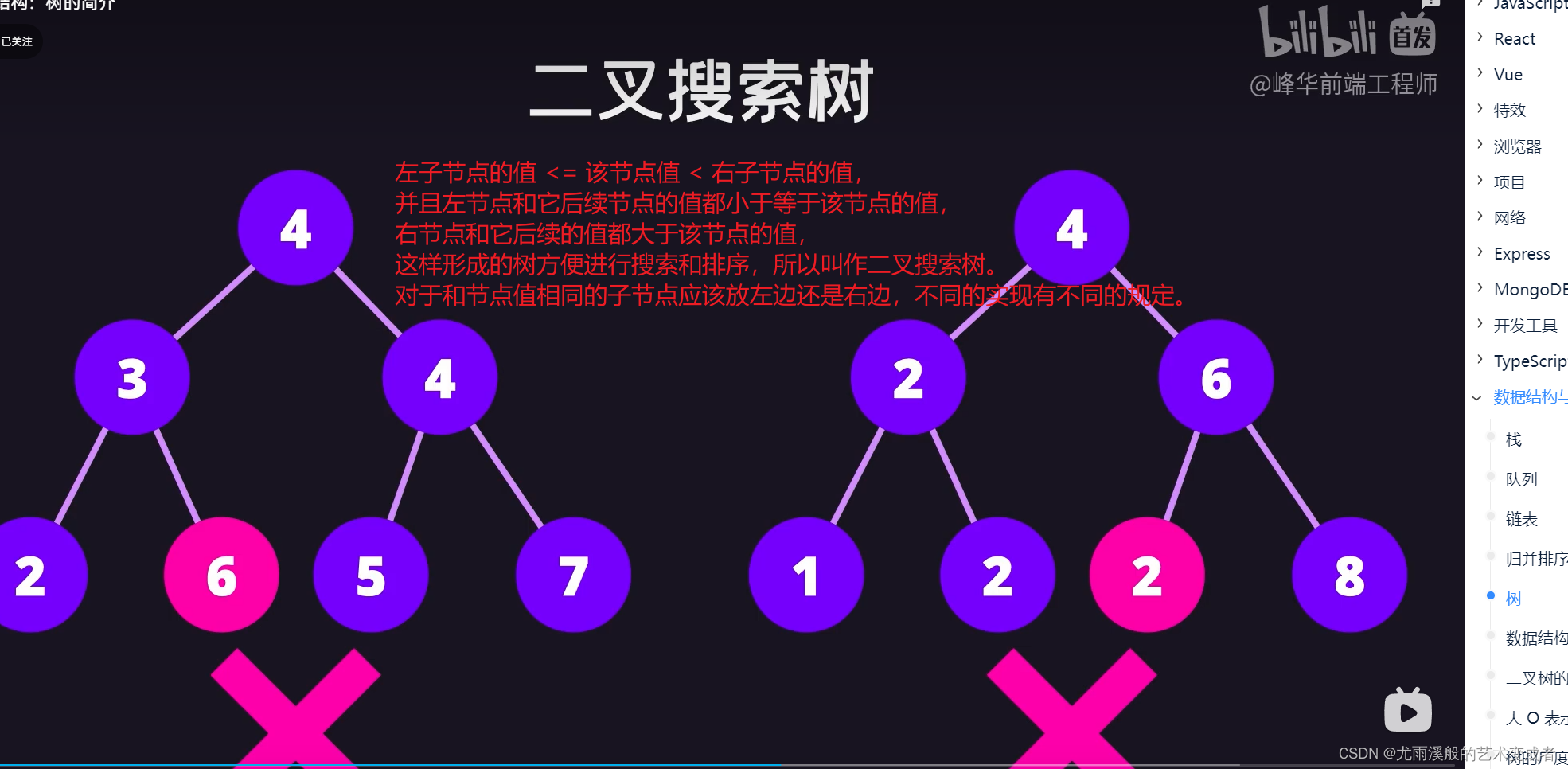
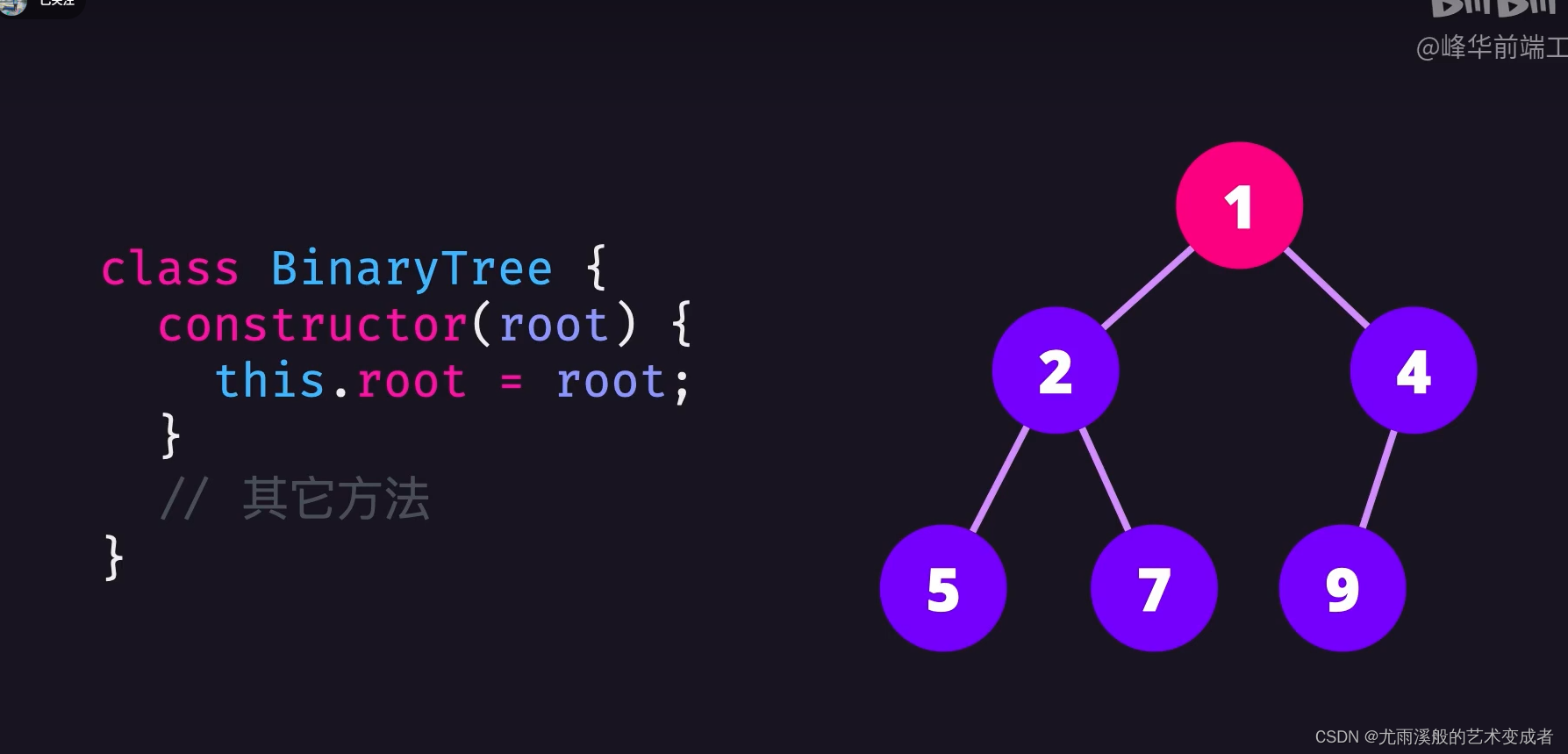
树
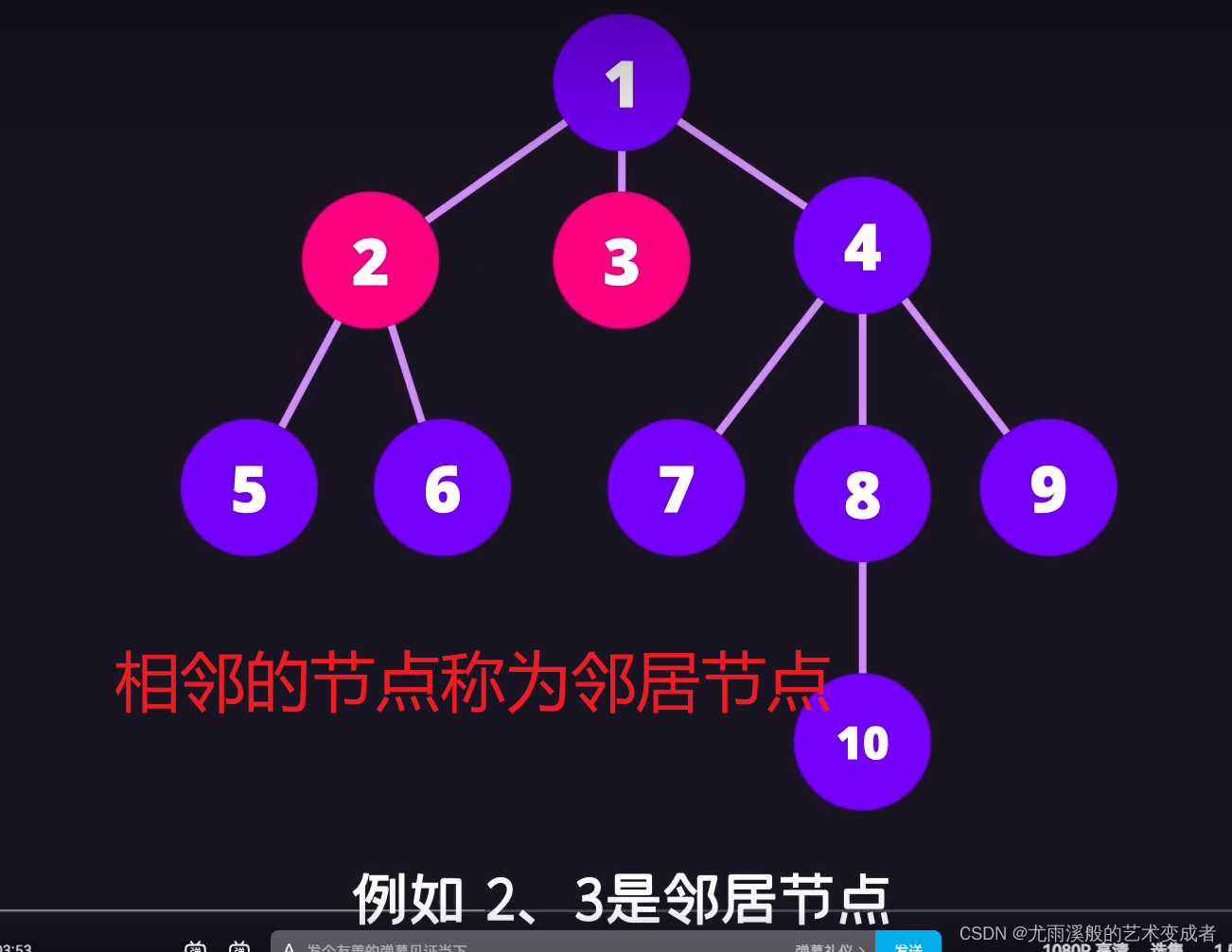
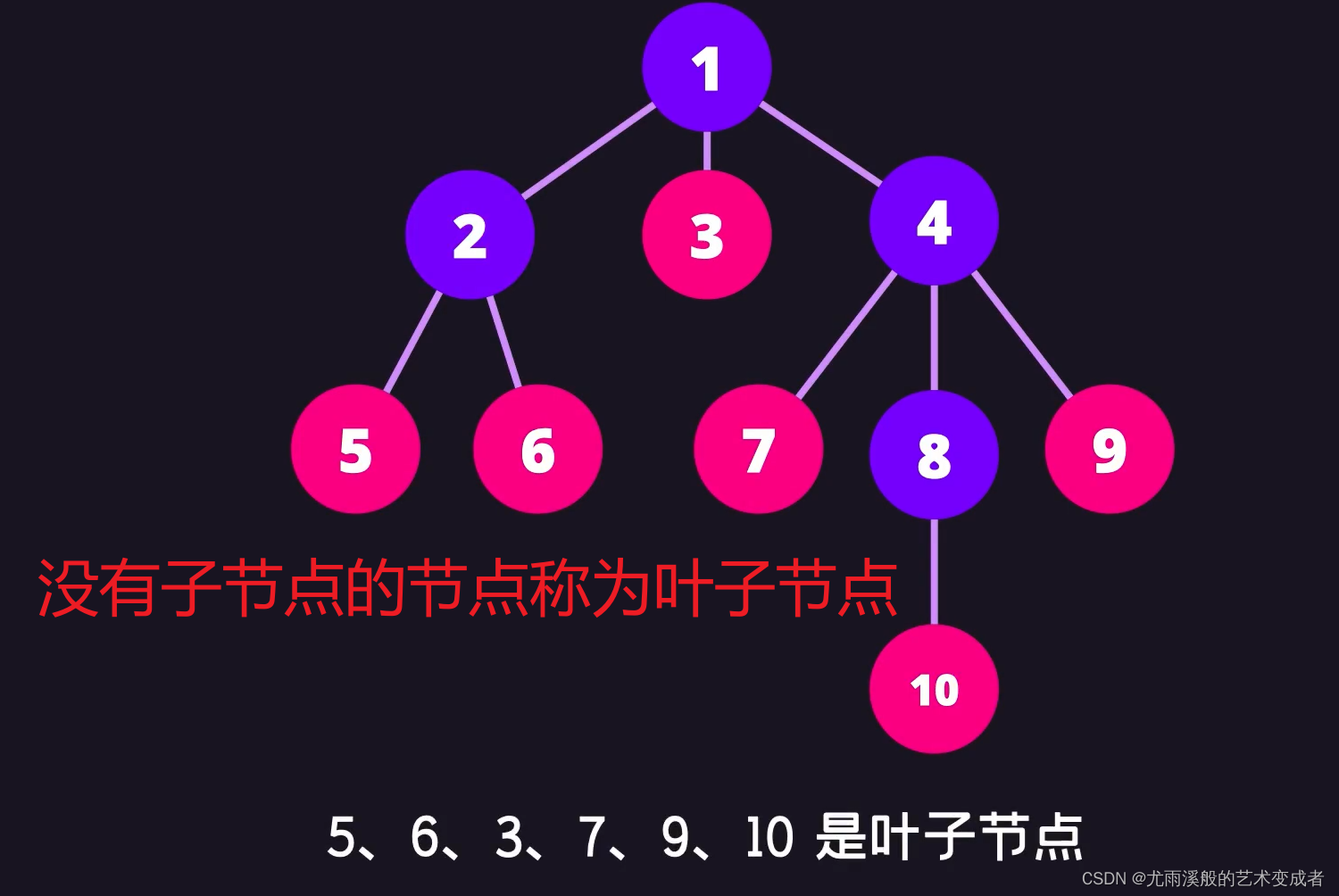

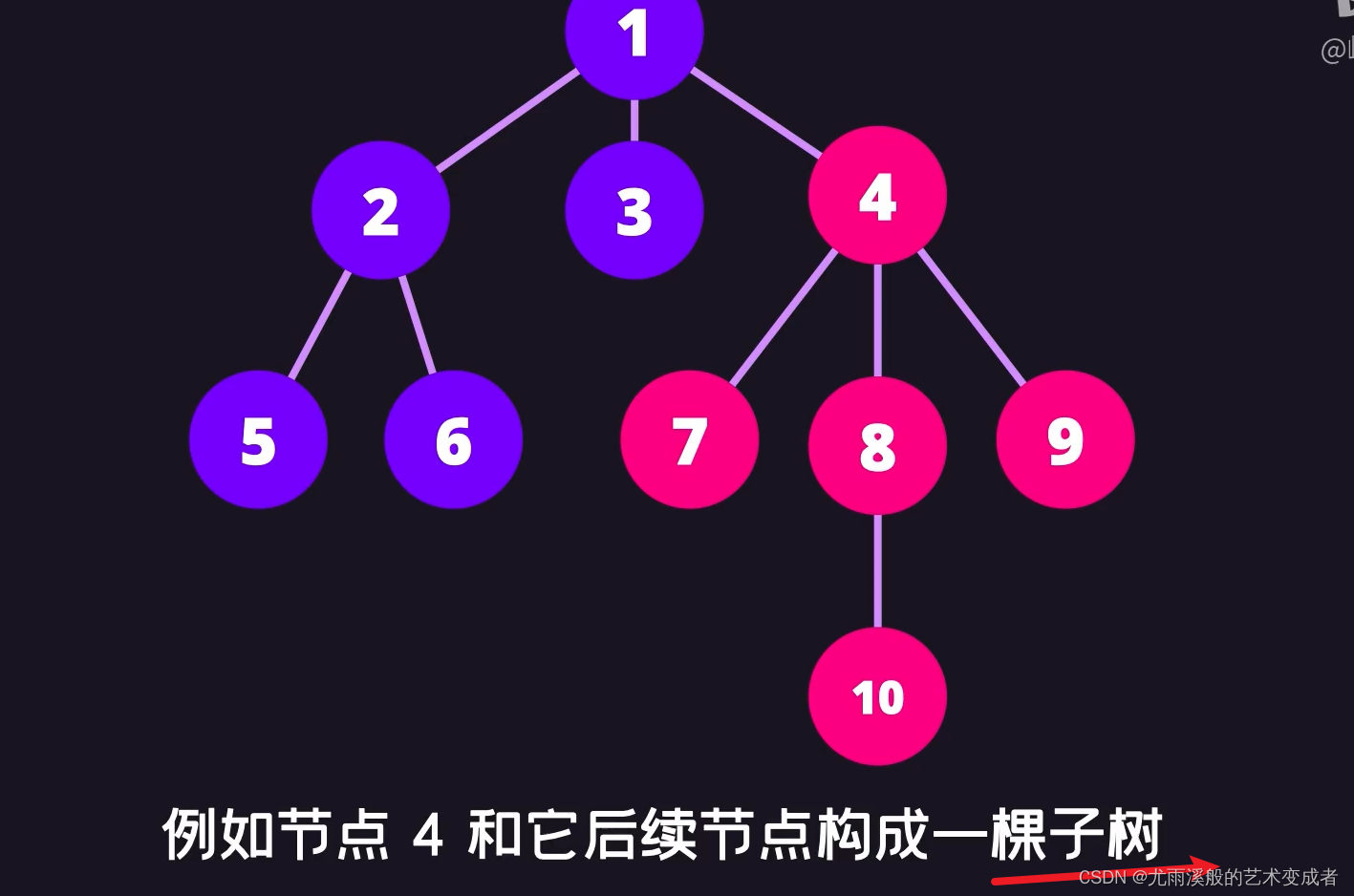

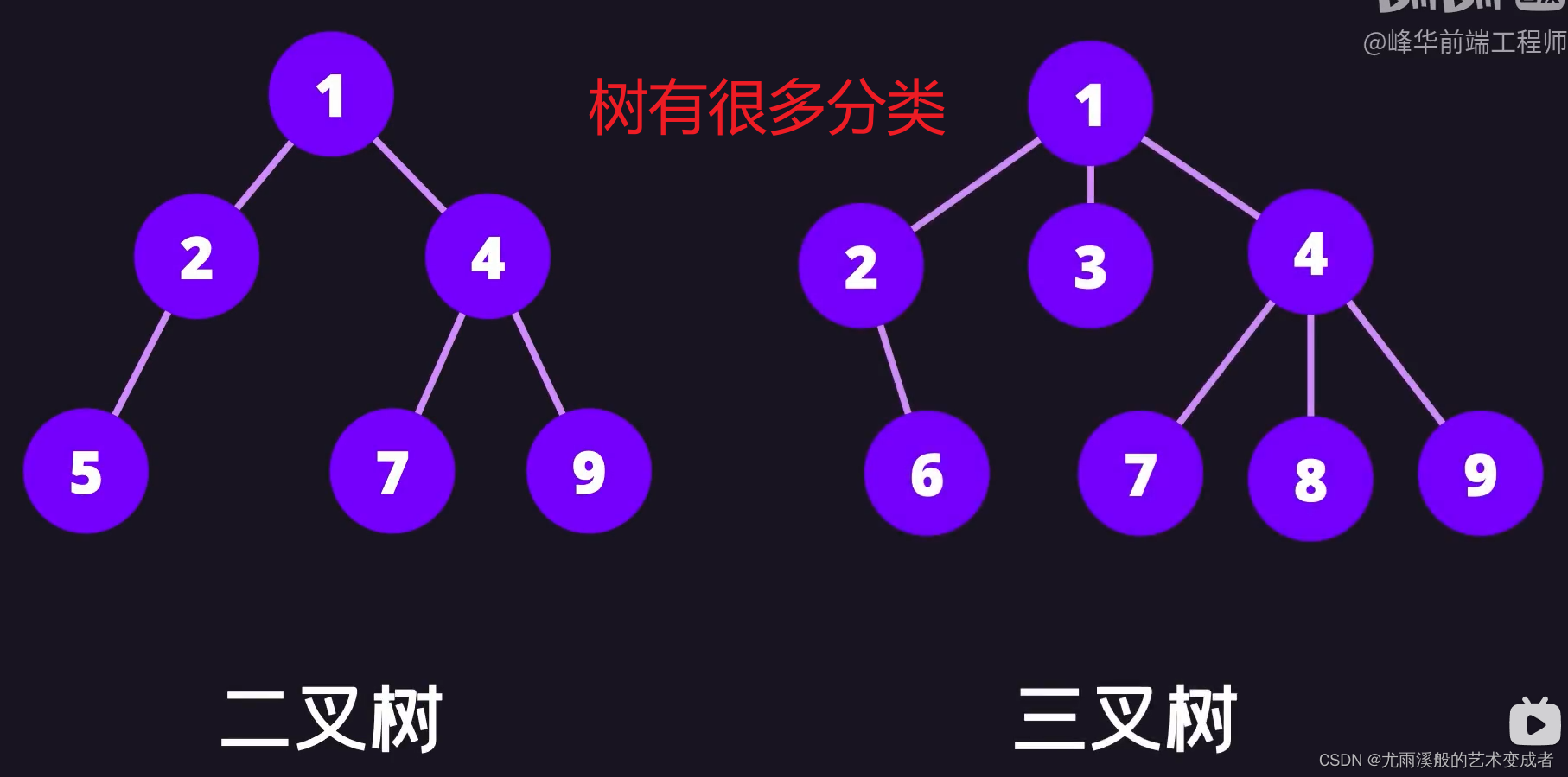
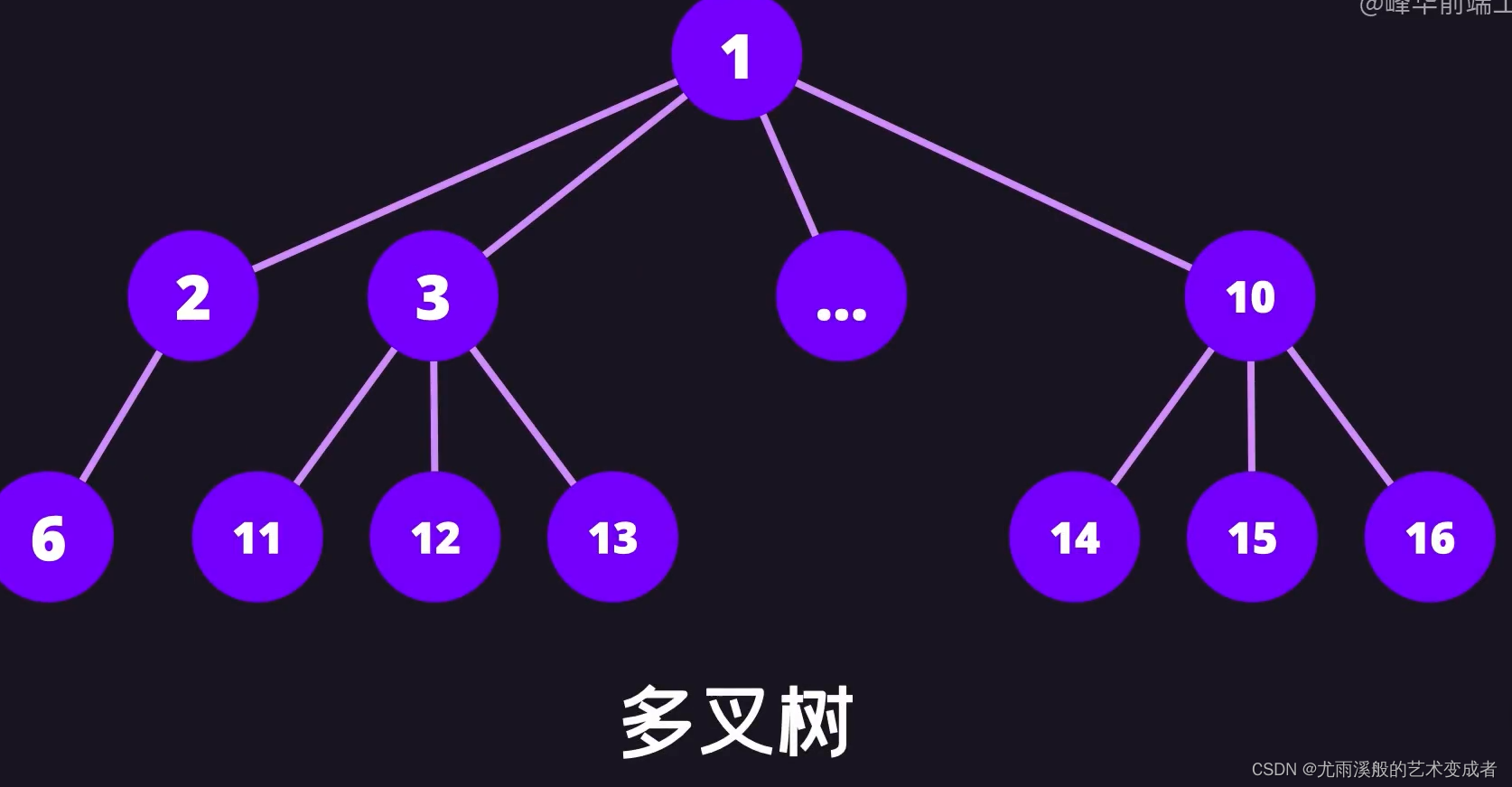
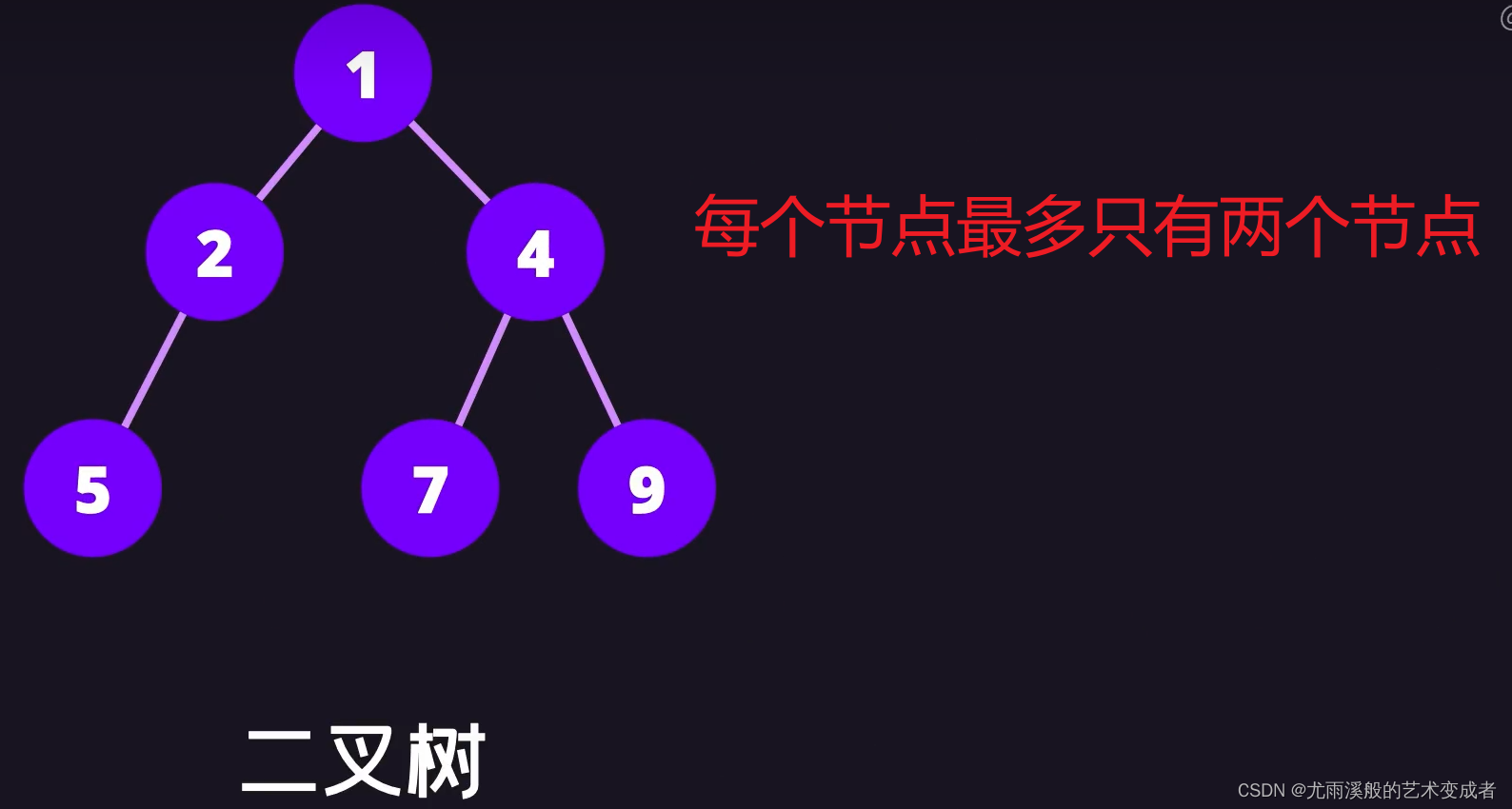
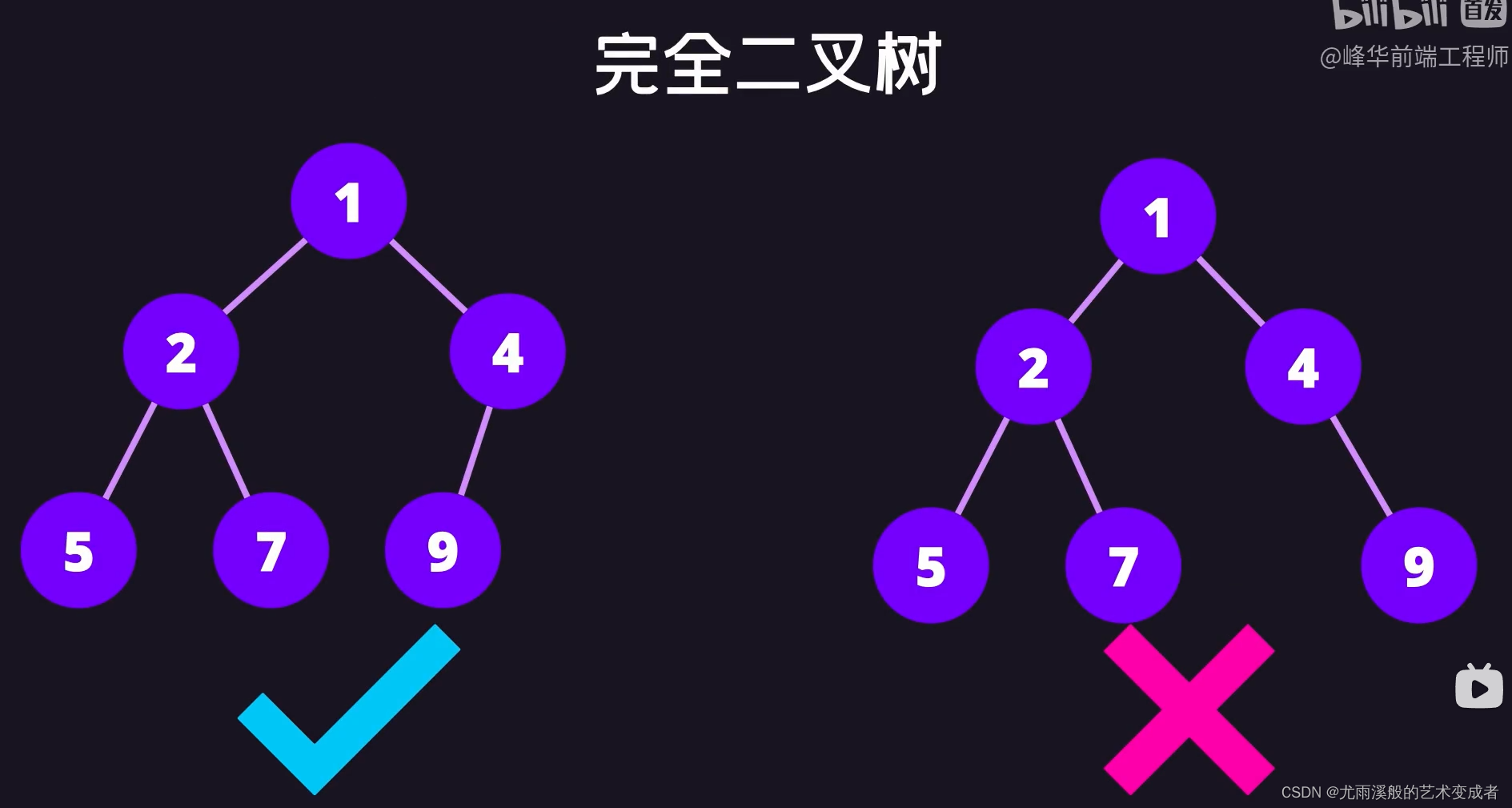
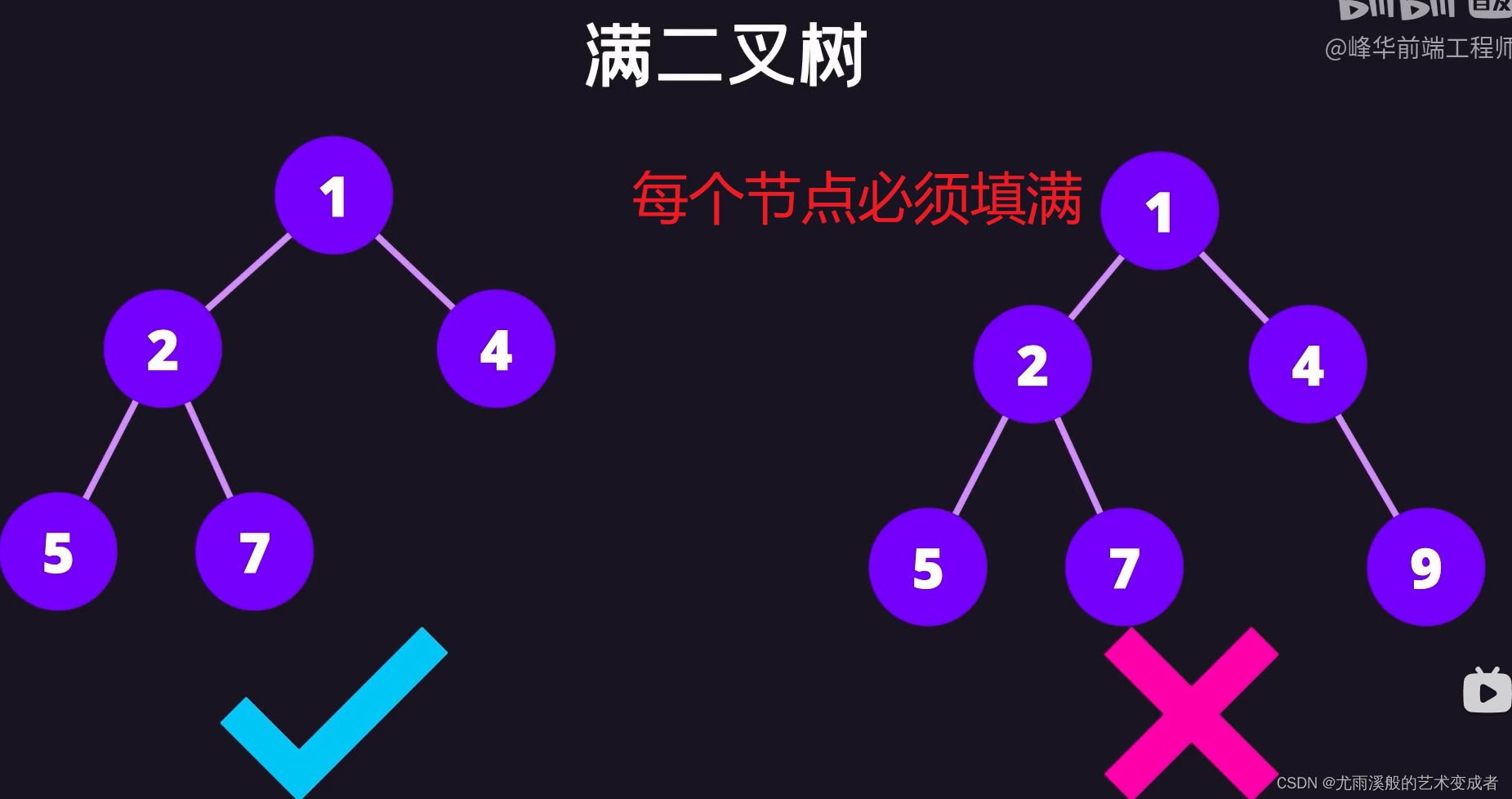
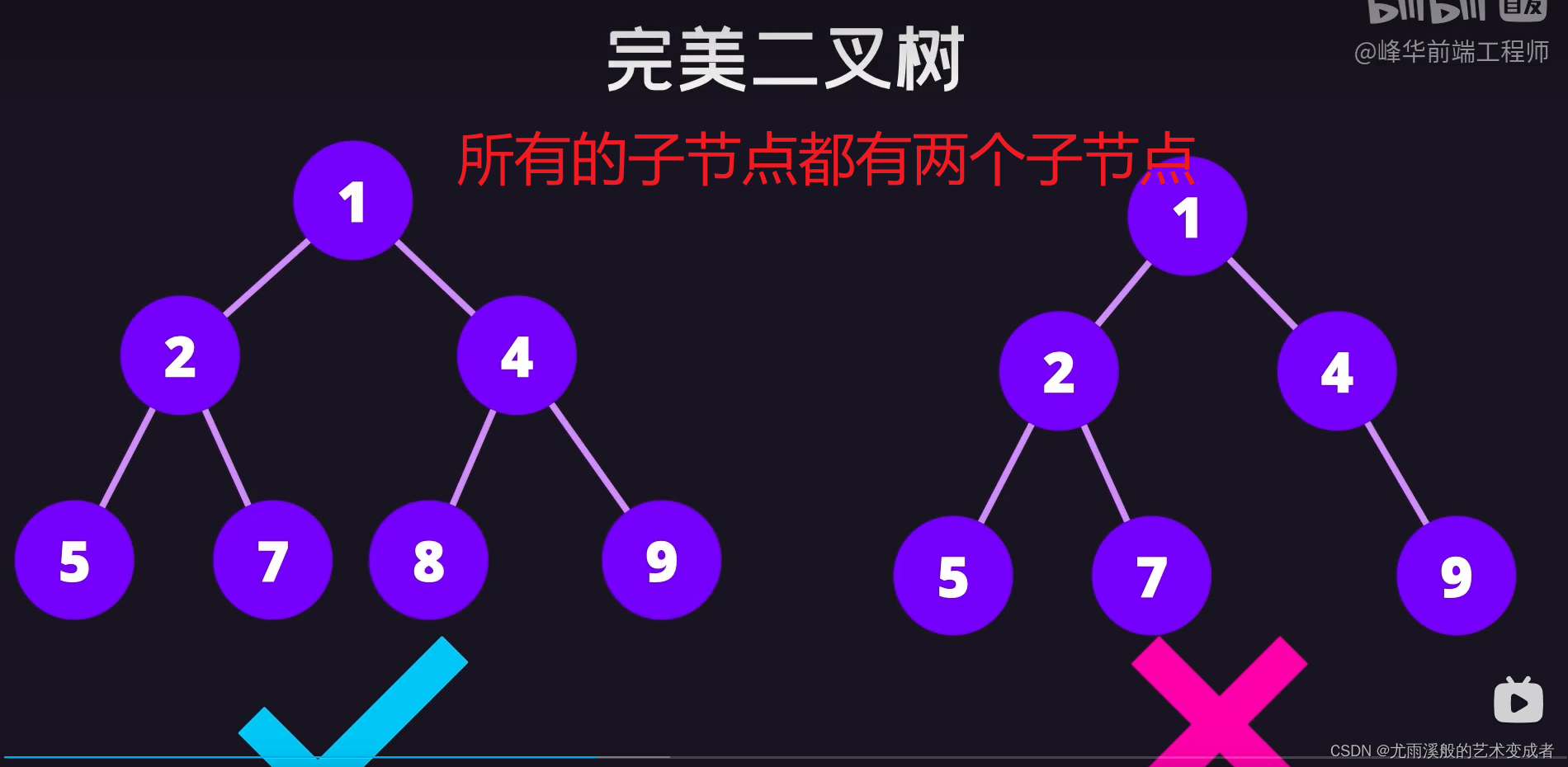
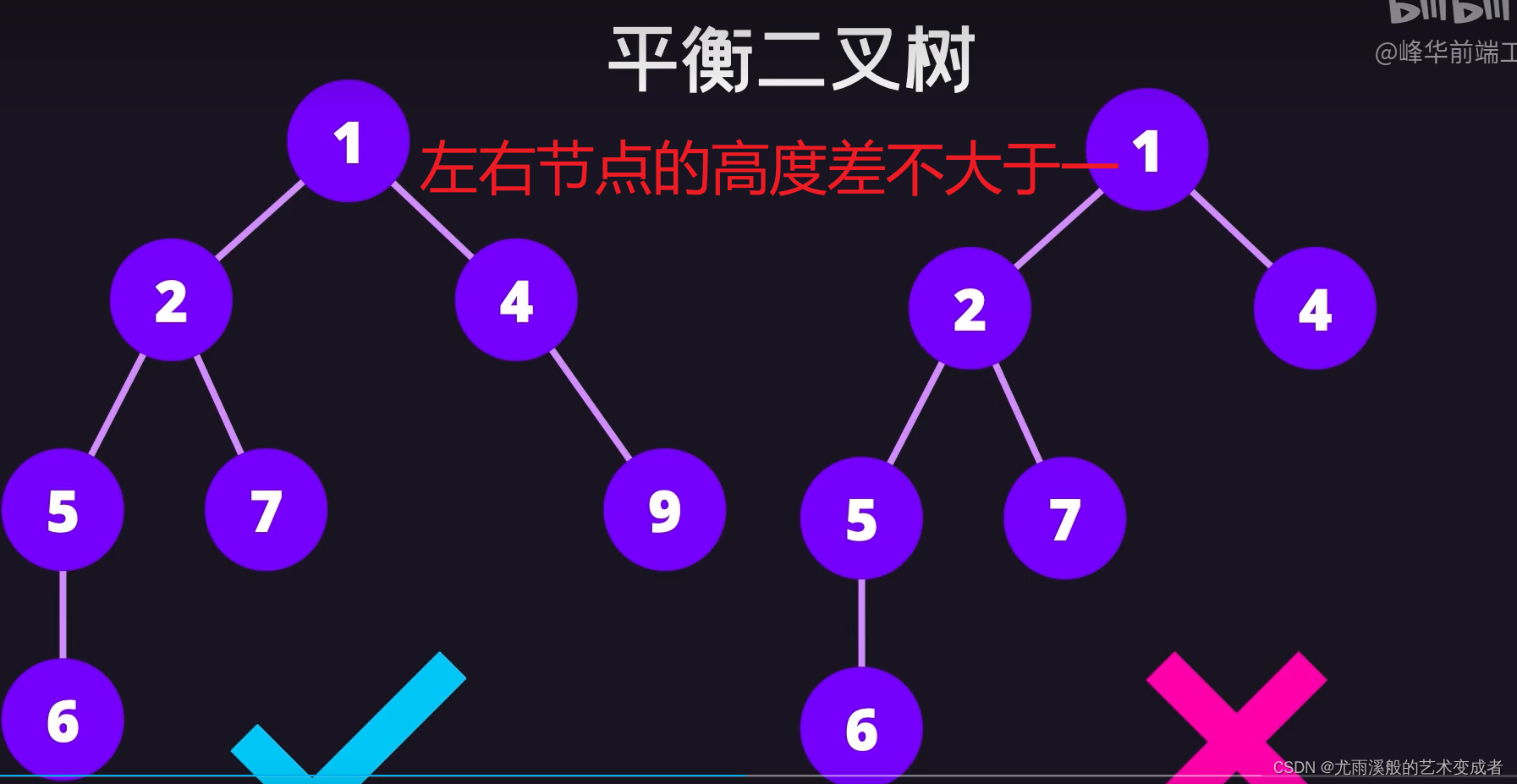
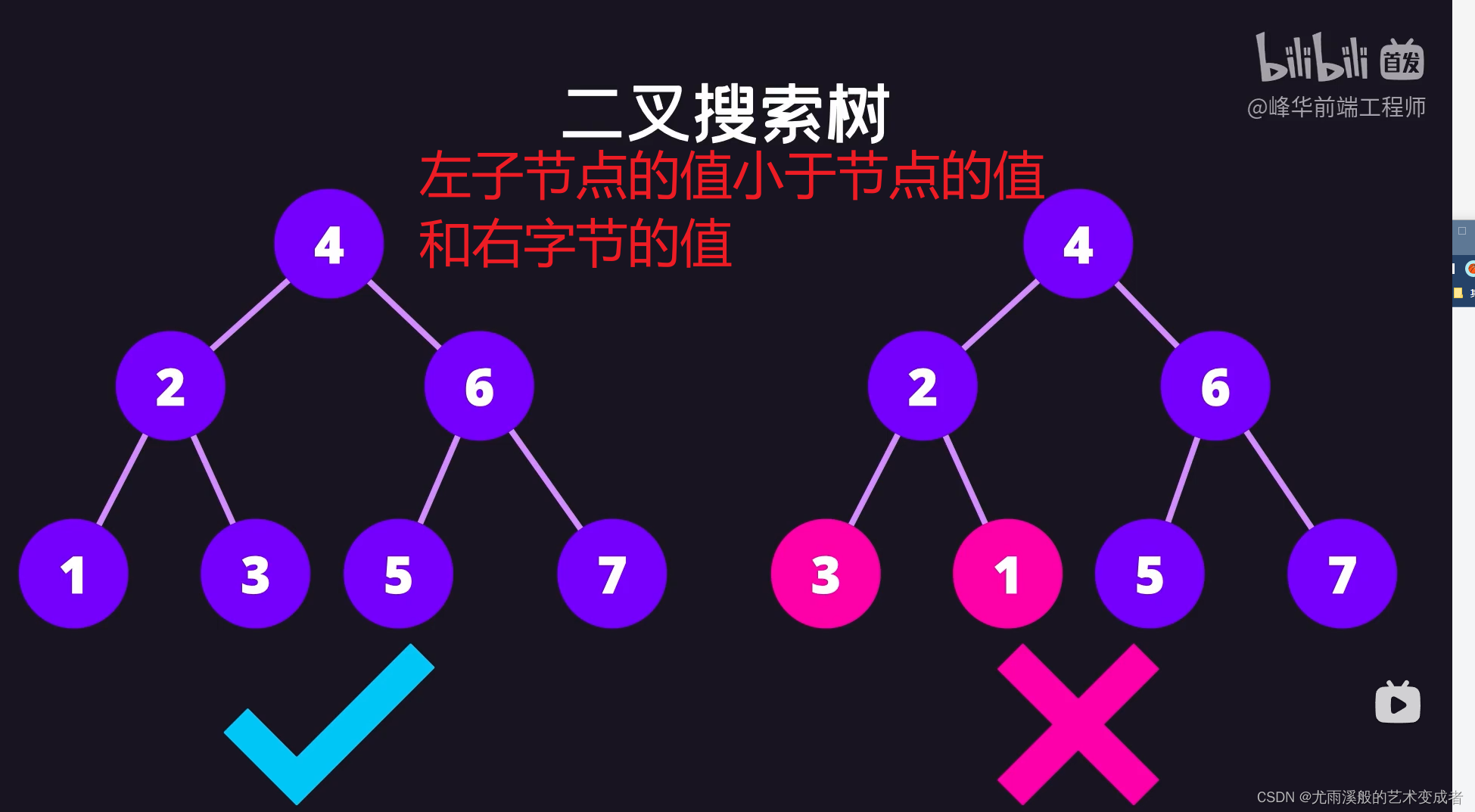
并且左节点的值和后续节点的值都要小于等于该节点的值

图
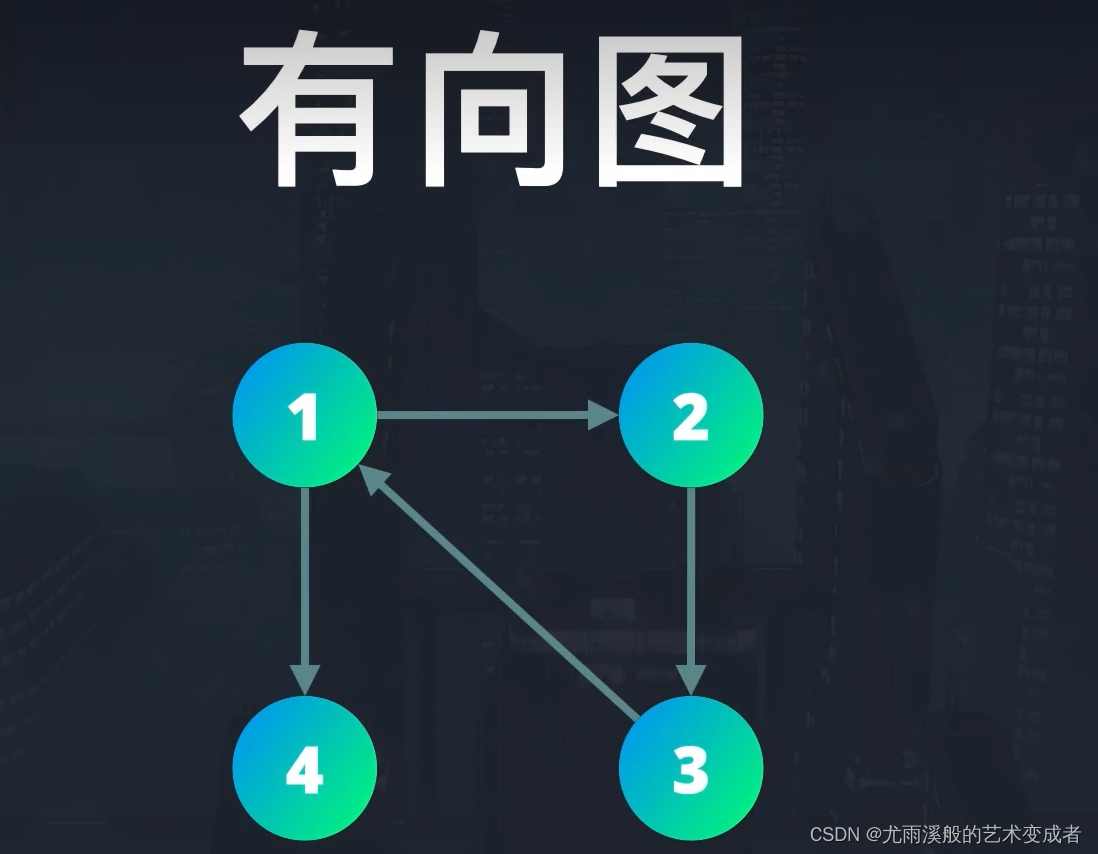
根据图的节点之间的边是否有方向,可以分为有向图和无向图。


在有向图中,访问节点只能按照指定的方向进行。
在无向图中,可以以任意方向访问节点,因此它也容易构成环。
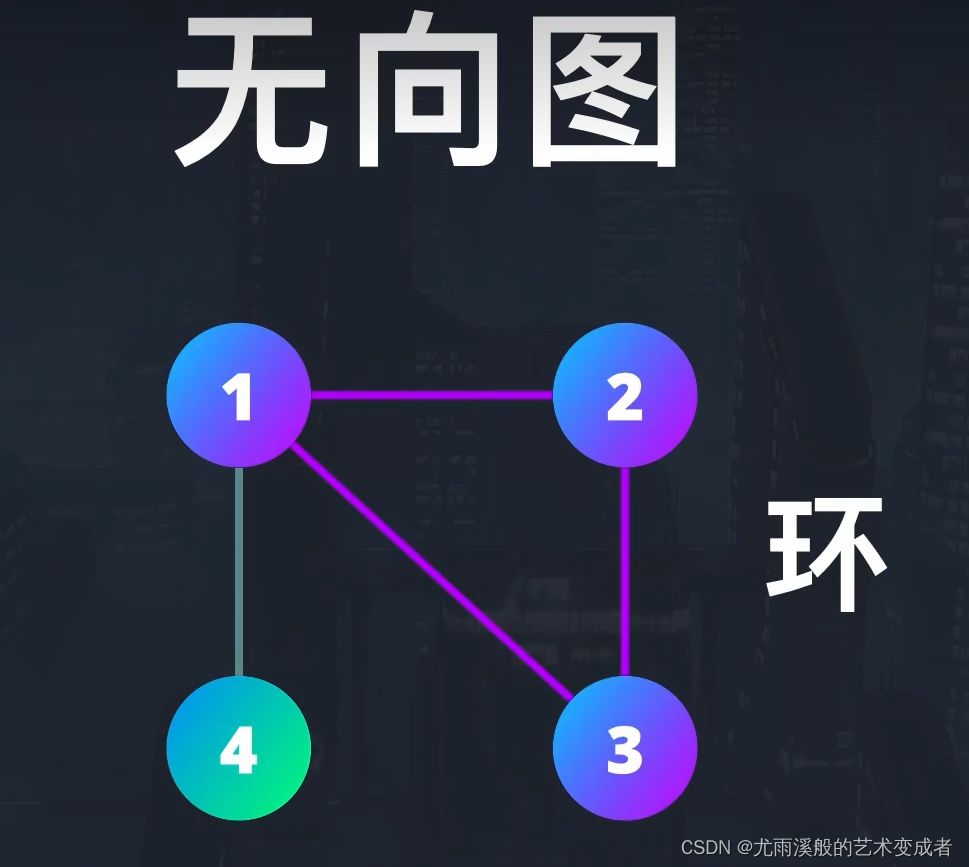
根据图的节点是否都可以遍历到,还分为连通图和非连通图(或叫作隔离图):

连通图中的每个节点都有连接的边。
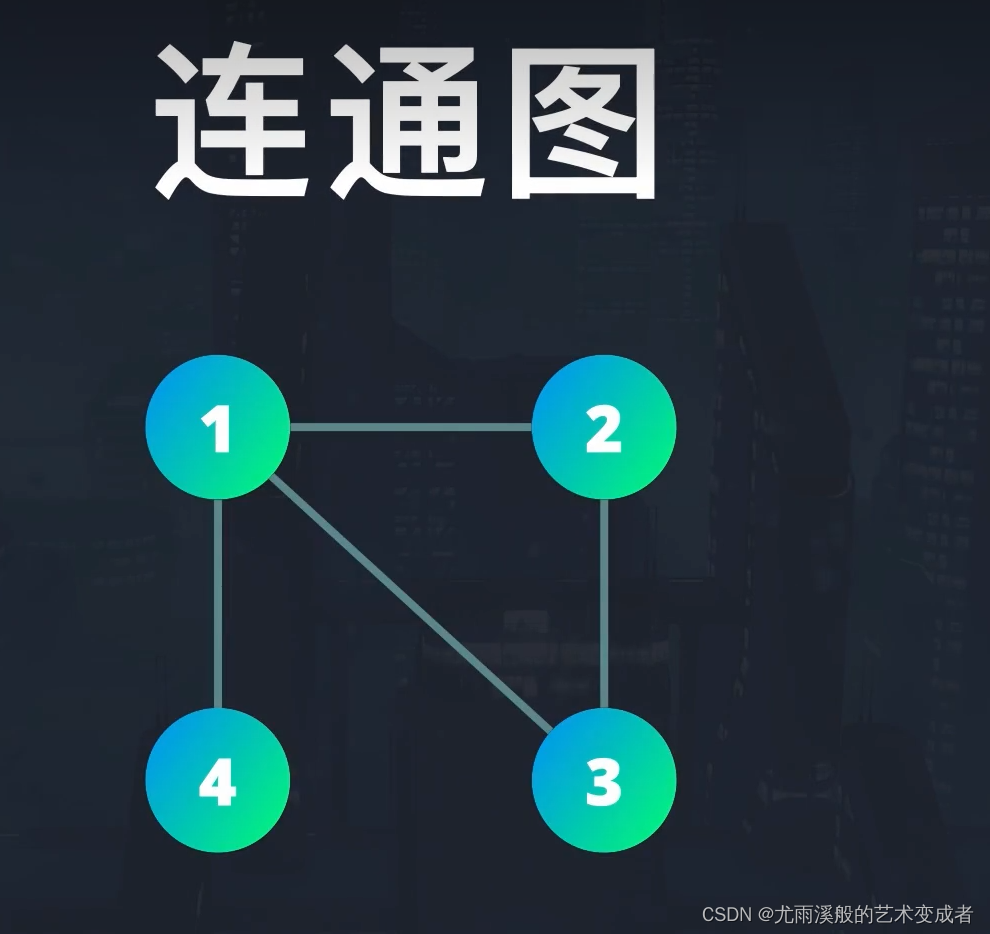
非连通图则是由多个独立的图构成,它们之间没有边连接。

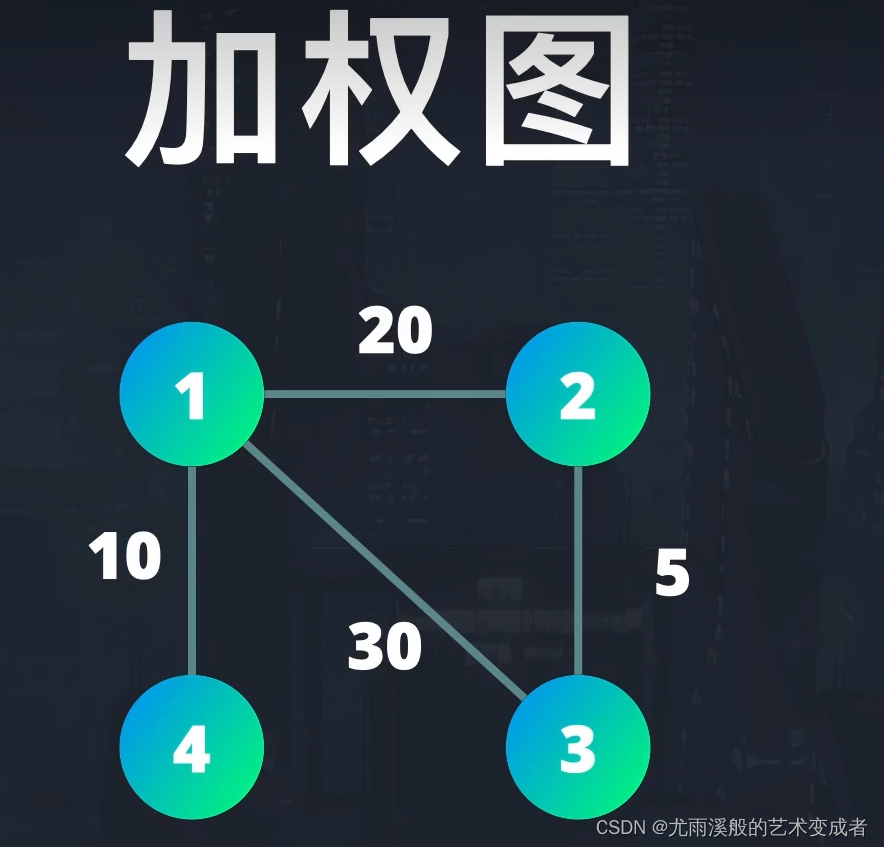
另外,如果连接节点的边还包含有额外信息,例如长度,那么这种图称为加权图。
使用代码表示图有多种方式,常见的有:
使用邻接矩阵。
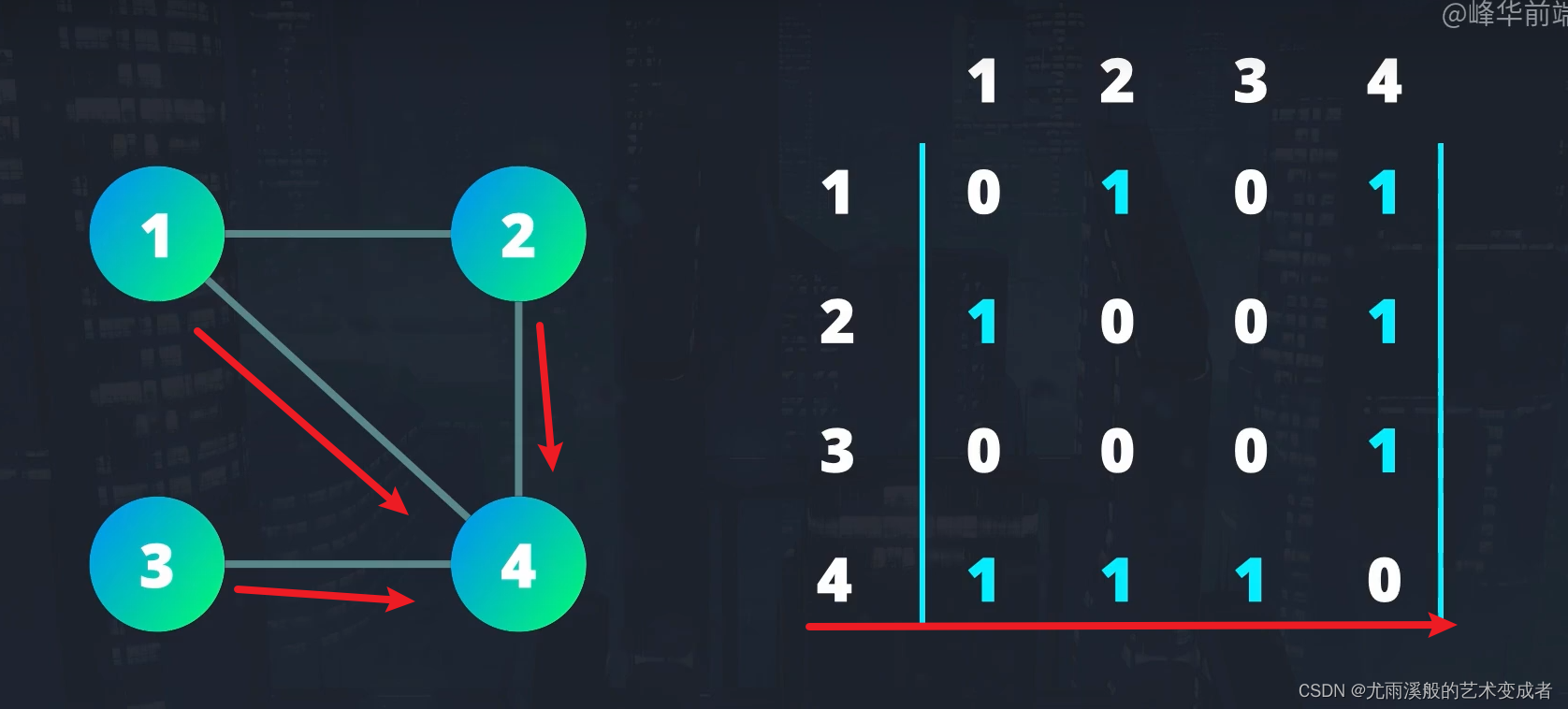
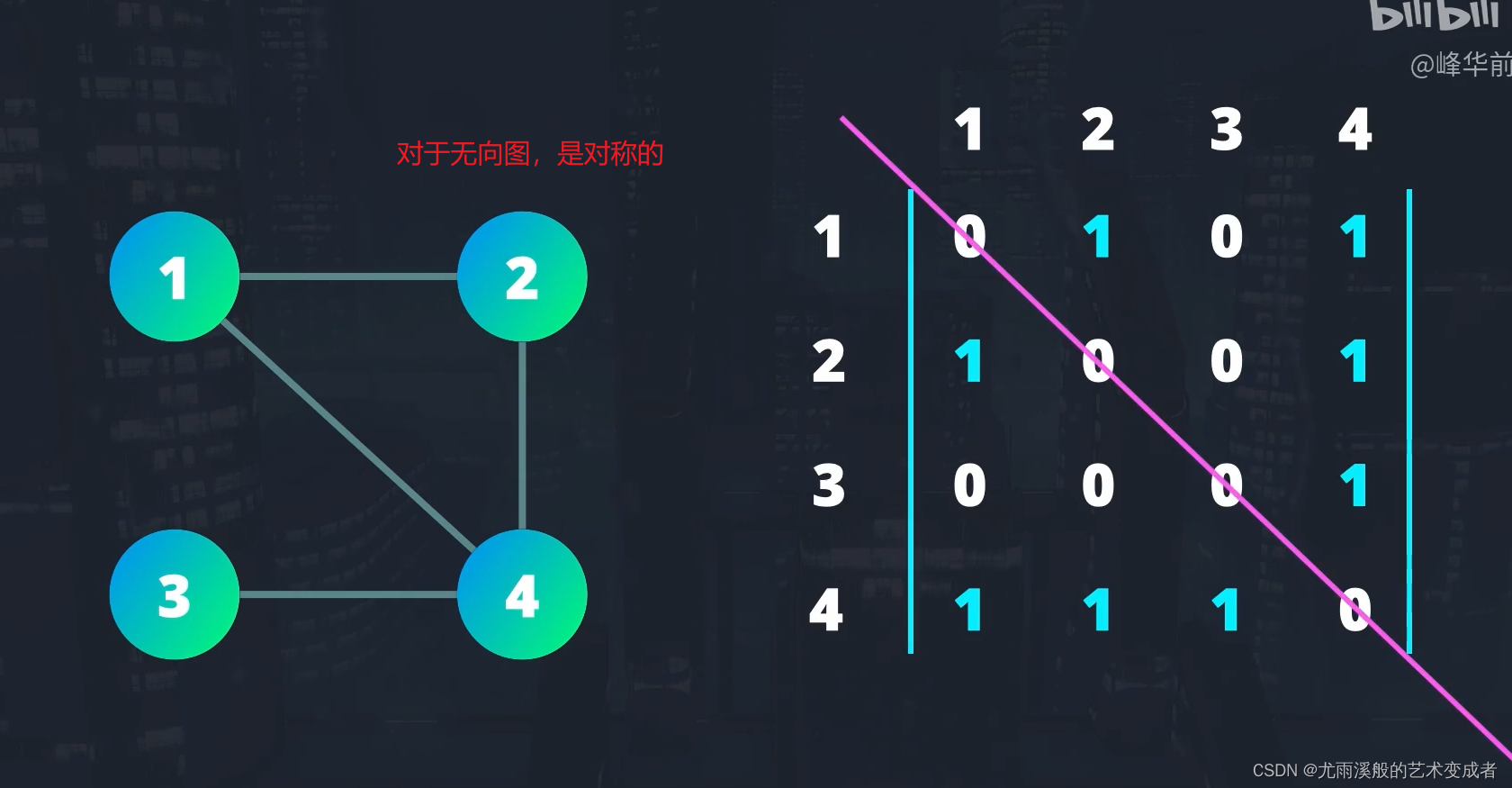
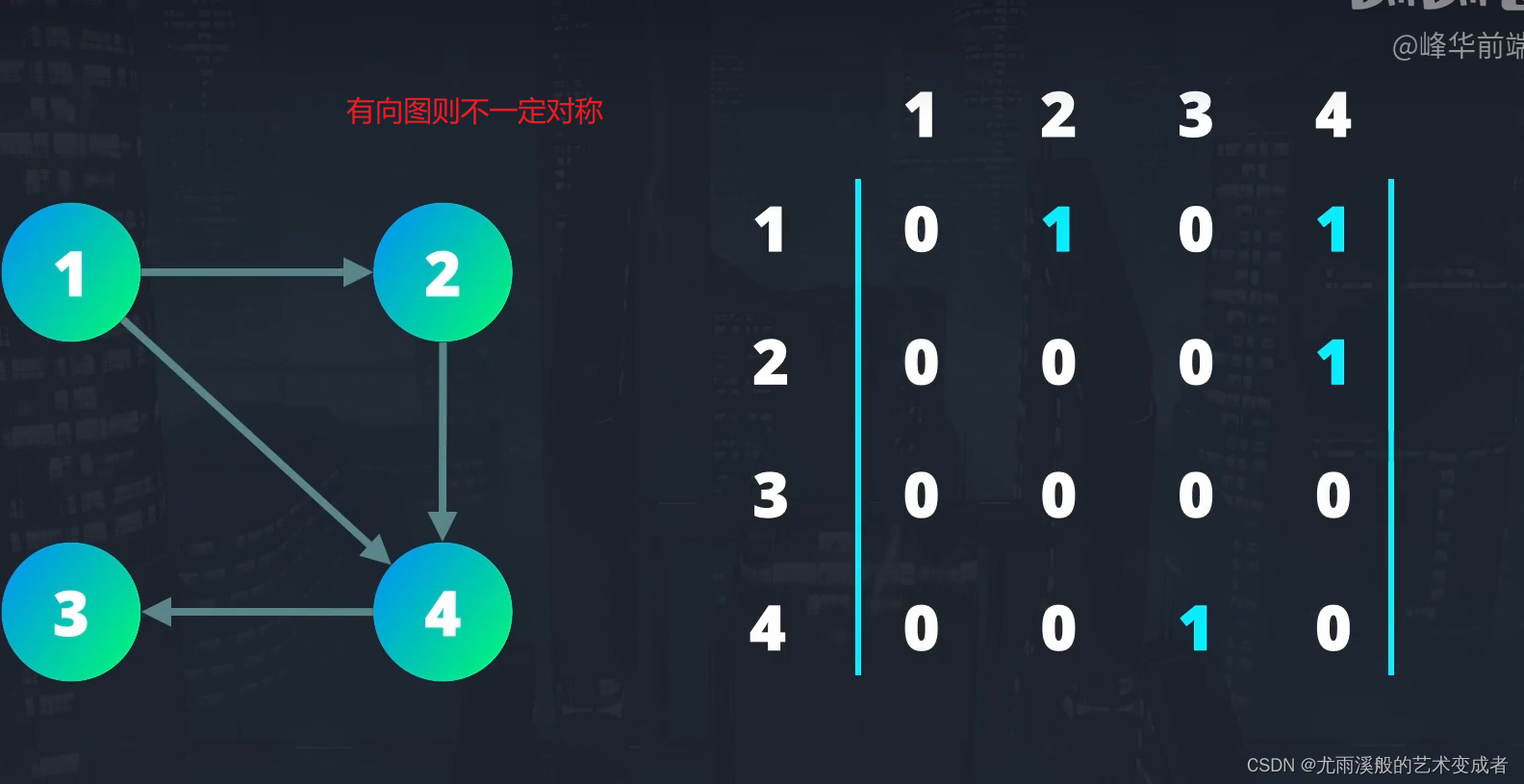
使用邻接节点数组
二叉树的遍历
遍历二叉树是指从根节点开始,访间树中所有的节点。它是其它一些算法的基础,例如深度优先搜索。
遍历二叉树是指从根节点开始,访间树中所有的节点。它是其它一些算法的基础,例如深度优先搜索。
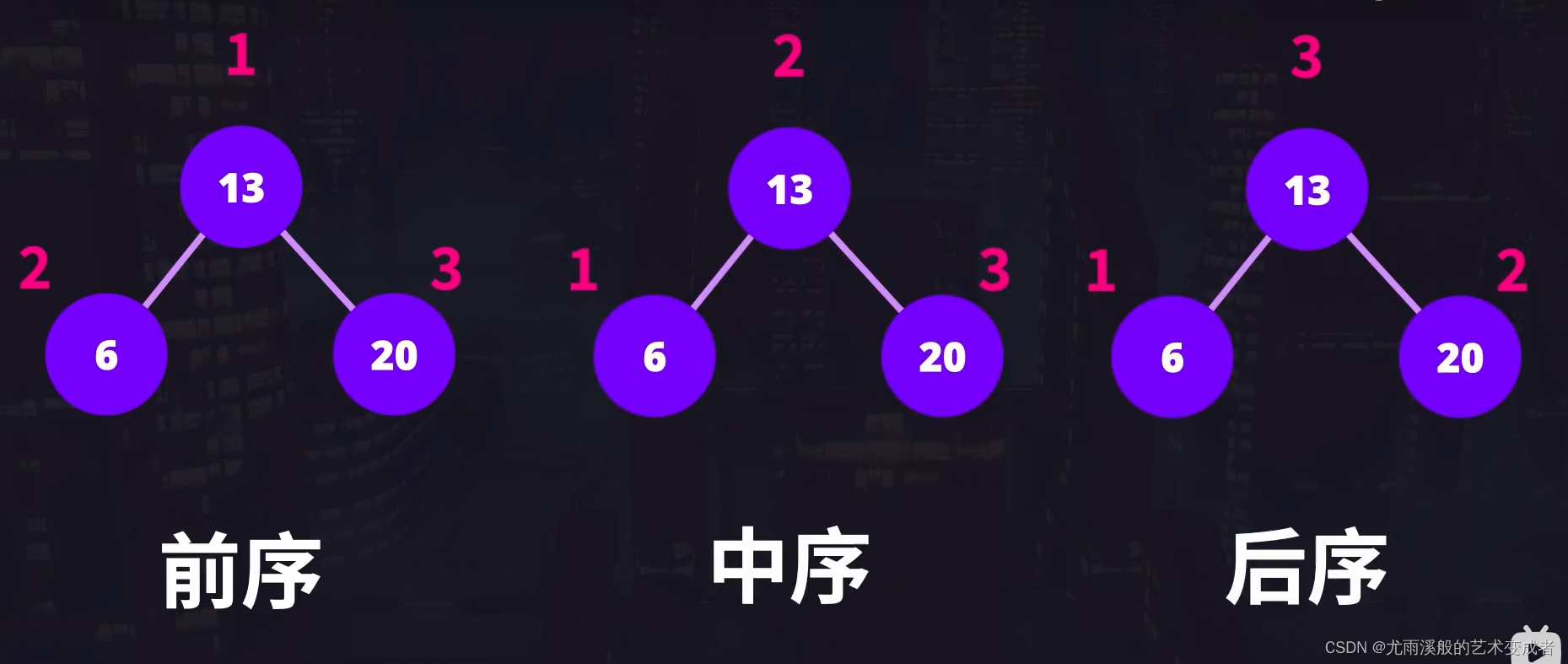
对于二叉树、每个节点有左右两个子节点,对于是先访问左子节点、还是当前节点,或是右子节点,可以把遍历分为前序中序和后序三种。接下来我们分别看一下这三种形式。
先看前序遍历,前序遍历会先访问当前节点的值,之后访问左子节点或右子节点,这里假定先访问左子节点,然后再访问右子节点,对于每个子节点都是做同样的操作。
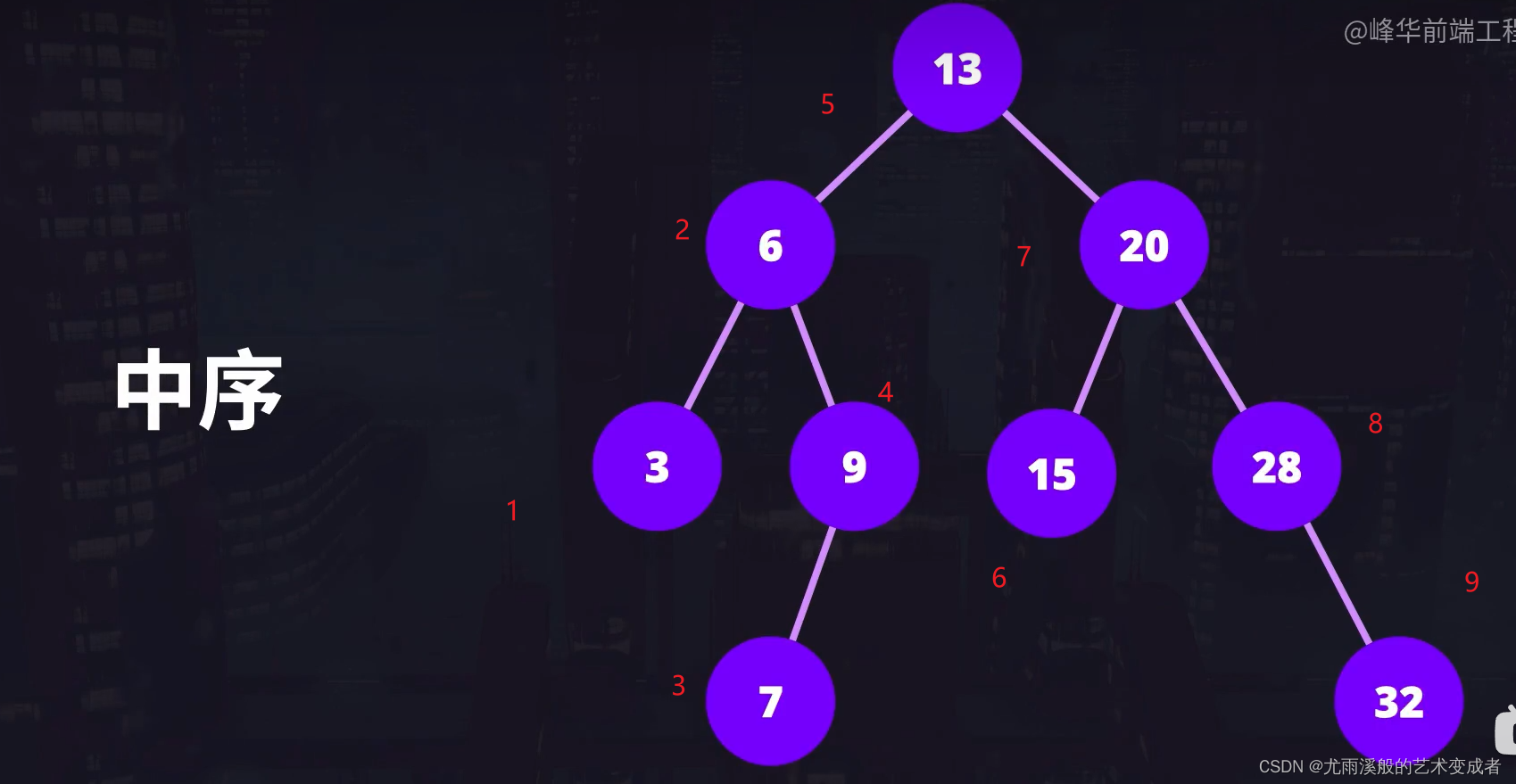
中序遍历则是先访问左子节点,再访问当前节点,最后访问右子节点,对于每个子节点也是重复这个过程。
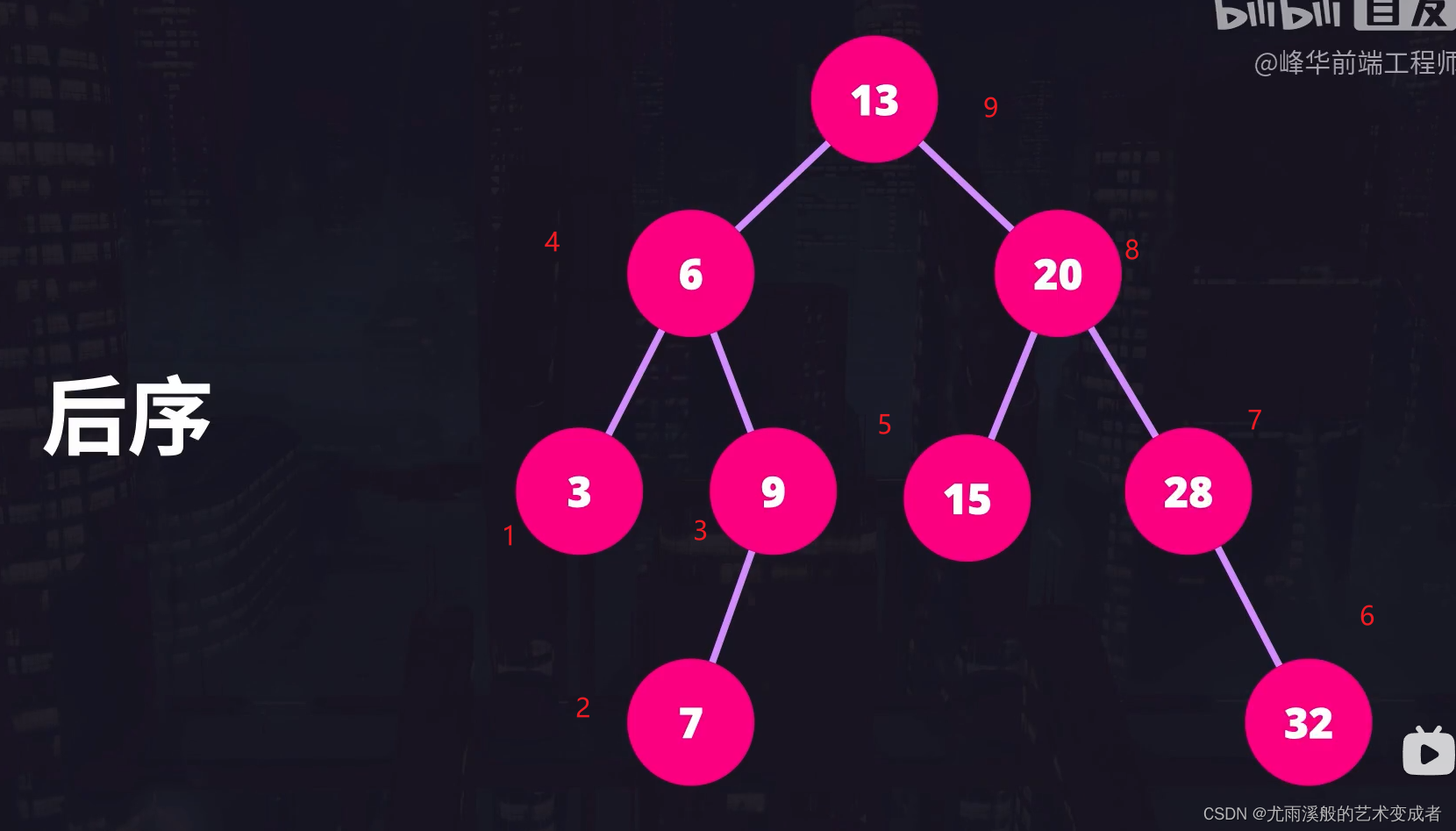
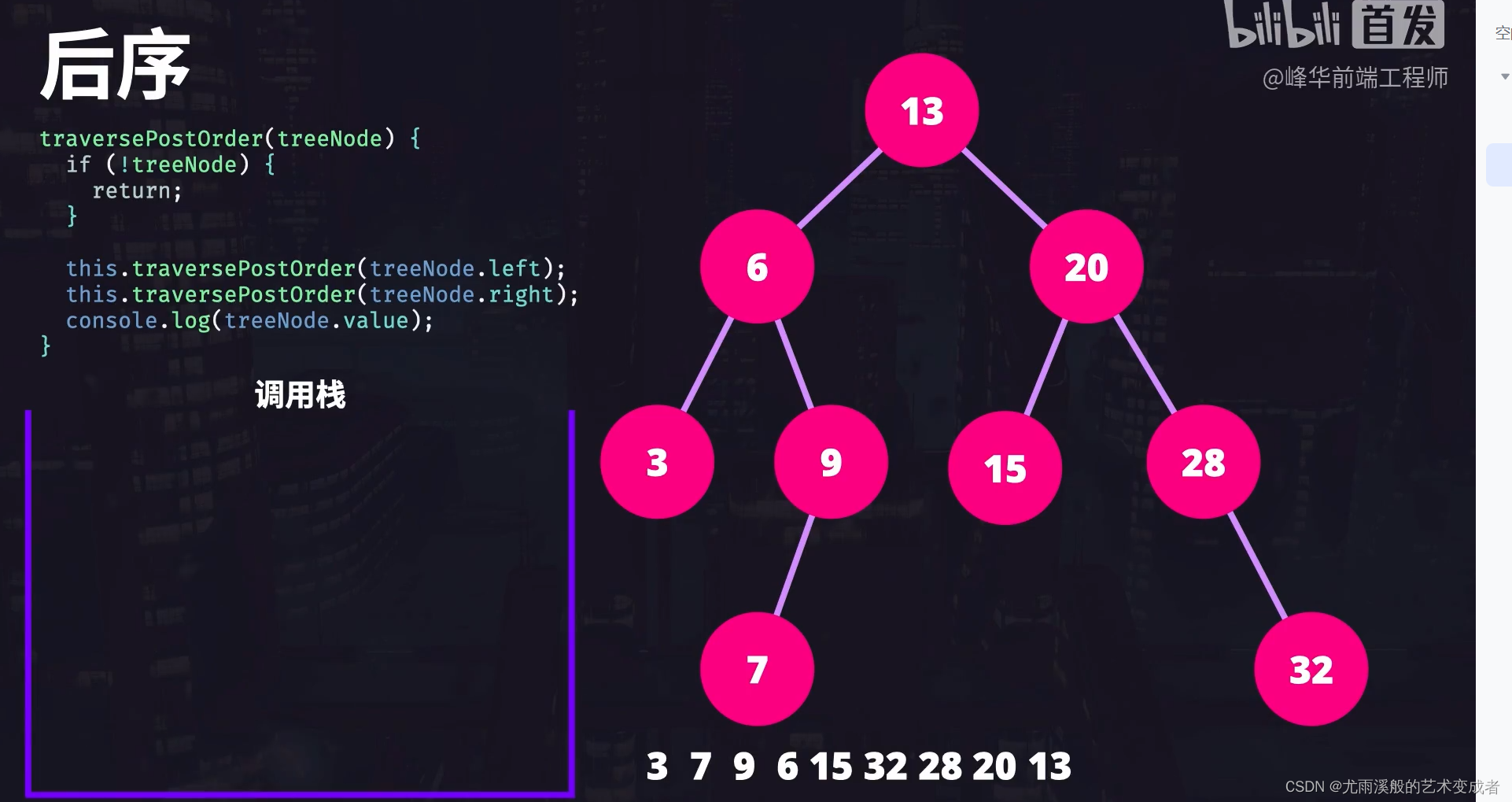
后序遍历则是先访问左子节点的值,再访问右子节点的值,最后访问当前节点的值。对于每个子节点也是同样的操作。
二叉树遍历的代码实现,最简单直观的方法就是使用递归。
对于前序遍历,我们先打印出当前节点的值,然后递归的调用自己,传递左节点,再调用自己传递右节点。当子节点为 null 时退出递归。
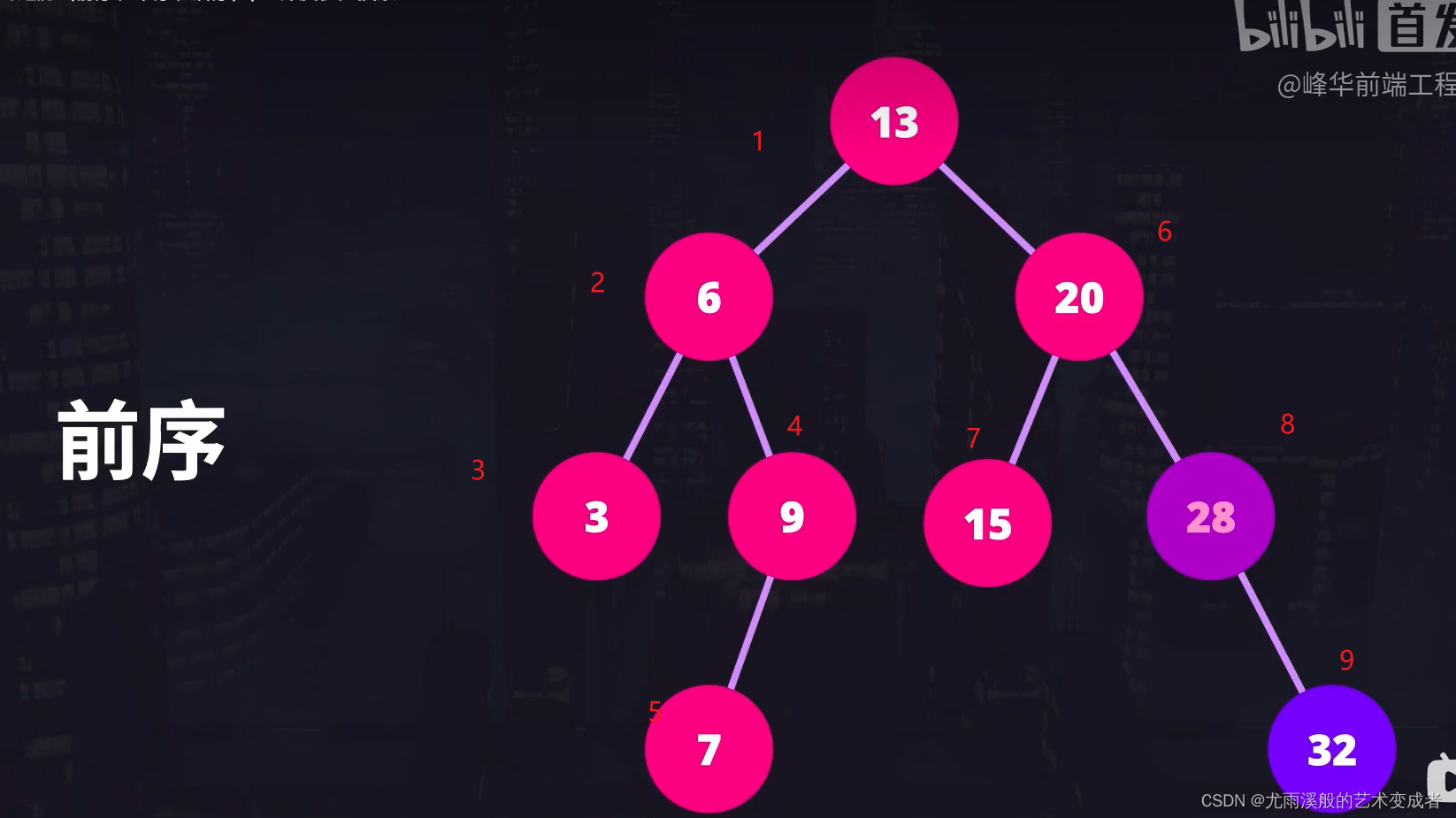
二叉树的前序遍历
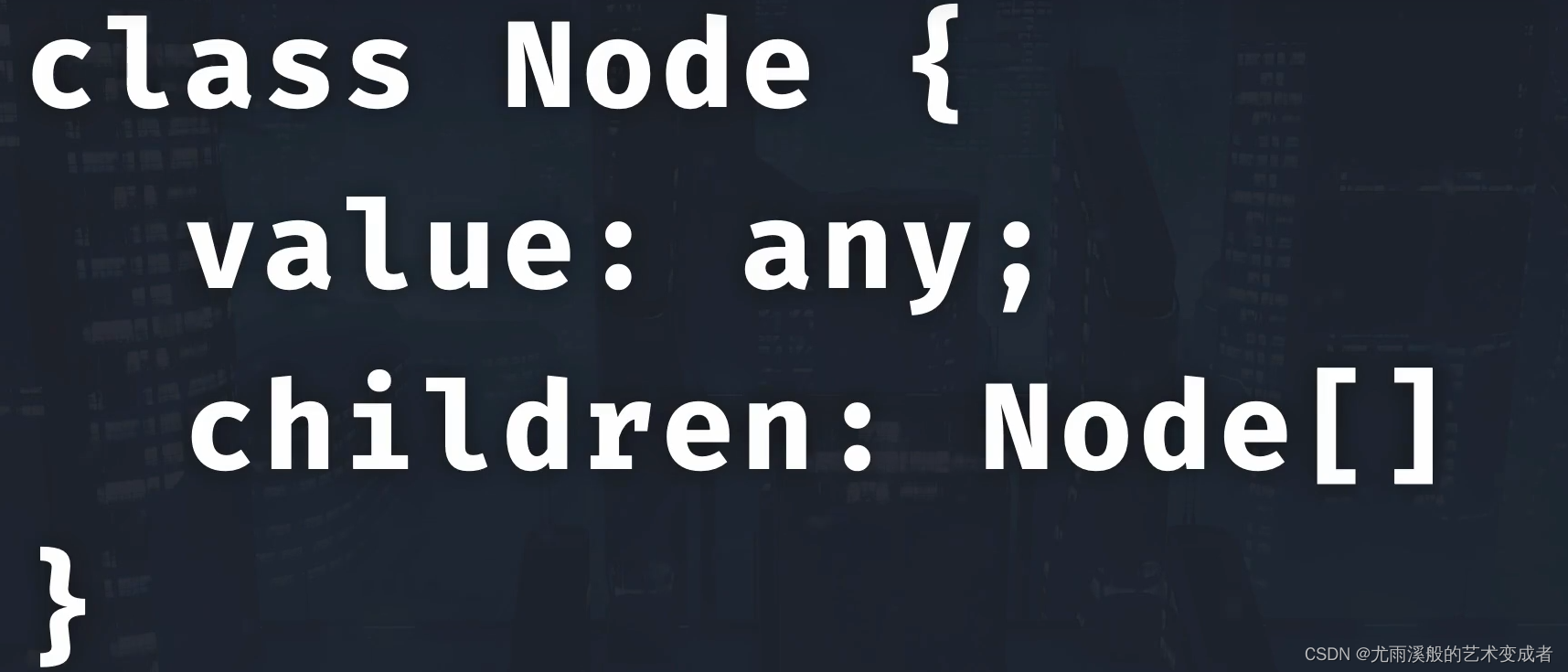
function Node(value) {
this.value = value;
this.leftChild = null;
this.rightChild = null;
}
var a = new Node("a");
var b = new Node("b");
var c = new Node("c");
var d = new Node("d");
var e = new Node("e");
var f = new Node("f");
var g = new Node("g");
a.leftChild = c;
a.rightChild = b;
c.leftChild = f;
c.rightChild = g;
b.leftChild = d;
b.rightChild = e;
function qianxubianli(Node) {
if (Node === null) return;
console.log(Node.value)
qianxubianli(Node.leftChild)
qianxubianli(Node.rightChild)
}
qianxubianli(a)
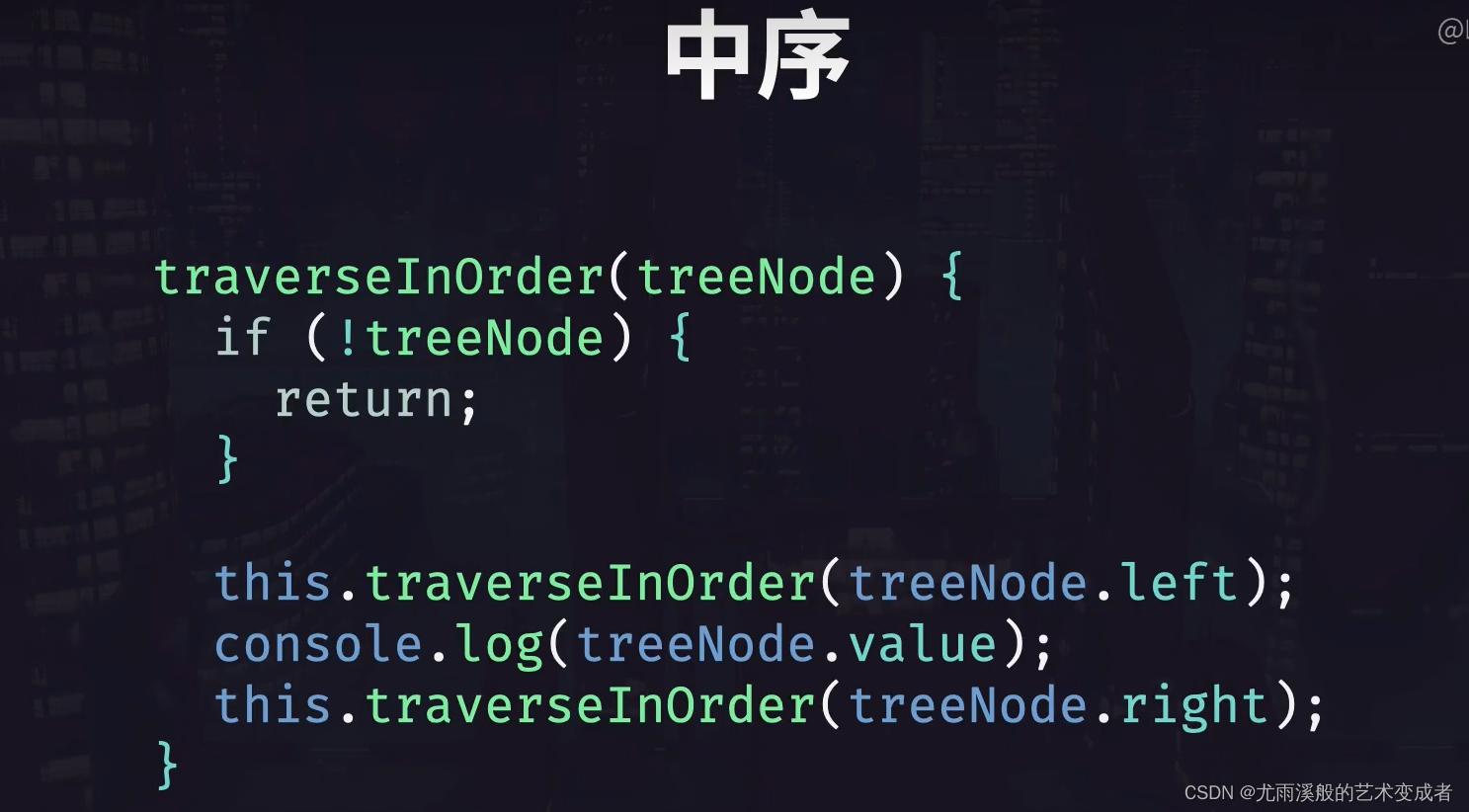
中序遍历
前面相同的Node设置就不重复写了。
function zhongxubianli(Node) {
if (Node === null) return;
zhongxubianli(Node.leftChild);
console.log(Node.value);
zhongxubianli(Node.rightChild)
}
zhongxubianli(a)
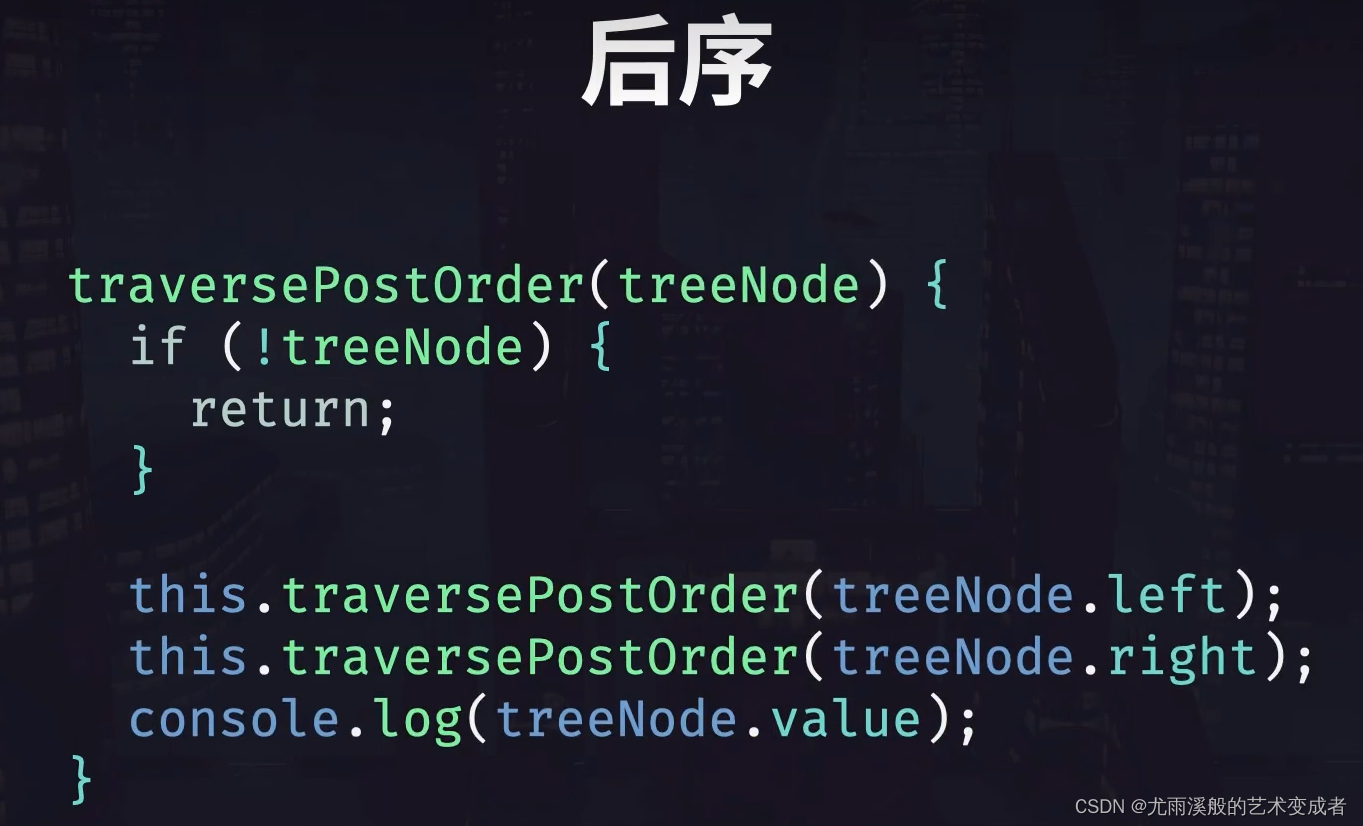
后序遍历
function houxubianli(Node) {
if (Node === null) return;
houxubianli(Node.leftChild);
houxubianli(Node.rightChild)
console.log(Node.value);
}
houxubianli(a)
根据前序遍历、中序遍历获得二叉树
function Node(value) {
this.value = value;
this.leftChild = null;
this.rightChild = null;
}
const qianxu = ["a", "c", "f", "g", "b", "d", "e"];
const zhongxu = ["f", "c", "g", "a", "d", "b", "e"];
function fn(qianxu, zhongxu) {
if (qianxu == null || zhongxu == null || qianxu.length == 0 || zhongxu.length == 0 || qianxu.length !== zhongxu.length) return;
var root = new Node(qianxu[0])
var index = zhongxu.indexOf(root.value);
var qianxuLeft = qianxu.slice(1, index + 1);
var qianxuRight = qianxu.slice(index + 1, qianxu.length);
var zhongxuLeft = zhongxu.slice(0, index);
var zhongxuRight = zhongxu.slice(index + 1, zhongxu.length);
root.leftChild = fn(qianxuLeft, zhongxuLeft);
root.rightChild = fn(qianxuRight, zhongxuRight);
return root;
}
var root = fn(qianxu, zhongxu);
console.log(root.leftChild)
console.log(root.rightChild)
根据中序遍历、后序遍历获得二叉树
function Node(value) {
this.value = value;
this.leftChild = null;
this.rightChild = null;
}
const zhongxu = ["f", "c", "g", "a", "d", "b", "e"];
const houxu = ["f", "g", "c", "d", "e", "b", "a"];
function fn(houxu, zhongxu) {
if (houxu == null || zhongxu == null || houxu.length == 0 || zhongxu.length == 0 || houxu.length !== zhongxu.length) return;
var root = new Node(houxu[houxu.length - 1]);
var index = zhongxu.indexOf(root.value);
var houLeft = houxu.slice(0, index);
var houRight = houxu.slice(index, houxu.length - 1);
var zhongLeft = zhongxu.slice(0, index);
var zhongRight = zhongxu.slice(index + 1, zhongxu.length);
root.leftChild = fn(houLeft, zhongLeft);
root.rightChild = fn(houRight, zhongRight);
return root;
}
var root = fn(houxu, zhongxu);
console.log(root.leftChild)
console.log(root.rightChild)
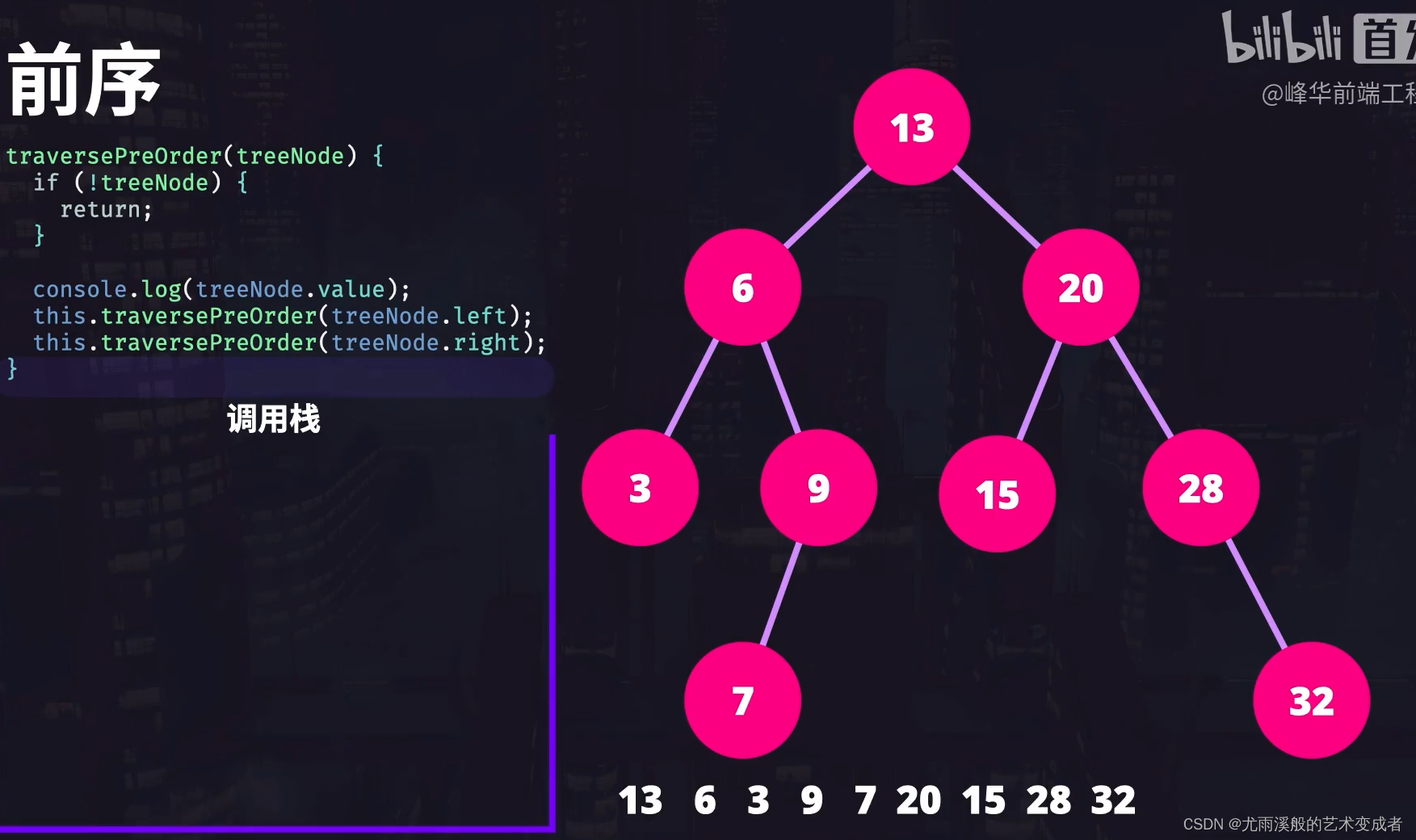
前序遍历
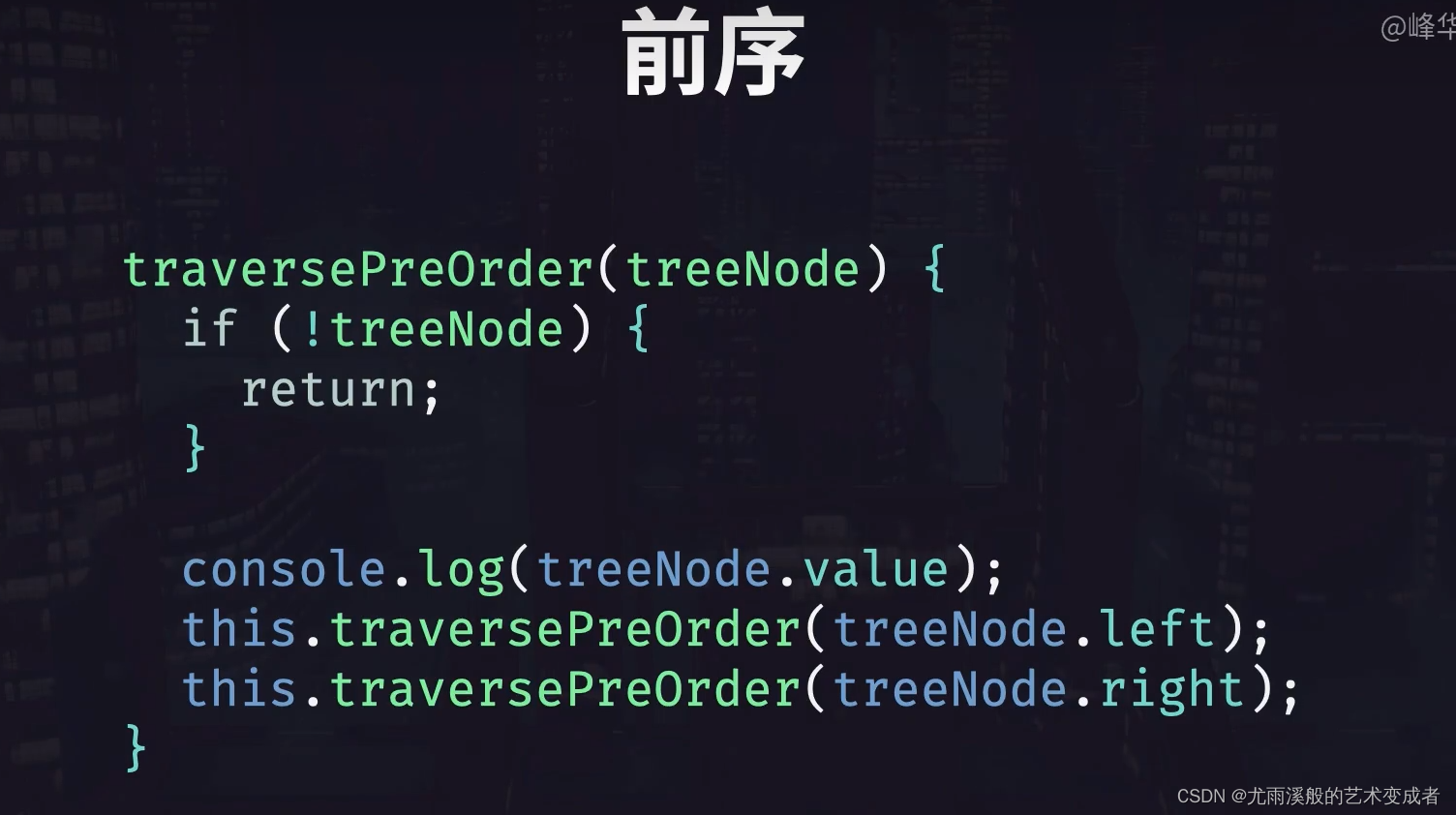
压入调用栈—执行完代码开始出栈
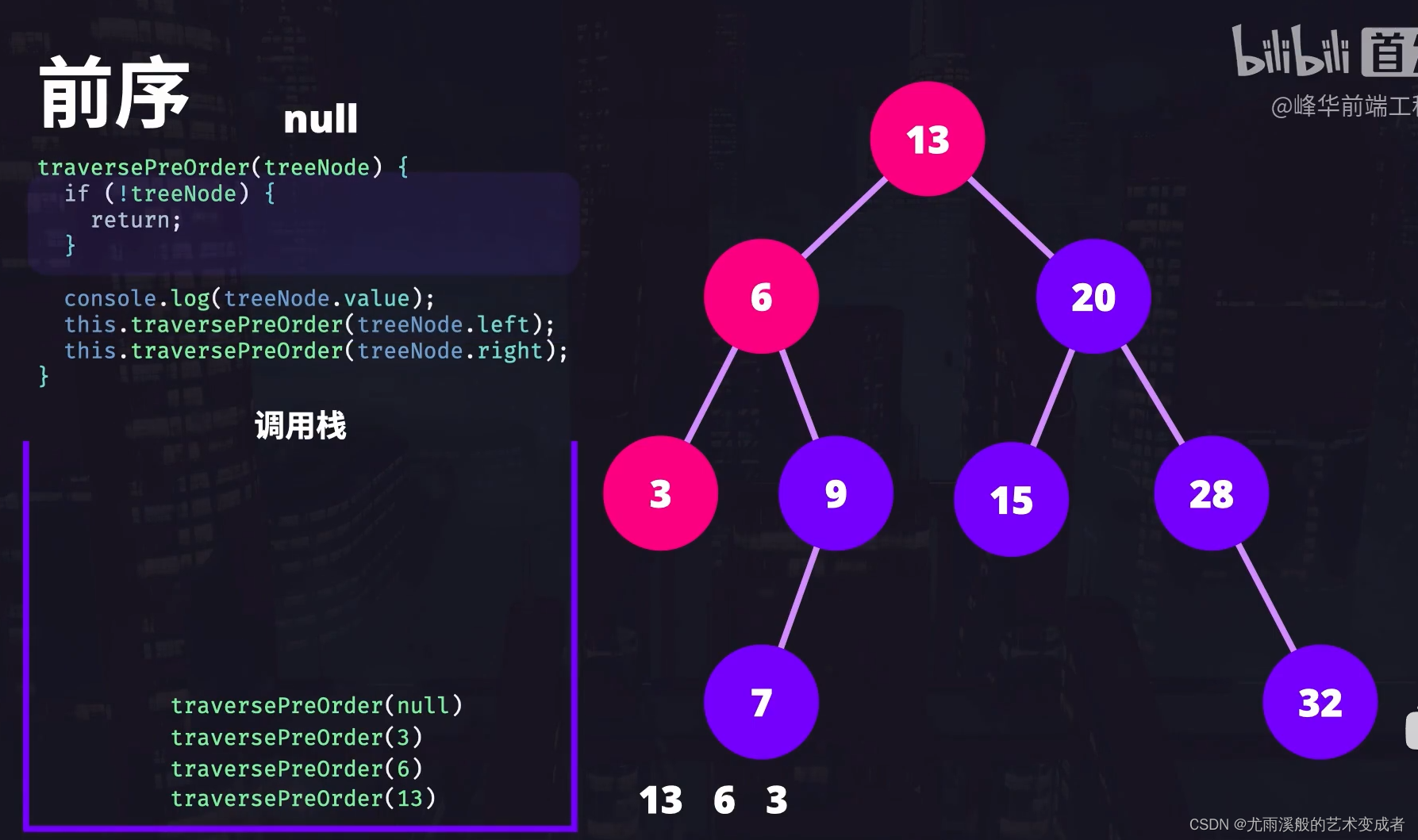
代码:
调用 traversePreOrder() 遍历 root | [traversePreOrder(13)]
第一行先打印出根节点的值 13。| [traversePreOrder(13)]
接下来,执行到遍历左节点的方法 traversePreOrder(6),放入调用栈并执行,打印出 6,此时因为遍历左节点的方法还未 return,所以遍历右子节点的函数调用还不能执行 | 调用栈:[traversePreOrder(6), traversePreOrder(13)]。
接着,递归调用 traversePreOrder() 遍历 6 的左子节点,函数压入调用栈并执行,打印出 3 | 调用栈:[traversePreOrder(3), traversePreOrder(6), traversePreOrder(13) ]。
接着递归调用 traversePreOrder(treeNode.left) 遍历 3 的左子节点|调用栈:[traversePreOrder(null),traversePreOrder(3), traversePreOrder(6) , traversePreOrder(13)]
此时,执行 traversePreOrder(null),treeNode 为 null,函数执行到 if 后,直接 return 了|调用栈:[traversePreOrder(3), traversePreOrder(6) , traversePreOrder(13)]
那么接下来就从调用栈拿出最顶部的函数 traversePreOrder(3),继续执行,调用 traversePreOrder(treeNode.right) |调用栈:[traversePreOrder(null), traversePreOrder(3), traversePreOrder(6) , traversePreOrder(13)]
treeNode.right 也是 null,所以函数直接返回 |调用栈:[ traversePreOrder(3), traversePreOrder(6) , traversePreOrder(13)]。
接着继续执行 traversePreOrder(3),后面没有代码了,所以 traversePreOrder(3) 函数返回。| [ traversePreOrder(6) , traversePreOrder(13)]
接着执行 traversePreOrder(6),调用它里边的 traversePreOrder(treeNode.right) | [traversePreOrder(9), traversePreOrder(6) , traversePreOrder(13)]。
执行打印出 9 | 调用栈 [traversePreOrder(9), traversePreOrder(6) , traversePreOrder(13)]。
接着调用 9 里的 traversePreOrder(treeNode.left) | [traversePreOrder(7), traversePreOrder(9), traversePreOrder(6) , traversePreOrder(13)]。
执行打印出 7。后面它没有子节点,所以它里边的 traversePreOrder(treeNode.left) 和 traversePreOrder(treeNode.right) 直接返回,这里就不演示,它本身到这里也执行结束了。| [traversePreOrder(9), traversePreOrder(6) , traversePreOrder(13)]。
又回到节点 9,它没有右节点,所以也执行结束并返回。| [traversePreOrder(6) , traversePreOrder(13)]。
到了 traversePreOrder(6),它的代码也执行完毕了,返回。| [ traversePreOrder(13)]
现在开始继续执行 13 根节点的 traversePreOrder(treeNode.right) 方法了,这里边的执行顺序和之前一样,我们简单过一下。
调用 traversePreOrder(20) 打印出 20 | [traversePreOrder(20), traversePreOrder(13)]。
遍历左节点并打印出 15。 | [traversePreOrder(15), traversePreOrder(20), traversePreOrder(13)]。
15 没有子节点直接返回,遍历 20 的右节点,打印出 28。| [traversePreOrder(28), traversePreOrder(20), traversePreOrder(13)]。
28 没有左子节点,遍历右子节点,打印出 32 并返回。| [traversePreOrder(32), traversePreOrder(20), traversePreOrder(13)]。
20 节点遍历完毕并返回。| [traversePreOrder(13)]。
13 根节点遍历完毕并返回 | []。
此时,前序遍历就完成了,结果是:
13 6 3 9 7 20 15 28 32
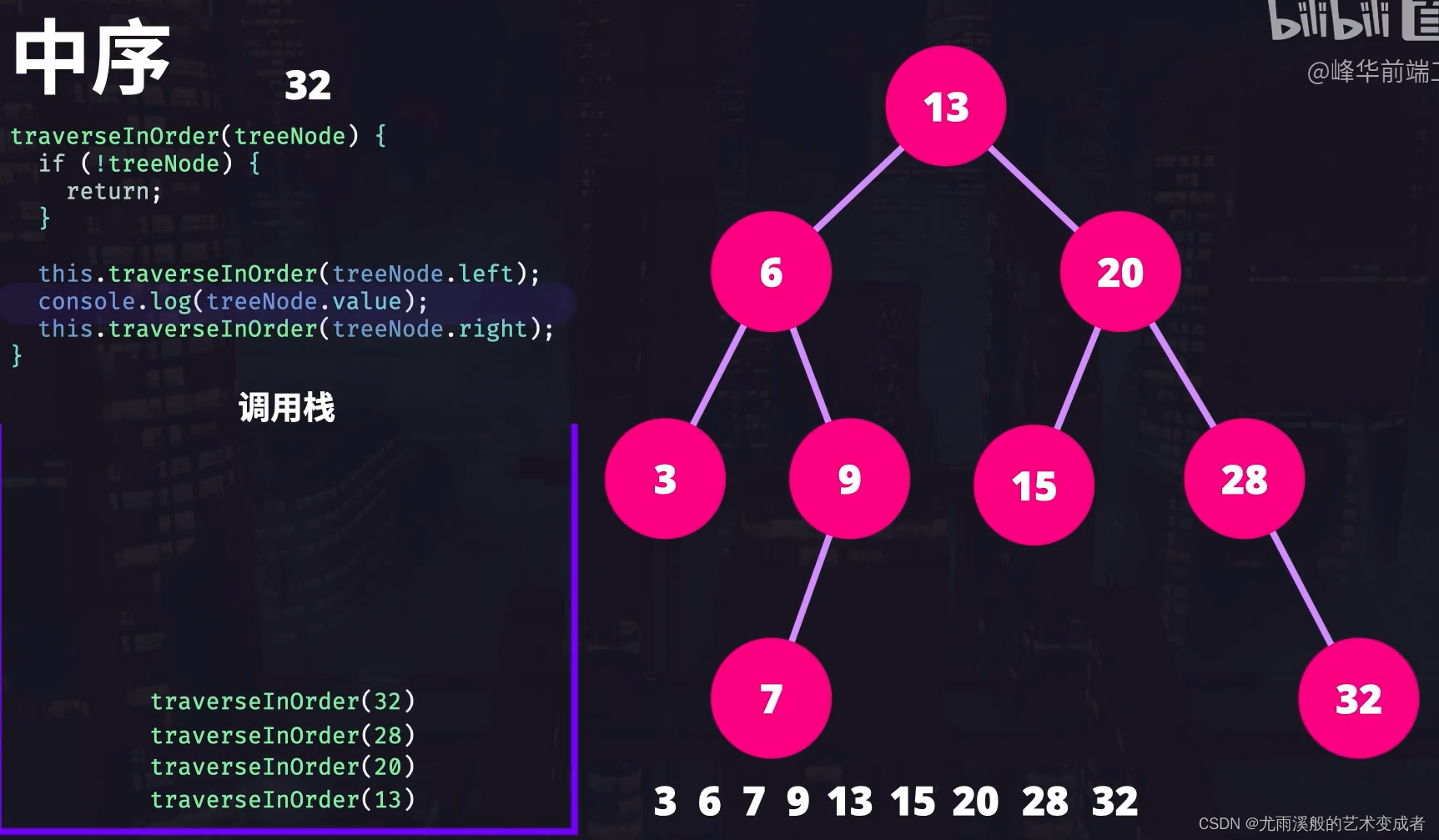
中序遍历
后续遍历
O 表示法

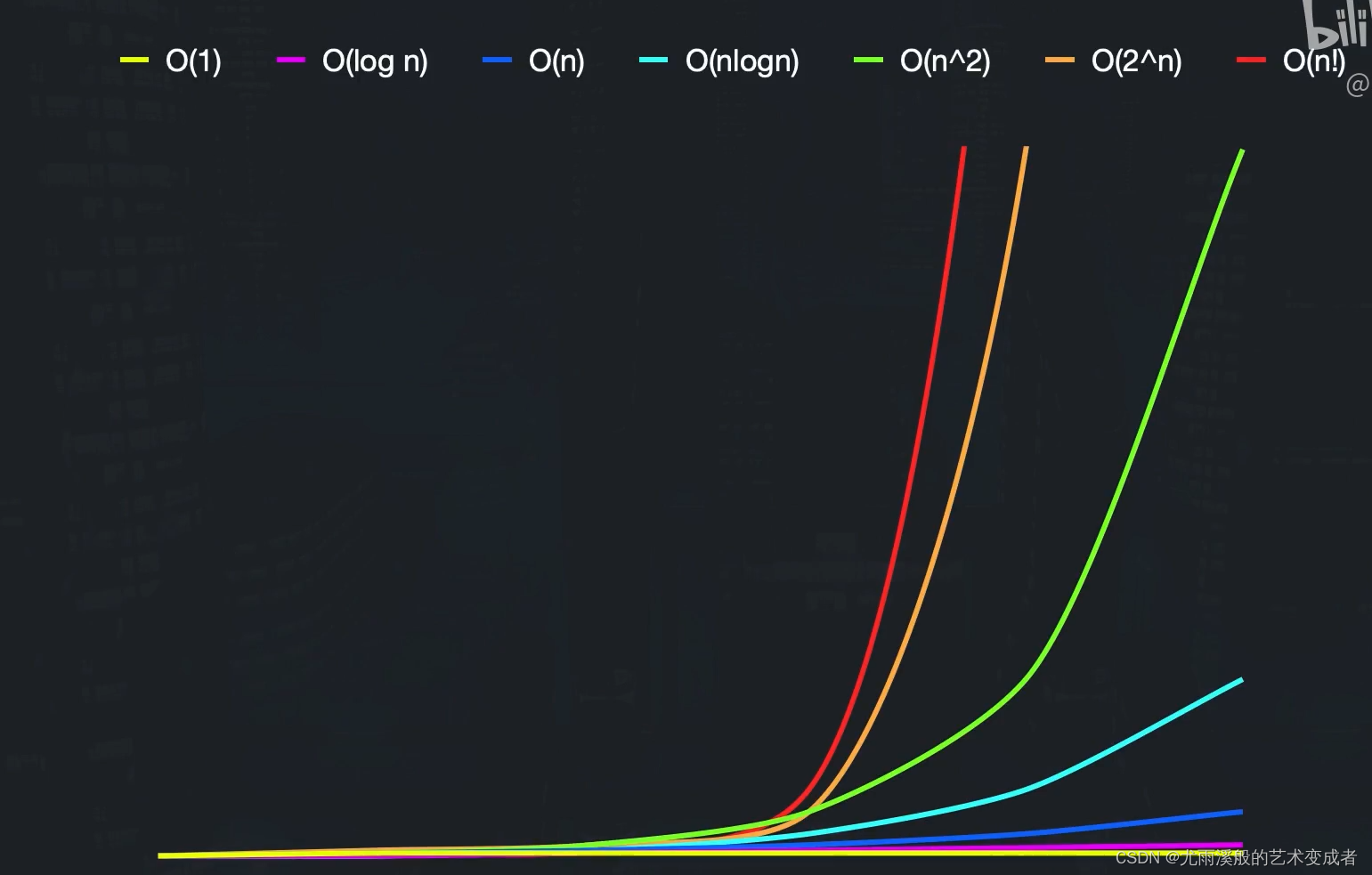


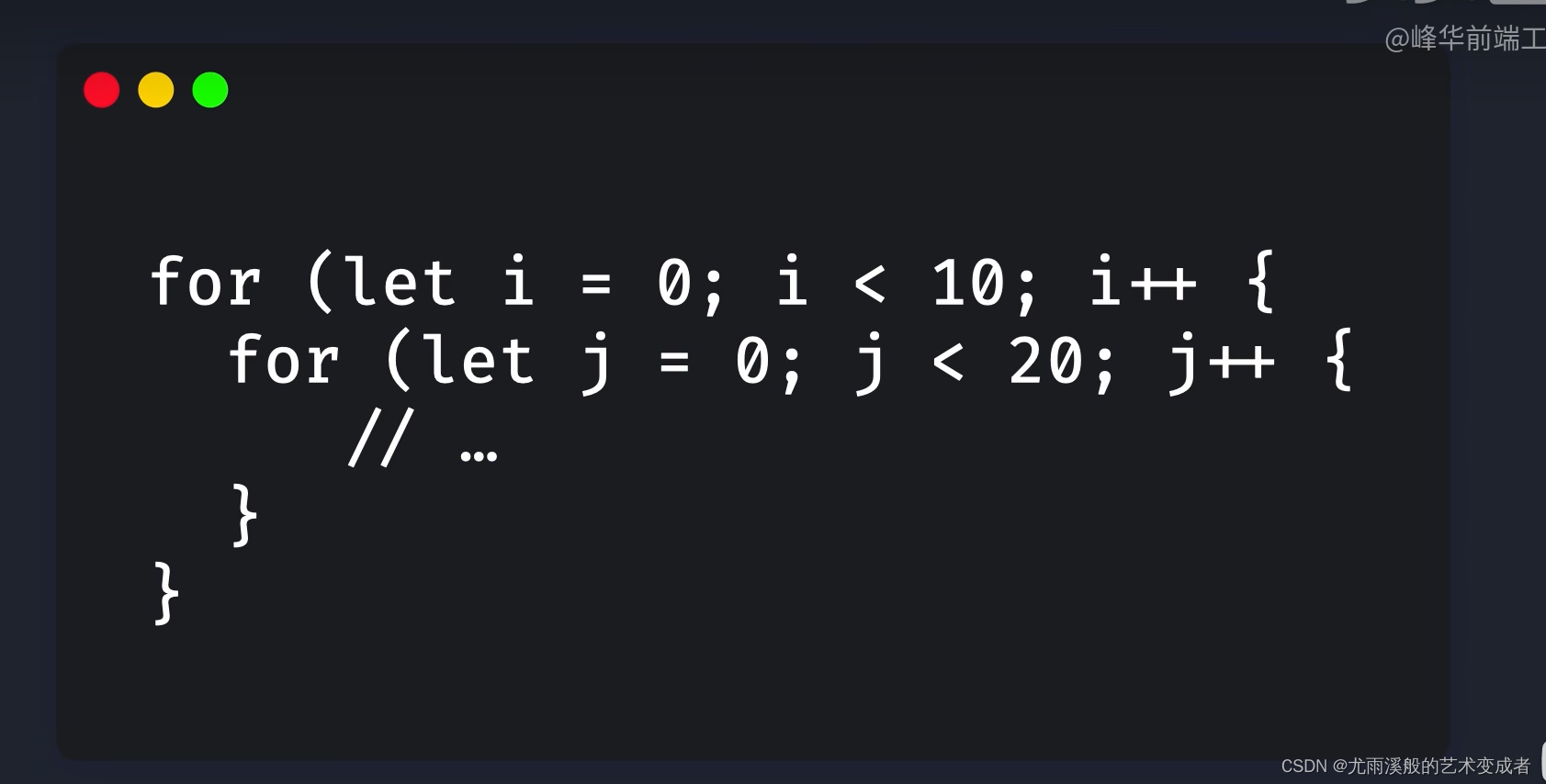
大 O 表示法是粗略的估算算法的效率,会直接忽略常数,例如我们使用平行的两个 for 循环,遍历两次数组,可能直接得出时间复杂度为 O(2N),但是最终我们还是表示为 O(N):

对于无关输入大小,只执行固定行数的代码,无论是 1 行、5 行还是 10 行,都可以认为是 O(1):

对于算法的评价,会分为最佳情况、平均情况和最坏情况,因为有的算法会根据输入数据的不同,会有不同的时间复杂度,大 O 表示法通常表示的是最坏情况。

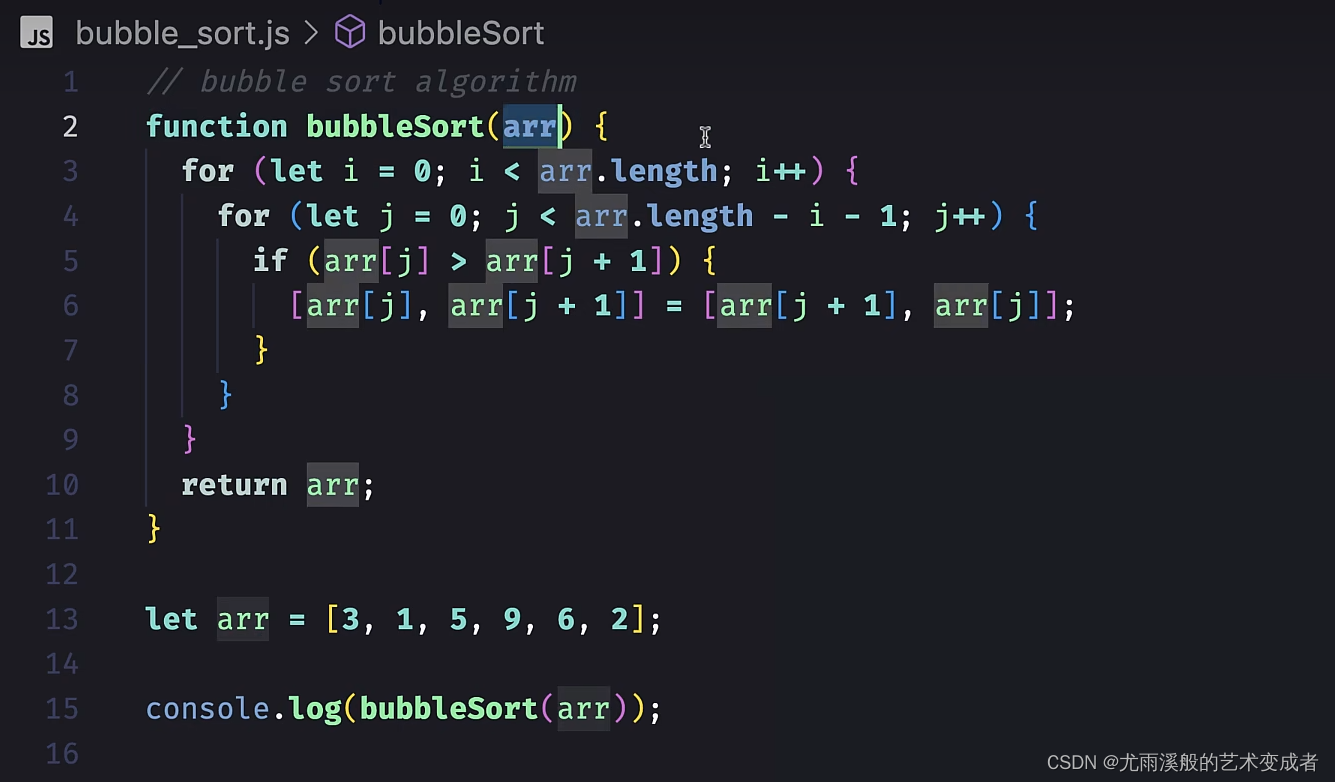
对于空间复杂度,大 O 表示法表示的是算法在执行时,需要额外占用的内存空间,例如对于冒泡排序,它不需要额外创建存储空间,而是就地对原数组进行排序,所以它的空间复杂度是 O(1):

常见算法的时间复杂度
下面列出一些常见算法的时间复杂度:
数组的访问:O(1)
链表的插入和删除:O(1)
数组的查找:O(N)
折半查找:O(logN),因为每次查找都会少 N / 2 数据。
冒泡排序、选择排序、插入排序、快速排序:O(N2)
归并排序:O(NlogN)
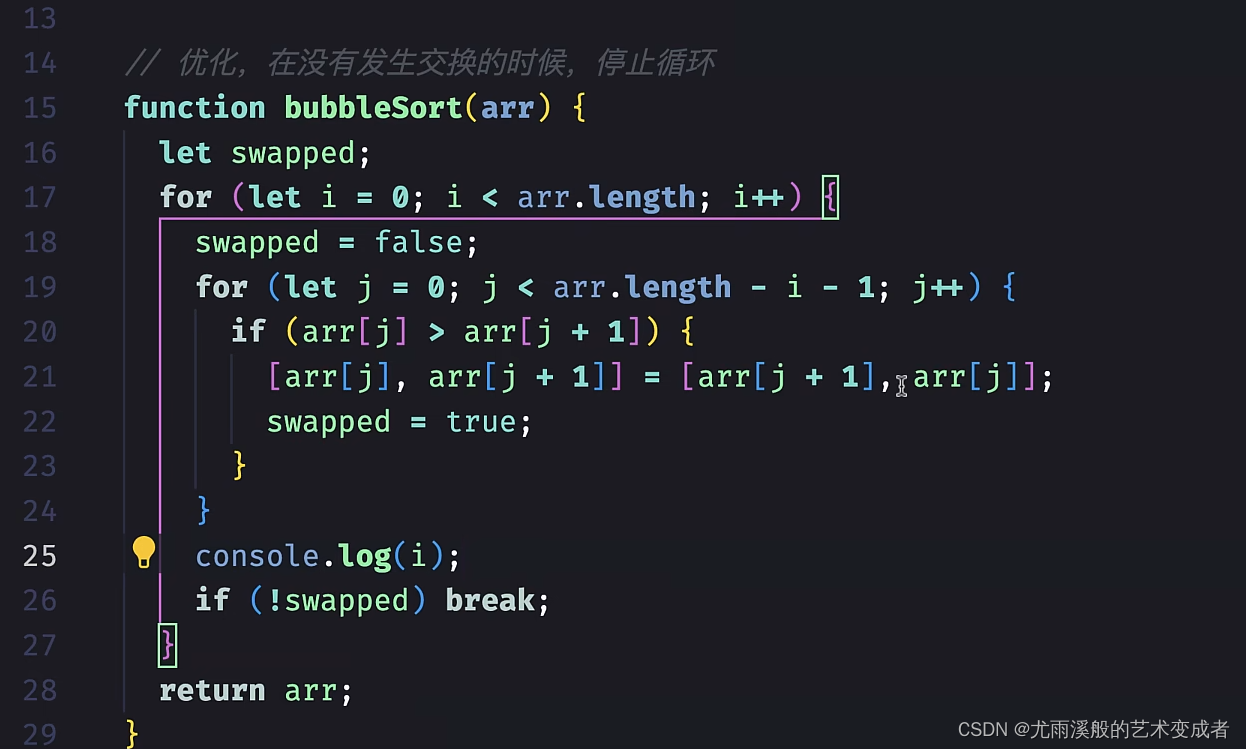
有些算法的时间复杂度并不稳定,例如插入排序、快速排序等。它们会根据原始输入的数组是否已经整体有序,所表现出来的时间复杂度也不相同。例如插入排序在最好情况下的时间复杂度是 O(n)。







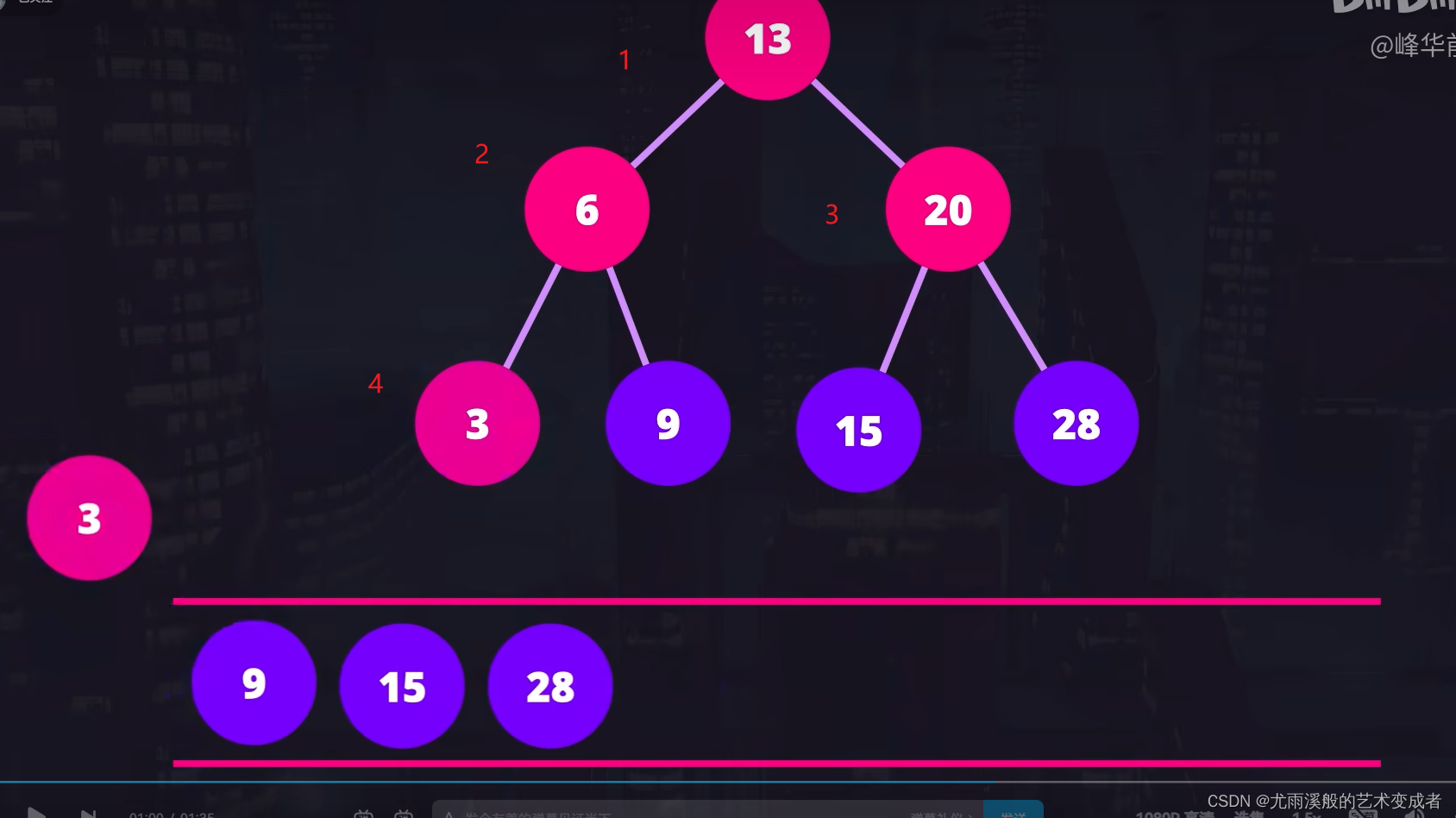
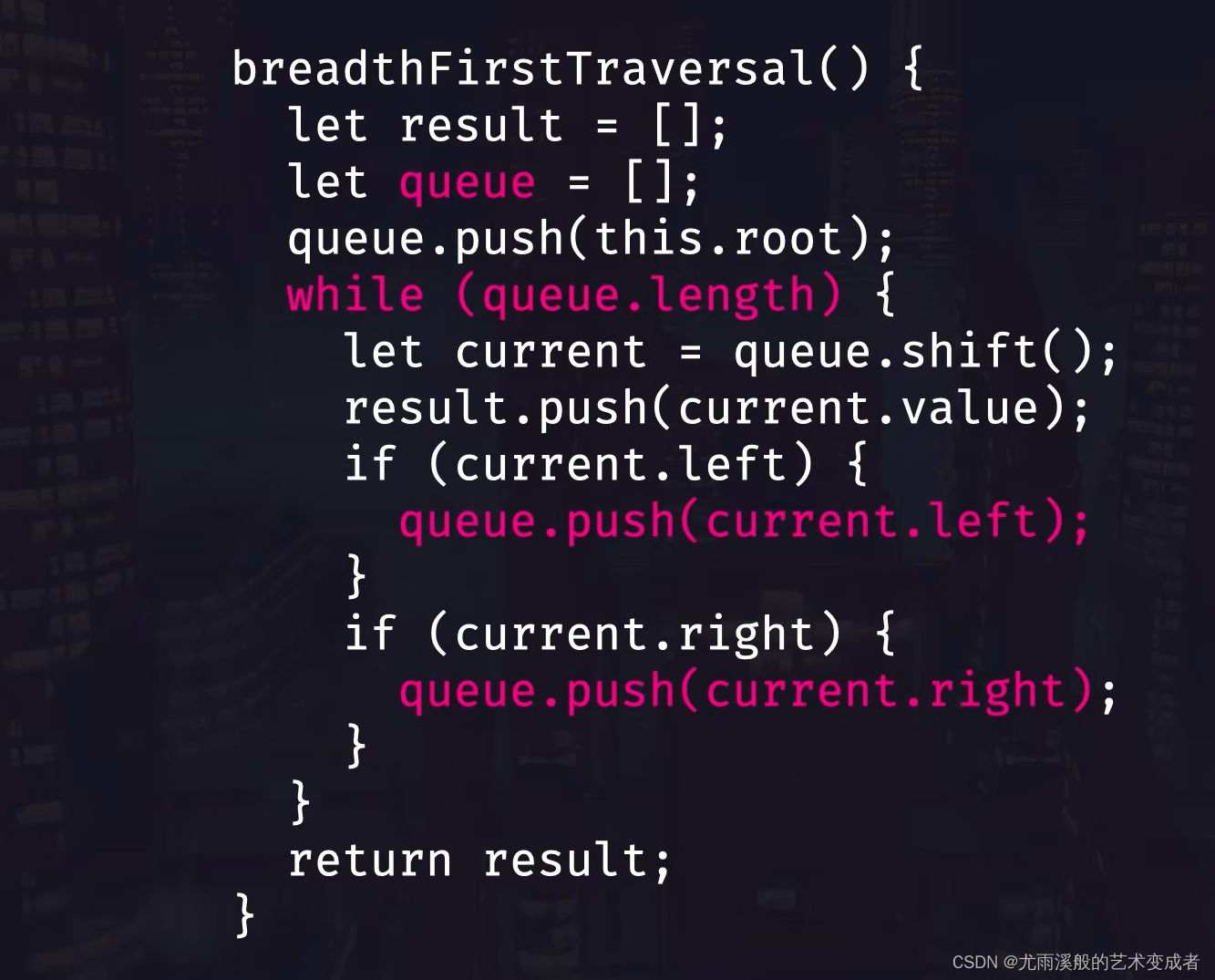
树的广度优先遍历





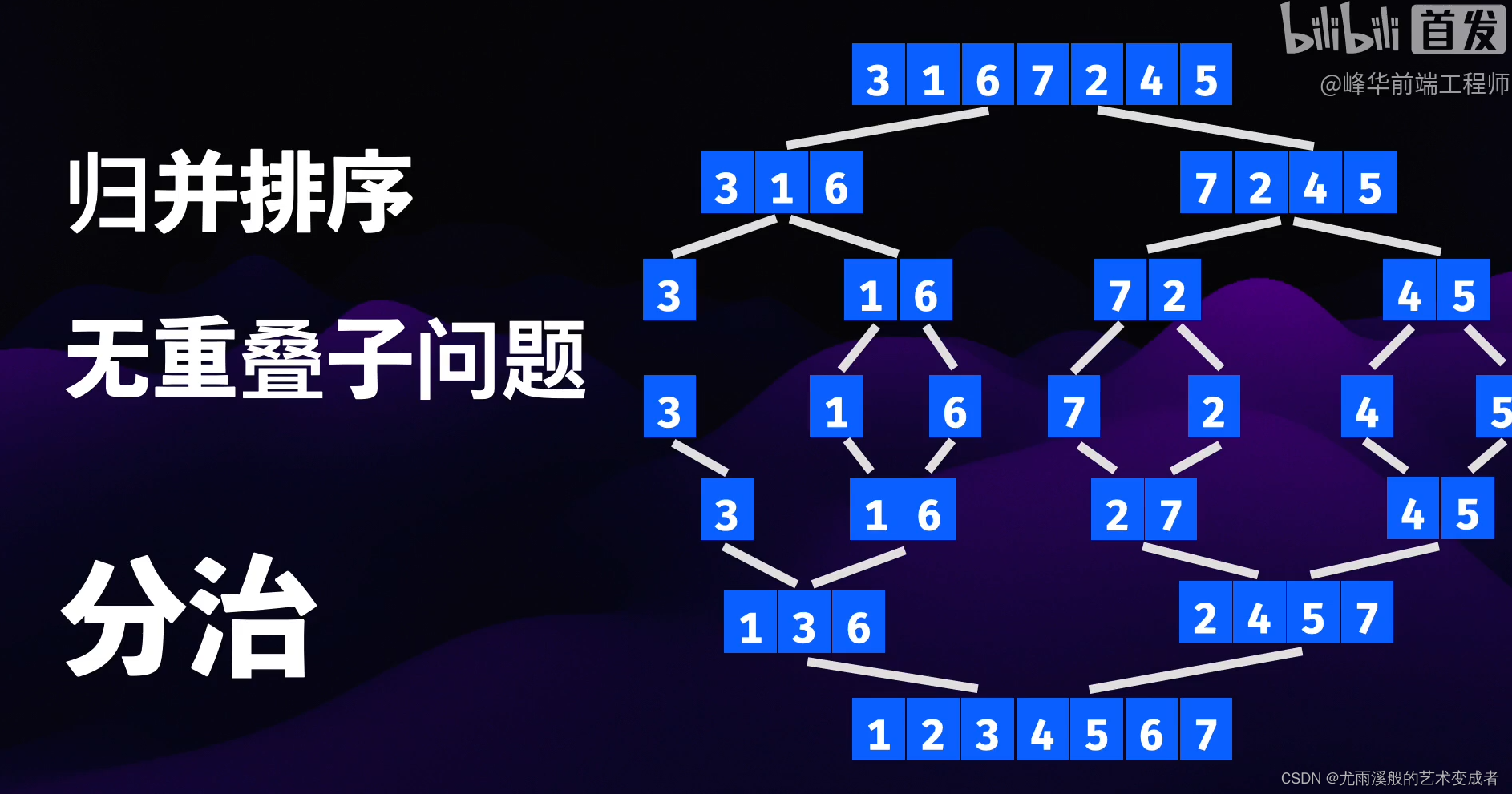
归并排序


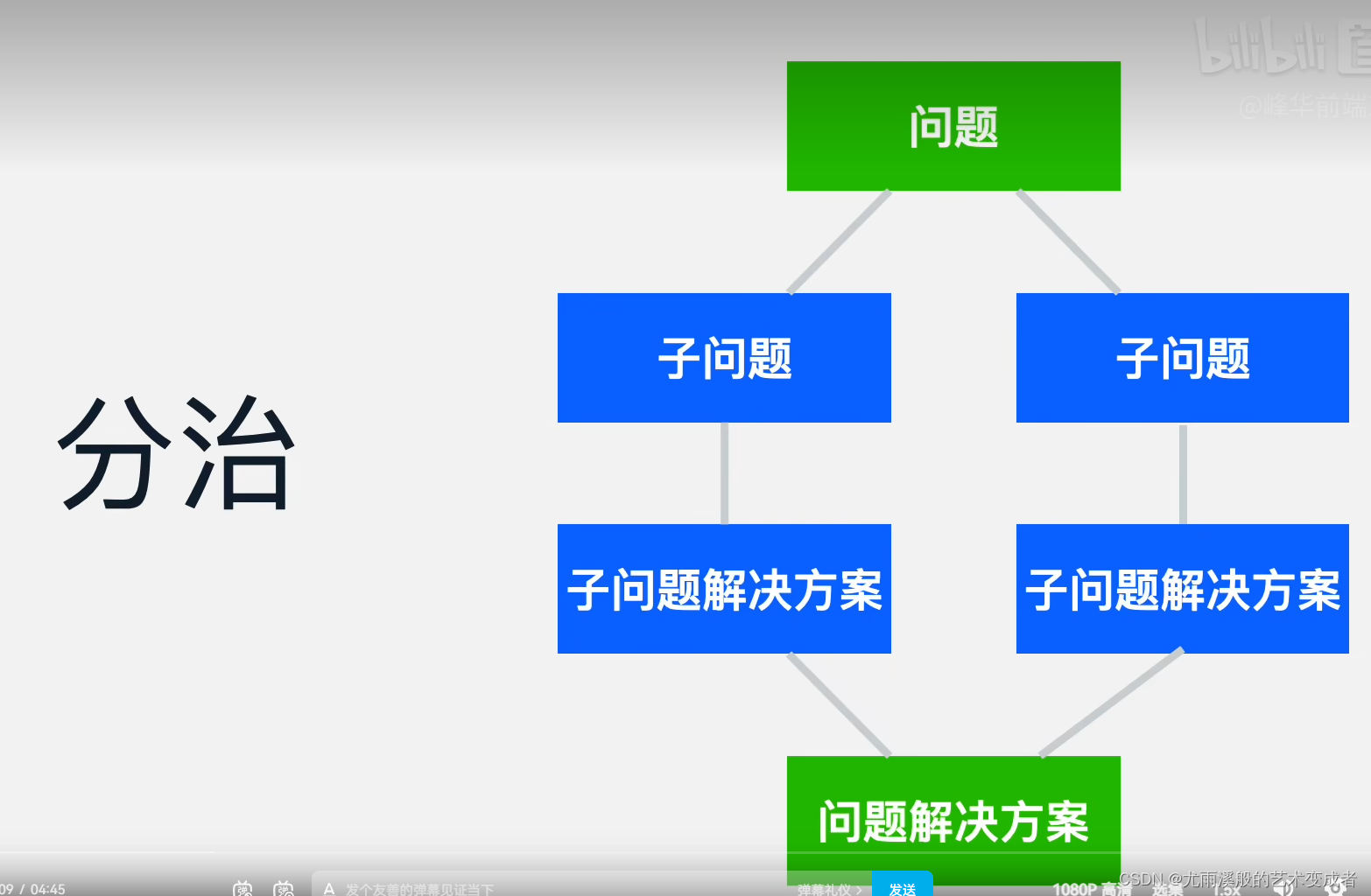
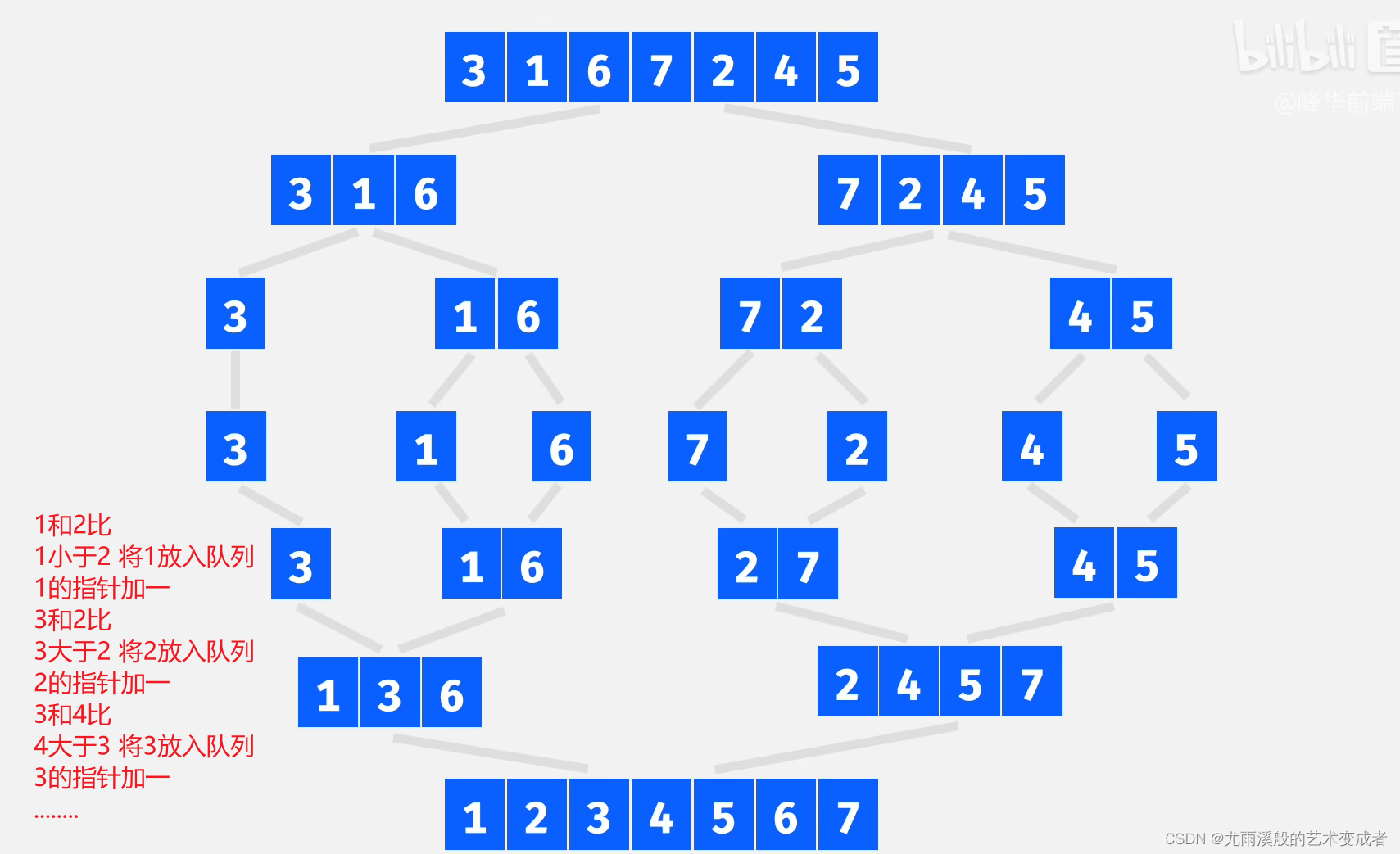

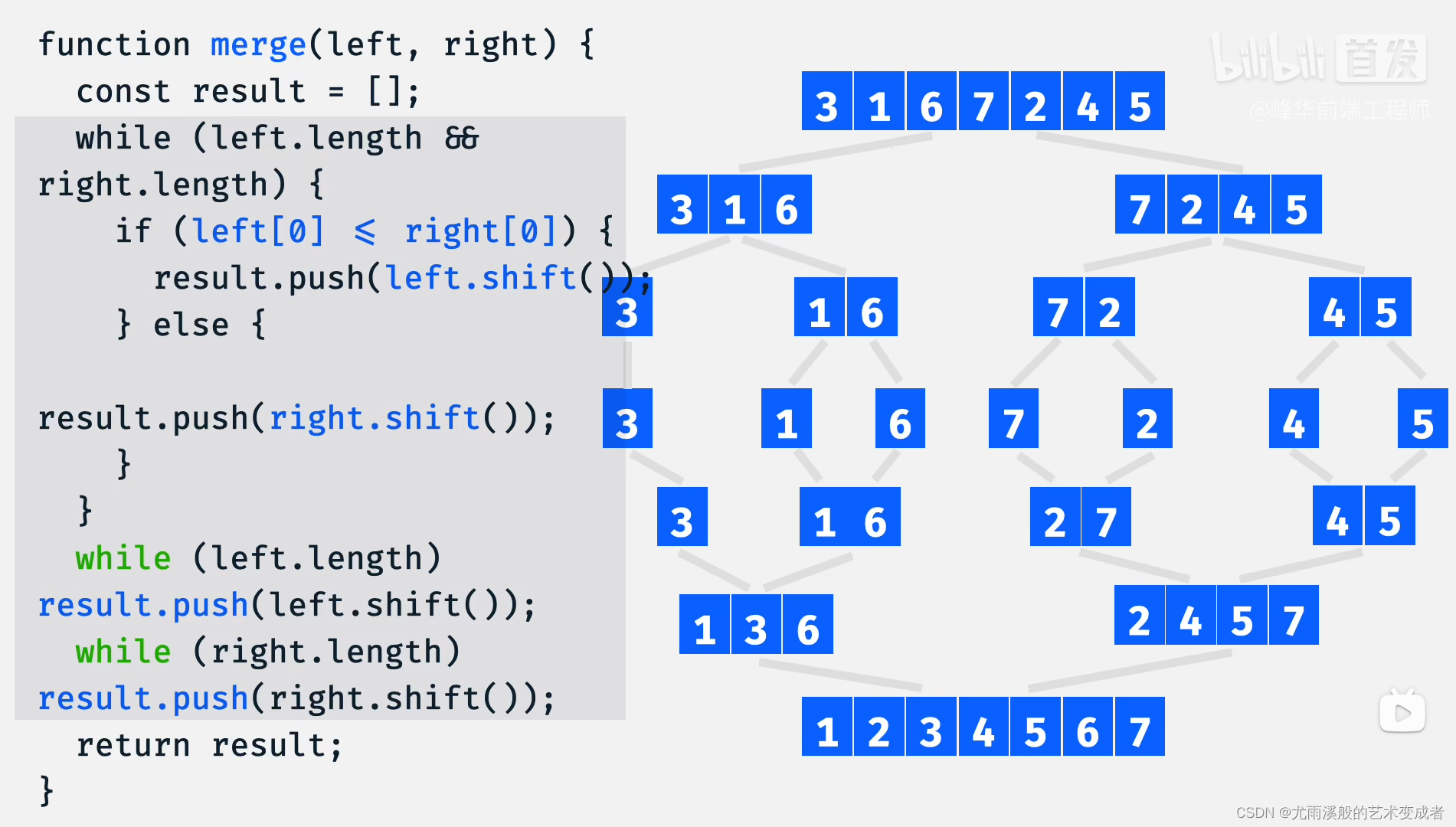
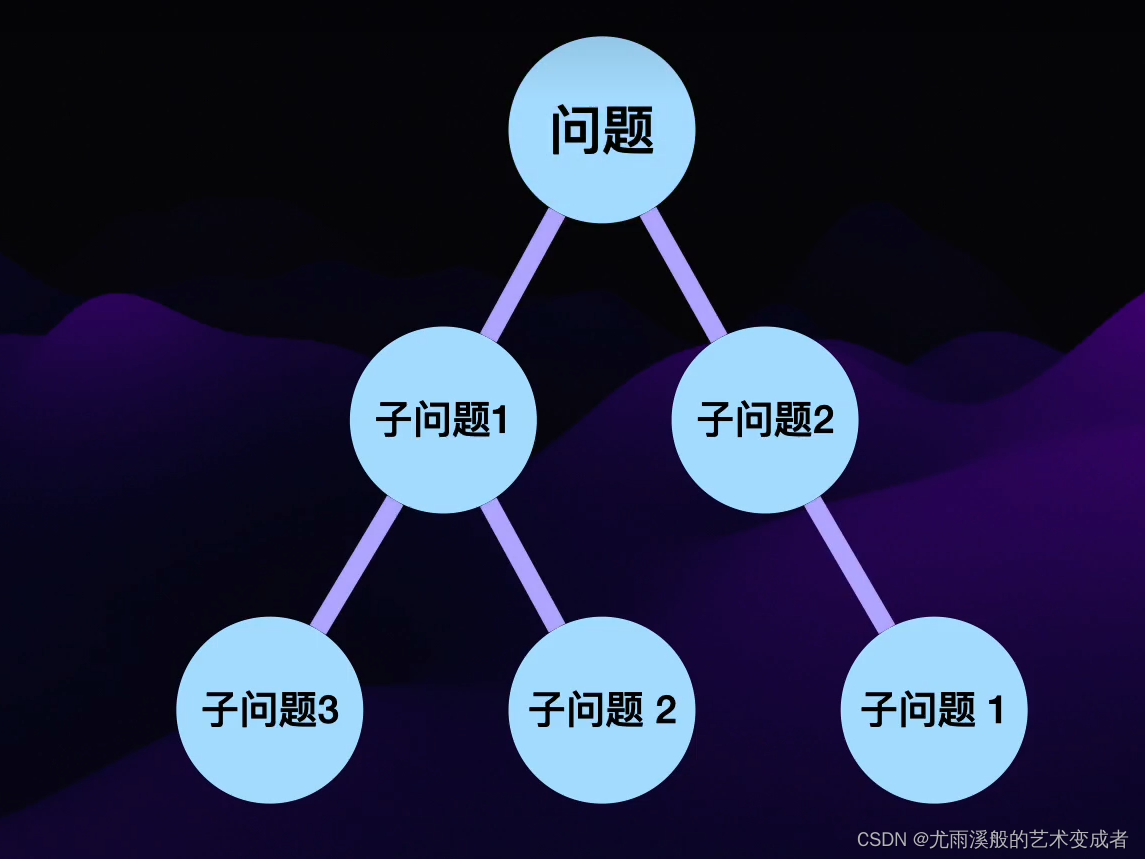
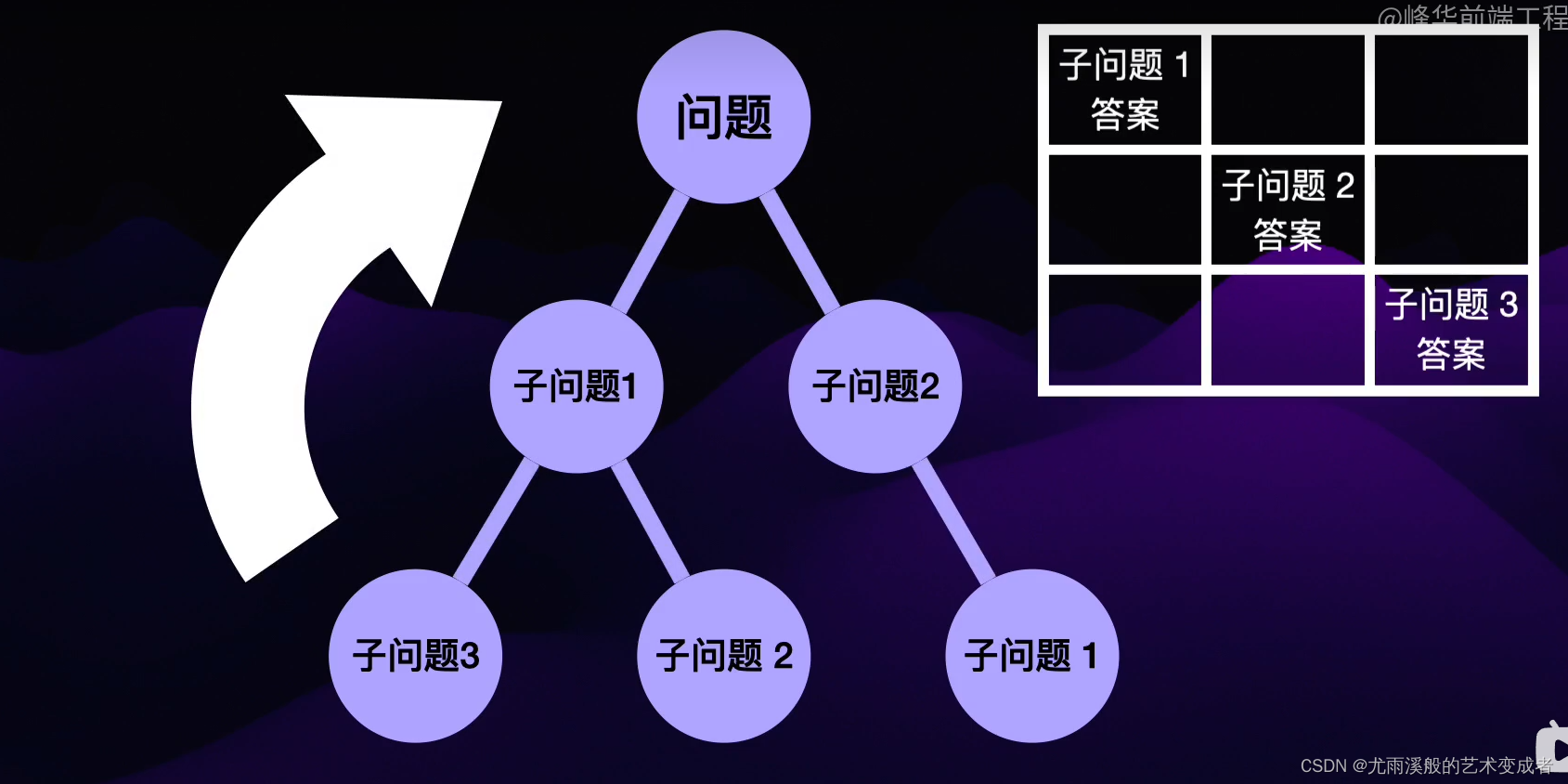
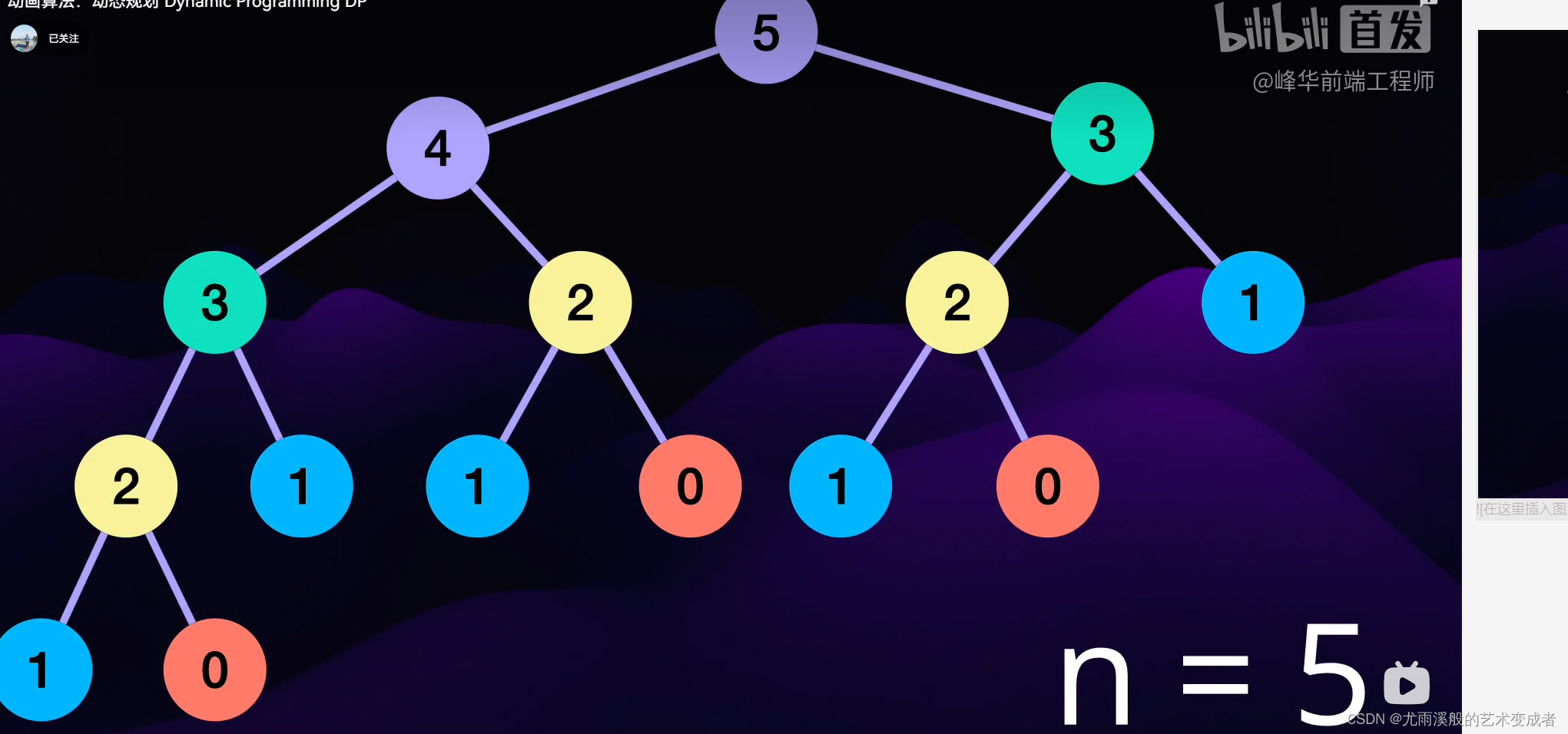
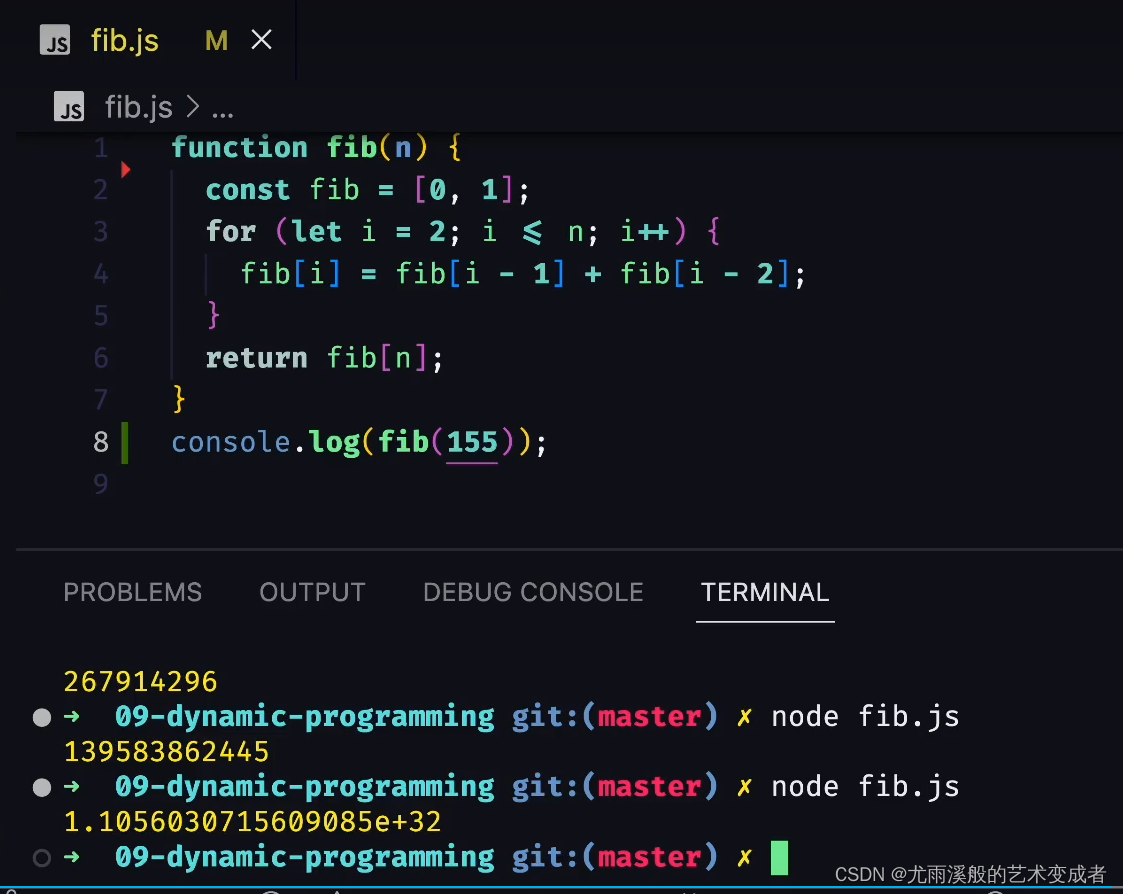
动态规划 Dynamic Programming DP










![[Linux]Linux编译器-gcc/g++](https://img-blog.csdnimg.cn/3c357f0f31a24e15a751951ce461f9db.png)