Cliff-Walking问题的描述

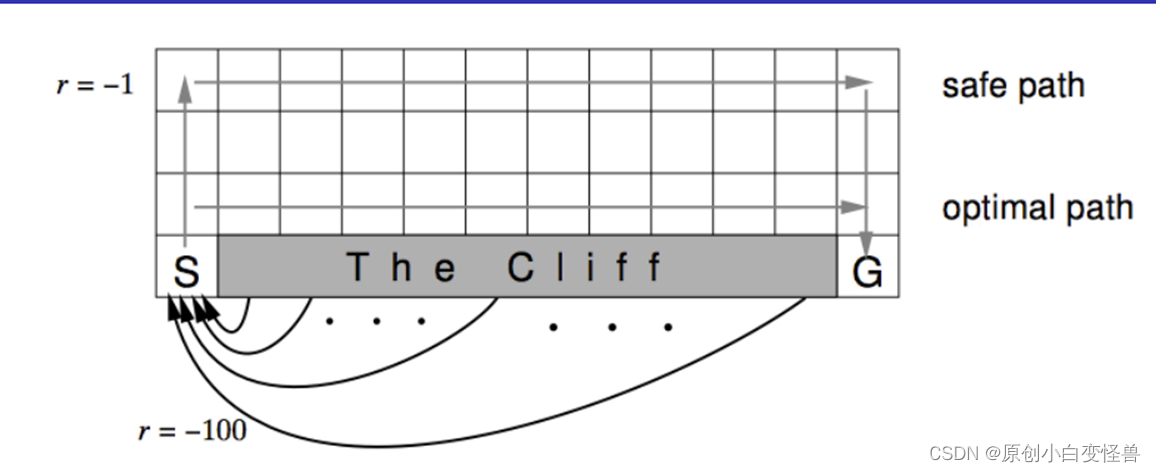
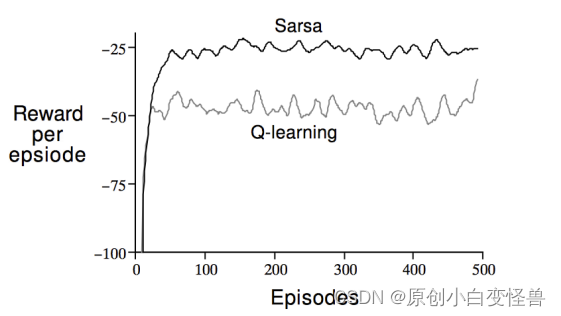
在这里插入图片描述

悬崖行走：从S走到G，其中灰色部分是悬崖不可到达，求可行方案
建模中，掉下悬崖的奖励是-100，G的奖励是10，原地不动的奖励-1，到达非终点位置的奖励是0(与图中的示意图不一致，不过大差不差)，分别使用同轨策略的Sarsa与离轨策略的Q-learning算法，经过20000幕进化迭代得出safe path，optimal path，最后根据Q值来得出最终的策略，以此来对上图进行复现

Sarsa和Q-Learning算法对比

Sarsa算法
在这里插入图片描述
Q-Learning算法

在这里插入图片描述首先要介绍的是什么是ε-greedy，即ε-贪心算法，一般取定ε为一个较小的0-1之间的值（比如0.2）
在算法进行的时候，用计算机产生一个伪随机数，当随机数小于ε时采取任意等概率选择的原则，大于ε时则取最优的动作。

在介绍完两个算法和ε-贪心算法之后，一言概之就是，Sarsa对于当前状态s的a的选择是ε-贪心的，对于s’的a‘的选择也是ε-贪心的Q-Learning与sarsa一样，只是对于s’的a‘的选择是直接取最大的。

代码分享

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches  # 图形类

np.random.seed(2022)


class Agent():
    terminal_state = np.arange(36, 48)  # 终止状态

    def __init__(self, board_rows, board_cols, actions_num, epsilon=0.2, gamma=0.9, alpha=0.1):
        self.board_rows = board_rows
        self.board_cols = board_cols
        self.states_num = board_rows * board_cols
        self.actions_num = actions_num
        self.epsilon = epsilon
        self.gamma = gamma
        self.alpha = alpha
        self.board = self.create_board()
        self.rewards = self.create_rewards()
        self.qtable = self.create_qtable()

    def create_board(self):  # 创建面板
        board = np.zeros((self.board_rows, self.board_cols))
        board[3][11] = 1
        board[3][1:11] = -1
        return board

    def create_rewards(self):  # 创建奖励表
        rewards = np.zeros((self.board_rows, self.board_cols))
        rewards[3][11] = 10
        rewards[3][1:11] = -100
        return rewards

    def create_qtable(self):  # 创建Q值
        qtable = np.zeros((self.states_num, self.actions_num))
        return qtable

    def change_axis_to_state(self, axis):  # 将坐标转化为状态
        return axis[0] * self.board_cols + axis[1]

    def change_state_to_axis(self, state):  # 将状态转化为坐标
        return state // self.board_cols, state % self.board_cols

    def choose_action(self, state):  # 选择动作并返回下一个状态
        if np.random.uniform(0, 1) <= self.epsilon:
            action = np.random.choice(self.actions_num)
        else:
            p = self.qtable[state, :]
            action = np.random.choice(np.where(p == p.max())[0])

        r, c = self.change_state_to_axis(state)
        new_r = r
        new_c = c

        flag = 0

        #状态未改变
        if action == 0:  # 上
            new_r = max(r - 1, 0)
            if new_r == r:
                flag = 1
        elif action == 1:  # 下
            new_r = min(r + 1, self.board_rows - 1)
            if new_r == r:
                flag = 1
        elif action == 2:  # 左
            new_c = max(c - 1, 0)
            if new_c == c:
                flag = 1
        elif action == 3:  # 右
            new_c = min(c + 1, self.board_cols - 1)
            if new_c == c:
                flag = 1

        r = new_r
        c = new_c
        if flag:
            reward = -1 + self.rewards[r,c]
        else:
            reward = self.rewards[r, c]

        next_state = self.change_axis_to_state((r, c))
        return action, next_state, reward


    def learn(self, s, r, a, s_,sarsa_or_q):
        # s状态，a动作，r即时奖励，s_演化的下一个动作
        q_old = self.qtable[s, a]
        # row,col = self.change_state_to_axis(s_)
        done = False
        if s_ in self.terminal_state:
            q_new = r
            done = True
        else:
            if sarsa_or_q == 0:
                if np.random.uniform(0.1) <= self.epsilon:
                    s_a = np.random.choice(self.actions_num)
                    q_new = r + self.gamma * self.qtable[s_, s_a]
                else:
                    q_new = r + self.gamma * max(self.qtable[s_, :])
            else:
                q_new = r + self.gamma * max(self.qtable[s_, :])
                # print(q_new)
        self.qtable[s, a] += self.alpha * (q_new - q_old)
        return done


    def initilize(self):
        start_pos = (3, 0)  # 从左下角出发
        self.cur_state = self.change_axis_to_state(start_pos)  # 当前状态
        return self.cur_state


    def show(self,sarsa_or_q):
        fig_size = (12, 8)
        fig, ax0 = plt.subplots(1, 1, figsize=fig_size)
        a_shift = [(0, 0.3), (0, -.4),(-.3, 0),(0.4, 0)]
        ax0.axis('off')  # 把横坐标关闭
        # 画网格线
        for i in range(self.board_cols + 1):  # 按列画线
            if i == 0 or i == self.board_cols:
                ax0.plot([i, i], [0, self.board_rows], color='black')
            else:
                ax0.plot([i, i], [0, self.board_rows], alpha=0.7,
                     color='grey', linestyle='dashed')

        for i in range(self.board_rows + 1):  # 按行画线
            if i == 0 or i == self.board_rows:
                ax0.plot([0, self.board_cols], [i, i], color='black')
            else:
                ax0.plot([0, self.board_cols], [i, i], alpha=0.7,
                         color='grey', linestyle='dashed')

        for i in range(self.board_rows):
            for j in range(self.board_cols):

                y = (self.board_rows - 1 - i)
                x = j

                if self.board[i, j] == -1:
                    rect = patches.Rectangle(
                        (x, y), 1, 1, edgecolor='none', facecolor='black', alpha=0.6)
                    ax0.add_patch(rect)
                elif self.board[i, j] == 1:
                    rect = patches.Rectangle(
                        (x, y), 1, 1, edgecolor='none', facecolor='red', alpha=0.6)
                    ax0.add_patch(rect)
                    ax0.text(x + 0.4, y + 0.5, "r = +10")

                else:
                    # qtable
                    s = self.change_axis_to_state((i, j))
                    qs = agent.qtable[s, :]
                    for a in range(len(qs)):
                        dx, dy = a_shift[a]
                        c = 'k'
                        q = qs[a]
                        if q > 0:
                            c = 'r'
                        elif q < 0:
                            c = 'g'
                        ax0.text(x + dx + 0.3, y + dy + 0.5,
                                 "{:.1f}".format(qs[a]), c=c)

        if sarsa_or_q == 0:
            ax0.set_title("Sarsa")
        else:
            ax0.set_title("Q-learning")
        if sarsa_or_q == 0:
            plt.savefig("Sarsa")
        else:
            plt.savefig("Q-Learning")
        plt.show(block=False)
        plt.pause(5)
        plt.close()

加上下面这一段，就可以使程序跑起来啦！

agent = Agent(4, 12, 4)
maxgen = 20000
gen = 1
sarsa_or_q = 0
while gen < maxgen:
    current_state = agent.initilize()
    while True:
        action, next_state, reward = agent.choose_action(current_state)
        done = agent.learn(current_state, reward, action, next_state,sarsa_or_q)
        current_state = next_state
        if done:
            break

    gen += 1

agent.show(sarsa_or_q)
print(agent.qtable)

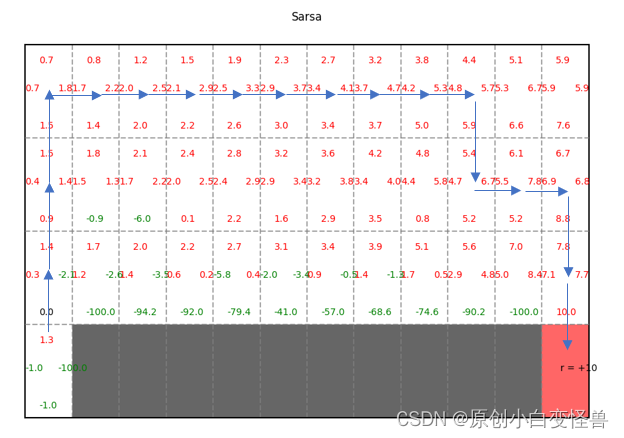
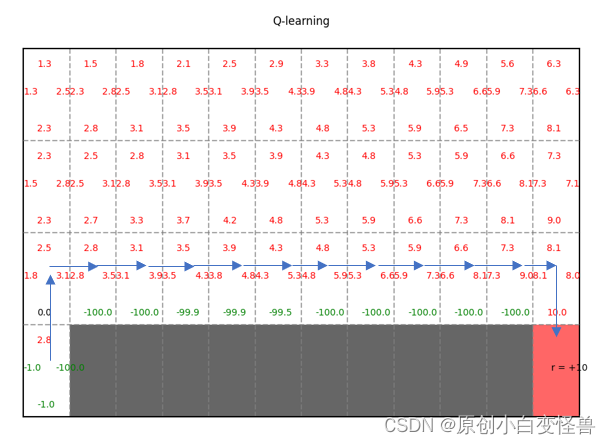
设置sarsa_or_q分别为0和1可以查看采用不同方法计算得的结果示意图
根据Q值就可以得到最后的收敛策略
在这里插入图片描述

需要改进的地方

代码迭代的收敛太慢，笔者写的代码迭代了20000才收敛，这与课程中的100幕左右就收敛的结果是不一致的，算法的效率上还需要改进。值得补充的是，100幕左右收敛在迭代最大代数中并没有做到，所以在模拟仿真的时候，索性就选择了20000次，说不定提前就收敛了。
可以改进的地方：对模型进行建立，因为之前代码是无模型的，设立模型对策略进行引导会得到更好的结果，当然也有可能使问题陷入局部探索之中，这是继续深入学习需要讨论的。
与科研科研结合的地方：在研究方向上，如果要结合的话，需要学习多个个体在环境下同时学习时的处理方法
在这里插入图片描述