动态规划具体指的是在某些复杂问题中,将问题转化为若干个子问题,并在求解每个子问题的过程中保存已经求解的结果,以便后续使用。实际上动态规划更像是一种通用的思路,而不是具体某个算法。
在强化学习中,被用于求解值函数和最优策略,如策略迭代、Q-learning算法。
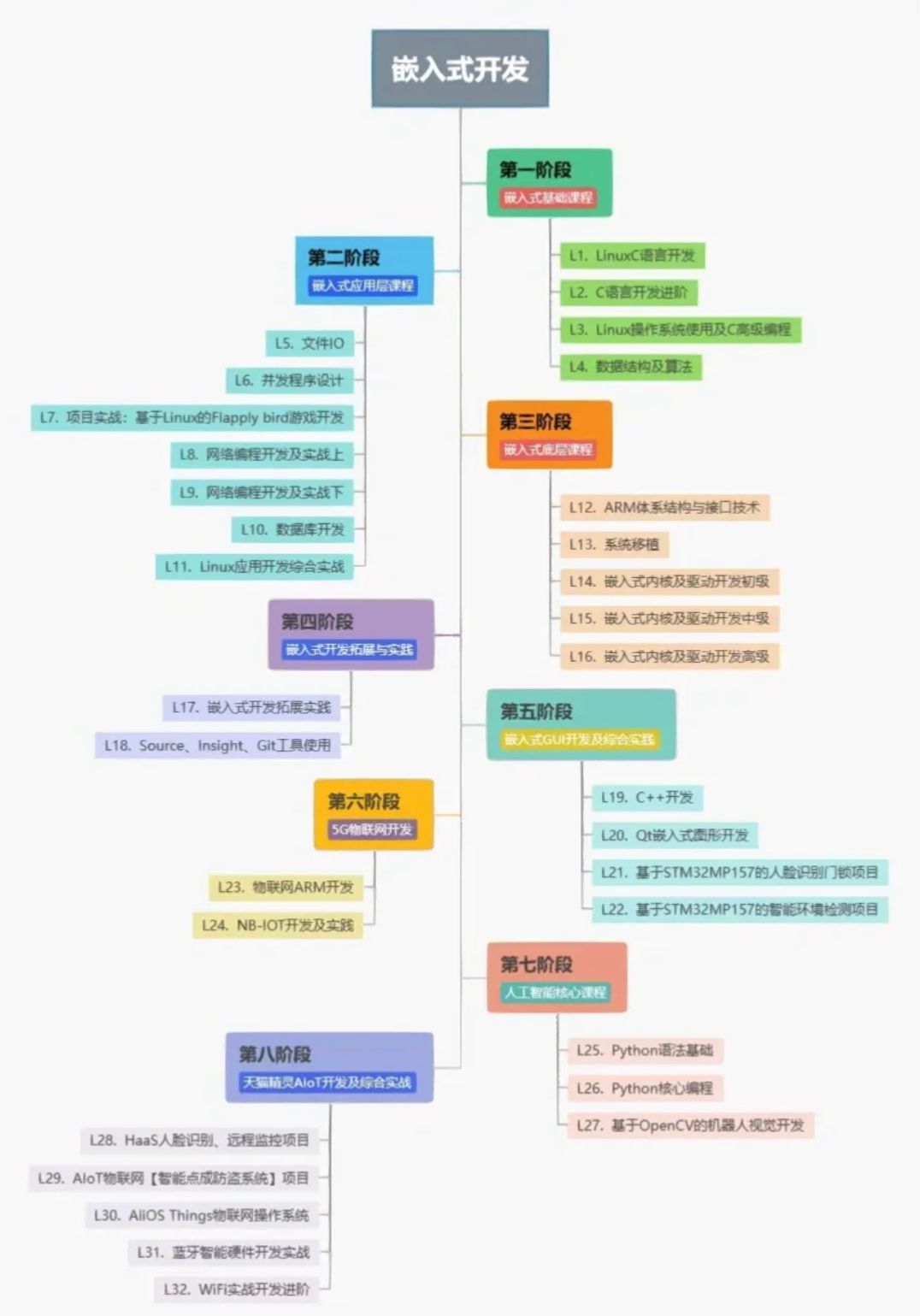
编程思想——以算法题举例

一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径?
为了到达横坐标为i,纵坐标为j点,我们定义
f
(
i
,
j
)
f(i,j)
f(i,j) 来表示从 (0,0) 到 (i,j) 点的所有路径。由于机器人只能向右或者向下走,所有 (i,j) 上一个点必定为 (i,j-1) 或 (i-1,j),那么
f
(
i
,
j
)
=
f
(
i
,
j
−
1
)
+
f
(
i
−
1
,
j
)
f(i,j)=f(i,j-1)+f(i-1,j)
f(i,j)=f(i,j−1)+f(i−1,j)
同时,机器人不能跑出边界,因此需要设置边界条件:
f
(
i
,
j
)
=
{
0
,
i
=
0
,
j
=
0
1
,
i
=
0
,
j
≠
0
1
,
i
≠
0
,
i
=
0
f
(
i
−
1
,
j
)
+
f
(
i
,
j
−
1
)
f(i,j)=\begin{cases}\begin{aligned}0,i&=0,j=0\\1,i&=0,j\neq0\\1,i&\neq0,i=0\\f(i-1,j)+f(i,j-1)\end{aligned}&\end{cases}
f(i,j)=⎩
⎨
⎧0,i1,i1,if(i−1,j)+f(i,j−1)=0,j=0=0,j=0=0,i=0

def solve(m,n):
# 初始化边界条件
f = [[1] * n] + [[1] + [0] * (n - 1) for _ in range(m - 1)]
# 状态转移
for i in range(1, m):
for j in range(1, n):
f[i][j] = f[i - 1][j] + f[i][j - 1]
return f[m - 1][n - 1]
动态规划问题有三个性质,最优化原理、无后效性和有重叠子问题,符合强化学习求得最大化累计回报的问题。