目录
前言
方法一
方法二
方法三
前言
题目链接:338. 比特位计数 - 力扣(LeetCode)
题目:
输入一个非负数 n,请计算 0 到 n 之间每个数字的二进制形式中 1 的个数,并输出一个数组。例如,输入的 n 为 4,由于 0、1、2、3、4 的二进制形式中 1 的个数分别为 0、1、1、2、1,因此输出数组 [0, 1, 1, 2, 1]。
分析:
很多人在面试的时候都能想到直观的解法,使用一个 for 循环来计算从 0 到 n 的每个整数 i 的二进制形式中 1 的个数。于是问题转换成如何求一个整数 i 的二进制形式中 1 的个数。
方法一
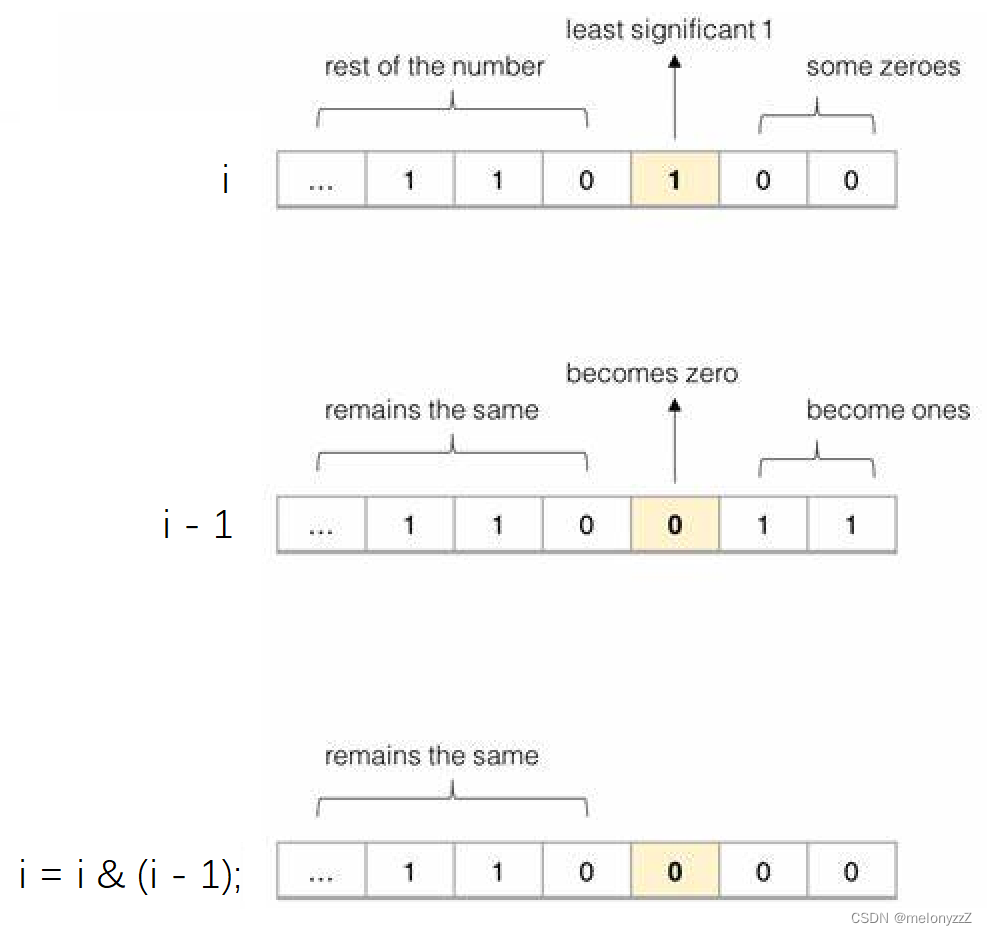
计算整数 i 的二进制形式中 1 的个数有多种不同的方法,其中一种比较高效的方法是每次使用 i = i & (i - 1); 将整数 i 的最右边的 1 变成 0。
整数 i 减去 1,那么它最右边的 1 变成 0,如果它的右边还有 0,则右边所有的 0 都变成 1,而其左边所有位都保存不变。因此,i = i & (i - 1); 相当于将整数 i 的最右边的 1 变成 0。
class Solution {
public:
vector<int> countBits(int n) {
vector<int> result(n + 1, 0);
for (int i = 0; i <= n; ++i)
{
int tmp = i;
while (tmp != 0)
{
++result[i];
tmp = tmp & (tmp - 1);
}
}
return result;
}
};如果一个整数共有 k 位,那么它的二进制形式中可能有 O(k) 个 1。在上述代码中,while 循环中的代码对每个整数将执行 O(k) 次,因此,上述代码的时间复杂度是 O(nk)。
方法二
根据前面的分析可知,i = i & (i - 1); 将 i 的二进制形式中最右边的 1 变成 0,也就是说,整数 i 的二进制形式中 1 的个数比整数 i & (i - 1) 的二进制中 1 的个数多 1。
class Solution {
public:
vector<int> countBits(int n) {
vector<int> result(n + 1, 0);
for (int i = 1; i <= n; ++i) // 注意:i 从 1 开始
{
result[i] = result[i & (i - 1)] + 1;
}
return result;
}
};不管整数 i 的二进制形式中有多少个 1,上述代码只根据 O(1) 的时间就能得出整数 i 的二进制形式中 1 的数目,因此时间复杂度位 O(n)。
方法三
还可以使用另一种思路来解决这个问题。
如果正整数 i 是一个偶数,即最低位为 0,那么 i 的二进制形式中 1 的个数和 "i >> 1" 是相同的。
如果正整数 i 是一个奇数,即最低位为 1,那么 i 的二进制形式中 1 的个数比 "i >> 1" 多 1。
class Solution {
public:
vector<int> countBits(int n) {
vector<int> result(n + 1, 0);
for (int i = 1; i <= n; ++i) // 注意:i 从 1 开始
{
result[i] = result[i >> 1] + (i & 1);
}
return result;
}
};上述代码用 "i & 1" 计算 "i % 2",这是因为位运算比求余运算更高效。
这种解法的时间复杂度也是 O(n)。