一、介绍
在统计建模和机器学习领域,回归分析是用于理解变量之间关系的基本工具。在各种类型的回归技术中,岭回归是一种特别有用的方法,尤其是在处理多重共线性和过拟合时。本文深入探讨了岭回归的概念、其数学基础、应用、优点和局限性。
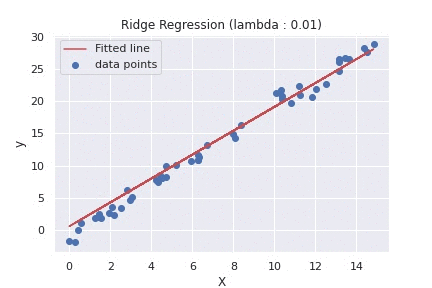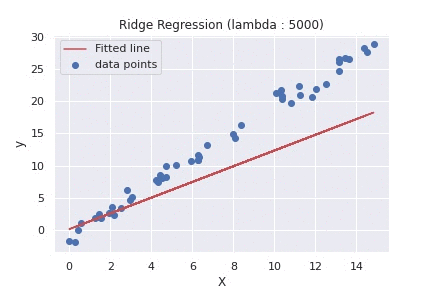
在数据领域,就像在生活中一样,阻力最小的路径往往会导致道路人满为患。Ridge Regression 就像一个明智的指南,将我们带到一条人迹罕至的路线上,那里的旅程可能稍微复杂一些,但到达目的地的准确性和可靠性更高。
二、背景
岭回归,也称为 Tikhonov 正则化,是一种用于分析多重共线性的多元回归数据的技术。当回归模型中的自变量高度相关时,就会发生多重共线性。这种情况可能导致普通最小二乘法 (OLS) 回归中回归系数的估计值不可靠且不稳定。Ridge Regression 通过在回归模型中引入惩罚项来解决此问题。
三、数学基础
岭回归背后的基本思想是在回归模型中系数的平方和中添加一个惩罚(岭惩罚)。岭惩罚是系数大小乘以称为 lambda (λ) 的参数的平方,该参数控制惩罚的强度。
岭回归模型表示为:
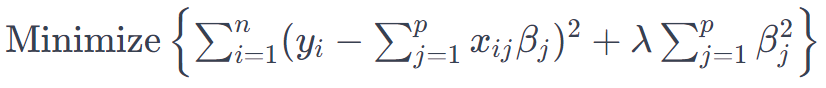
其中 yi 是因变量,xij 是自变量,βj 是系数,n 和 p 分别表示观测值和预测变量的数量。
四、应用与优势
岭回归广泛用于 OLS 回归无法提供可靠估计的情况:
- 处理多重共线性:通过对系数进行惩罚,岭回归减少了多重共线性问题,从而获得更可靠的估计。
- 防止过拟合:该技术可用于防止模型中的过拟合,尤其是在预测变量数量相对于观测值数量较大的情况下。
- 提高预测准确性:由于偏差-方差权衡,岭回归可以提高预测准确性。
五、局限性
尽管有其优点,但岭回归也有局限性:
- Lambda 的选择:为 lambda 参数选择适当的值至关重要。通常使用交叉验证,但它可能是计算密集型的。
- 偏置估计器:该方法在回归系数的估计中引入了偏置。但是,这是为了降低方差和提高预测准确性而进行的权衡。
- 功能选择的不适用性:Ridge Regression 不执行特征选择;它只是将系数缩小到零,但永远不会完全缩小到零。
六、代码
为了演示 Python 中的 Ridge 回归,我们将遵循以下步骤:
- 创建合成数据集。
- 将数据集拆分为训练集和测试集。
- 将 Ridge 回归应用于数据集。
- 评估模型的性能。
- 绘制结果。
下面是一个完整的 Python 代码示例来说明此过程:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_regression
# Step 1: Create a synthetic dataset
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)
# Step 2: Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Step 3: Apply Ridge Regression to the dataset
# Note: Adjust alpha to see different results (alpha is the λ in Ridge formula)
ridge_model = Ridge(alpha=1.0)
ridge_model.fit(X_train, y_train)
# Predictions
y_train_pred = ridge_model.predict(X_train)
y_test_pred = ridge_model.predict(X_test)
# Step 4: Evaluate the model's performance
train_error = mean_squared_error(y_train, y_train_pred)
test_error = mean_squared_error(y_test, y_test_pred)
print(f"Train MSE: {train_error}, Test MSE: {test_error}")
# Step 5: Plot the results
plt.scatter(X_train, y_train, color='blue', label='Training data')
plt.scatter(X_test, y_test, color='red', label='Testing data')
plt.plot(X_train, y_train_pred, color='green', label='Ridge model')
plt.title("Ridge Regression with Synthetic Dataset")
plt.xlabel("Feature")
plt.ylabel("Target")
plt.legend()
plt.show()Train MSE: 73.28536502082304, Test MSE: 105.78604284136125若要运行此代码,请执行以下操作:
- 确保安装了 Python 和必要的库:NumPy、Matplotlib 和 scikit-learn。
- 您可以在 Ridge 函数中调整参数,以查看不同值如何影响模型。代码中的参数对应于 Ridge 回归公式中的 λ (lambda)。
alphaalpha - 合成数据集是使用 scikit-learn 的函数生成的,该函数创建适合回归的数据集。
make_regression

此代码将创建一个 Ridge 回归模型,将其应用于合成数据集,使用均方误差 (MSE) 评估其性能,并显示一个图,显示 Ridge 回归模型与训练和测试数据的拟合。
结论
岭回归是一种强大的统计工具,用于处理回归分析中的一些固有问题,例如多重共线性和过拟合。通过合并惩罚项,它为普通最小二乘回归提供了一种强大的替代方案,尤其是在具有许多预测变量的复杂数据集中。虽然它给模型带来了一些偏差,但这通常是值得的,以换取稳定性和预测准确性的提高。但是,从业者必须注意其局限性,包括选择适当的 lambda 值的挑战以及无法执行特征选择。总体而言,岭回归是统计学家、数据分析师和机器学习从业者武器库中不可或缺的技术。