🧑个人简介：大家好，我是尘觉，希望我的文章可以帮助到大家，您的满意是我的动力😉

在csdn获奖荣誉: 🏆csdn城市之星2名
⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　💓csdn2023年后端赛道第第七
⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　💓csdn2023年长沙赛道第一
⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　💓csdn2023年大二赛道第二
⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　💓Java全栈群星计划top前5
⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　🤗 端午大礼包获得者
⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　🥰阿里云专家博主
⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　⁣⁣⁣⁣　😉亚马逊DyamoDB结营
获得国家荣誉3项省级荣誉4项以及多项校院级

💕欢迎大家：这里是CSDN，我总结知识的地方，欢迎来到我的博客，感谢大家的观看🥰
如果文章有什么需要改进的地方还请大佬不吝赐教 先在次感谢啦😊

数据结构——初识线性表

介绍

​ 在一列火车中，每个车厢都有一个特定的位置，车厢按照一个明确的顺序相连。这类似于线性表中的元素按照特定的顺序排列。每个车厢都知道它前面和后面连接的车厢是哪一个（就像线性表中的每个元素都有一个前驱和一个后继）。

​ 在这样的结构中，可以很容易地添加或删除车厢（在线性表中这对应于插入和删除操作）。例如，如果我们想在第3车厢和第4车厢之间添加一个新的车厢，我们可以断开第3车厢和第4车厢之间的连接，然后将新的车厢插入其中。

​ 同时，如果我们知道第5车厢后面是什么车厢，我们可以非常快速地找到它（这对应于线性表中的访问操作）。

​ 此外，车长可以通过检查每个车厢来确保所有的车厢都处于正确的位置，并且没有车厢被遗漏。如果一个车厢丢失了，那么这将很快被发现，因为它前后的车厢将不再连接。

线性表的定义

由n(n≥O)个数据特性相同的元素构成的有限序列称为线性表。

• 线性表中元素的个数n(n≥O)定义为线性表的长度，n=O时称为空表。
• 将非空的线性表(n>O)记作(a1，a2，a3，…，an)
• 这里的数据元素ai(1≤i≤n)只是个抽象的符号，其具体含义在不同情况下可以不同。
• 在非空的线性表，有且仅有一个开始结点a1,它没有直接前趋，而仅有一个直接后继a2;
• 有且仅有一个终端结点an,它没有直接后继，而仅有一个直接前趋an-1;
• 其余的内部结点ai,(2<i<n-1)都有且仅有一个直接前趋ai-1和一个直接后继ai+1

解读

线性表就像是一个排队的队列。队列的长度可以用来描述里面有多少人正在排队，我们把这个称作“线性表的长度”。如果队列里没有人，我们就说这个队列是“空的”。

在一个非空的队列里，我们可以用一个列表来表示所有在队列中的人：(a1, a2, a3, …, an)。

在这里：

• “a1”是第一个人，在队列的最前面。他前面没有人。
• “an”是最后一个人，在队列的最后。他后面没有人。
• 中间的每个人，比如“a2”到“an-1”，都有一个人在他前面和一个人在他后面。

这样，每个人都知道他前后是谁，从而形成了一个有序的队列。

线性表的例子

26个英文字母的字母表：(A, B, C, …，Z)；学生信息表；12星座。

同一线性表中的元素必定具有相同的特性，数据元素之间关系是线性的。

案例引入

逻辑结构抽象为线性表存储结构呢？

运行的多项式时，就要用一个长度为20001的线性表来表示，而表中仅有3个非零元素，此时将会造成存储空间的很大浪费，由此可改变元素设定，对多项式的每一项，可用（系数，指数）唯一确定。

每一个系数与指数也构成了一个线性表只不过是线性表的每个数据元素有2个数据项

用结构体数组存储，(结构体实现每一项。)这个我们以后会相信的说的。

多项式操作

• 加法

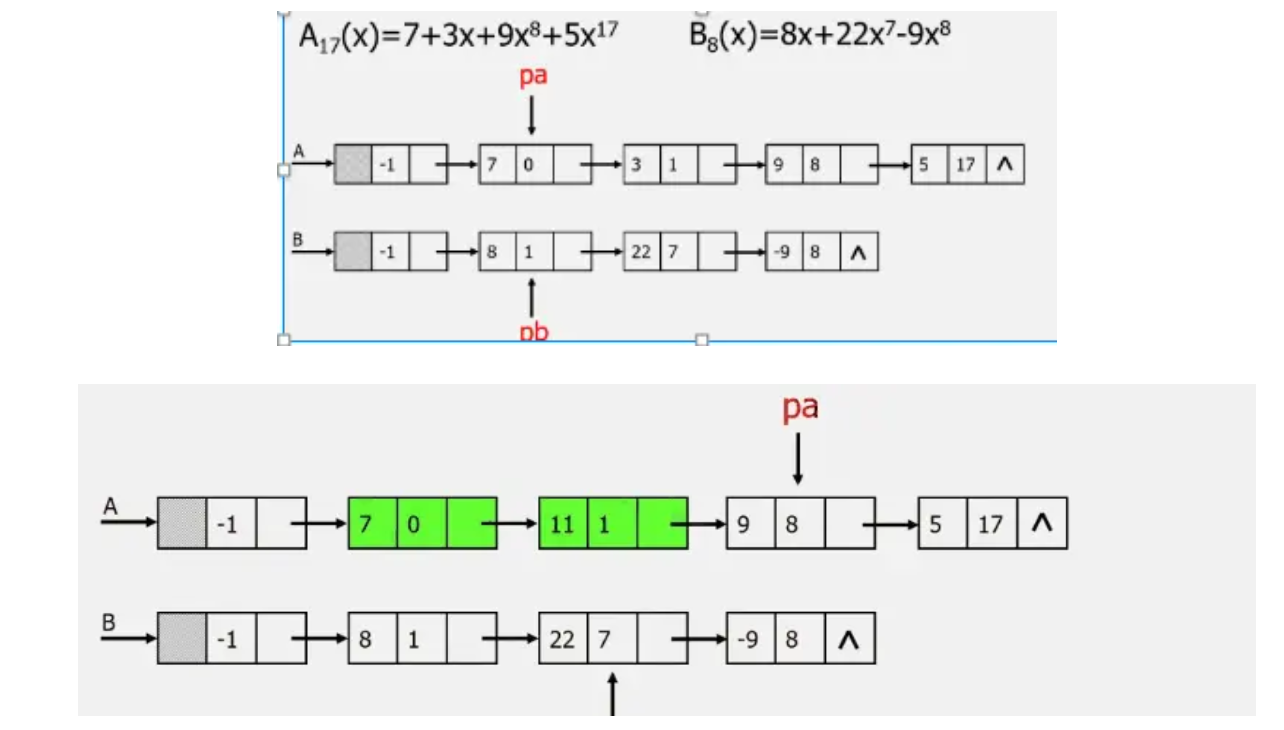
A=((7,0),(3,1),(9,8),(5,17))[4项]

B=((8,1),(22,7),(-9,8),)[3项]

创建一个新的多项式c用来存放a与b和分别从头遍历比较a和b的每一项指数相同，对应系数相加，若其和不为零，则在c中增加一个新项指数不相同，则将指数较小的项复制到c中一个多项式已遍历完毕时，将另一个剩余项依次复制到c中即可

和有多少项呢？

最少:指数一样,系数正好互为相反数项数为0最多指数都不一样项数为元素个数之和。项数不容易确定太大了浪费空间，太小了放不下。顺序存储结构存在问题存储空间分配不灵活；运算的空间复杂度高尝试链式存储结构(不需要额外的空间只利用已有的空间)

案例:

​ 图书信息管理系统。出版社有一些图书数据保存在一个文本文件 book.txt中,为简单起见,在此假设每种图书只包括三部分信息:SBN(书号)、书名和价格,文件中的部分数据如图所示。现要求实现一个图书信息管理系统,包括以下6个具体功能。

• (1)查找:根据指定的ISBN或书名查找相应图书的有关信息,并返回该图书在表中的位置序号。
• (2)插入:插入一种新的图书信息。
• (3)删除:删除一种图书信息。
• (4)修改:根据指定的ISBN,修改该图书的价格
• (5)排序:将图书按照价格由低到高进行排序。
• (6)计数:统计图书表中的图书数量。

逻辑结构：根据图书表的特点将其抽象成一个线性表，每本图书作为线性表中的一个元素

存储结构：

a.顺序

b.链式

😁热门专栏推荐
想学习vue的可以看看这个

java基础合集

数据库合集

redis合集

nginx合集

linux合集

手写机制

微服务组件

spring_尘觉

springMVC

mybits

等等等还有许多优秀的合集在主页等着大家的光顾感谢大家的支持

🤔欢迎大家加入我的社区 尘觉社区

文章到这里就结束了，如果有什么疑问的地方请指出，诸佬们一起来评论区一起讨论😁
希望能和诸佬们一起努力，今后我们一起观看感谢您的阅读🍻
如果帮助到您不妨3连支持一下，创造不易您们的支持是我的动力🤞