一、说明

致谢:AI 代理简介:Auto-GPT、AgentGPT 和 BabyAGI 入门 | 数据营
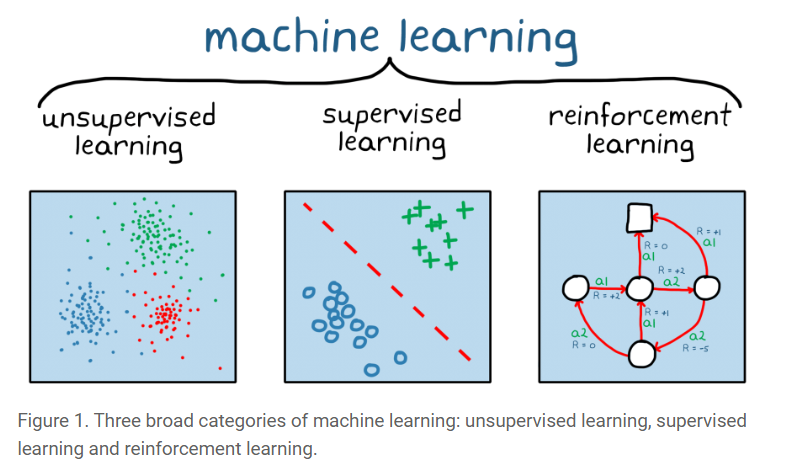
二、什么是强化学习?
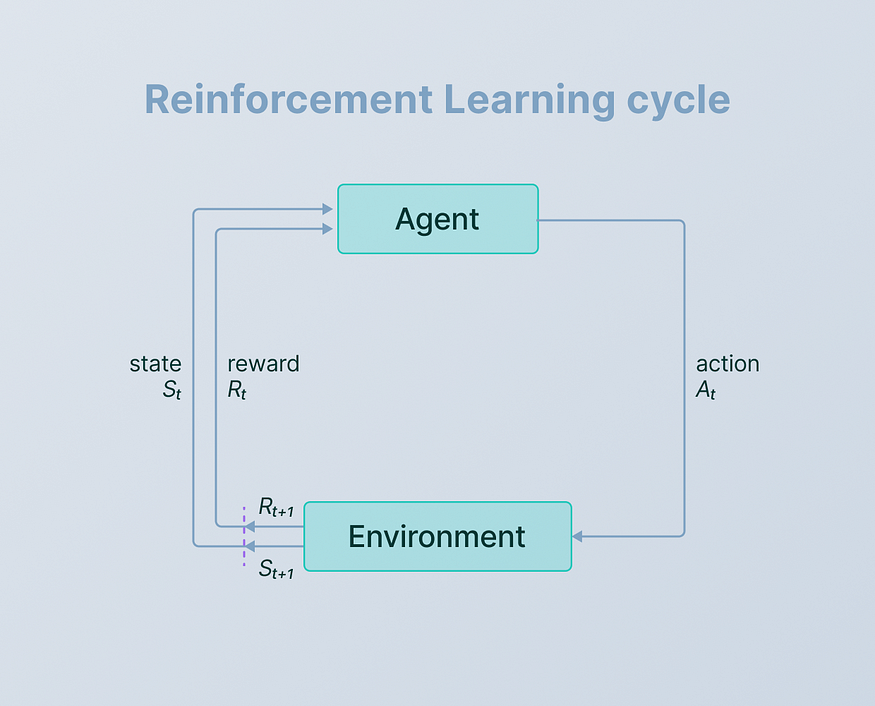
强化学习(RL)是一种机器学习范例,其中代理通过与环境交互来学习。代理做出决策并以奖励或惩罚的形式接收反馈,使其能够随着时间的推移学习最佳策略。与依赖于标记示例的监督学习和侧重于发现模式的无监督学习不同,强化学习以从动态交互中学习为中心,通过顺序决策来最大化累积奖励。
学分:什么是强化学习?— MATLAB 和 Simulink (mathworks.com)
强化学习问题中需要了解的术语很少:
- 代理- 代理是在环境中做出决策并采取行动的实体。它可以是机器人、游戏角色或任何能够学习并与周围环境交互的系统。
- 环境——环境是代理运行的外部设置或场景。它包括代理之外可以影响代理行为或受代理行为影响的所有内容。例如,在游戏中,环境包括虚拟世界、障碍物和其他游戏元素。
- 动作——动作是代理在环境中做出的移动或决定。它可以是选择移动方向、选择策略或影响智能体状态并进而影响环境的任何其他决策。
- 状态 -状态代表环境的当前情况或条件。这是代理用来决定下一步采取什么操作的信息。在游戏中,状态可以包括代理的位置、健康状况以及其他角色的位置。
- 奖励——奖励是代理在采取行动后从环境中收到的反馈。它们表示行动的直接利益或后果。积极的奖励鼓励代理人重复某些行为,而消极的奖励则阻止不良行为。在游戏中,奖励可以是完成关卡时获得的积分,也可以是碰撞障碍物时损失的积分。
三、马尔可夫决策过程
在数学上,马尔可夫决策过程(MDP)是一个离散时间随机控制过程。它提供了一个数学框架,用于在结果部分随机,部分受决策者控制的情况下建模决策。MDP对于研究通过动态规划解决的优化问题非常有用。MDP至少早在20世纪50年代就为人所知;关于马尔可夫决策过程的核心研究来源于罗纳德·霍华德(Ronald Howard)1960年的著作《动态规划与马尔可夫过程》。 它们被用于许多学科,包括机器人学、自动控制、经济学和制造业。MDP的名字来自俄罗斯数学家安德烈·马尔科夫,因为它们是马尔科夫链的延伸。
马尔可夫决策过程(MDP)是人工智能和决策理论中使用的数学框架。它提供了一种结构化的方法来对代理与环境交互的决策过程进行建模。中心思想是系统的未来状态仅取决于其当前状态和所采取的行动,表现出马尔可夫特性。MDP 涉及定义状态、动作、转换、奖励和策略,目的是为代理找到最佳策略,以随着时间的推移最大化累积奖励。
为了理解 MDP,我们以一个处于以下阶段之一的机器人为例:
坐着、站着、脚向前、摔倒、关机和举手
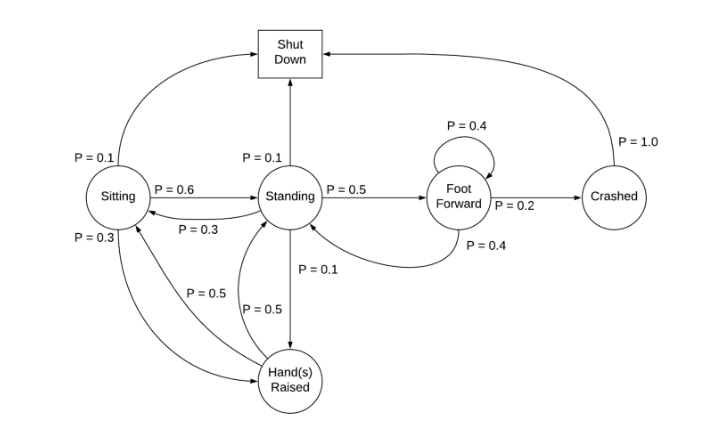
机器人的马尔可夫决策过程
如果我们看到上图,从一种状态转换到另一种状态的概率称为状态转换概率。
有关马尔可夫决策过程、转移矩阵和马尔可夫奖励过程的更多信息将在本系列的下一篇文章中介绍!