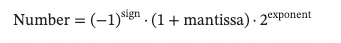计算机基础知识——数据的表示概述

news2024/11/17 9:39:04

1 进制转换

1.1 二进制、十进制和十六进制等常用数制及其相互转换

1.2 十进制和二进制之间转换

1.3 二进制数与八进制数、十六进制数之间的转换

2 码值：原码、反码、补码

2.1 原码

2.2 反码

2.3 补码

3 浮点数表示

3.1 浮点数的运算

1 进制转换

1.1 二进制、十进制和十六进制等常用数制及其相互转换

R进制，通常说法就是逢R进1.可以用的数为R个，分别是0,1,2,…，R–1.例如十进制数的基数为
10,即可以用到的数码个数为10,它们是0,1,2,3,4,5,6,7,8,9.二进制数的基数为2,可用的数码个数为2,它们是0和1。

BCD码：十进制的二进制表示，

0：0000 1：0001 2：0010 3：0011 4：0100 5：0101

6：0110 7：0111 8：1000 9：1001

十进制的202可以表示成BCD码为0010 0000 0010；

十六进制表示法是用16个数字组成的，每4位二进制数字表示一位十六进制数，十六进制的数字表示从0-9,A,B,C,D,E,F共十六个字符。十六进制与二进制相互转换就是一位十六进制字符与四位二进制数字的相互转换过程。

1.2 十进制和二进制之间转换

十进制向二进制转换分两步进行:首先把该数的整数部分和小数部分转换为二进制数；然后再把这两部分合并起来即可。公式如下：

$N=(R_{n}R_{n-1}...R_{1}R_{0}R_{-1}...R_{-m}) =R_{n}*2^{n}+R_{n-1}*2^{n-1}+...+R_{1}*2+R_{0}+R_{-1}*2^{-1}+...+R_{-m}*2^{-m}$

例如二进制数10100.01的值可计算如下：

$10100.01=1*2^{4}+1*2^{2}+1*2^{-2}$

十进制向二进制转换，最常用的是“除以R取余法”。当R=2，就是二进制。例如将十进制94转换成二进制数。

将所得的余数从低位到高位排列（1011110）2就是94的二进制数。

1.3 二进制数与八进制数、十六进制数之间的转换

将二进制数转换为八进制数，只有将每3个二进制数转换为八进制数即可，将二进制数转换为十
六进制数，只要将每4个二进制数转换为八进制数即可。将八进制数转换为二进制数，只要将每个八进制数转换为3位二进制数即可，将十六进制数转换为二进制数，只要将每个十六进制数转换为4位二进制数即可。上面的转换都是以小数点作为计算数码个数的起点。八进制数和十六进制数转换可先转换为二进制数，然后再转换为目标进制。

2 码值：原码、反码、补码

2.1 原码

将最高位用做符号位（0表示正数，1表示负数），其余各位代表数值本身的绝对值的表示形
式。这种方式是最容易理解的。
例如，+11的原码是00001011,–11 的原码是10001011。
但是直接使用原码在计算时却会有麻烦，比如（1）+（–1） = 0,如果直接使用原码则：
(00000001)B + (1000001)B = (10000010)B
这样计算的结果是–2(十进制)，也就是说，使用原码直接参与计算可能会出现错误的结果。所以，原码的符号位不能直接参与计算，必须和其他位分开，这样会增加硬件的开销和复杂性。

2.2 反码

正数的反码与原码相同。负数的反码符号位为1,其余各位为该数绝对值的原码按位取反。这个取反的过程使得这种编码称为"反码"。
例如，–11的反码：11110100
同样对上面的加法，使用反码的结果是：
(00000001)B + (11111110)B = (11111111)B
这样的结果是负0，而在人们普遍的观念中，0是不分正负的。反码的符号位可以直接参与计算，
而且减法也可以转换为加法计算。

2.3 补码

正数的补码与原码相同。负数的补码是该数的反码加1,这个加1就是"补"。
例如，–11的补码：11110100+1 = 11110101
再次做加法是这样的：
(00000001)B + (11111111)B = (00000000)B
直接使用补码进行计算的结果是正确的。注意到我们这里只是举例，并非证明。
对一个补码表示的数，要计算其原码，只要对它再次求补，可得该数的原码。
由于补码能使符号位与有效值部分一起参加运算，从而简化运算规则，同时它也使减法运算转
换为加法运算，进一步简化计算机中运算器的电路，这使得在大部分计算机系统中，数据都使用补
码表示。

3 浮点数表示

定点数和浮动数的区别在于如何对待小数点，在运算方式上也不相同，衡量一个计算机系统，定点运算和浮点运算是两个重要的指标。定点数的小数点是隐含的，固定在某个位置。如果该位置是在数的最低位之后，就是定点整数。定点数表示比较简单，运算规则也比较容易实现，但是当数值范围变化大时，使用定点数表示和运算就比较困难。
为了表示更大范围的数值，可以使用浮点数表示法。
在表示一个很大的数时，我们常常使用一种称为科学计数法的方式：
$N=M*R^{e}$
其中M称为尾数，e是指数，R为基数。
浮点数就是使用这种方法来表示大范围的数，其中指数一般是2,8,16.而且对于特定机器而言，指数是固定不变的，所以在浮点数中指数并不出现。从这个表达式可以看出：浮点数表示的精读取决于尾数的宽度，范围取决于基数的大小和指数的宽度。

3.1 浮点数的运算

浮动数运算过程比定点数复杂，包括以下过程：
1）对阶
首先计算两个数的指数差，把指数小的向指数大的对齐，并将尾数右移指数差的位数，这样两个浮点数就完成了对阶的操作。可以看出，对阶的过程可能使得指数小的浮点数失去一些有效位。
如果两个浮点数阶数相差很大，大于指数小的浮点数的尾数宽度，那么对阶后那个浮点数的尾数就
变成了0,即当做机器零处理了。
2）尾数计算
对阶完成后，两个浮点数尾数就如同定点数，计算过程同定点数计算。
3）结果格式化
尾数计算后，可能会产生溢出，此时将尾数右移，同时指数加1,如果指数加1后发生了溢出，则
表示两个浮点数的运算发生了溢出。
如果尾数计算没有溢出，则尾数不断左移，同时指数减1,直到尾数为格式化数。如果这个过程
中，指数小于机器能表达的最小数，则将结果置"机器零",这种情况称为下溢。