文章目录
- 一、题目
- [NOIP2013 普及组] 车站分级
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 样例 #2
- 样例输入 #2
- 样例输出 #2
- 提示
- 二、题解
- 基本思路:
- 代码
一、题目
[NOIP2013 普及组] 车站分级
题目背景
NOIP2013 普及组 T4
题目描述
一条单向的铁路线上,依次有编号为
1
,
2
,
…
,
n
1, 2, …, n
1,2,…,n 的 $n $ 个火车站。每个火车站都有一个级别,最低为
1
1
1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。
注意:起始站和终点站自然也算作事先已知需要停靠的站点。
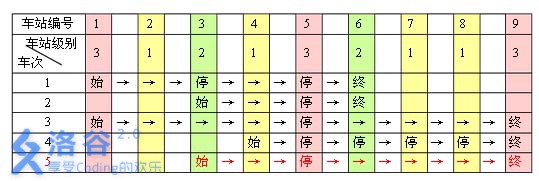
例如,下表是 5 趟车次的运行情况。其中,前 4 趟车次均满足要求,而第 5 5 5 趟车次由于停靠了 3 3 3 号火车站( 2 2 2 级)却未停靠途经的 6 6 6 号火车站(亦为 2 2 2 级)而不满足要求。
现有 m m m 趟车次的运行情况(全部满足要求),试推算这 $ n$ 个火车站至少分为几个不同的级别。
输入格式
第一行包含 2 2 2 个正整数 n , m n, m n,m,用一个空格隔开。
第 i + 1 i + 1 i+1 行 ( 1 ≤ i ≤ m ) (1 ≤ i ≤ m) (1≤i≤m) 中,首先是一个正整数 s i ( 2 ≤ s i ≤ n ) s_i\ (2 ≤ s_i ≤ n) si (2≤si≤n),表示第 $ i$ 趟车次有 s i s_i si 个停靠站;接下来有 $ s_i$ 个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式
一个正整数,即 n n n 个火车站最少划分的级别数。
样例 #1
样例输入 #1
9 2
4 1 3 5 6
3 3 5 6
样例输出 #1
2
样例 #2
样例输入 #2
9 3
4 1 3 5 6
3 3 5 6
3 1 5 9
样例输出 #2
3
提示
对于 $ 20%$ 的数据, 1 ≤ n , m ≤ 10 1 ≤ n, m ≤ 10 1≤n,m≤10;
对于 50 % 50\% 50% 的数据, 1 ≤ n , m ≤ 100 1 ≤ n, m ≤ 100 1≤n,m≤100;
对于 100 % 100\% 100% 的数据, 1 ≤ n , m ≤ 1000 1 ≤ n, m ≤ 1000 1≤n,m≤1000。
二、题解
基本思路:
- 题目让求n 个火车站最少划分的级别数。如果火车停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。
- 也就是说不是停靠站的火车站级别必须是比停靠站的级别小的,这就给出了点与点之间的关系。建图完毕后,拓扑排序中取级别较大的即可
代码
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define endl "\n"
#define int long long
#define fi first
#define se second
#define repn(i,o,n) for(int i=o;i<=n;i++)
#define rep(i,o,n) for(int i=o;i<n;i++)
const int N = 1010;
int n,m,a[N],rd[N];
vector<int> edge[N];//存图
bool b[N],vis[N][N];//标记哪些是停靠站、是否已有边
queue<pair<int,int>> q; //车站编号、级别
inline void TopoSort(){
int res=0;//记录级别最大的即为答案
repn(i,1,n)
if(!rd[i]) q.push({i,1});//入度为0的,最低级的入队
while(!q.empty()){
auto x=q.front();
q.pop() ;
//cout<<x.fi<<' '<<x.se<<endl;
for(auto y:edge[x.fi])
if(--rd[y]==0){
q.push({y,x.se+1});
res=max (res,x.se+1);//取级别较大的
}
}
cout<<res<<endl;
}
void solve() {
cin>>n>>m;
//建图
repn(i,1,m){
memset(b,false,sizeof(b));
int len;
cin>>len;
repn(j,1,len)
cin>>a[j],b[a[j]]=true;
//连边、建图
repn(j,a[1],a[len]){//从a[1](起始站)到a[len](终点站)
if(b[j]) continue;//是停靠站
repn(k,1,len){//len个停靠站
if(vis[j][a[k]]) continue;//已有边
vis[j][a[k]]=true;
rd[a[k]]++;//该停靠站入度加1
edge[j].push_back(a[k]);
}
}
}
TopoSort();
}
signed main() {
//IOS;
int T=1;
//cin>>T;
while(T--) {
solve();
}
return 0;
}