目录
一、无监督学习
二、无监督学习和有监督学习的区别
三、K-Means
3.1数据分析
3.2k-meas算法
3.3数据正态化后k-means
3.4找最佳k(Elbow Plot)
四、k-means算法的优缺点
一、无监督学习
无监督学习是一种机器学习的方法,与监督学习不同,无监督学习不需要标记好的训练数据作为输入。在无监督学习中,算法根据输入数据的内在结构和模式来自动学习。这种学习的目标是发现数据中的隐藏模式、结构或关系,而不是根据预定义的标签进行分类或预测。无监督学习算法可以用于聚类、降维、异常检测等任务,可以帮助我们理解数据的特点和相似性,挖掘数据的潜在知识,以及发现数据中的异常情况。
二、无监督学习和有监督学习的区别
无监督学习和有监督学习是机器学习中两种常见的学习方式,它们的区别如下:
数据类型:无监督学习是在没有标签的情况下训练模型,只使用输入数据。有监督学习则需要标记好的输入数据和对应的输出标签。
目标:无监督学习的目标是发现数据中的潜在模式和结构,或者进行数据的聚类和降维等任务。有监督学习的目标是根据输入数据预测对应的输出标签。
训练方式:无监督学习中的训练是基于数据间的相似度或相关性进行的,例如聚类算法和关联规则挖掘等。有监督学习中的训练则是通过最小化预测结果与真实标签之间的差距来进行的。
性能评估:无监督学习的性能评估较为主观,通常依赖于领域知识或人工判断。有监督学习的性能评估则可以通过与真实标签进行比较来进行客观评估。
总的来说,无监督学习更侧重于数据的特征提取和发现,而有监督学习更关注于数据的预测和分类。
三、K-Means
k-means是一种常见的聚类算法,也是一种迭代的划分聚类方法。它的基本思想是将n个样本对象划分成k个簇,使得簇内的样本尽可能相似,而簇间的样本差异较大。具体实现上,k-means通过不断迭代的方式来更新簇中心,直到满足停止条件。在每次迭代中,k-means会计算每个样本与各个簇中心的距离,并将样本归到距离最近的簇中心所对应的簇中。然后,更新每个簇的中心为该簇内所有样本的均值,再次进行迭代直到收敛为止。
k-means算法的优点是简单、易于理解和实现,而且效果通常较好。它可以用于数据的聚类分析、图像压缩、文本挖掘等领域。然而,k-means算法需要预先设置簇的个数k,并且对于初始簇中心的选择比较敏感,有可能陷入局部最优。同时,k-means对于异常值和噪声数据比较敏感,可能会产生错误的聚类结果。因此,在实际应用中,需要根据具体问题来选择合适的聚类算法。
具体流程如下:
选择k个初始的质心,可以是随机选择或者通过其他方式选择。
将每个数据点分配给离它最近的质心,形成k个簇。
更新每个簇的质心,将质心更新为簇内所有点的平均值。
重复步骤2和步骤3,直到簇的分配不再发生变化或达到预定的迭代次数。
3.1数据分析
from sklearn.cluster import KMeans
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from matplotlib import pyplot as plt
%matplotlib inline
df = pd.read_csv("income.csv")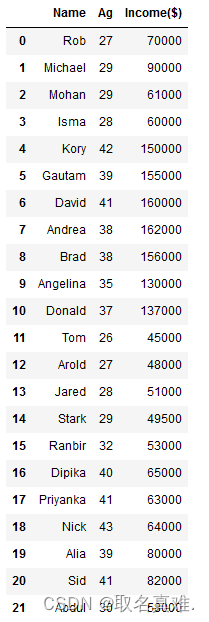
plt.scatter(df.Ag,df['Income($)'])#散点分布
plt.xlabel('Ag')
plt.ylabel('Income($)')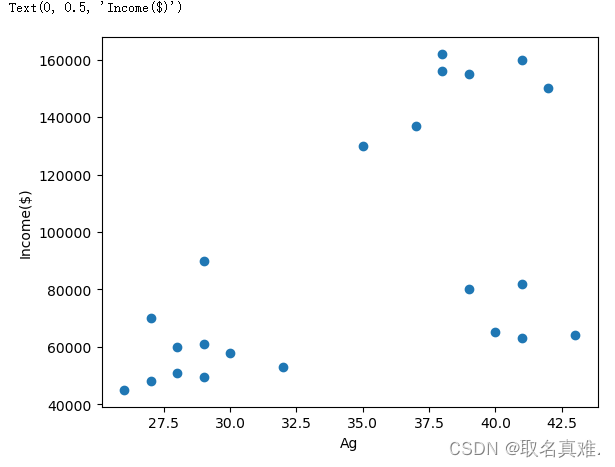
3.2k-meas算法
km = KMeans(n_clusters=3)#通过可视化图形,大致判断出3
y_predicted = km.fit_predict(df[['Ag','Income($)']])#基于两个变量kmeans
y_predicted#分成三组,各点的组别
#结果:array([2, 2, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1])
df['cluster']=y_predicted
km.cluster_centers_#中心点
'''结果:
array([[3.85714286e+01, 1.50000000e+05],
[3.20909091e+01, 5.61363636e+04],
[3.40000000e+01, 8.05000000e+04]])
'''df1 = df[df.cluster==0]
df2 = df[df.cluster==1]
df3 = df[df.cluster==2]
plt.scatter(df1.Ag,df1['Income($)'],color='green')#标识点
plt.scatter(df2.Ag,df2['Income($)'],color='red')
plt.scatter(df3.Ag,df3['Income($)'],color='black')
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],color='purple',marker='*',label='centroid')#中心点
plt.legend()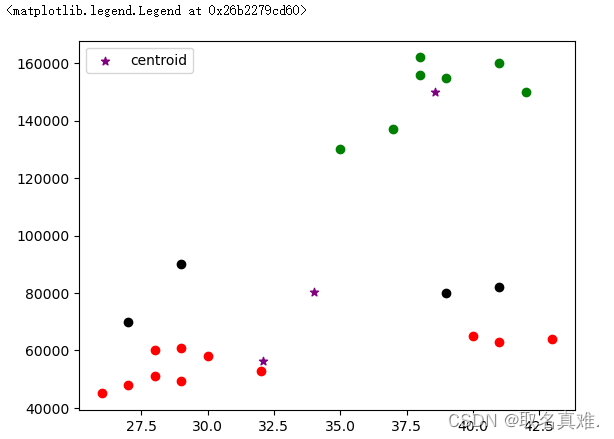
3.3数据正态化后k-means
#preprocessing using min max scaler(kmeans 对偏离值比较敏感,对数据进行进一步的正态化,标准化)
scaler = MinMaxScaler()
scaler.fit(df[['Income($)']])
df['Income($)'] = scaler.transform(df[['Income($)']])
scaler.fit(df[['Ag']])
df['Ag']= scaler.transform(df[['Ag']])
km = KMeans(n_clusters=3)#通过可视化图形,大致判断出3
y_predicted = km.fit_predict(df[['Ag','Income($)']])#基于两个变量kmeans
y_predicted#分成三组,各点的组别
#结果:array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 0])
df['cluster']=y_predicted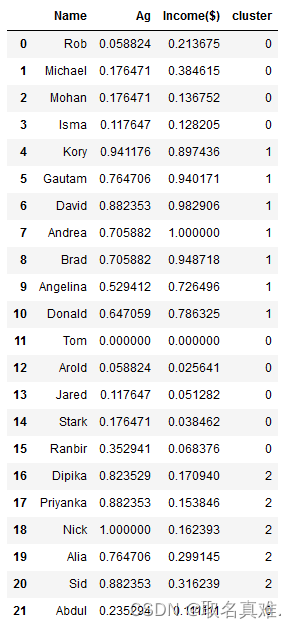
df1 = df[df.cluster==0]
df2 = df[df.cluster==1]
df3 = df[df.cluster==2]
plt.scatter(df1.Ag,df1['Income($)'],color='green')#标识点
plt.scatter(df2.Ag,df2['Income($)'],color='red')
plt.scatter(df3.Ag,df3['Income($)'],color='blue')
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],color='purple',marker='*',label='centroid')#中心点
plt.legend()#中心点要相对距离远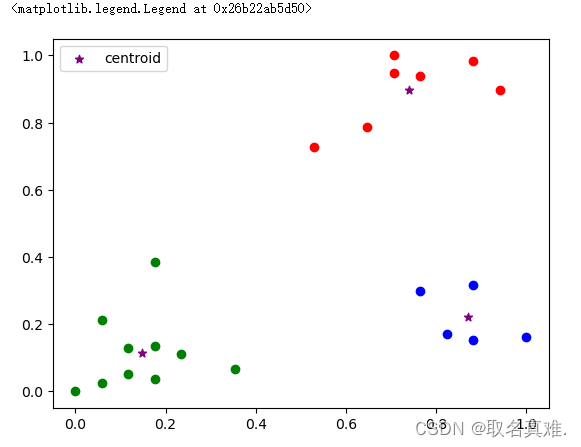
3.4找最佳k(Elbow Plot)
k-means的inertia(惯性)是一种评估聚类结果好坏的指标。它是每个样本到其最近聚类中心的距离的平方和,表示了聚类的紧密度。
具体地,假设有k个聚类中心和n个样本点,用d(i, j)表示样本点i和聚类中心j之间的距离。那么样本点i到其最近的聚类中心的距离可以表示为min{d(i,j)},而样本点i到所有聚类中心的距离的平方和可以表示为∑min{d(i,j)}^2。这个平方和就是inertia。
k-means算法的目标是最小化inertia值。较小的inertia值表示较紧密的聚类,说明聚类结果比较好。因此,在应用k-means算法时,我们通常会根据inertia值来评估不同聚类数量的效果,选择使inertia值最小的k值。
需要注意的是,inertia值受到数据集的大小和维度的影响。一般来说,数据集越大,inertia值越大;数据维度越高,inertia值越大。当使用inertia来比较不同聚类结果时,应该确保数据集和维度相对一致,或者使用其他调整的指标来进行比较。
在k-means算法中,Error Sum of Squares(ESS)是用来衡量聚类结果的紧密度的指标。它代表了每个数据点与其所属簇的中心点之间的距离的总和的平方。
具体地说,对于给定的数据集和k个簇,k-means算法迭代地将数据点分配到最近的簇,并通过重新计算每个簇的中心点来优化簇的位置。在每次迭代过程中,计算每个数据点与其所属簇的中心点之间的距离,并将这些距离的平方累加起来,得到ESS。
ESS的计算公式为:
ESS = Σ(distance(x, center))^2
其中,distance()代表计算两个点之间的距离的函数,x表示数据点,center表示簇的中心点。
k-means算法的目标是通过最小化ESS来找到最优的聚类结果,使得簇内的差异最小。在算法迭代过程中,不断优化簇的位置和分配数据点的过程就是为了降低ESS的值。
#Elbow Plot肘部
sse = []
k_rng = range(1,10)
for k in k_rng:
km = KMeans(n_clusters=k)
km.fit(df[['Ag','Income($)']])
sse.append(km.inertia_)#添加SSE(Error Sum of Squares)
sse
'''结果:
[5.476320414158672,
1.8312770324770151,
0.4446643017599456,
0.32491398139743455,
0.23872357386187126,
0.18333099202476363,
0.14326134350385375,
0.1105453573143515,
0.07977903629169414]
plt.xlabel('K')
'''
plt.xlabel('K')
plt.ylabel('Sum of squared error')
plt.plot(k_rng,sse)#很明显3为肘部的点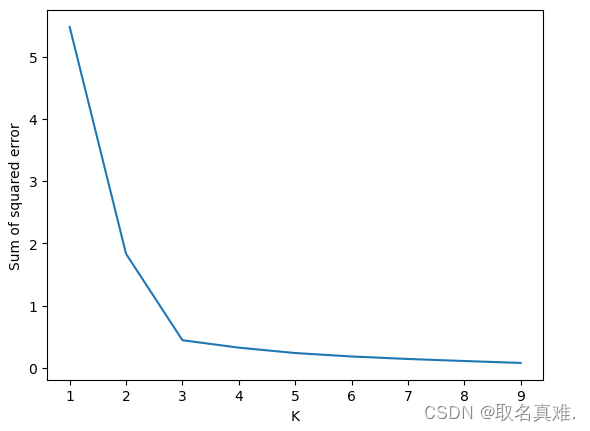
四、k-means算法的优缺点
K-Means算法的优点包括简单易实现、计算效率高、可扩展性强等。缺点包括对初始中心点的选择敏感、对异常值敏感、需要预先指定聚类数量等。
K-Means算法的优点:
- 简单易实现:K-Means算法是一种简单且易于理解的聚类算法,容易实现并且计算效率高。
- 计算效率高:K-Means算法的计算复杂度较低,适用于大规模数据集。
- 可扩展性强:K-Means算法可以很容易地扩展到高维数据集和大规模数据集。
K-Means算法的缺点:
- 对初始中心点的选择敏感:K-Means算法的聚类结果受初始中心点的选择影响较大,不同的初始中心点可能导致不同的聚类结果。
- 对异常值敏感:K-Means算法对异常值敏感,异常值可能会影响聚类结果。
- 需要预先指定聚类数量:K-Means算法需要预先指定聚类数量k,但在实际应用中,往往很难事先确定合适的聚类数量。