0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖，由本人亲自从底层编写、测试与文章配套的各个经典算法，不依赖于现有库，可以大大加深对算法的理解。

🚀详情：机器学习强基计划(附几十种经典模型源码)

---

在机器学习强基计划5-1：概率图开篇，机器学习中的图论总结(附思维导图)中我们介绍了什么是概率图模型，而概率图模型主要分为

• 有向无环概率图——经典的有向概率图为贝叶斯网络；
• 无向概率图——经典的无向概率图为马尔科夫随机场

在机器学习强基计划5-2：用一个例子通俗理解贝叶斯网络(附例题)中我们可以看到有向概率图贝叶斯网络已经能很好地表示推理工作，那为什么又需要引入无向概率图呢？本文从这个问题出发，逐步引出马尔科夫随机场

1 无向概率图

从典型的案例出发说明引入无向概率图的动机和必要性。

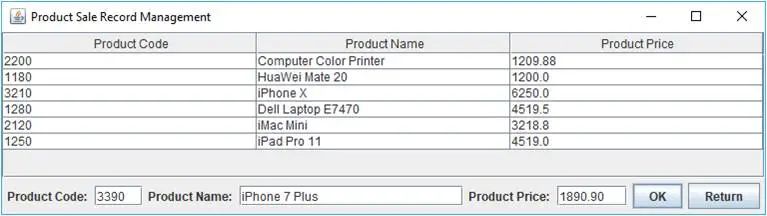
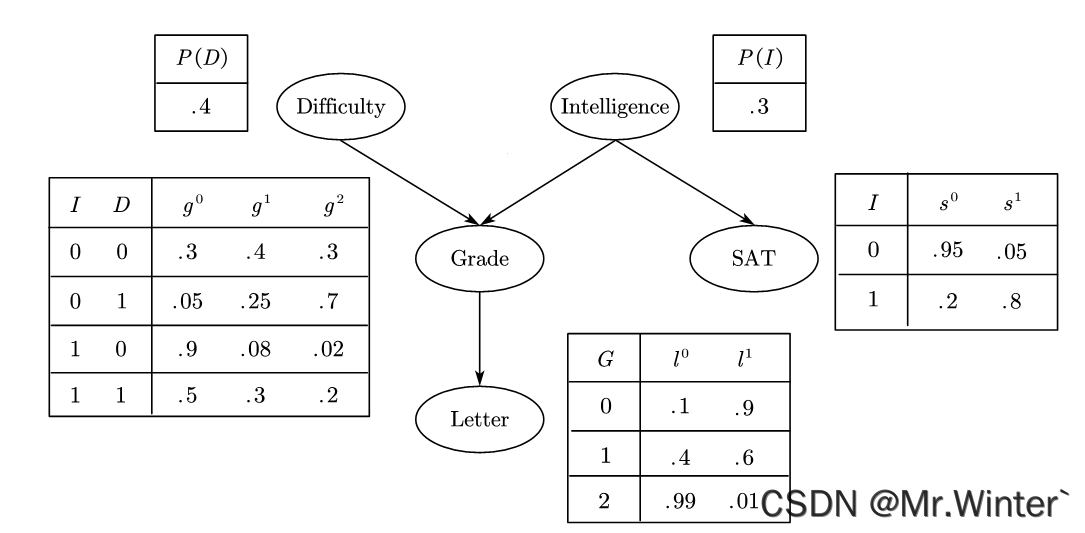
以贝叶斯网络为代表的有向概率图常用于表示随机变量间显式的因果关系，比如课程的难度会影响学生的成绩——课程越难成绩越低。

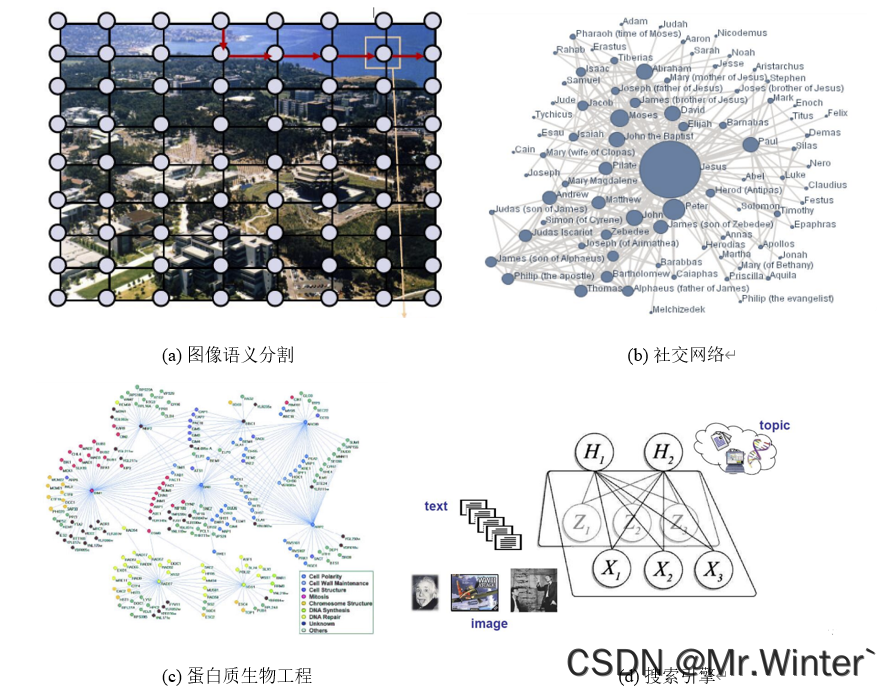
然而，在实际应用中，随机变量间可能存在对称的相互依赖，但不具有显式的因果性。这里举了很有代表性的四个例子：

• 图像分割
• 社交网络
• 蛋白质生物工程
• 搜索引擎

例如图像语义分割，每个像素被其近邻像素影响，同时也影响着近邻像素(当前像素语义是天空，那么近邻像素也很可能表示天空，反之亦然)；社交网络中用户的彼此交互等。依赖的对称性无法用有向图表达，否则会产生环，从而违反因果性，因此引入无向图刻画这类变量关系。

2 马尔科夫随机场

设同一样本空间下的一组随机变量构成集合，该集合每个元素按某种分布随机赋值，则该集合称为随机场(Random Filed)。马尔科夫随机场(Markov Random Field, MRF)是经典的无向概率图。与贝叶斯网络类似，马尔科夫随机场是一个偶对$\mathcal{H}=\left(\mathcal{G},P\right)$，即由网络拓扑结构以及概率分布两部分组成，其中

• 网络结构$\mathcal{G}=\left(V,E\right)$是无向图(Undirected Graphical Model, UGM)，$V$是图形中所有节点——随机变量的集合；$E$是所有连边——变量间相关依赖的集合。网络结构蕴含一系列独立性断言$\mathcal{I}\left(\mathcal{G}\right)$，这部分知识可以回顾机器学习强基计划5-3：图文详解因子分解与独立图I-Map(附例题分析+Python实验)

• 概率分布$P$是在网络结构$\mathcal{G}$上的因子分解，由Hammersley-Clifford定理可得
  $$P\left(X_1,X_2,\cdots ,X_m\right)=\frac{1}{Z^{\ast }}\prod _{Q\in {\mathcal{C}}^{\ast }}{\varphi }_Q\left({\mathbf{D}}_Q\right)$$
  其中${\mathcal{C}}^{\ast }$是图$\mathcal{G}$中全体极大团集合，${\mathbf{D}}_Q$是极大团$Q\in {\mathcal{C}}^{\ast }$对应的随机变量集合。因子${\varphi }_Q\left({\mathbf{D}}_Q\right)$在马尔科夫随机场中也称为团位势(clique potential)，势函数(potential function)的常见形式为
  $${\varphi }_Q\left({\mathbf{D}}_Q\right)=e^{-H_Q\left({\mathbf{D}}_Q\right)}$$
  其中$H_Q\left({\mathbf{D}}_Q\right)$是定义在团变量上的实值函数，根据实值函数定义划分不同的模型。

纯理论讲解可能有点枯燥，可以结合应用理解这些公式的含义：机器学习实战4：基于马尔科夫随机场的图像分割(附Python代码)

3 马尔科夫独立性

这部分和贝叶斯网络一样，用于简化联合概率。随机变量的影响在无向图中流动，当观测到某些变量时流动将受到阻塞。马尔科夫随机场中的变量独立性断言如下：

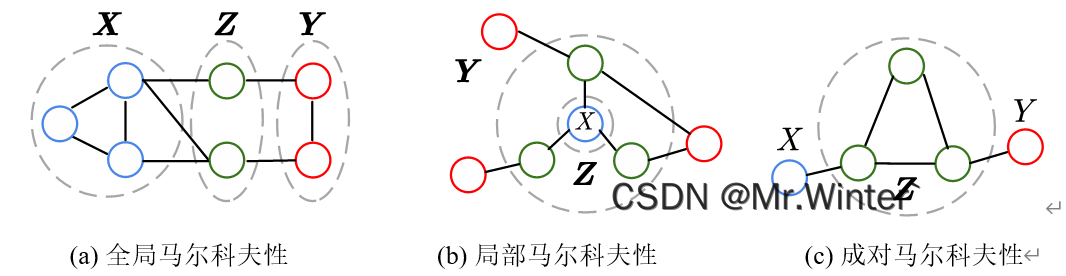
• 全局马尔科夫性(Global Markov Property)

  若给定观测变量集$\mathbf{Z}$时，任意两个节点$X\in \mathbf{X}$与$Y\in \mathbf{Y}$间没有路径，则称$\mathbf{Z}$在$\mathcal{G}$中分离$\mathbf{X}$与$\mathbf{Y}$，记为${\mathrm{sep}}_{\mathcal{G}}\left(\mathbf{X};\mathbf{Y}|\mathbf{Z}\right)$，全局独立性断言为

$$\mathcal{I}\left(\mathcal{G}\right)=\left\{\left(\mathbf{X}\perp \mathbf{Y}|\mathbf{Z}\right):{\mathrm{sep}}_{\mathcal{G}}\left(\mathbf{X};\mathbf{Y}|\mathbf{Z}\right)\right\}$$

• 局部马尔科夫性(local Markov property)

  局部独立性断言为给定变量$\mathbf{X}$的马尔科夫毯(Markov Blanket)， 条件独立于其余变量

I l ( G ) = { ( X ⊥ X − { X } − M B ( X ) ∣ M B ( X ) ) } \mathcal{I} _l\left( \mathcal{G} \right) =\left\{ \left( X\bot \mathcal{X} -\left\{ X \right\} -\mathrm{MB}\left( X \right) |\mathrm{MB}\left( X \right) \right) \right\} Il​(G)={(X⊥X−{X}−MB(X)∣MB(X))}

• 成对马尔科夫性(pairwise Markov property)

  成对独立性断言为给定所有其他变量，两个非邻接变量$X$、$Y$条件独立

I p ( G ) = { ( X ⊥ Y ∣ X − { X , Y } ) : X − Y ∉ G } \mathcal{I} _p\left( \mathcal{G} \right) =\left\{ \left( X\bot Y|\mathcal{X} -\left\{ X,Y \right\} \right) :X-Y\notin \mathcal{G} \right\} Ip​(G)={(X⊥Y∣X−{X,Y}):X−Y∈/G}

相应的概率图如下所示

4 例题分析

例1：如图所示马尔科夫随机场，求所有节点的联合概率

图所示马尔科夫随机场的极大团为 { x 1 , x 2 } \left\{ x_1,x_2 \right\} {x1​,x2​}、 { x 1 , x 3 } \left\{ x_1,x_3 \right\} {x1​,x3​}、 { x 2 , x 4 } \left\{ x_2,x_4 \right\} {x2​,x4​}、 { x 3 , x 5 } \left\{ x_3,x_5 \right\} {x3​,x5​}和 { x 2 , x 5 , x 6 } \left\{ x_2,x_5,x_6 \right\} {x2​,x5​,x6​}，则联合分布为

$$P\left(\mathbf{x}\right)=\frac{1}{Z}{\varphi }_{12}\left(x_1,x_2\right){\varphi }_{13}\left(x_1,x_3\right){\varphi }_{24}\left(x_2,x_4\right){\varphi }_{35}\left(x_3,x_5\right){\varphi }_{256}\left(x_2,x_5,x_6\right)$$

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《机器人原理与技术》
• 《机器学习强基计划》
• 《计算机视觉教程》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇