你真的懂树吗？二叉树、AVL平衡二叉树、伸展树、B-树和B+树原理和实现代码详解...

树（Tree）是一种相当灵活的数据结构（上一节已经详细讲解了基本的数据结构：线性表、栈和队列），你可能接触过二叉树，但是树的使用并不限于此，从简单的使用二叉树进行数据排序，到使用B-树或B+树设计数据库引擎，以及目前热门的人工智能机器学习都使用到树，例如决策树（Decision Tree）和随机森林（Random Forest），而AVL平衡树和伸展树是二叉树的优化版。树的实现原理算法比较复杂，即使能借助图片理解，算法代码依然比较困难，在第一节中（算法分析和算法设计）有详细提到算法设计的规则，使用自然语言或流程图，或者使用伪代码也可以，本文使用自然语言描述算法，可结合相关的图片进行理解，建议尽可能理解相关实例代码，并自己动手写。

一、树的基本概念

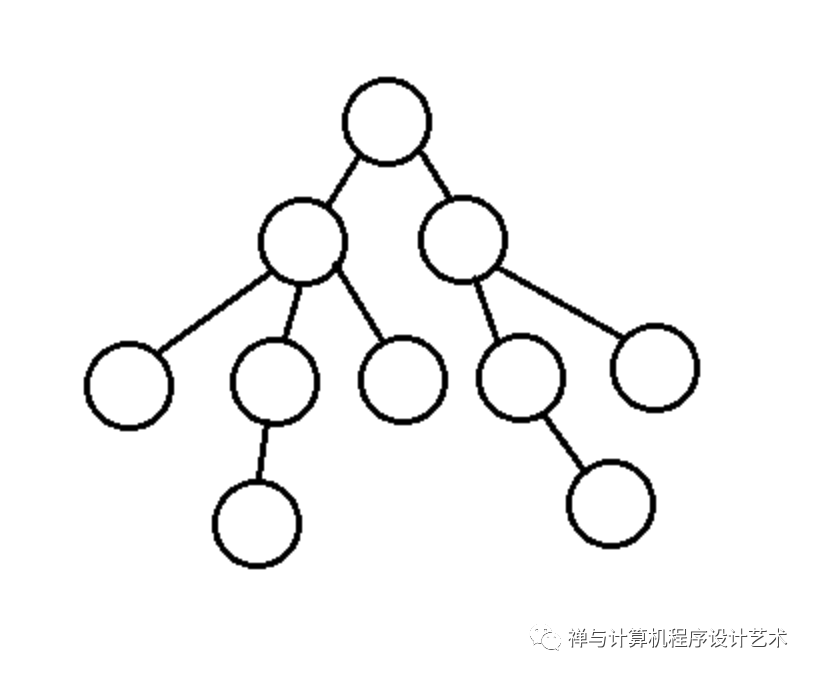
上图是一棵树，每个圆称为一个结点，最顶层的结点称为树根或根（Root），和根结点相连的结点称为根结点的儿子，以儿子为根的树称为子树，一棵树可能又0个或多个子树，子树是整棵树的局部树，最底层的结点称为树叶，树叶结点没有儿子或子树。

结点间的逻辑关系有：父亲结点（Parent Node），一个结点的上一个结点，根Root是所有子树的根的父亲；儿子结点（Child Node），一个结点的下面连线结点；兄弟结点（Sibling Node），具有相同父亲的结点。另外还有祖先结点和后代结点等，下图是对树的完整图解：

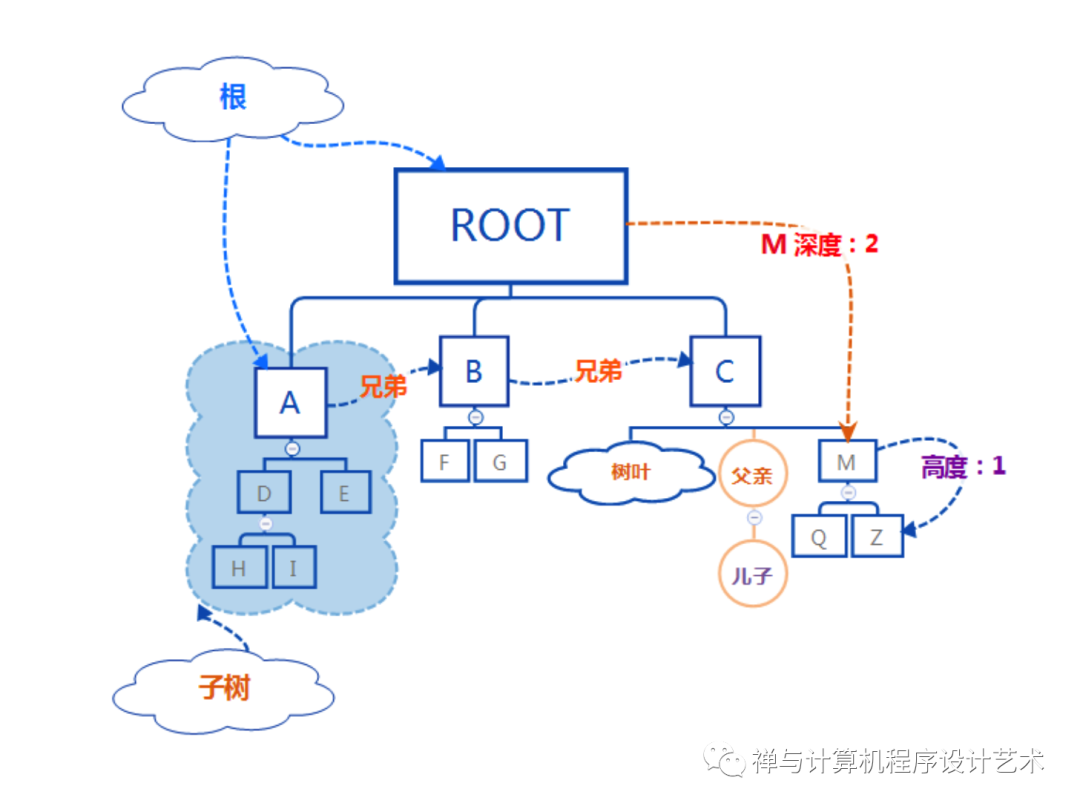
数的深度和高度：

1、边：一个结点到父亲的连线，路径长为两个连线结点间的边数，一个结点到自身的路径长为0。

2、深度：以树根结点为起始点，从根结点到一个结点的唯一路径长，结点的深度可以衡量遍历该结点的时间复杂度，树的深度等于最深树叶的深度。

3、高度：从一个结点到最长路径树叶的路径长，以最深树叶结点为结束点，树的高度等于根的高度，一棵树的深度等于树高。

一般来说，一个结点的儿子可使用指针指定，但是儿子的指针是如何指定的呢？使用关键字（Key），树结点的分布依据关键字的区间划分，一般的关键字可以是字符串（根据字符串的ASCII值进行比较）或整数或浮点数，或通过合理设计可以是其它复杂的逻辑形式。根据节点的关键字，小于关键字的结点在左边，大于关键字的结点在右边。这里的关键字和数据表的唯一键或主键类似，一般来说推荐使用唯一的关键字，这样可以避免重复的结点，关键字可使用数据域中的某一成员充当，或创建一个无关的关键字（但树并不严格要求需要有关键字，也可以无关键字）。

总的来说，设计一个树ADT，其数据结构至少要包含数据域、指针域和关键字域，如下代码是一个示例：

// 数据对象，一般业务数据
typedef struct post{
    unsigned int id;
    char *title;
    char *content;
} Post;

// 结点，包括数据域（可包含关键字），指针域
typedef struct pnode{
    int key; // 可自定义创建一个无关的关键字
    Post post; // 数据域（这里已包含关键字域）
    struct pnode *left; // 指针域，儿子结点
    struct pnode *right;
    struct pnode *parent;
    struct pnode *sblings;
} PNode;

// 树ADT对外接口
typedef struct ptree{
    PNode *root;
    unsigned int size;
} PTree;

二、树ADT的基本实现

树ADT的实现首先是数据结构的设计，其数据结构是相当简单的，像以上代码，数据结构包括数据域、关键字域和指针域，指针域包括父亲结点、一个或多个儿子结点和兄弟结点等，如下图的树，该树拥有左儿子和兄弟结点：

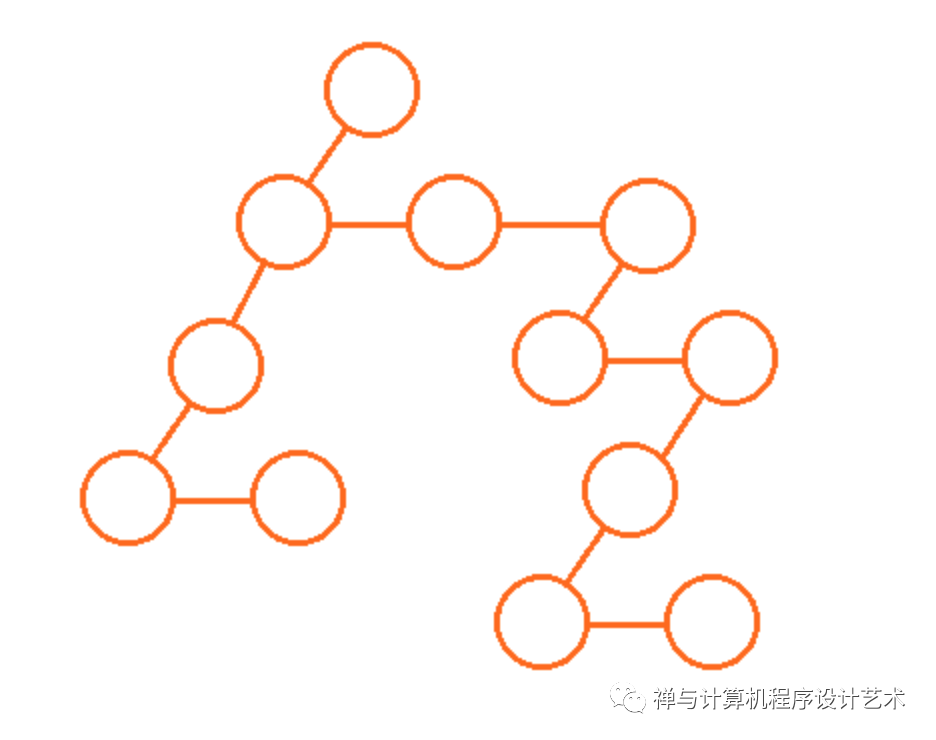
不过，树的算法操作则很是复杂，最复杂的算法包括遍历、删除和平衡，这里首先介绍遍历算法，删除和平衡算法下面会介绍。树的遍历包括深度优先遍历和广度优先遍历，下图是一个二叉树的两种遍历图解（下图的数字不作为关键字，仅作为结点的编号）：

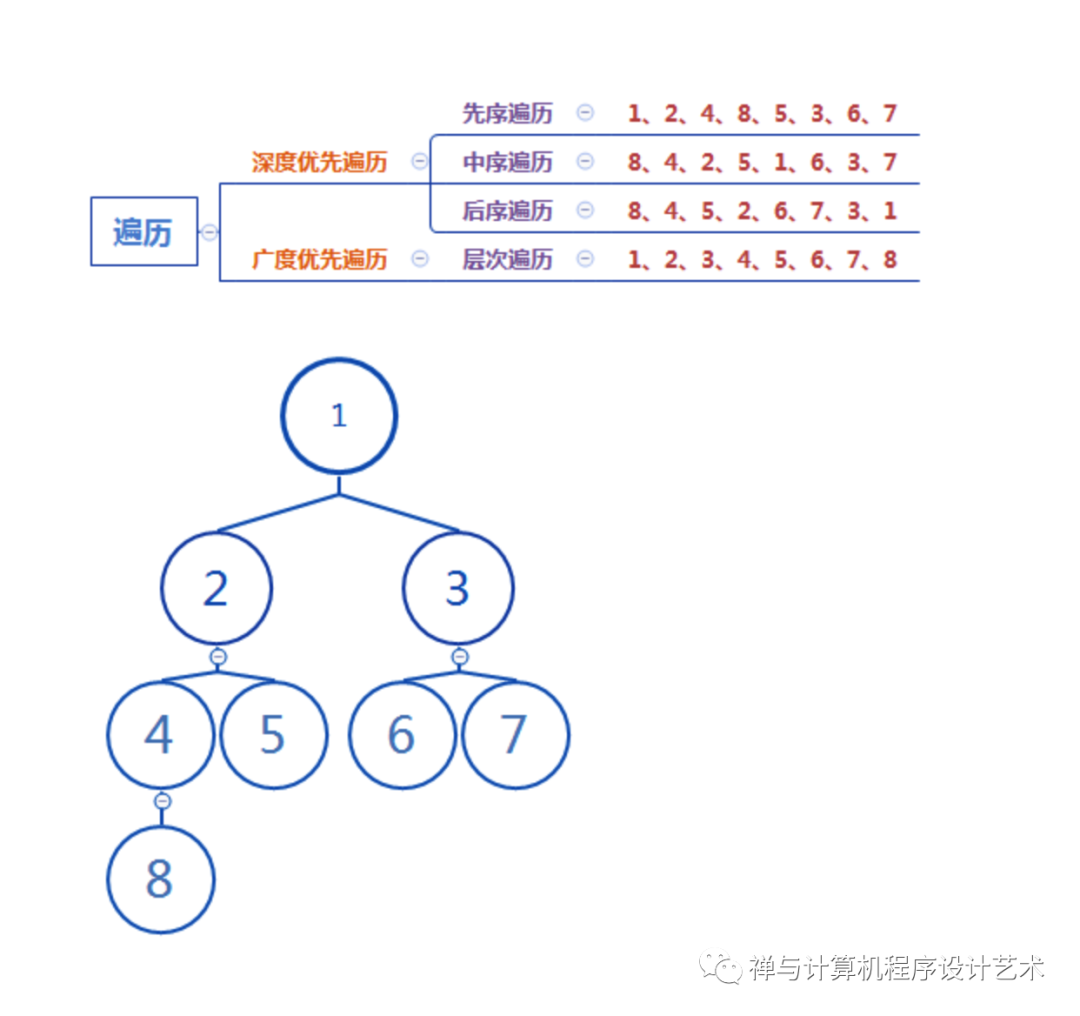
深度优先遍历：对于遍历树结点的算法，我们只需要集中在一个根结点及其儿子结点，深度优先遍历按分支路径遍历，先按一条分支路径遍历，再遍历其它路径，根据遍历根结点的顺序有三种顺序，这三种遍历都是以根结点为中心，主要使用递归算法，在处理根结点上为具体的算法，处理子树使用递归。

先序遍历：时间复杂度为O(N)，以根结点为中心，先处理根结点，再将根结点中存在的儿子结点分别取出来，儿子结点作为新的根结点，递归处理。

中序遍历：时间复杂度为O(N)，以根结点为中心，从根结点取出左右儿子结点，先处理左儿子，再处理根结点，后处理右儿子，将左右儿子作为新的根结点进行递归处理。

后序遍历：时间复杂度为O(N)，以根结点为中心，从根结点取出儿子结点，处理根结点，将儿子结点作为新的根结点递归处理。

深度优先遍历的实现方式有三种，递归算法，以根结点为中心进行递归遍历；迭代处理，可将递归算法转为迭代算法；借助栈进行处理，例如先序遍历的栈处理为：先将根结点入栈，出栈处理结点，将出栈的结点的儿子结点分别入栈，循环第二步。

广度优先遍历：按树的层次进行遍历，先访问第一层再访问第二层，广度优先遍历的实现方式借助队列：先将根结点入队，出队处理结点，将出队的结点的儿子分别入队，循环第二步。

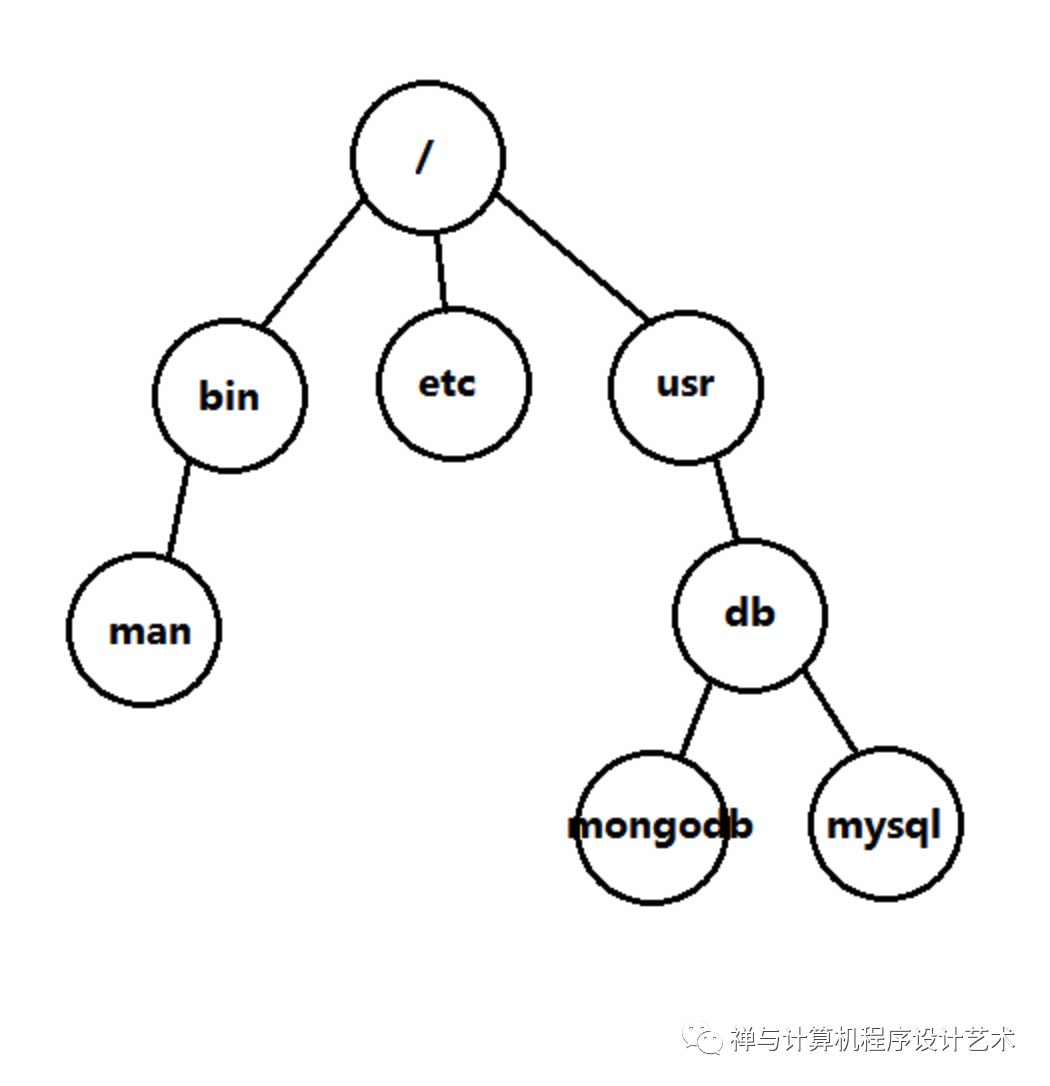
下面来看看树ADT的应用，树的一个结点可以存储n个关键字及其对应的n个数据对象，以及相应的n+1个指针。树可以实现操作系统的文件系统，例如Unix/Linux或Windows，一个文件夹内有多个文件或文件夹，这里统一称为文件，即一个文件内有多个文件，一个结点有多个儿子结点，如下图：

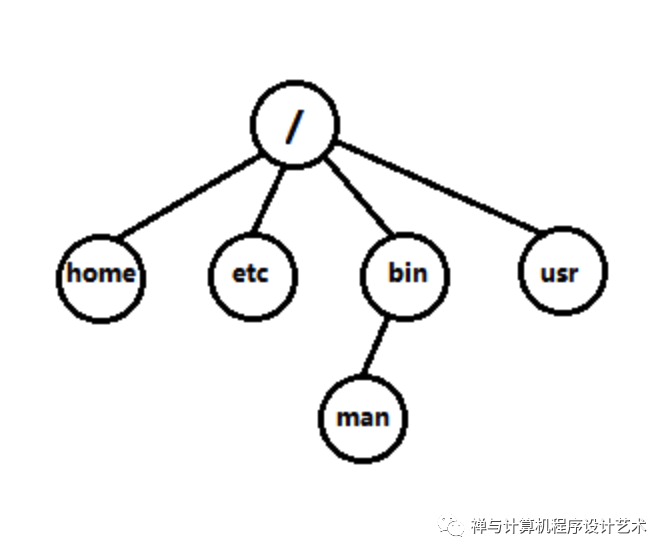
下面是文件系统ADT的声明代码，这里有两个树，其中一个树用于存储指针域，可以相对加快遍历儿子确定路径的速度，如果你使用的是Java或C++可以快速使用Java的treeSet和STL的set或map。

#define FILE_MAX_SIZE 10

// 文件数据实体
typedef struct file{
    char file_name[128]; // 关键字，同一目录中唯一
    char file_content[512];
    int is_directory;
} File;

// 文件结点
typedef struct tree Tree;
typedef struct fnode{
    File file;
//    int count; // 文件数量
//    struct fnode *files[FILE_MAX_SIZE]; // 文件数组（顺序表），一个目录最多FILE_MAX_SIZE个文件，
// 也可以使用链表存储，更好的方法可以使用一个二叉树存储（AVL树或伸展树，可以加快查找速度），如：
    Tree *files;
    struct fnode *parent;
} FNode;

// 二叉树ADT，作为一个数据容器，用于存储一个结点的所有儿子，不使用AVL平衡树或伸展树，查找速度最差的情况有可能是O(M)，
// M为儿子数，平均情况为O(logN)
typedef struct node{
//    char *file_name; // 关键字使用File中的文件名
    FNode *fnode; // int fnode
    struct node *left;
    struct node *right;
} Node;
struct tree{
    Node *root;
    int count; // 文件数量
};

// 文件树ADT
typedef struct ftree{
    FNode *root;
    int size;
} FTree;

// 二叉树ADT，数据容器
extern Tree *tree_init();
extern int tree_is_full(Tree *tree);
extern int tree_is_empty(Tree *tree);
extern int tree_add(Tree *tree, FNode *fnode);
extern FNode *tree_search(Tree *tree, char *file_name);
extern void tree_for_each(Tree *tree, void (*run)(FNode *));
extern int tree_clear(Tree *tree);


// 文件树ADT
extern FTree *ftree_init();
extern int ftree_is_full(FTree *ftree);
extern int ftree_is_empty(FTree *ftree);
extern int ftree_add(FTree *ftree, char directory[], File *file);
extern int ftree_is_exist(FTree *ftree, char file_name_absolute[]);
extern void ftree_traverse(FTree *ftree);
extern int ftree_clear(FTree *ftree);

写完后发现使用二叉树存储指针域比较难操作，用数组会方便一点，但是效率方面要差一些，这个普通二叉树一定程度上可以加快查找速度，该文件系统项目的完整源码可到github查看：https://github.com/onnple/filesystem，源码调用例子的树结构如下图：

三、二叉树查找树ADT

1、二叉树的基本概念

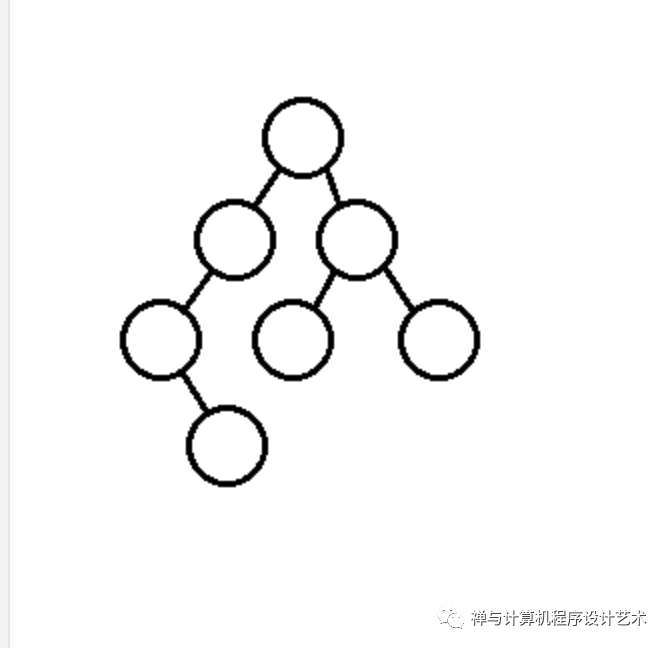
上面的例子已经用到二叉树，二叉树是一种每个节点最多只有两个儿子的树，儿子的排布按照：小于关键字在左边，大于关键字在右边，二叉树是树数据结构中最简单的一种树，二叉树实质也是图，树和图都是比较复杂以及技术要求较高的数据结构。二叉树深度的平均值为O(logN)，平均二叉树为根号N，这里要指出二叉树最理想的时候就是每个结点的左右子树高度相同，这个时候访问结点的最坏时间为O(logN)，但是这里的二叉树并不保证要满足这个条件，加入插入关键字从1到5，就会和链表一样了，这时候时间为O(N)，下面是一个普通的二叉树：

2、二叉树的数据结构和算法

二叉树的数据结构中至少需要提供：数据域、关键字域和左右儿子指针域，假设根结点的关键字值为X，则其左子树的所有值都小于X，右子树的所有值都大于X，对于等于X的重复情况可有如下处理：

（1）可简单作替换处理，遇到重复关键字直接覆盖原值；

（2）结点增加一个数据域记录结点的重复频率；

（3）使用辅助的数据结构，例如表或二叉查找树，用另外的数据结构存储重复值。

除了重复值覆盖处理，其它两种都比较复杂，所以设计关键字要尽量是唯一的，除非有其它不同的需求。

二叉查找树的所有基本算法的平均运行时间都是O(logN)，可见树或二叉树的在查找方面的效率比较好，其算法也比较复杂，其中要首先理解上面提到的两大遍历：广度优先遍历和深度优先遍历，在所有树中都可以使用。

二叉树插入数据：使用先序遍历，即先在根结点上做判断是否插入数据，后再处理左右儿子，相对没那么复杂。

二叉树查找数据：查找某个元素使用先序遍历的形式，查找最大值只需要往最右边查找，查找最小值只需要往最左边查找。

二叉树删除数据：除了上面提到的树遍历比较难之外，删除数据比遍历更复杂。对于删除所有的结点，使用后序遍历，由下至上释放数据，对于只删除一个结点的操作，有以下几种情况：

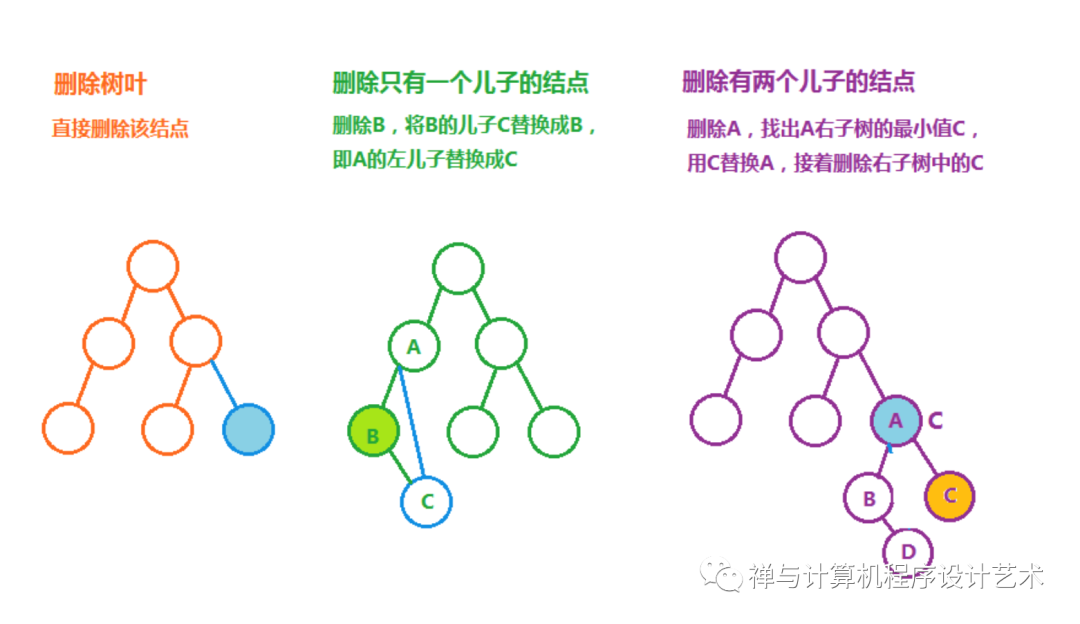
（1）结点是树叶：直接删除本结点，然后从父结点删除该结点的指针；

（2）结点只有一个儿子：将儿子结点替换该结点；

（3）结点有两个儿子：找出该结点右子树的最小值，将最小值替换该结点，然后删除最小值所在的结点，转换成删除只有一个儿子或树结点。

具体算法为：遍历到目标结点，以该结点的右儿子为根的子树，找出该子树的最小值，用最小值替换目标结点。该算法可提高删除效率，但是上次操作会导致左子树深度比右子树深，大量删除操作会导致二叉树左移。

（4）逻辑删除：这个方式在数据表删除数据也用到，在二叉树删除中，子啊结点中添加一个频率数据域，或在节点添加删除记号。

3、二叉查找树的应用

树的应用非常广，是一个相当之有用的数据结构，除了上面提到的以及文件系统的代码实例，还有其它用处，例如排序，路由算法，语法树或表达式树、游戏场景管理或设计和图片合成等，路由算法可用于分布式服务器，游戏相关的都大量用到树或图。树的显著特点就是快速排序和快速查找，因此在使用树的时候也不必拘谨于定义，下面举两个例子，一个是排序的简单实例，另一个是实现表达式树，表达式树又称为抽象语法树AST。

使用二叉查找树实现快速排序：因为二叉树本身就具有排序的特性，因为下面的实例不仅仅集中于排序，重点还要注意遍历、插入和删除数据，这几个都是难点，建议分析代码动手写多几次，下面是头文件二叉查找树ADT声明：

// 数据对象
typedef struct movie{
    int id; // 关键字，唯一键，按id排序
    char name[128];
    char about[512];
} Movie;

// 树结点
typedef struct mnode{
    Movie movie;
    struct mnode *left; // 左儿子
    struct mnode *right; // 右儿子
} MNode;

// 二叉树ADT
typedef struct stree{
    MNode *root;
    unsigned int size;
} STree;

// 二叉树算法操作声明
extern STree *stree_init();
extern int stree_is_full(STree *stree);
extern int stree_is_empty(STree *stree);
extern MNode *stree_get_max(STree *stree);
extern MNode *stree_get_min(STree *stree);
extern int stree_add(STree *stree, Movie *movie);
extern int stree_delete_by_id(STree *stree, int id);
extern int stree_clear(STree *stree);
// 排序：按id升序排列每个元素分别执行一个函数
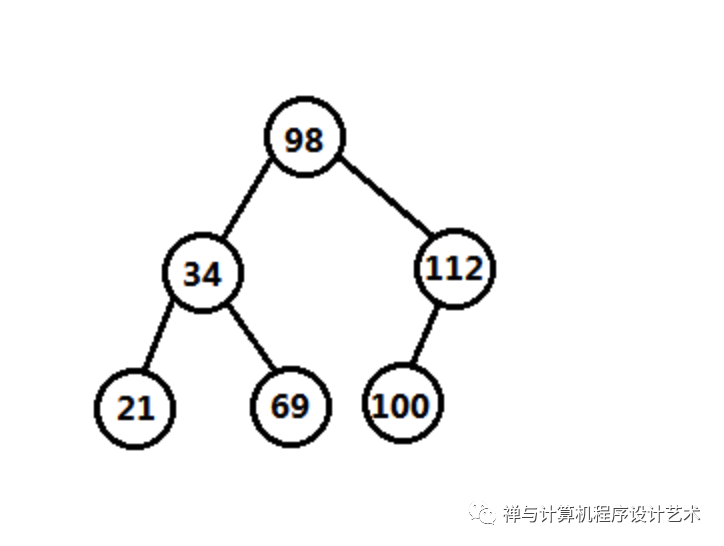
extern void stree_process(STree *stree, void (*process)(MNode *mnode));

以上是标准的二叉查找树实现方式，完整的实现源码可以到github查看：https://github.com/onnple/stree，源码主要都是使用递归方式实现，特别要注意：实际使用时尽量或者干脆不要用递归方式写代码，递归算法会因N的变大而耗费过多内存，最好习惯使用迭代或将递归转为迭代，while或for迭代，for的方式是这样for(;;)，迭代的检查元素主要是root根结点，之后的例子会尝试部分使用迭代。以上代码的调用实例的树形状如下：

实现表达式树或抽象语法树BST：表达式树主要在编译器中用到，词法分析或语法分析，用于解释文本，如代码，另外最简单计算器到强大的数学计算软件都有用到，主要就是翻译文本，例如还有自然语言处理。

这里仅讨论数学表达式的计算，例如代数表达式a*b +ｃ，转换成表达式树，其数据结构至少包含指针域，关键字域和数据域，树叶用于存储操作数，其它结点为操作符，如下图：

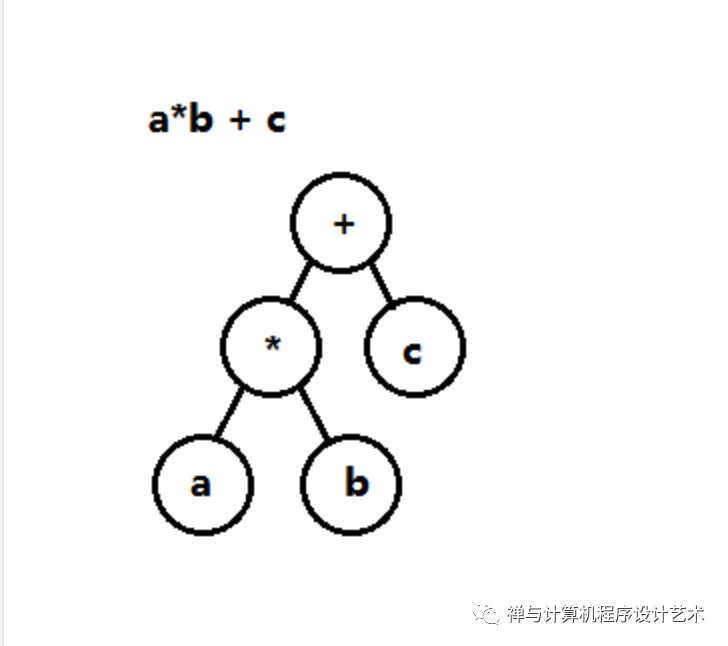
表达式有三种表示方式：前缀表达式，中缀表达式和后缀表达式，分别对应三种遍历方式，我们这里只需要关注中缀表达式和后缀表达式，ａ×ｂ＋ｃ则是中缀表达式，而它的后缀表达式为ａｂ×ｃ＋，中缀表达式作为我们的书写使用习惯，但是为什么需要后缀表达式呢？因为后缀表达式方便我们构造树，也方便计算，例如ａｂ×ｃ＋，将ａ和ｂ分别入栈，遇到运算符将栈中的两个元素弹出运算，将结果压入栈。所以我们的整体逻辑是：将中缀表达式转为后缀表达式，后缀表达式转为表达式树，进行数学运算的时候使用后缀遍历，所有转换或运算都需要借用栈。下面说明一下这两种转换的算法：

中缀表达式转为后缀表达式：以运算符优先级为依据，遇到操作数输出，遇到运算符压入栈，如果发现栈顶的运算符优先级大于当前运算符，则弹出栈中的所有运算符到输出，括号运算符(只有遇到成对)才全部弹出，一直弹到(，括号()不放到输出中。

后缀表达式转为表达式树：将操作符和操作数的结点地址压入栈中，遇到操作数入栈，遇到操作符将操作数弹出作为操作符的右左儿子结点，将操作符地址入栈，最后一个操作符为根结点。

这里的实例为简单起见仅仅是实现一个二叉表达式树，程序的一个参考的完整设计流程如下：

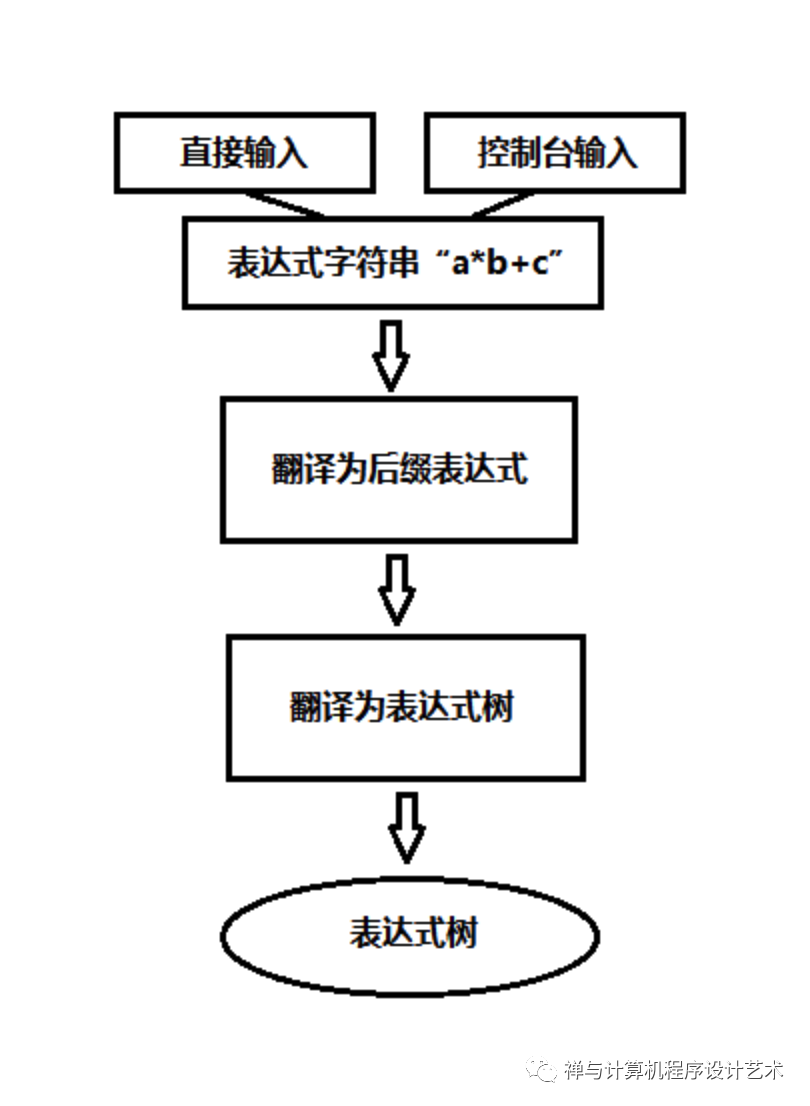
由于对表达式的词法分析和语法分析比较复杂，这里从简，只做简单的语法检查，下面是表达式树ADT的声明代码，其中有对表达式规则的说明：

/**
 * 表达式：-30.ax^2.5+3x - 5b
 * 表达式规则：a^0-64.a.b4
 * 1、运算符仅限于+ - * / ^ ( )，（字符还包括小数点.）
 * 2、代数式只能使用数字和字母，（字符、数字、运算符、小数点、空格）
 * 3、数字可使用正负数、整数和浮点数，字母只可使用"单字符"作为标识符，空格分隔表示相乘，
 * 例如ab表现和a b表示a*b，数字和字符相连表示相乘，如3a/a3=3*a，数字和数字空格表示相乘3 5=3*5
 * */

/**
 * 词法分析: 字符流转为记号流（token）
 * 语法分析：输出抽象语法树
 * 处理流程：
 * 1、语法规则：
 *      非法字符
 *      全为字符、数字、运算符、小数点、空格，或组合，错误
 *      ()配对
 *      小数点.配对：数字和小数点.的组合中只能有一个小数点，以小数点开头表示纯小数，如.5表示0.5，数字后面的小数点属于数字本身
 *      字母和字母间的小数点，错误
 *      连续重复的运算符，错误
 *      尾部运算符，错误
 * 2、初步转化：
 *      将字母和字母、字母和数字、数字和数字之间的空格用*替换；
 *      去除所有空格
 * 3、转换成后缀表达式
 * 4、生成表达式树：
 *      先分词，转换成一个个token
 * */

#define TOKEN_MAX 16

// 单项式
typedef struct monomial{
    int priority; // 数字的优先级为-1，字母为0，()为20，+-为13，*/为14，^为15
    char token[TOKEN_MAX];
} Monomial;

// 表达式树结点
typedef struct enode{
    Monomial monomial;
    struct enode *left;
    struct enode *right;
} ENode;

typedef int Cell;
typedef struct cnode{
    Cell cell;
    struct cnode *next;
    struct cnode *prev;
} CNode;

// 表达式树ADT
typedef struct exp{
    ENode *root;
    unsigned int size;
} Exp;

// 栈ADT
typedef struct cstack{
    CNode *head;
    CNode *tail;
    unsigned int size;
} CStack;

// 算法操作声明
extern CStack *cstack_init();
extern int cstack_push(CStack *cstack, Cell cell);
extern Cell cstack_pop(CStack *cstack);
extern Cell cstack_peek(CStack *cstack);
extern int cstack_clear(CStack *cstack);

extern Exp *exp_init();
extern int exp_load(Exp *exp, char str[]);
//extern int exp_add(Exp *exp, Monomial *monomial);
extern void exp_traverse(Exp *exp);
extern int exp_clear(Exp *exp);

以上实现表达式树的程序中重点是利用了栈，完整实现代码可到github上查看：https://github.com/onnple/expression_tree，该程序使用了两次栈，在树数据结构上面，使用栈和队列会比较方便。

四、AVL平衡二叉树

1、AVL平衡二叉树基本的概念

AVL树是一种自平衡树，它也是一个二叉树，所有树都是基于二叉树的概念，下面讨论的树，都是最基本二叉树的扩展。平衡二叉树相比普通二叉树，普通二叉树是不要求结点平均分布，最差的情况会造成O(N)的运行时间，如下图：

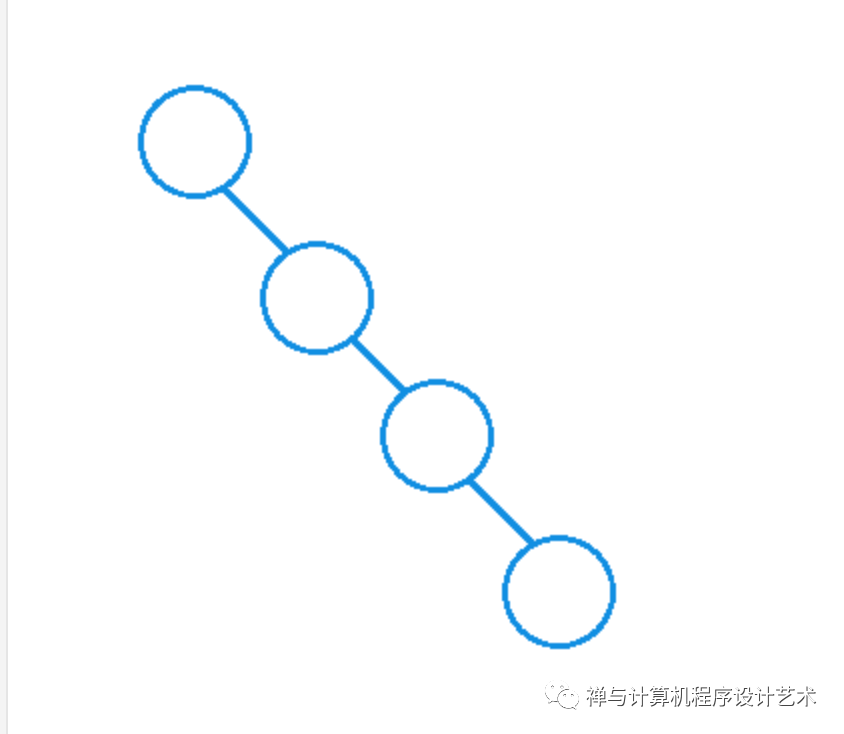
这就体现不到二叉树的查找优点了，为了解决这个问题，我们需要对二叉树的构造有所要求，最理想的情况就是要求一个结点的左右子树的高度相同，但是这个要求太严格，因此我们要求每个结点的左右子树的高度最多相差1，这样AVL树可以保证最坏情况为O(logN)。

AVL树在实现上需要在每个结点中保留高度信息，或者使用平衡因子（Balanced Factor），简称BF，每个结点的平衡因子等于左子树的高度减去右子树的高度，因此平衡值只有三种-1，+1和0。AVL树主要是在增加或删除结点后需要重新计算平衡因子，调整树的结构使其重新平衡，下面是一个例子，将2插入3的左边会造成结点4和结点5失衡：

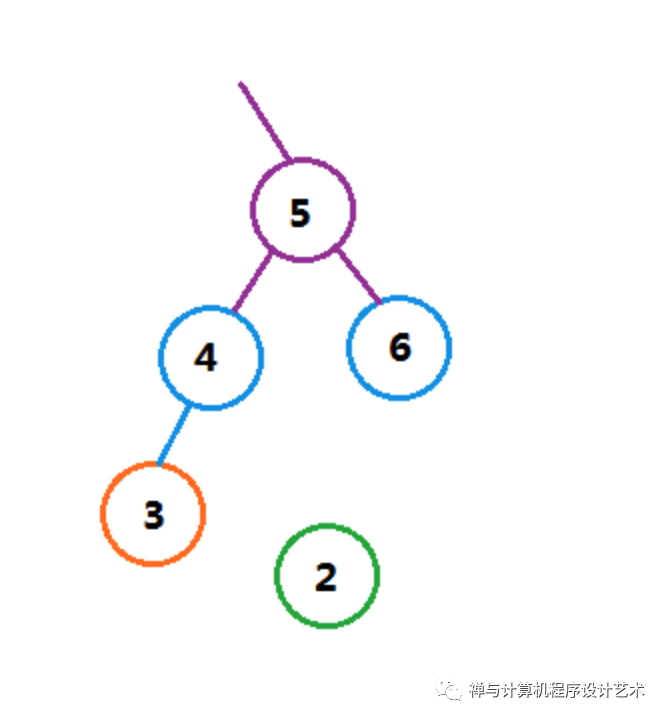
让AVL树重新平衡的操作叫做旋转（Rotate），旋转操作是树的基本操作也是其中一个难点，对于旋转，使用结点上下移动反而会好理解一点，失衡结点的BF为2或-2，注意这个失衡结点一般取的是最小失衡结点，如上图取的是结点4，因为高度的计算是从该结点到最深子树的路径长，所以将失衡结点下移一层即可达到平衡，如下图，每一层的左右结点作为空穴，作为结点上下移动可被占据的位置。

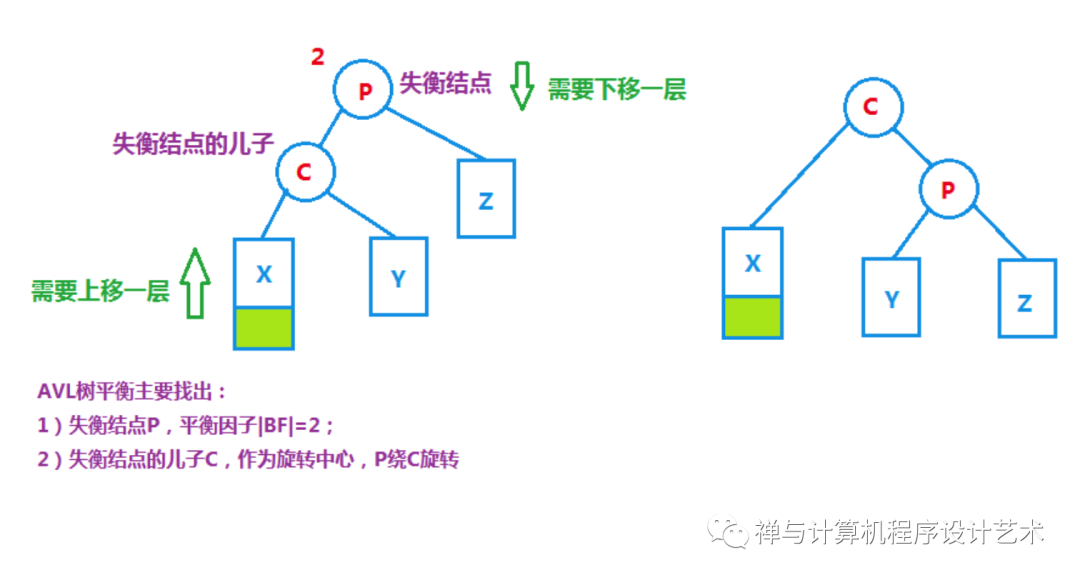
2、二叉树不平衡的四种情况

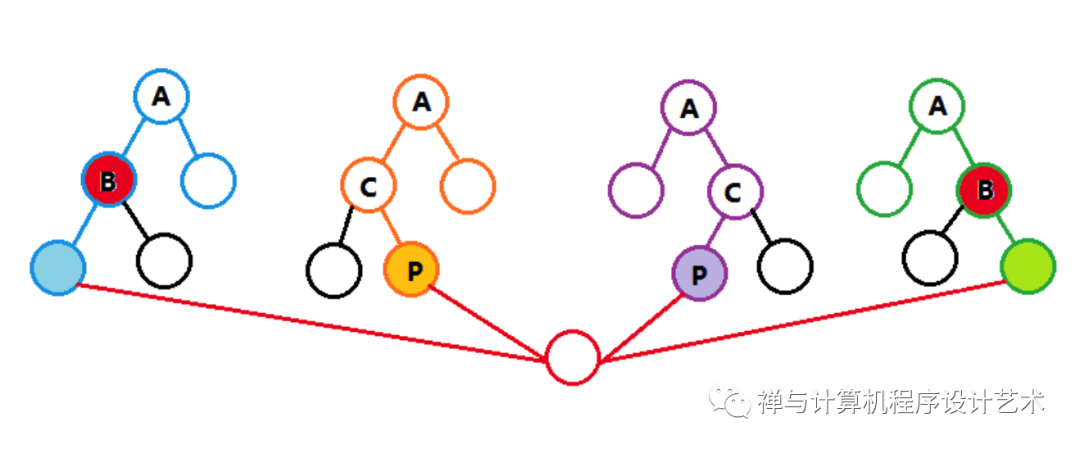
首先要确定中心结点，即最小失衡结点A，其平衡因子的绝对值为2，主要有四种不平衡的情况：

（1）在A的左儿子B的左子树插入，又称为LL；

（2）在A的左儿子C的右子树插入P，又称为LR；

（3）在A的右儿子C的左子树插入P，又称为RL；

（4）在A的右儿子B的右子树插入，又称为RR。

要记住两个重要节点，一个是失衡结点，另一个是失衡结点的儿子，该儿子在失衡路径上，旋转操作则是依据失衡结点的儿子为中心，对失衡结点进行下移动。在这四种失衡情况中（1）和（4）是一样的，（2）和（3）是一样的，前者使用单旋转，后者使用双旋转。

3、AVL树单旋转和双旋转

在进行旋转操作时，首先要找到最小失衡结点，判断失衡的类型，然后选择旋转的类型，如何判断呢？根据上面的图片中的结点A，BF为2确定为左儿子左边L，根据左儿子的BF为-1，则确定为R，此时属于不平衡情况（2），使用双旋转，下面详细介绍单旋转和双旋转的四种旋转方式。

（1）LL右旋转

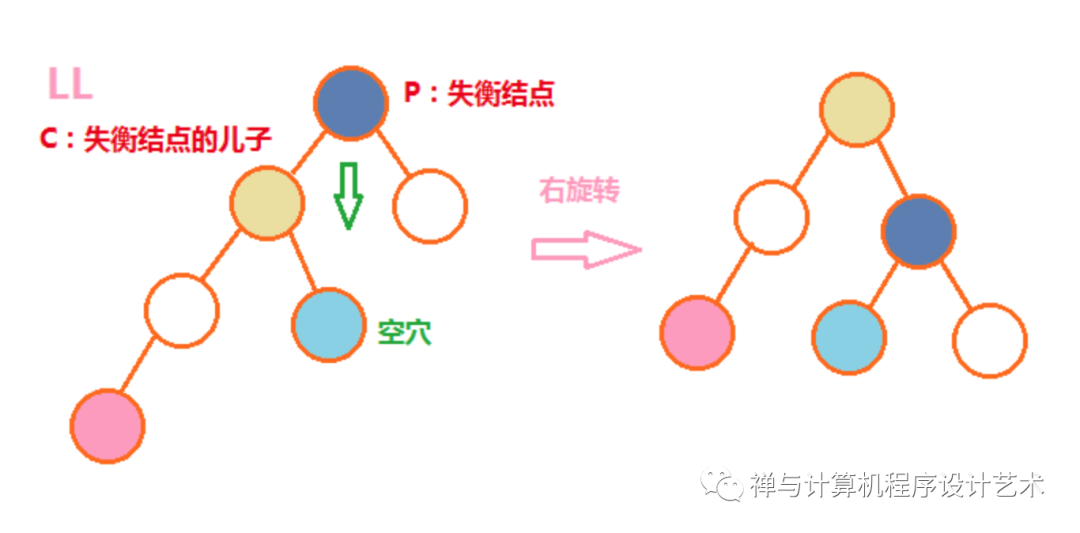
P下移，占据C的右儿子空穴，C的右儿子称为P的左儿子。

（2）RR左旋转

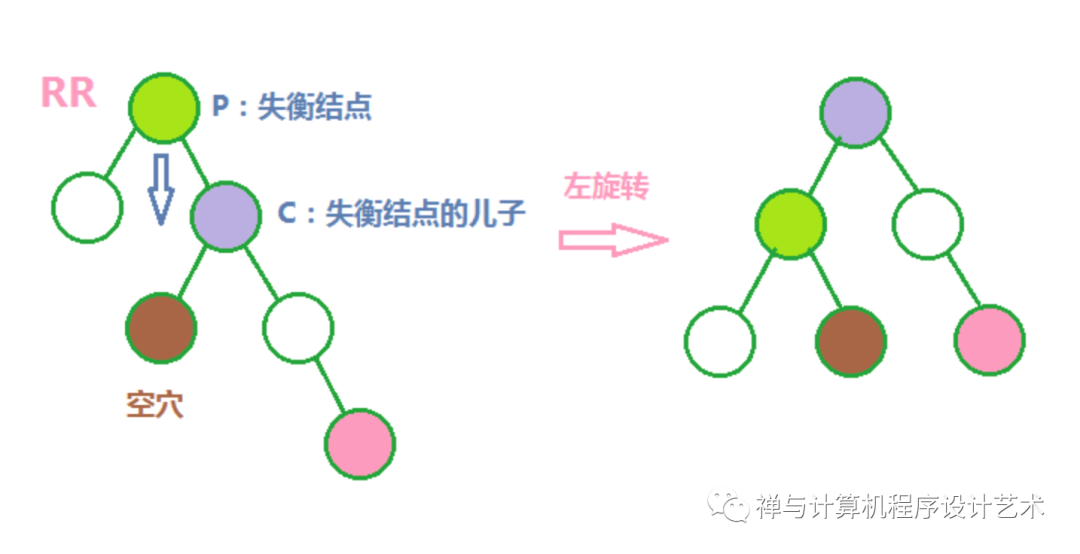
P下移，占据C的左儿子空穴，C的左儿子作为P的右儿子。

（3）LR左右旋转

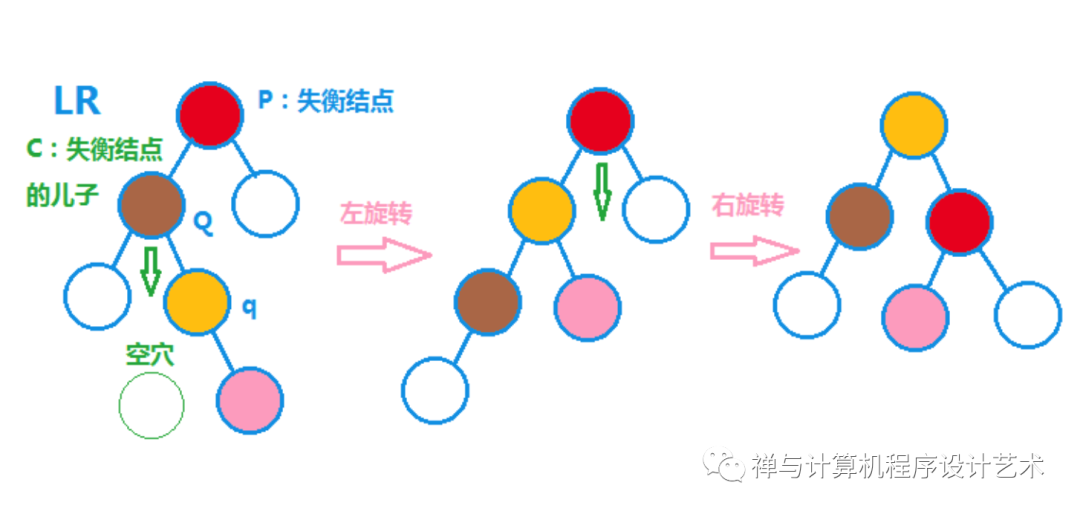
双旋转分为两步：左旋转，以P的儿子C作为失衡结点，Q的右儿子q，Q下移，占据q的左儿子，q的左儿子左儿子作为Q的右儿子，q作为P的左儿子。

右旋转，P下移，作为p的右儿子，q的右儿子作为P的左儿子。

（4）RL右左旋转

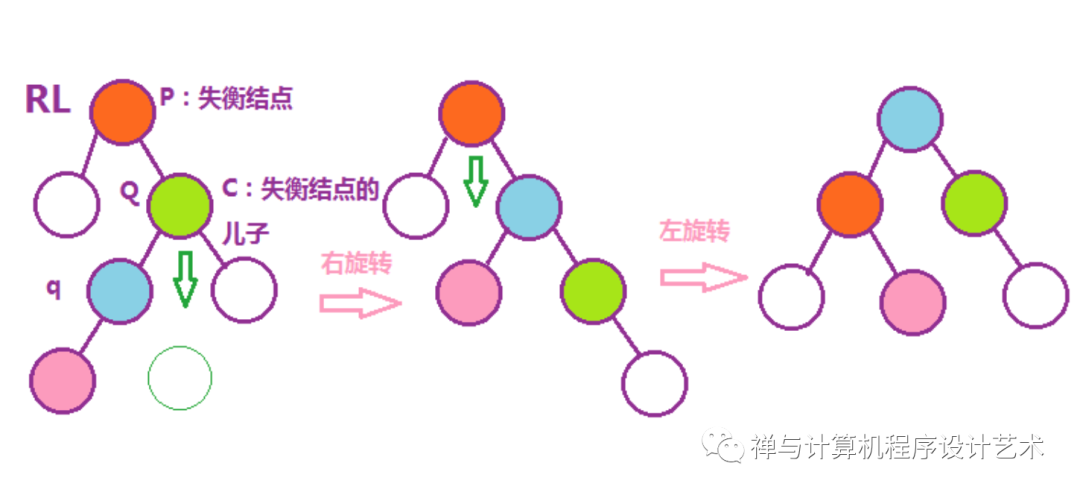
右旋转，P的右儿子C作为新的失衡结点Q，Q的左儿子q，Q下移，作为q的右儿子，q的右儿子作为Q的左儿子，q作为P的右儿子。

左旋转，P下移，占据q的左儿子，q的左儿子作为P的右儿子。

4、AVL平衡二叉树的数据结构和算法实例

平衡旋转操作主要是增加数据和删除数据的时候进行，代码实现上，其数据结构需要包含数据域，指针域，包括左右儿子或父亲结点，关键字域，用于排列结点，结点高度或平衡因子BF，空树的高度为-1，叶子结点的高度为0。

下面是AVL树的ADT声明：

// 数据对象
typedef struct user{
    unsigned int id; // 关键字
    char username[128];
    char password[128];
} User;

// 结点
typedef struct avlnode{
    User user; // 数据域
    struct avlnode *left; // 左右儿子
    struct avlnode *right;
    int height; // 高度
} AVLNode;

// AVL树ADT对外接口
typedef struct avltree{
    AVLNode *root;
    unsigned int size;
} AVLTree;

// 算法声明
extern AVLTree *avltree_init();
extern int avltree_is_full(AVLTree *avltree);
extern int avltree_is_empty(AVLTree *avltree);
extern int avltree_add(AVLTree *avltree, User *user);
extern int avltree_delete_by_id(AVLTree *avltree, unsigned int id);
extern AVLNode *avltree_get_by_id(AVLTree *avltree, unsigned int id);
extern void avltree_traverse(AVLTree *avltree, void (*traverse)(AVLNode*));
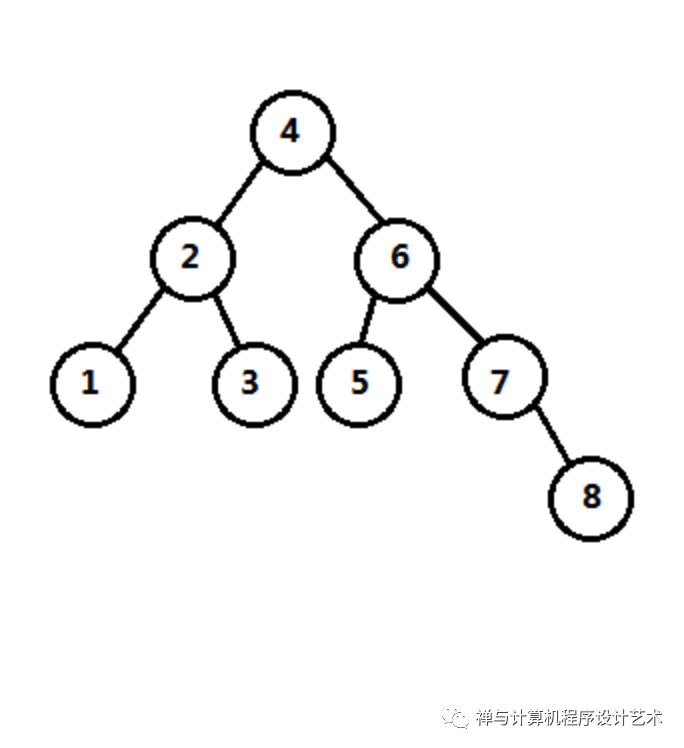
extern int avltree_clear(AVLTree *avltree);

完整代码可以到github查看：https://github.com/onnple/AVLTree，平衡二叉树的实现难点在于旋转，在该实例代码中，在进行删除和添加结点经过的路径上的每个结点检查高度，发现失衡结点进行旋转，并对每个结点进行高度更新，同样，在参与旋转结点中也需要对结点进行高度更新，其中代码调用实例的例子树结构如下图：

五、伸展树（Splay Tree）

1、伸展树的基本概念

AVL树在每次删除或添加结点时都需要使用旋转操作平衡二叉树，以获得最好的查找效率，伸展树是另一种二叉树，它不需要高度或平衡因子这些平衡信息。伸展树使用另一种方式实现高效率的查找，不平衡但要求每次操作的那个结点旋转到根结点上来，这样下次查找它就能达到最快效率了，这是根据计算机的局部原理，当一块数据被访问后，此后段时间内也会该数据或附近的数据也会被再次用到。这也就是说，进行增加、删除、查找等操作都需要将本次操作的结点或附近结点旋转到根结点上，可对所有操作都调整，或只针对查找进行调整。

伸展树进行M次操作，其时间复杂度为O(M logN)，而普通二叉树最坏情况为O(N)，连续M次操作为O(M*N)。如果一个算法M次操作的时间为O(MF(N))，则O(F(N))称为该算法的摊还时间或摊还代价，伸展树的摊还代价为O(logN)。

2、伸展树的实现原理

综上，伸展树不需要AVL树的平衡信息，高度或BF，它是一个普通二叉查找树，它的出发点是：频繁查找一个深结点X，会造成花费的时间过多，采取的办法是：将树在X处展开，将该结点旋转到根结点，自下向上单旋转，对访问路径上的每个结点和父结点进行单旋转，这样频繁访问结点即可大大减少时间，但是执行M次操作仍然至少需要M*N的时间（最坏情况单链表为N）。

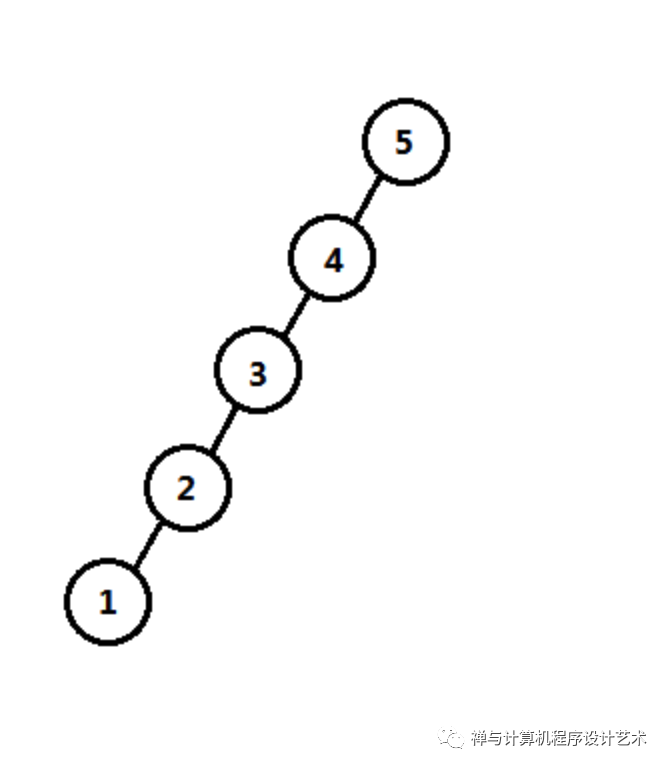
伸展树在实现上可使用上面说的单旋转，根据目标结点，全部使用单旋转，但是效率并不好，例如单链表的情况，依次插入1、2、3、4、5，其效率并不好，结点4深度依然比较深，如下图：

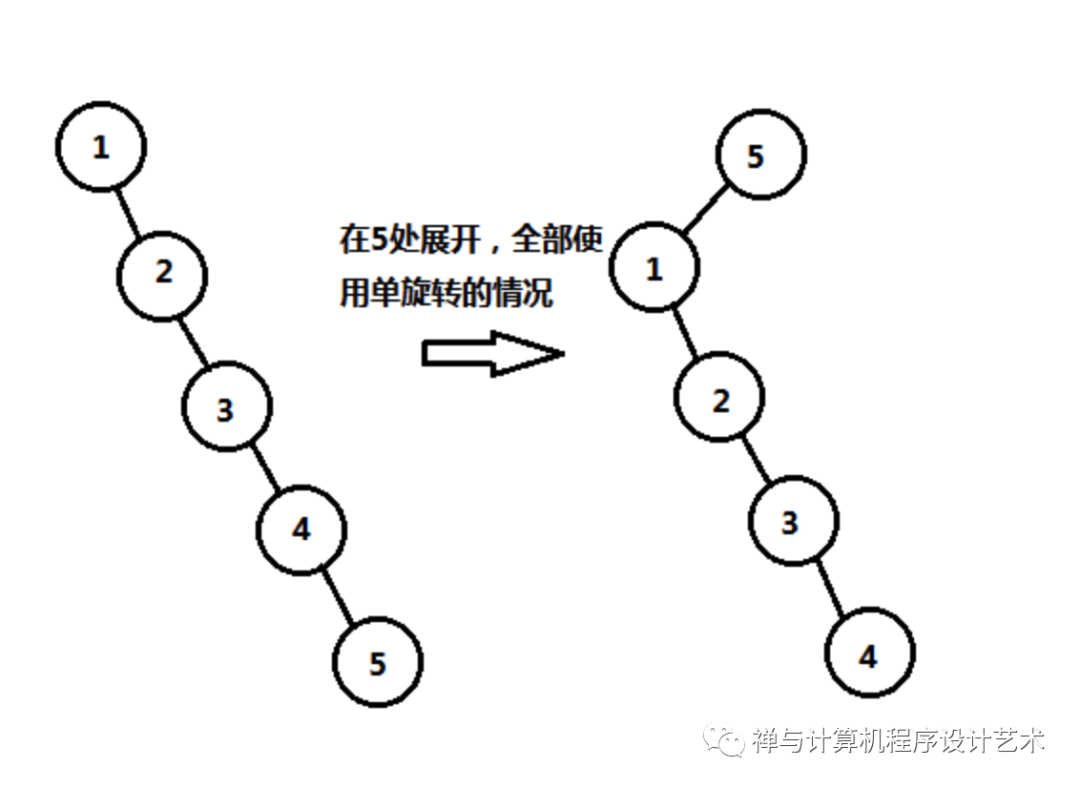
为了解决这个问题，我们采取一种特别的实现，根据三种情况进行旋转：

（1）当前结点只有父亲结点，使用单旋转，很明显这种情况的父亲结点为根结点；

（2）当前结点有父亲结点和祖父结点，呈之字形，例如当前结点是父亲结点的右儿子，父亲结点是祖父结点的左儿子。之字形的情况进行一次AVL双旋转，如下图：

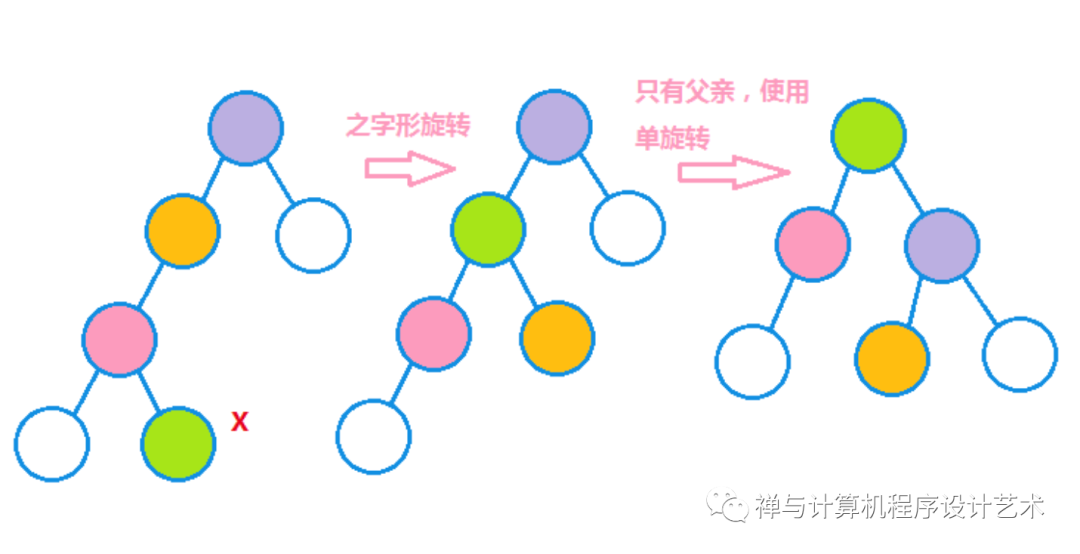
（3）当前结点有父亲结点和祖父结点，呈一字形，也就是类似LL和RR的情况，但是并不是使用单旋转，而是进行一字形对称旋转。假设祖父结点是根结点，那么让当前结点X成为根结点，父亲结点称为X的右儿子，祖父结点成为父亲结点的右儿子，X的原右儿子成为父亲的左儿子，父亲结点的右儿子成为祖父结点的左儿子，下图是一个例子：

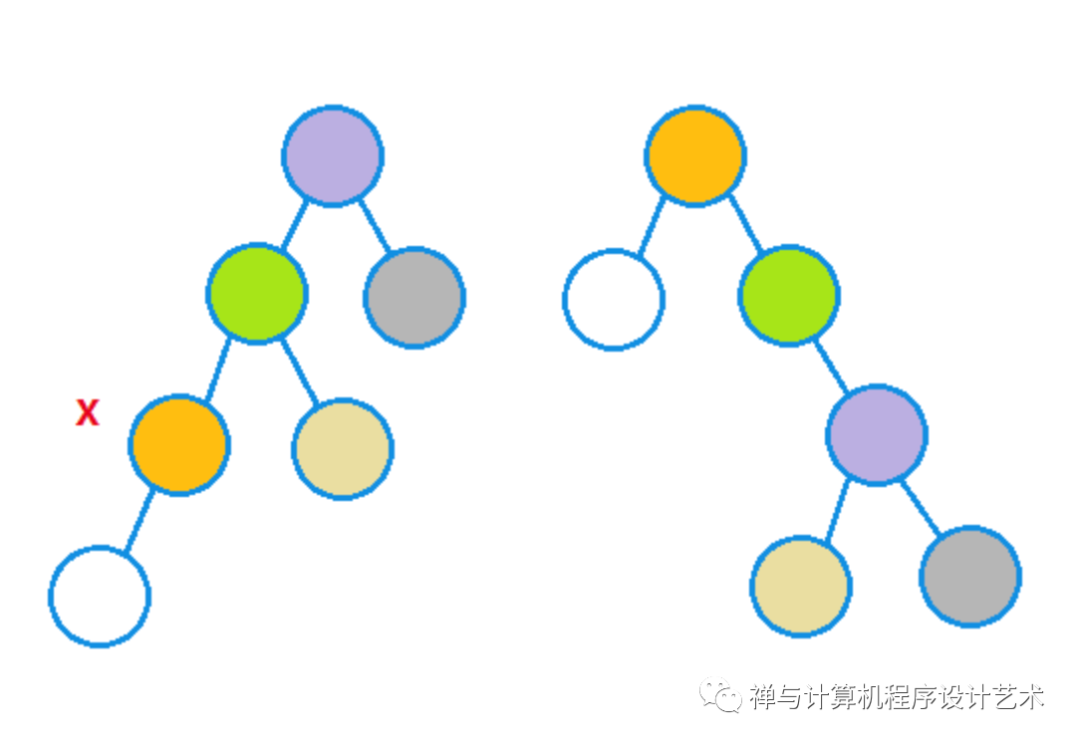
相对于仅仅使用单旋转，新实现方法的效率更高，使用新的旋转方式，对1、2、3、4、5的单链表情况在5处展开的过程如下图：

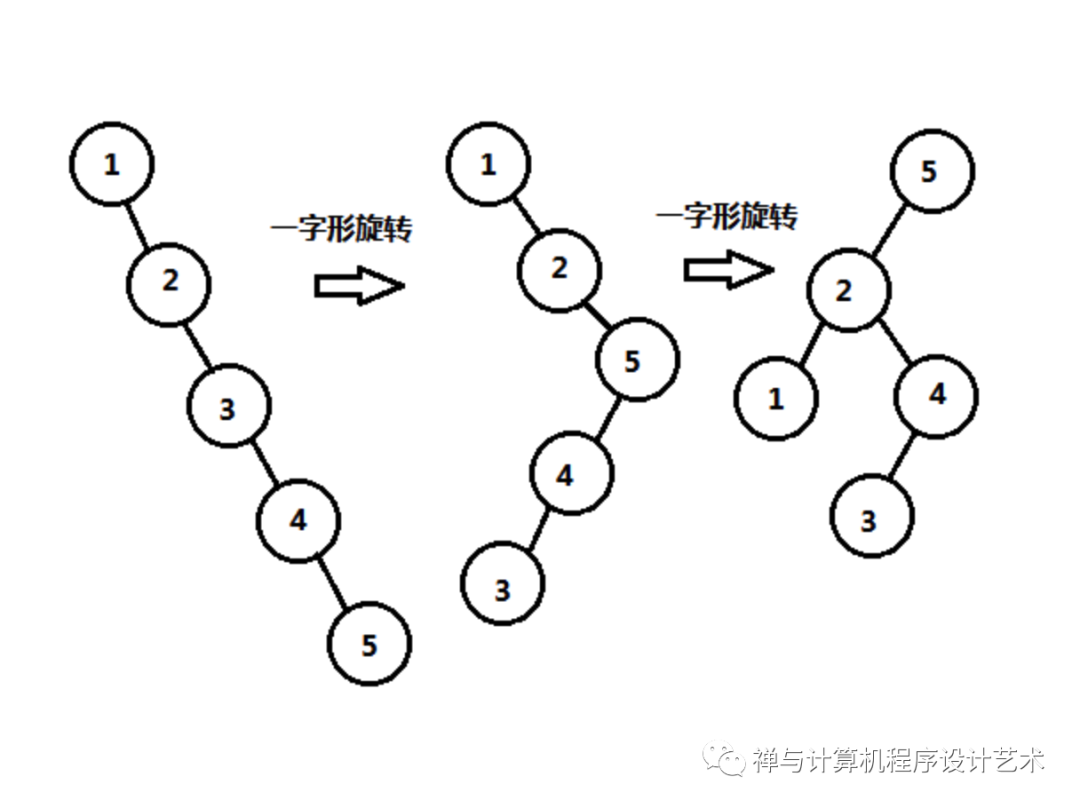
3、伸展树的数据结构和算法实现

伸展树的数据结构和普通二叉树的一样，至少提供指针域、数据域和关键字，而算法操作的实现稍微不同：

（1）对于增加、修改或查找结点数据，只要求将该目标结点上推到根结点；

（2）删除结点的操作为：将该删除的目标结点上推到根结点，删除根结点，此时分成了左右子树，接着找到左子树的最大结点，上推该结点为左子树的根，此时左子树没有右儿子，将右子树作为左子树的右儿子。

下面是伸展树ADT声明代码：

// 数据对象
typedef struct series{
    unsigned int id;
    char title[128];
    char introduction[256];
} Series;

// 结点
typedef struct splaynode{
    Series series;
    struct splaynode *left;
    struct splaynode *right;
} SplayNode;

// 伸展树ADT对外接口
typedef struct splaytree{
    SplayNode *root;
    unsigned int size;
} SplayTree;

// 算法声明
extern SplayTree *splaytree_init();
extern int splaytree_is_full(SplayTree *splaytree);
extern int splaytree_is_empty(SplayTree *splaytree);
extern int splaytree_add(SplayTree *splaytree, Series *series);
extern int splaytree_delete_by_id(SplayTree *splaytree, unsigned int id);
extern SplayNode *splaytree_get_by_id(SplayTree *splaytree, unsigned int id);
extern void splaytree_traverse(SplayTree *splaytree, void (*traverse)(SplayNode*));
extern int splaytree_clear(SplayTree *splaytree);

伸展树的重要操作是将目标结点提升为根结点，相对于AVL平衡树稍微简单，在删除数据上也比普通二叉树的删除操作简单，旋转是树的最基本操作，因此保证能掌握好旋转操作，结合普通二叉树的算法操作，旋转操作只是在每个结点上进行检查以进行旋转，该伸展树完整源码可查考github项目地址：https://github.com/onnple/splaystree，下图是该项目初始化的树结构：

六、B-树（B-Tree）

1、B-树的基本概念

B-树和下面的B+树是相当有用和比较重要的树数据结构（B-树和B树的叫法是一样的），应用于涉及硬盘数据的大量数据查找操作的场景。B-树也是一种平衡树，称为M路平衡查找树，M=2就是平衡二叉查找树，M称为阶数或度数或叉数或最多子树数，指的是一个结点拥有最多的儿子数。上面一直提到关键字域，关键字用于确定结点的分布规则，又称为键值，和数据库表的主键和唯一键是一样的。1个关键字最多有2个儿子，如二叉树，M阶平衡树的关键字数为M-1，在B-树的数据结构实现上，主要是使用关键字数M-1，可使用数组存储，或设计其它的容器如链式数据结构，其中3阶B树又叫2-3树，4阶B树又叫2-3-4树，如下图是一个3阶B叉树：

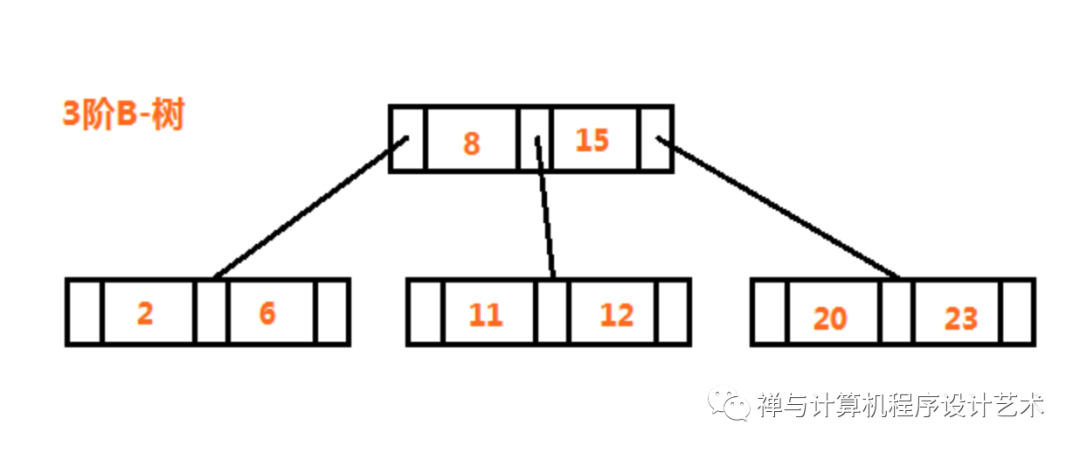
B-树的主要特性如下：

（1）每个结点的儿子数为2~M，为什么不是至少1个？因为B树的生长方向是自底向上，在分裂的时候不会造成只有1个儿子，为什么最大为M？因为阶数为M为最大儿子数，其关键字数最大为M-1；

（2）非根非叶子结点的儿子数为[M/2]~M，[]为向上取整，或使用ceil()函数，这个不用太注意，实际上只要你正确操作B树不会发生异常的情况；

（3）所有树叶的深度都相同，这就是说B树总是平衡的。

首先要指出，以上B-树只是一个参考的规范并不是绝对标准，你可以根据自己的需求自己设计，这里的M一直指的都是每个结点的最大儿子数，而在我们的代码中更直接的是使用关键字数，关键字数等于M-1，要注意是否混淆了。

B树的主要数据存储在所有结点上，和一般的二叉树是一样的，在二叉树上一个关键字对应一个数据对象，B树中H个关键字对应有H个数据对象，也就是说关键字和数据对象的数量是相同的。如果使用的是数据对象中的成员作为数据关键字，则在节点中可以直接声明一个数据对象的数组存储（或者其它类型的容器），否则自定义创建一个关键字数组，另外再创建数据对象数组，这样会相当麻烦（实际可以在数据对象中创建虚拟关键字，在结点声明）。

数据库索引：这里简单介绍一下数据库索引的概念，何为索引？关键字的集合就是索引了，实际上在线性表中的关键字也可以统称索引，但是我们说索引一般是和“高速“相关的，二叉树的所有关键字就是高速索引的例子，平衡树二叉树最坏情况也是O(logN)，索引可以使用数字或字符串，这个上面已经说过了，这个和MySQL等数据库中的概念是一样的。

和索引对应的就是数据对象或数据对象的地址，都是和关键字保存在一个结点中，这样如果一个结点过大，那么进行查找时IO操作次数就会多，例如一次IO最大访问数据量为Q，包含10个结点，如果没查找继续读取，但是如果一次把索引读出找到结点，再读取结点，这样两步就完成，后面介绍的B+树就可以实现这样的操作。

B树的最大深度为[log N]，底数为M/2，最坏运行时间为O(M logN)，底数为M，M为阶数，一般来说M=3或4时最好，当需要存储大量数据时，M可取值范围为：32<=M<=256，在结点上使用二分法查找时间为O(log M)，查找结点时间为O(logN)，其中M的选择应尽可能至少使得一个内部结点能装进一个磁盘块的最大值，假如一个结点大小大于磁盘块而加入一次IO只读取一个磁盘块，那么读取一个结点就要进行两次IO操作，相对于磁盘来说IO操作是一种实际的机械运动。

2、B-树的数据结构和算法设计

（1）B-树数据结构

B树的数据结构设计中，一般包含数据域，可存储实际的数据对象或数据对象的地址，关键字域，指针域，详细的结点信息包括：

父亲结点指针，方便在进行结点分裂或合并时操作；

关键字数量和关键字集，关键字使用升序排列；

儿子结点集，儿子结点的数量最大为M；

另外可选的信息包括：是否为叶子结点，数据域在数据库中存储的是数据的逻辑地址，在数据库中，一行称为一条记录（Record），一条记录包括了关键字（主键），数据域（其它字段数据），又可看作键值对。

数组长度可全部设定为M，对于关键字数组，多出一个位置可用于存储产生分裂的中结点，这里也可以将关键字和结点的左指针存储在数据对象中。

（2）B-树算法操作

B-树的操作算法中的难点也是插入和删除操作，下面先介绍B-树的插入操作：

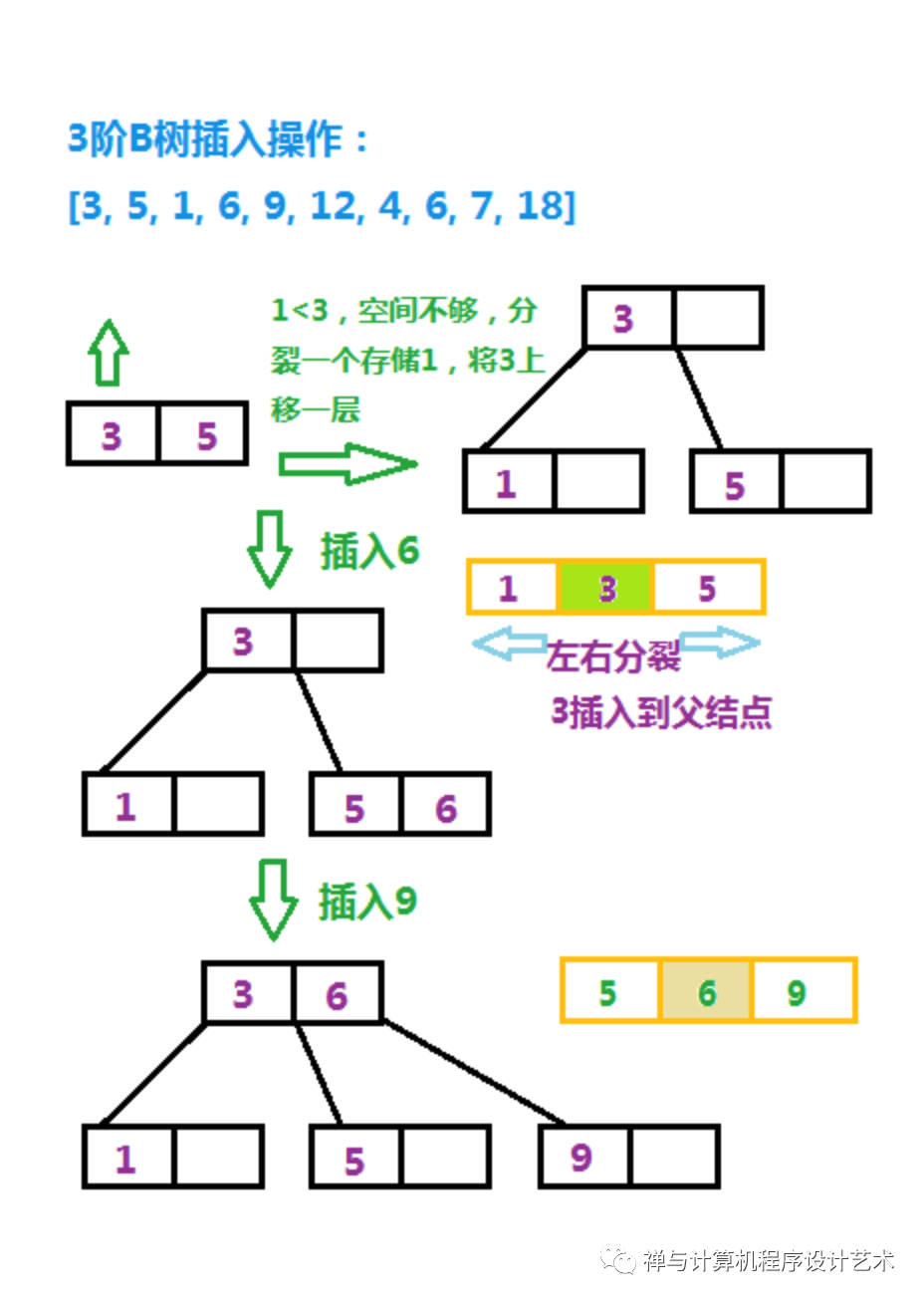
插入操作实际也并不是很难，就像上面的表达式树一样，描述起来可能有些复杂，但实现上并不复杂，插入过程如下：

设关键字数为K，关键字数组的大小为M，若K < M-1，即当前结点关键字数K小于最大的关键字数，则直接插入，一般插入需要重新排列；

若K == M-1，插入到关键字数组，此时数组大小为M，以第[M/2]个关键字为中心，将关键字数组分成左右两部分，即左右分裂成两个结点；

此时将第[M/2]个关键字插入到父结点，若当前结点没有父结点，则新建一个作为父结点，第[M/2]个关键字的左右儿子为分裂出来的左右两个结点。

其中有一个优化的方式是：按需插入数据，只要有合适的位置即插入，如上面的图片中9可以直接插入到3后面，此时就需要检查儿子结点的关键字数是否已满。

B-树删除操作：

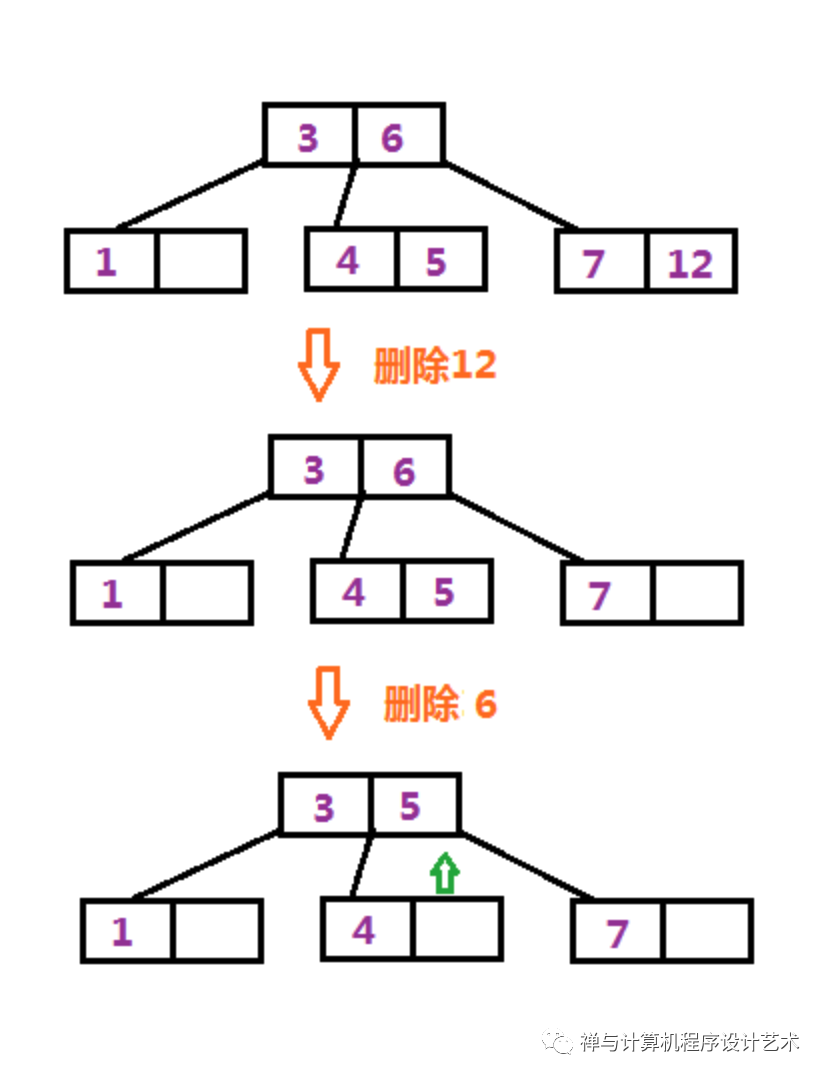
删除索引结点（内部结点）：使用右子树中最小的关键字进行覆盖（或左子树最大的关键字），再删除子树中的关键字，递归检查叶子结点。

删除叶子结点：没找到对应关键字结束删除，若找到则删除，设Q=[M/2]-1，若当前结点关键字数K>=Q，结束删除；

若K<Q，访问附近的兄弟结点，若兄弟结点的关键字数k>=Q，从兄弟借一个关键字：父结点关键字下移到当前结点，兄弟结点上移成为父结点，结束删除；若兄弟结点k<Q，将当前结点、父结点和兄弟结点合并。

综上，B-树插入数据空间满则分裂，删除数据不够则借或合并兄弟结点。

3、B-树数据结构和算法源码具体实现

B-树相对于普通的二叉树实现比较复杂，只要理解好，那么树这个数据结构就能掌握好了，树是难点而且也是相对有用的，先看下面的B-树ADT声明代码：

// 阶数或度数
#define DEGREE 3

// 数据表的一行记录，业务数据
typedef struct post{
    unsigned int id; // 关键字
    char title[128];
    char content[256];
} Post;

// B树结点，DEGREE阶B树，DEGREE-1个关键字，DEGREE个儿子，关键字使用多一个位置用于保存溢出的关键字
typedef struct bnode{
    unsigned int leaf; // 是否是叶子
    unsigned int size; // 关键字数量/记录数量
//    int keys[M_MAX]; // 关键字域，这里使用数据记录中的关键字，这样会比较好操作
    Post *posts[DEGREE]; // 数据记录集(Records)，B树的主要特点是数据记录存储在所有结点
    struct bnode *children[DEGREE]; // 儿子结点集
    struct bnode *parent; // 父结点
} BNode;

// 查找结果集
typedef struct resultset{
    unsigned int size;
    unsigned int id;
    Post *posts[]; // 结果记录
} ResultSet;

// B树ADT对外接口
typedef struct btree{
    BNode *root;
    unsigned int size;
} BTree;

// 算法声明
extern BTree *btree_init();
extern int btree_is_full(BTree *btree);
extern int btree_is_empty(BTree *btree);
extern int btree_add(BTree *btree, Post *post);
extern int btree_delete_by_id(BTree *btree, unsigned int id);
extern Post *btree_get_by_id(BTree *btree, unsigned int id);
extern void btree_traverse(BTree *btree, void(*traverse)(Post*));
extern int btree_clear(BTree *btree);

以上实现B-树的完整源码可到github上查看https://github.com/onnple/b-tree，该项目删除元素时是有些问题的，如发现望指正，另外，该项目值得参考，但是实现效果并不是很好，下面介绍B+树的内容，和B树是相似的，相关实现源码留待下一节提供。

七、B+树（B+Tree）

B树和B+树的主要应用在于数据库开发，例如MySQL的索引引擎就是使用B+树实现的，如此看来，使用数据库的目的除了数据持久化就是索引了，如果数据库失去了索引功能，那么和一般的文件访问也就区别不大了。说到数据库，这里稍微讨论一下相关的内容，数据库文件是存储在硬盘上的，程序访问数据需要调用外设硬件去读取硬盘上的数据，一次读取操作称为一次IO操作，IO操作是比较耗时的，因此提高数据访问的速度也就是要降低IO操作的次数。

相对于物理磁盘而言，数据的最小单位为扇区，一般512字节，相对文件系统而言，一次IO操作读取的数据大小目前可达到4K，也就是8个扇区。假如一个结点为4K，N个结点，最多深度为O(log N)，底数为M/2，加入一个结点存储200个关键字，一百万个结点只需读取几次即可，而关键字的查询速度也是对数时间O(log M)，如此你可以发现使用B树或B+树的功能强大。

1、B+树基本概念

B+树和B树的定义是等价的，其中有的定义是儿子数比关键字数小1，这个不是很重要，完全可以自定义。和B树不同的是B+树主要分为索引结点和叶子结点，索引结点为内部结点，主要用于存储关键字，不再存储数据，这样一个索引结点的空间就小多了（一次IO操作可以读取更多的关键字），叶子节点是数据记录存储的地方。索引结点中的关键字按升序排列。另外和B树主要不同的是，B+树每个叶子结点保存相邻叶子结点的指针（双向链表），这样因为叶子结点中的关键字也是按升序排列的，那么B+树不仅可以提供随机访问，还可以进行范围访问，因此使用B+树实现索引引擎会比B树更有优势。

注意，只有叶子结点才存储实际数据，MySQL的InnoDB引擎直接在叶子结点存储数据本身，而MyISAM引擎则是在叶子结点存储数据的逻辑地址，前者的方式称为聚簇索引，后者称为非聚簇索引，下面是这两种索引结构的粗略图：

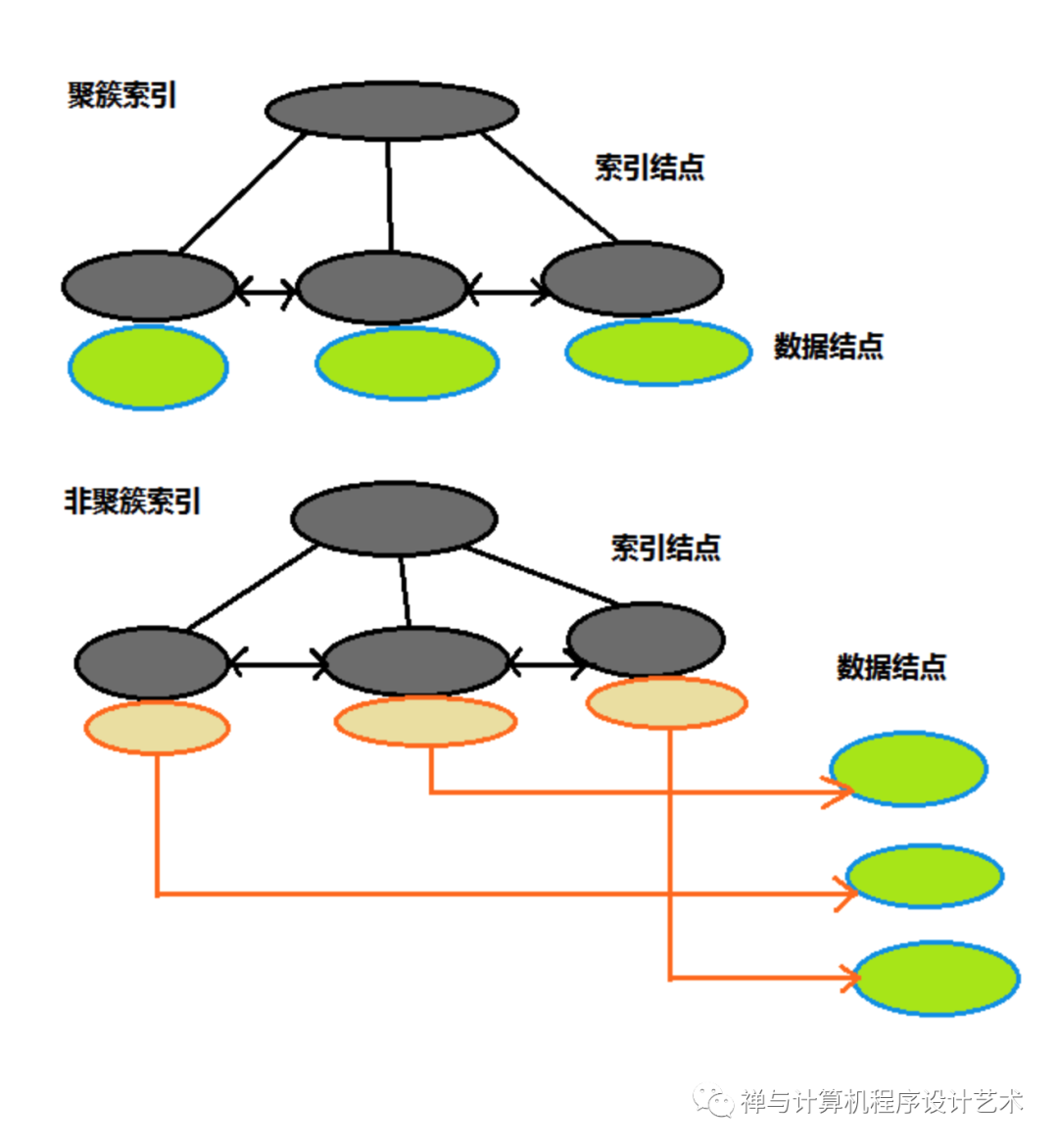
2、B+树的插入操作和删除操作

（1）B+树插入操作

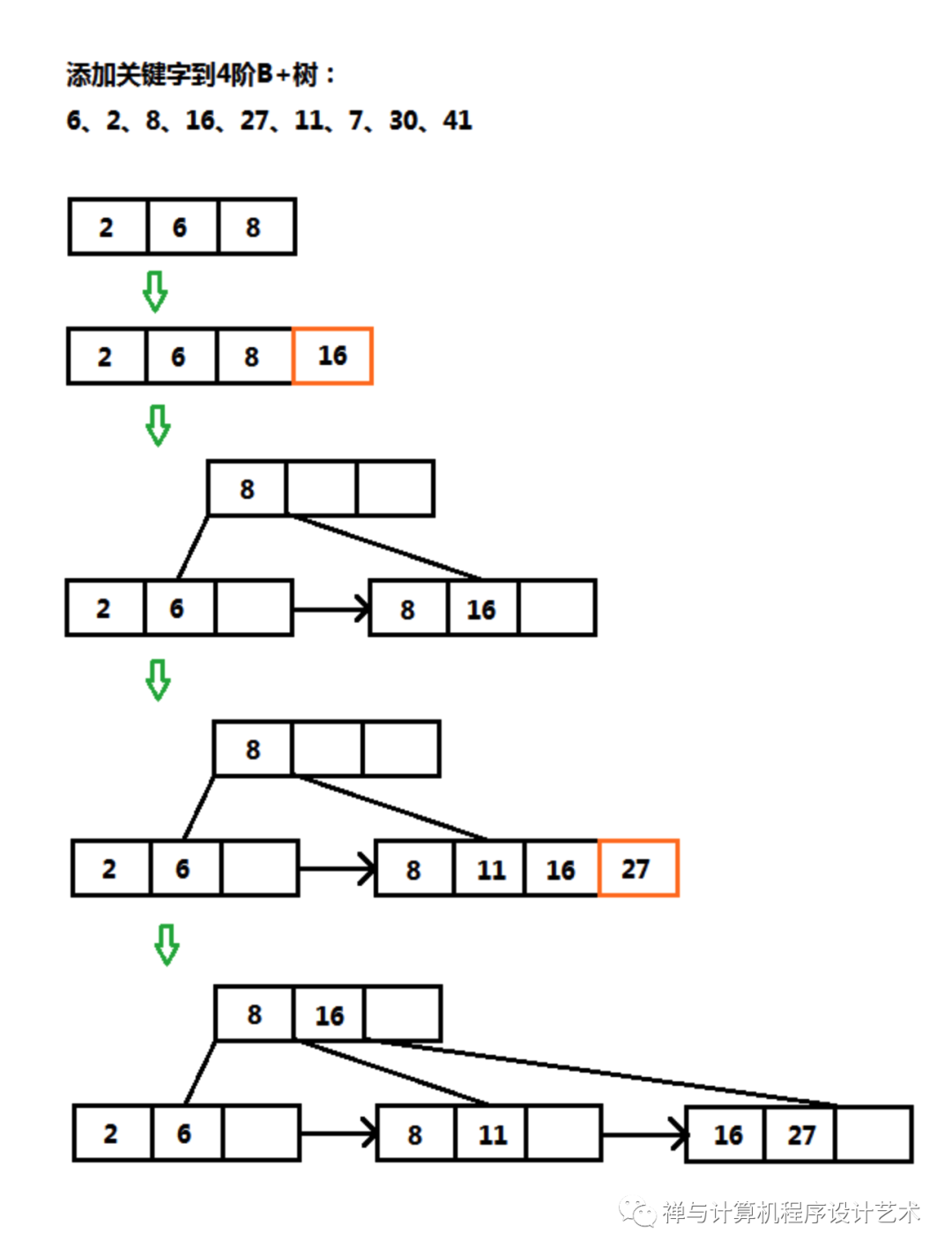
空树或结点未满，直接插入；

对于索引结点，先插入关键字到结点中，关键字树为K：

K <= M-1，插入结束；

K > M-1，分裂结点，分成左右两个结点，以[M/2]个关键字为中心，该结点进入父结点，中心关键字分到右边，右边部分的中心关键字不去除（非叶子结点在右边部分则不保留中心关键字）。

对于叶子结点，先插入关键字到结点中，K <= M-1，插入结束；

K > M-1，分裂结点，分成左右两部分，以第[M/2]个关键字为中心（非叶子结点不保留中心关键字）。

以上操作均为递归操作，往父结点添加关键字同样需要重新检查K的大小。

（2）B+树删除操作

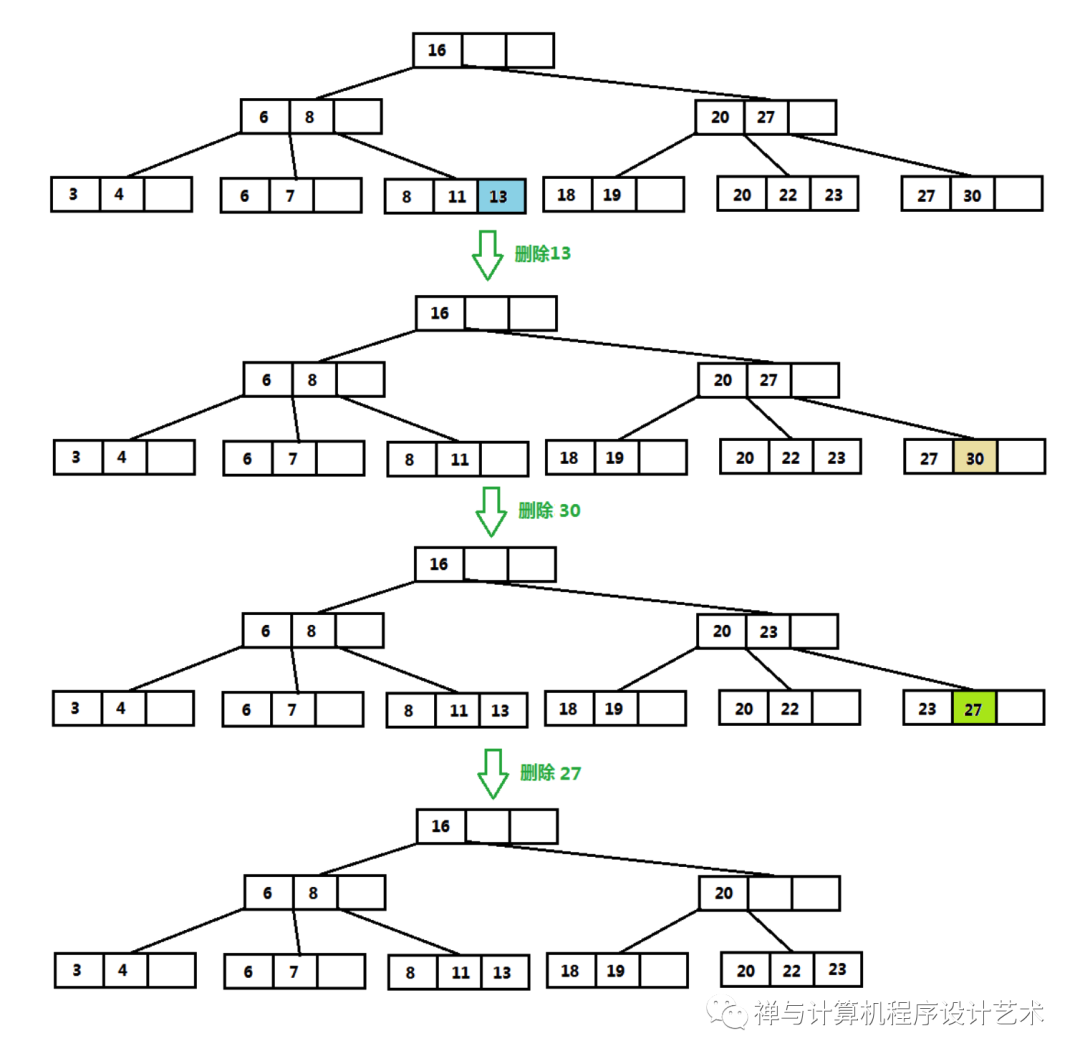
设Q=[M/2]-1，对于叶子结点：

没有对应的关键字，结束删除；

有对应关键字，关键数K >=Q，结束删除；

K < Q，检查兄弟结点的关键字k，k>Q，借兄弟结点的关键字；k<=Q，合并当前结点、父亲结点和兄弟结点的关键字。

B树的数据结构和算法详解

1、B树的基本定义

在上一节我们是使用最大度数或阶数M来定义B树的，这种一般的定义方式如下：

根结点度数M>=2；
叶子结点的深度相同；
非叶结点的度数：[M/2] <= T <= M，[]为向上取整符号；
结点的关键字数：[M/2]-1 <= K <= M-1；
关键字数K和结点度数T的关系为：K=T-1。

以上定义是正确的，但是问题是M如果为奇数在处理插入和删除的时候会有问题，这时候关键字数就为偶数，分裂结点就没那么方便了。

另一种B树的定义是使用最小度数t进行定义，该方式也是算法导论中采取的方式：

最小度数t>=2，B树的最小度数与磁盘块的大小有关；
根结点的关键字数最小为1；
叶子结点的深度相同；
非叶非根结点的度数：t <= T <= 2t；
非根结点的关键字数：t-1 <= K <= 2t-1；

（6）关键数K和度数的关系为：K = T – 1。

之后你会发现使用最小度数实现B树会更加优雅，B树每个结点的关键字都按升序排列。设B树的关键字数为N，则B树的关键字数N >= 2t^h-1，h为B树的高度h <= log((N+1)/2)，底数为t，t>=2，B树的所有一般操作的时间复杂度为O(log N)，底数为t。

2、B树的数据结构

B树的结点至少包括：

键值数组或关键字数组，长度为2t-1，长度为2t-1时结点为满；
最小度数t，最大度数为2t；
儿子指针数组，长度为2t；
当前关键字数目n，最大值为2t-1；
是否是叶子，用于标识一个结点是否是叶子结点，叶子结点没有儿子或其儿子为空。

下面是B树数据结构和算法声明的代码：

//
// Created by Once on 2019/7/22.
//

#ifndef TREE_BTREE_H
#define TREE_BTREE_H

// 键值数组结构
typedef struct column{
    int id; // 关键字
    char title[128];
} Column;

// B树结点
typedef struct bnode{
    int size; // 当前关键字数目
    Column **columns; // 键值数组
    struct bnode **children; // 儿子指针数组
    unsigned int leaf; // 是否为叶子
} BNode;

// B树ADT对外接口
typedef struct btree{
    unsigned int degree; // 最小度数
    BNode *root; // 根结点
    unsigned int size; // B树结点大小
} BTree;

// B树算法操作声明
extern BTree *btree_init(unsigned int degree);
extern int btree_is_full(BTree *btree);
extern int btree_is_empty(BTree *btree);
extern int btree_add(BTree *btree, Column *column);
extern int btree_delete_by_id(BTree *btree, int id);
extern Column *btree_get_by_id(BTree *btree, int id);
extern void btree_traverse(BTree *btree, void(*traverse)(Column*));
extern int btree_clear(BTree *btree);

#endif //TREE_BTREE_H

3、创建B树

C语言使用malloc创建一个B树，可预先创建一个根结点，也可以在插入数据的时候创建，初始化数据结构中的基本值，包括当前关键字数，是否是叶子，在处理B树持久化的时候，需要将新的根结点写入硬盘。这里仅仅初始化B树，不预先创建根结点：

BTree *btree_init(unsigned int degree){
    BTree *btree = (BTree*)malloc(sizeof(BTree));
    if(!btree){
        perror("init b tree error.");
        return NULL;
    }
    btree->root = NULL;
    btree->size = 0;
    btree->degree = degree;
    return btree;
}

4、B树遍历算法

树的遍历原则是以一个关键字为中心，左右儿子为该关键字的上限和下限，在B树遍历中，需要遍历结点上的关键字，在这里可使用while或for循环顺序遍历，时间为O(t)，也可以使用二分法遍历，时间为O(log t)，顺序遍历一个B树的描述如下，这是一个中序遍历：

使用for循环，上限为当前结点关键字数size，索引为i；
先遍历第i个非叶子儿子，此时即递归自身；
处理第i个关键字；
后处理第i+1个儿子，递归自身；
处理第i+1个关键字；
以上操作循环处理，跳出循环后需要处理最后一个儿子。

B树遍历算法代码如下：

static void traverse_tree(BNode *root, void(*traverse)(Column*)){
    int i;
    for (i = 0; i < root->size; ++i) {
        if(!root->leaf)
            traverse_tree(root->children[i], traverse);
        traverse(root->columns[i]);
    }
    if(!root->leaf)
        traverse_tree(root->children[i], traverse);
}

void btree_traverse(BTree *btree, void(*traverse)(Column*)){
    if(btree == NULL || btree->size == 0)
        return;
    traverse_tree(btree->root, traverse);
}

5、B树搜索算法

B树的搜索算法输入参数为B树的根结点root和待查找的关键字k，输出为NULL，找到对应的关键字则返回目标结点以及目标关键字的索引位置，这里实现仅仅返回关键字对应的值。

B树搜索的重点在于确定关键字的位置，包括确定相等关键字的位置，同时确定下层儿子的位置，这里要说一下关键字的索引和儿子的索引的关系，如下图：

结点上确定关键字位置的算法有两种，线性搜索和二分法搜索，线性搜索的时间为O(t)，此时B树的总时间为O(t log N)，底数为t，二分法搜索的时间为O(log t)，此时B树的总时间为O(log t log N))，B树搜索算法代码如下：

// 顺序查找结点关键字，每个结点最多关键字为2t-1，时间复杂度为O(2t-1)，即O(t)
static int seq_search(const Column *array[], const int len, const int value){
    int i = 0;
    while(i <= len - 1 && value > array[i]->id)
        i++;
    return i;
}

// 二分法查找结点上相同的关键字、确定儿子访问位置，每个结点关键字数为2t-1，时间复杂度为O(log(2t-1))，即O(log t)
static int binary_search(Column *array[], const int len, const int value){
    int start = 0, end = len - 1, index = 0, center = (start + end) / 2;
    while(start <= end){
        if(value == array[center]->id){
            index = center;
            break;
        }
        else if(value > array[center]->id){
            index = center + 1;
            center += 1;
            start = center;
        }
        else{
            index = center;
            center -= 1;
            end = center;
        }
        center = (start + end) / 2;
    }
    return index;
}

static Column *btree_get(BNode *root, int id){
    int index = binary_search(root->columns, root->size, id);
    if(index < root->size &&  root->columns[index]->id == id)
        return root->columns[index];
    else if(root->leaf)
        return NULL;
    else
        return btree_get(root->children[index], id);
}

Column *btree_get_by_id(BTree *btree, int id){
    if(btree == NULL || btree->size == 0)
        return NULL;
    return btree_get(btree->root, id);
}

6、B树插入算法

B树的插入最主要就是结点分裂了，一般来说如果一个结点满了，则分裂成两个结点，中间的关键字插入到父结点，这样向上分裂，但是关键字是插入到叶子结点的，等到插入关键字再分裂结点，则处理会比较麻烦。

这里B树插入采用另一种方式：插入关键字从根结点自上而下查找关键字所属位置，将关键字添加到叶子结点上；沿途经过的结点若满（满的关键字数为2t-1）则分裂结点，以第(t-1)个关键字为分界点，分成两个结点，每个结点的关键字数为t-1，将第t-1个关键字插入到父结点，这样将关键字插入到叶子结点时就不需要再分裂，如下图，插入6之前先将根结点分裂，然后再从根结点上获取新的路径插入到叶子结点上。

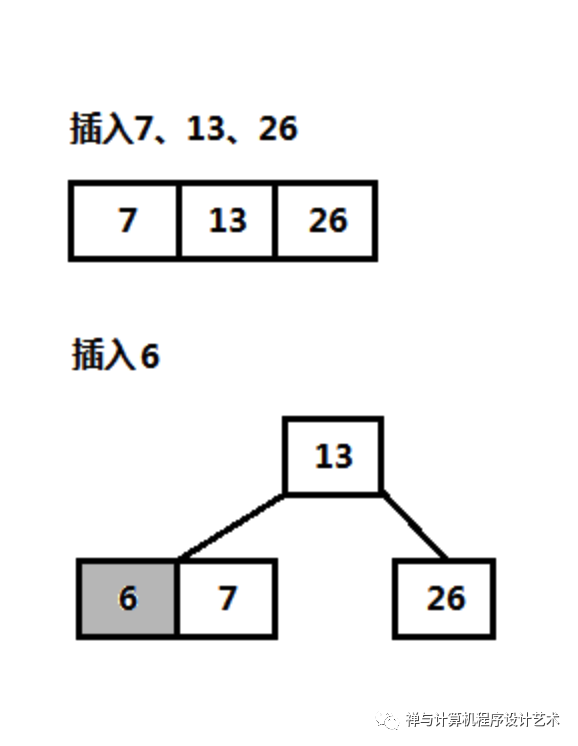
B树插入算法的大体流程如下图所示，其总体流程包括满结点分裂、非满结点插入：

取出根结点，如果根结点已满则分裂该结点，然后更新根结点，向下选择路径，检查途径的结点，如果是内部结点，检查该结点的儿子结点是否已满，若满则分裂，否则继续向下，如果是叶结点则插入关键字，插入结束。

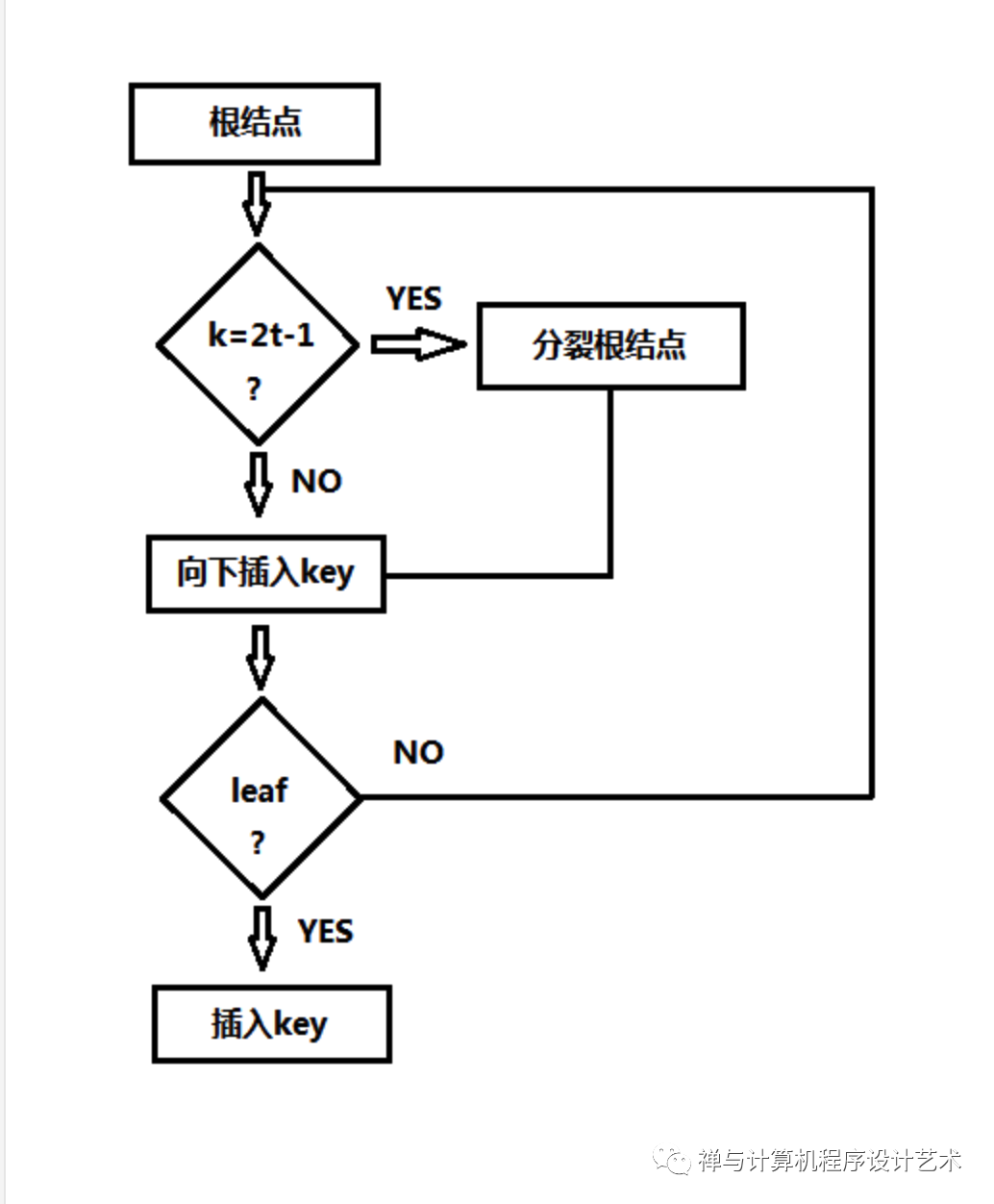
（1）分裂结点算法

分裂结点分裂的不是当前结点，而是当前结点的儿子结点，分裂结点算法的输入参数包含儿子为满的父结点，以及满儿子在父结点中的索引位置i，这个i在向下选择路径的时候可以求得到。

在自上而下查找关键字位置时，分裂途径的满结点，关键字数为2t-1为满，分裂的结点包括叶子结点，这样在分裂当前结点时，可保证它的父结点不是满的，也就是不需要再向上分裂了，分裂算法的详细描述如下：

以当前结点作为父结点，检查向下的儿子s结点是否已满，而根结点的分裂会导致创建新的根结点n；
如果根结点已满，则创建并初始化新结点n（包括当前关键字数、是否为叶结点），在节点s中将从第t个开始的关键字转移到n中，非叶结点需要从第t个开始转移儿子到n中；
将新结点添加到当前结点（父结点）作为儿子；
将第t-1个关键字添加到当前结点（父结点）中。

以上分裂算法都是针对当前结点分裂儿子结点，在路径每一个结点上都需要检查，若结点已满则调用该分裂算法，代码如下：

/**
 * 1、创建新结点n
 * 2、转移关键字到n
 * 3、转移儿子到n
 * 4、n添加作为parent的儿子
 * 5、将中间关键字添加到parent
 * */
static int split_child(BTree *btree, BNode *parent, int index){
    BNode *left = parent->children[index];
    BNode *right = (BNode*)malloc(sizeof(BNode));
    if(!right)
        return 0;
    right->columns = (Column**)malloc(sizeof(Column*) * (2 * btree->degree - 1));
    right->children = (BNode**)malloc(sizeof(BNode*) * (2 * btree->degree));
    if(!right->columns || !right->children)
        return 0;
    right->leaf = left->leaf;
    for (int i = btree->degree; i < left->size; ++i) {
        right->columns[i - btree->degree] = left->columns[i];
    }
    if(!left->leaf){
        for (int i = btree->degree; i < left->size + 1; ++i) {
            right->children[i - btree->degree] = left->children[i];
        }
    }
    right->size = btree->degree - 1;
    left->size = btree->degree - 1;
    for (int k = parent->size; k > index; --k) {
        parent->columns[k] = parent->columns[k - 1];
    }
    parent->columns[index] = left->columns[btree->degree - 1];
    for (int j = parent->size + 1; j > index + 1; --j) {
        parent->children[j] = parent->children[j - 1];
    }
    parent->children[index + 1] = right;
    parent->size++;
    return 1;
}

（2）B树插入关键字

完整的插入算法输入参数包括根结点和待插入的关键字，以上的分裂算法只处理满结点的情况，那么非满结点也需要做处理，下面是该算法的完整描述：

先检查B树的根结点，如果根结点为满，则创建一个新的根结点，调用分裂算法进行分裂，处理完成后再以新的根结点为起点调用非满插入算法；
关键字数小于2t-1为非满，如果当前结点为叶子结点，则将关键字插入到结点中；
如果当前结点为内部结点，获取下一个儿子结点，检查是否需要分裂，分裂完成后，再递归调用非满插入算法。

同样的，以上检查结点是否已满，除了根结点外，都是检查儿子结点的，下面是完整的关键字插入代码：

static int add_none_full(BTree *btree, BNode *root, Column *column){
    int index = binary_search(root->columns, root->size, column->id);
    if(root->leaf){
        if(index < root->size && root->columns[index]->id == column->id){
            strcpy(root->columns[index]->title, column->title);
            return 1;
        }
        Column *c = (Column*)malloc(sizeof(Column));
        if(!c)
            return 0;
        c->id = column->id;
        strcpy(c->title, column->title);
        for (int i = root->size; i > index; --i) {
            root->columns[i] = root->columns[i - 1];
        }
        root->columns[index] = c;
        root->size++;
        return 1;
    }
    else{
        if(root->children[index]->size == 2*btree->degree - 1){
            if(split_child(btree, root, index)){
                if(column->id > root->columns[index]->id)
                    index++;
            }
            else
                return 0;
        }
        return add_none_full(btree, root->children[index], column);
    }
}

static int add_node(BTree *btree, BNode *root, Column *column){
    if(!root){
        root = new_node(btree);
        if(!root)
            return 0;
        Column *c = (Column*)malloc(sizeof(Column));
        if(!c)
            return 0;
        c->id = column->id;
        strcpy(c->title, column->title);
        root->leaf = 1;
        root->columns[0] = c;
        root->size = 1;
        btree->root = root;
        btree->size++;
        return 1;
    }
    else{
        if(root->size == 2*btree->degree - 1){
            BNode *node = new_node(btree);
            if(!node)
                return 0;
            node->leaf = 0;
            node->size = 0;
            btree->root = node;
            node->children[0] = root;
            btree->size++;
            if(split_child(btree, node, 0)){
                int i = 0;
                if(node->columns[0]->id < column->id)
                    i++;
                return add_none_full(btree, node->children[i], column);
            }
            return 0;
        }
        else
            return add_none_full(btree, root, column);
    }
}

int btree_add(BTree *btree, Column *column){
    if(btree == NULL || column == NULL)
        return 0;
    return add_node(btree, btree->root, column);
}

7、B树删除算法

B树的删除操作比较复杂，下面我们来一步步分析，我们可以想到，删除的情况有两种：内部结点和叶子结点，这里删除的方式也是和插入类似，一次遍历完成删除操作，因为删除一个关键字可能会导致结点关键字不足t-1个，这就需要借或者合并相邻结点。

这里我们采取这样的方式，一般来说非根结点关键字数至少为t-1个（根结点至少为1个关键字），递归下降遍历，对每个沿途经过的结点，保证结点的关键字说为t（比最小关键字数t-1多1），儿子结点关键字不足t时，从父结点下移一个到儿子中，将兄弟结点的关键字上移一个到父结点，当前结点关键字为空，删除当前结点，让儿子成为新的根，这种方式保证内部结点的关键字数至少为t，这样从内部结点删除一个关键字时就不会导致该结点为空或少于t-1个关键字，下图是B树删除操作的大体流程，下面我们详细讨论操作流程：

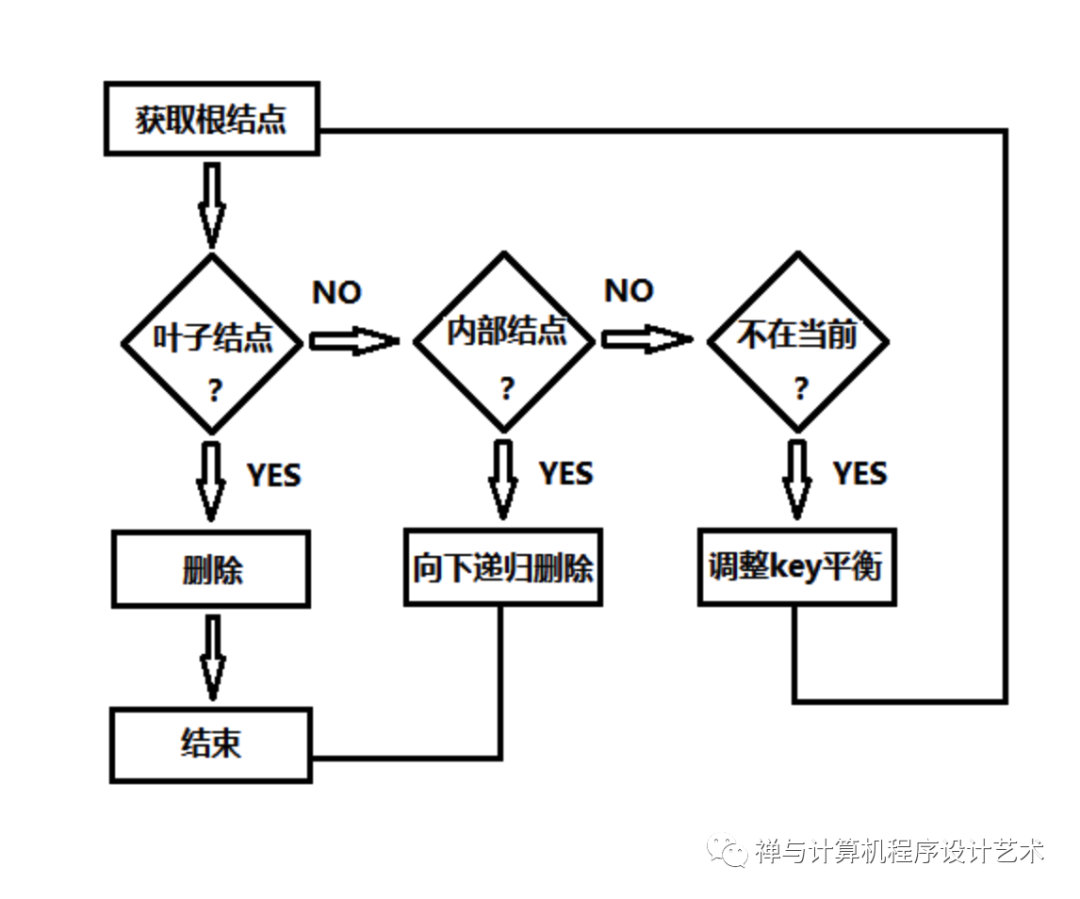
删除操作输入参数为根结点和待删除的关键字k，删除的操作分为以下三种情况：

k在叶结点中：直接删除关键字k，如果不存在也删除结束；
k在内部结点中：以当前待删除的关键字k为中心，k有左右儿子：
k的左儿子关键字数>=t，将左子树的最大值M替换k，递归向下删除M；
k的右儿子关键字数>=t（k的左儿子的关键字数<t），将右子树的最小值m替换k，递归向下删除m；
k的左右儿子关键字数==t-1，将k和左右儿子合并进左儿子，在当前结点中释放右儿子和k，从左儿子递归向下删除k。
k不在当前结点中：当前结点的向下儿子s，k有可能在以s为根的结点中，此时我们需要将s的关键字调整至少t个关键字，（向左借、向右借、合并左或右）调整的情况如下：
s结点只有t-1个关键字（相邻兄弟关键字>=t），将当前结点的一个关键字下移到s中，将左或右兄弟一个关键字上移到当前结点，将兄弟中关键字相应的儿子移到s结点中；
s结点和所有相邻兄弟结点都只有t-1个关键字，将s和其中一个兄弟合并，将当前结点的一个关键字移到新合并的结点中。

删除算法可分为：当前结点存在关键字，则删除叶子结点或者内部结点的关键字，不存在则需要检查儿子结点进行填满t个关键字的操作。B树的完整源码可在github上查看：https://github.com/onnple/B-TREE-C，该项目的删除操作有bug，但是由于时间问题就不再进行调试了，感兴趣的朋友可以指正一下。

二、B+树

B+是B树的扩展，它和B树在结构上主要的不同在于，B+树的所有叶结点是使用链表链接的，而且B+树的叶结点包含了全部的关键字，下面B+树图片取自于维基百科：

B+树的主要应用在操作系统的文件系统和数据库，这里就不实现B+树了，需要应用B+树的特性那么使用例如MySQL等数据库是最好的方式。

如果需要自定义实现B+树，B+树的数据结构和B树的基本一样，不过叶子结点需要增加左右兄弟的指针。B+树的算法操作也和B树基本一样，但是要注意因为B+树的所有叶子结点包含了所有的关键字，所以在插入操作分裂结点中，中间的关键字除了插入父结点，需要保留在叶子上，删除操作则需要把叶子上相同的关键字一并删除。

三、MySQL数据库索引引擎实现原理

如果你用过MySQL数据库的话，可能知道在MySQL存储数据有几种文件，例如.frm文件、.myi文件、.myd文件和.ibd文件，首先.frm文件是MySQL用于表示表结构的文件，一般创建一个新表都会创建这样的文件。

MySQL数据库有两大索引引擎：MyISAM引擎和InnoDB引擎，这两个索引引擎都是基于B+树实现的，对于MyISAM索引引擎，它是一个非聚簇索引，即在叶子结点上存储数据的地址，所以使用MyISAM索引存储的数据分为两个文件：.myi文件和.myd文件，这两个文件分别存储索引和真实数据。

而对于InnoDB引擎，它直接在叶结点存储数据本身，因此是聚簇索引，只使用一个文件存储索引和真实数据，该文件就是.ibd文件。

1、MySQL索引引擎实现原理

首先我们要清楚，实现MySQL索引引擎并不是直接存储一个B+树，甚至并不需要一个真正的B+树，实际存储的是一个结点的数据，一次IO读取一个结点，从这个结点找出下一个结点的位置再次调用IO读取，所以索引引擎是一个逻辑上的B+树。

为什么要使用B+树索引数据？主要还是因为速度的问题，我们的真实数据存储在磁盘上，一般在内存里面的操作都不算耗时，反而机械磁盘耗时会比较明显，因为磁盘读取有真实的机械性操作，影响磁盘读取速度的主要因素是：盘片的旋转和磁臂的移动。那么如何实现速度最大化呢？那就是B+树了，B+树读取海量的数据只需要O(log N)次操作，而且其底数t可以最大化，InnoDB是将根结点常驻内存，以一个结点为一个数据单位，一次IO读取一个结点，MySQL设置的一个数据页为16K。

为什么使用B+树而不是B树？要知道B+树的结点不存储任何真实数据，只存储索引数据，而B树是两者都存储，这样相同大小16K的一个结点，B+树存储的索引数据比B树的多很多，这意味着B树的IO操作次数会比B+树的多，所以使用B+树实现索引更有优势，另外一个原因是因为B+树的所有叶结点都是相连的，B+树可以很方便地进行顺序访问或范围性访问。

MySQL在索引引擎实现上并不是严格遵守B+树的定义，例如结点分裂，MySQL采取的原则是空间优先，只要结点空间足够就插入，尽量最大化利用空间。

2、InnoDB 存储引擎索引原理

（1）存储结构

A、表空间（table space）：一个存储文件的主题，由段组成；

B、段（segment）：由簇组成，可分为数据段、索引段和回滚段；

C、区/簇（extent）：由64个连续的页空间组成（64x16k），段的最小单位，它是一个连续分配的段空间；

D、页（page）：磁盘块的最小单元，16k大小，常见的页有数据页（B-tree Node page）、事务数据页（Transacation system page）、Undo页和系统页，又称为一个记录（page==record），一个页等于一个结点。

（2）数据存储原理

磁盘由盘面、磁头、磁道（Track）、柱面（Cylinder）和扇区（Sector）组成，盘面从上而下从0开始编号，磁头由上而下从0开始编号，磁道由外向内从0开始编号，磁道的一段圆弧叫做扇区，扇区从1开始编号，柱面编号和磁头是一样的。

磁盘的数据寻址有两种方式：逻辑地址和磁盘地址，逻辑地址则是编程代码中获取的数据地址，一般用十六进制表示，磁盘地址是数据的物理地址，一般使用一个三位码表示（柱面号，磁头号，扇区号）。

磁盘IO读写的速度影响因素包括磁盘存储介质和机械运动，上面对索引引擎的存储结构的设计，一个依据是计算机局部性原理，也就是说设计结点的大小需要考虑磁盘块的大小，计算机局部原理是说，当一个数据被使用到时，附近的数据也会被马上用到，程序运行所需数据通常比较集中，在附近柱面，或附近磁头，或附近的扇区，另外程序预读数据也可以提高IO效率，预读的数据长度为页的整数倍。

【更多阅读】