一：引入

前文所讲到的波士顿房价预测案例中，涉及到的仅仅是一个非常简单的神经网络，它只含有输入层和输出层
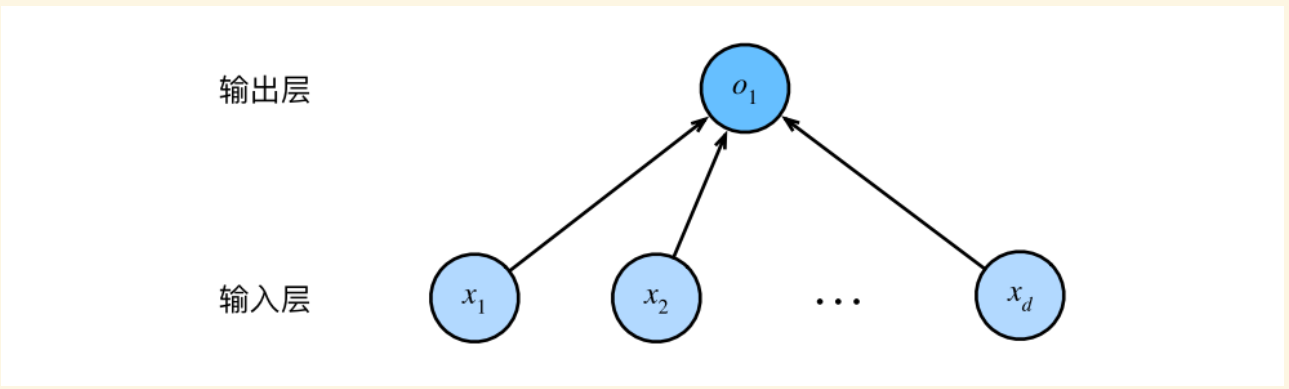
在这里插入图片描述

但观察最终结果，我们发现仅含有单个输出层的神经网络其预测效果并不是很好，甚至有些结果预测得都不合理

这是因为：简单的神经网络或简单的线性运算是存在很大问题的，任何特征的（微小）变化都可能导致模型最终输出发生巨大变化

那如何解决这个问题呢？我们的想法就是在输入层和输出层之间加入单个或多个隐藏层，并且这些隐藏层上的神经元并非像之前那样只做简单的线性运算，而是线性运算后再经过一个激活函数的作用，这样一来整个模型就具有了更好的非线性表达能力了。隐藏层有了，该如何连接呢？最简单的想法就是进行全连接，也即每一层神经元都接受上一层所有神经元的输入，然后输出给下一层的所有神经元，我们将这种结构称之为多层感知器（MLP）（又叫做人工神经网络）。如下图是一个仅包含单个隐藏层的MLP模型

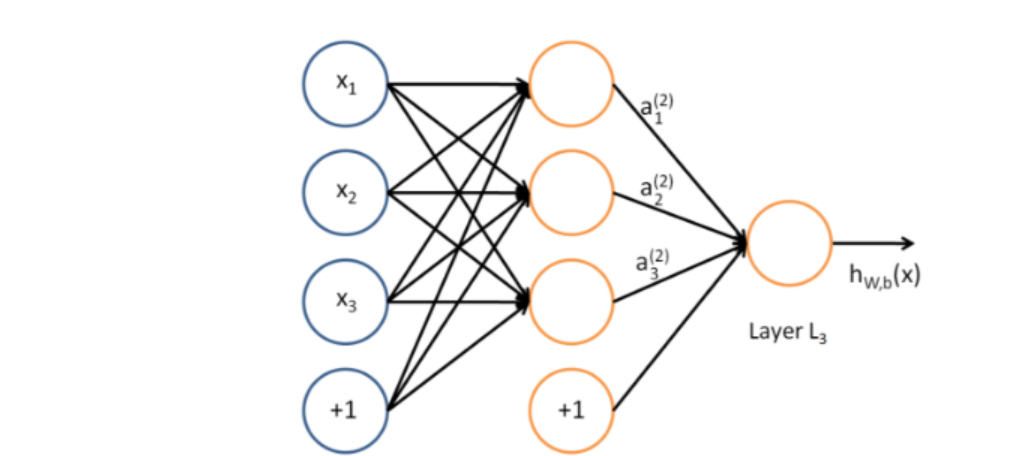
在这里插入图片描述

当然假如多个隐藏层时，这个神经网络的规模就很庞大了，此时称这种网络结构为全连接神经网络（DNN），在Pytorch中对应torch.nn.Linear

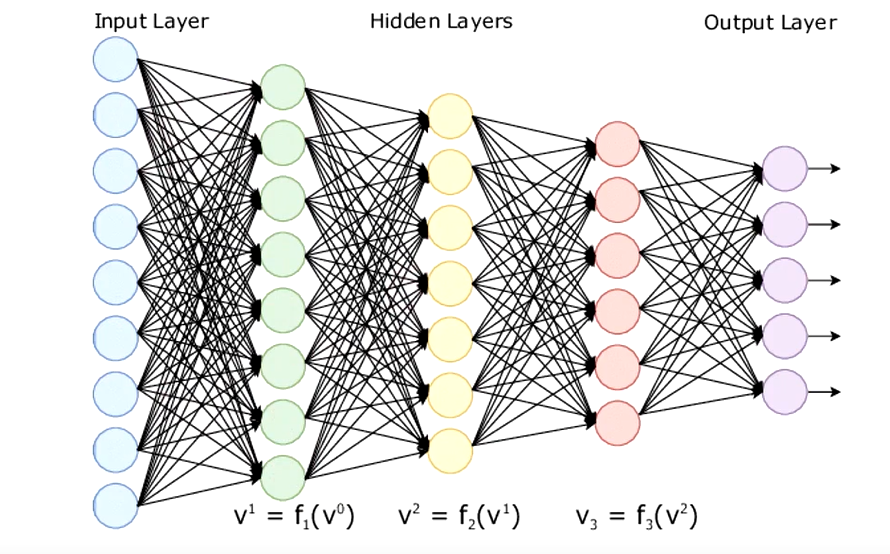
在这里插入图片描述

二：定义

多层感知器：多层感知器包含一个或多个在输入节点和输出节点之间的隐藏层，除了输入节点外，每个节点都是使用非线性激活函数的神经元。而在不同层之间，多层感知器具有全连接性，即任意层中的每个神经元都与它前一层中的所有神经元或者节点相连接，连接的强度由网络中的权重系数决定。多层感知器是一类前馈人工神经网络。网络中每一层神经元的输出都指向输出方向，也就是向前馈送到下一层，直到获得整个网络的输出为止

三：反向传播算法

“反向传播算法”过程及公式推导（超直观好懂的Backpropagation）

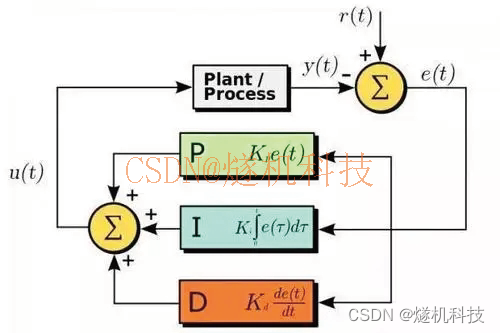
反向传播算法：多层感知器训练依托于反向传播算法，反向传播算法通过求解损失函数关于每个权重系数的偏导数（梯度），依次使误差最小化来训练整个网络

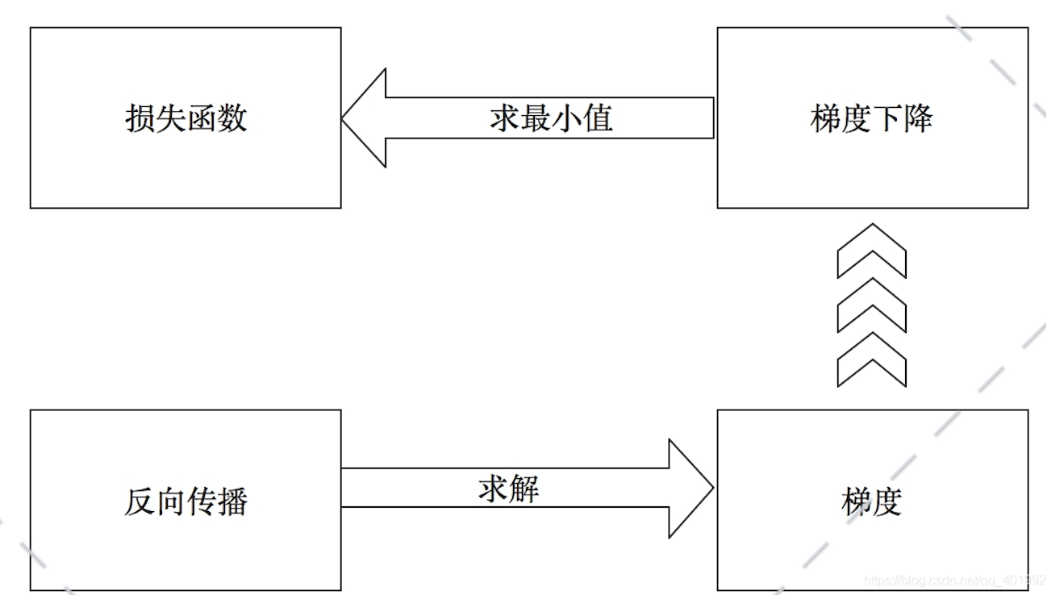
在这里插入图片描述

如下图
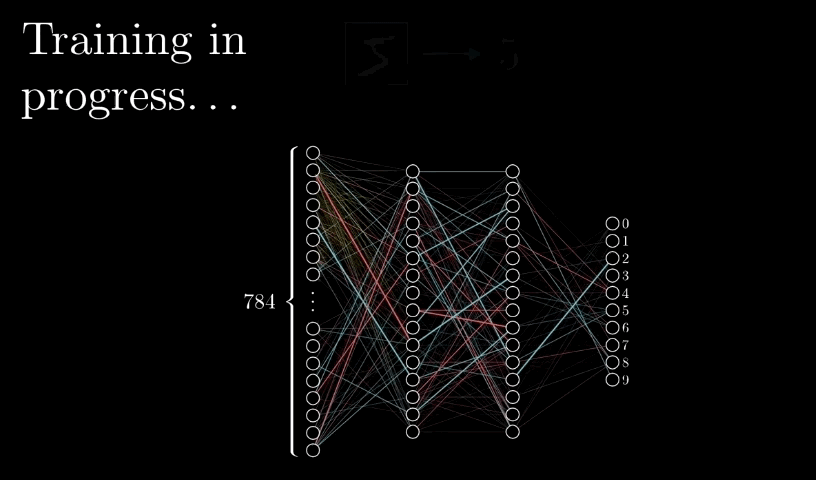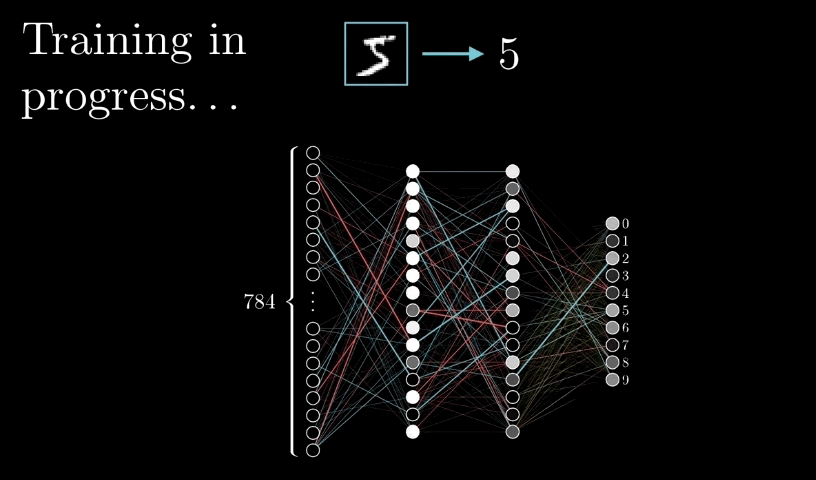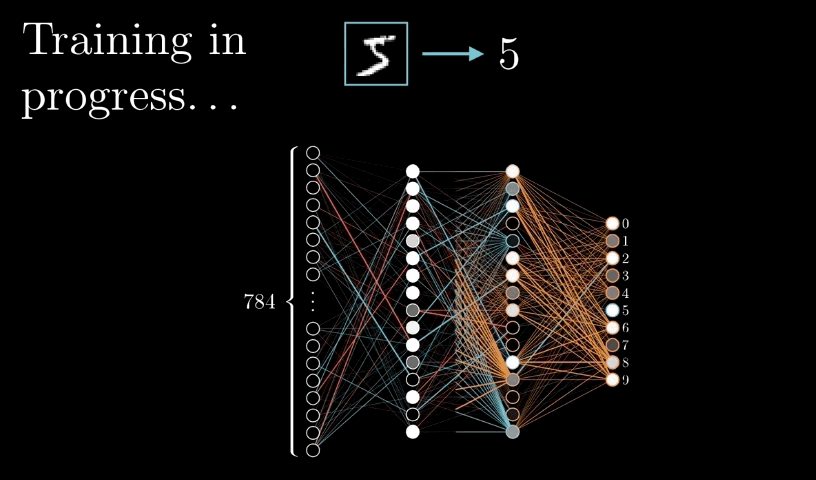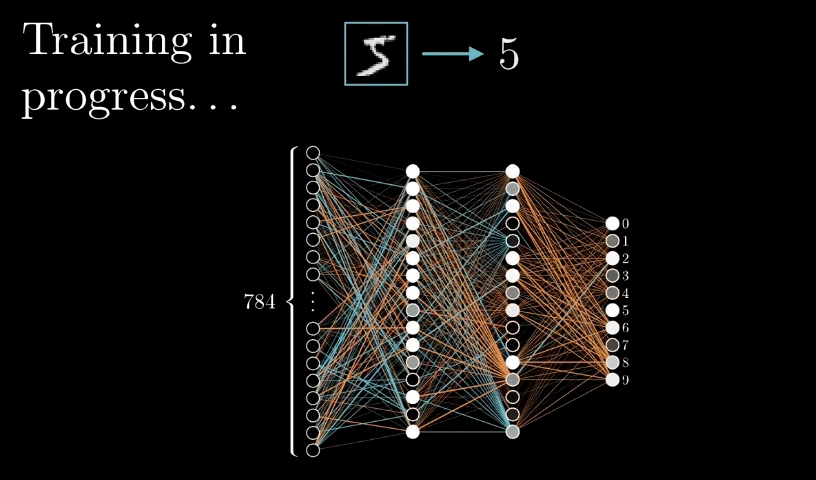
在这里插入图片描述

四：构建多层感知器完成波士顿房价预测

这里我们引入隐藏层构建一个简单的MLP来完成前文的波士顿房价预测

# 导包
import numpy as np
import torch
from sklearn.datasets import load_boston
import warnings
warnings.filterwarnings("ignore")

# 数据部分
# 读入数据
data = load_boston()
X = data.data
y = data.target

# 拆分数据
X_training = X[0:496, ]
y_training= y[0:496, ]
X_testing = X[496:, ]
y_testing= y[496:, ]

# 网路结构：这里加入一个隐藏层
class BostonPredictNet(torch.nn.Module):
    def __init__(self, n_feature, n_output):
            super(BostonPredictNet, self).__init__()
            self.hidden = torch.nn.Linear(n_feature, 100) # 隐藏层
            self.predict = torch.nn.Linear(100, n_output)
    def forward(self, x):
        out = self.hidden(x)
        out = torch.relu(out)  # 激活函数ReLU
        out = self.predict(out)
        return out

net = BostonPredictNet(13, 1) # 输入为13，输出为1
    
# 损失函数
loss_func = torch.nn.MSELoss()

# 优化器
optimizer = torch.optim.SGD(net.parameters(), lr=0.0001)

# 训练
for i in range(1, 10000):
    
    ###################### 训练 ###############################
    
    # 前向运算
    x_data = torch.tensor(X_training, dtype=torch.float32)
    y_data = torch.tensor(y_training, dtype=torch.float32)    
    pred = net.forward(x_data)
    pred = torch.squeeze(pred)  # 降维
    # 注意损失可能过大会导致无法显示所以可以先减小，但是注意最后要复原
    loss_train = loss_func(pred, y_data) * 0.01 # 计算损失

    
    # 反向传播（三步走）
    optimizer.zero_grad() # 初始化梯度为0，也即把损失函数关于权重系数的导数置为0
    loss_train.backward() # 计算梯度
    optimizer.step() # 梯度下降，更新参数
    print("-"*30)
    print("第{}次迭代".format(i))
    print("训练集loss为{}：".format(loss_train))
    print("（训练集）预测值：", pred[0:10])
    print("（训练集）真实值：", y_data[0:10])
    
    ###################### 测试 ###############################
    x_data = torch.tensor(X_testing, dtype=torch.float32)
    y_data = torch.tensor(y_testing, dtype=torch.float32)    
    pred = net.forward(x_data)
    pred = torch.squeeze(pred)
    loss_test = loss_func(pred, y_data) * 0.001 
    
    print("测试集loss为{}：".format(loss_test))
    print("（测试集）预测值：", pred)
    print("（测试集）真实值：", y_data)