738.单调递增的数字
给定一个非负整数 N,找出小于或等于 N 的最大的整数,同时这个整数需要满足其各个位数上的数字是单调递增。
(当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。)
示例 1:
输入: N = 10
输出: 9
示例 2:
输入: N = 1234
输出: 1234
示例 3:
输入: N = 332
输出: 299
说明: N 是在 [0, 10^9] 范围内的一个整数。
class Solution:
def monotoneIncreasingDigits(self, N: int) -> int:
# 将整数转换为字符串
strNum = str(N)
# flag用来标记赋值9从哪里开始
# 设置为字符串长度,为了防止第二个for循环在flag没有被赋值的情况下执行
flag = len(strNum)
# 从右往左遍历字符串
for i in range(len(strNum) - 1, 0, -1):
# 如果当前字符比前一个字符小,说明需要修改前一个字符
if strNum[i - 1] > strNum[i]:
flag = i # 更新flag的值,记录需要修改的位置
# 将前一个字符减1,以保证递增性质
strNum = strNum[:i - 1] + str(int(strNum[i - 1]) - 1) + strNum[i:]
# 将flag位置及之后的字符都修改为9,以保证最大的递增数字
for i in range(flag, len(strNum)):
strNum = strNum[:i] + '9' + strNum[i + 1:]
# 将最终的字符串转换回整数并返回
return int(strNum)
968.监控二叉树
力扣题目链接(opens new window)
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:

输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
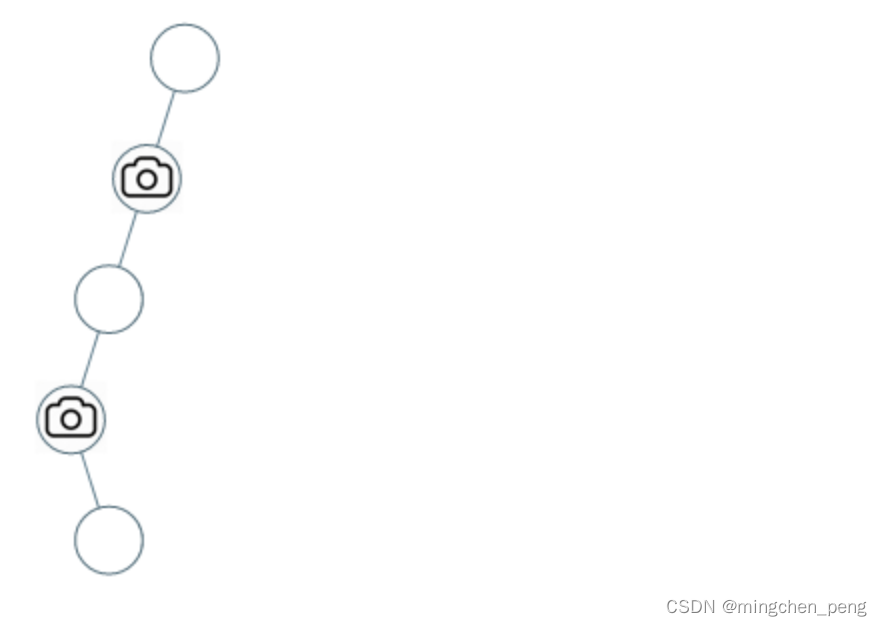
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。
class Solution:
# Greedy Algo:
# 从下往上安装摄像头:跳过leaves这样安装数量最少,局部最优 -> 全局最优
# 先给leaves的父节点安装,然后每隔两层节点安装一个摄像头,直到Head
# 0: 该节点未覆盖
# 1: 该节点有摄像头
# 2: 该节点有覆盖
def minCameraCover(self, root: TreeNode) -> int:
# 定义递归函数
result = [0] # 用于记录摄像头的安装数量
if self.traversal(root, result) == 0:
result[0] += 1
return result[0]
def traversal(self, cur: TreeNode, result: List[int]) -> int:
if not cur:
return 2
left = self.traversal(cur.left, result)
right = self.traversal(cur.right, result)
# 情况1: 左右节点都有覆盖
if left == 2 and right == 2:
return 0
# 情况2:
# left == 0 && right == 0 左右节点无覆盖
# left == 1 && right == 0 左节点有摄像头,右节点无覆盖
# left == 0 && right == 1 左节点无覆盖,右节点有摄像头
# left == 0 && right == 2 左节点无覆盖,右节点覆盖
# left == 2 && right == 0 左节点覆盖,右节点无覆盖
if left == 0 or right == 0:
result[0] += 1
return 1
# 情况3:
# left == 1 && right == 2 左节点有摄像头,右节点有覆盖
# left == 2 && right == 1 左节点有覆盖,右节点有摄像头
# left == 1 && right == 1 左右节点都有摄像头
if left == 1 or right == 1:
return 2