基本原理
逻辑回归（Logistic Regression，LR）也称为"对数几率回归"，又称为"逻辑斯谛"回归。

logistic回归又称logistic 回归分析 ，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。 逻辑回归根据给定的自变量数据集来估计事件的发生概率，由于结果是一个概率，因此因变量的范围在 0 和 1 之间。

知识点提炼
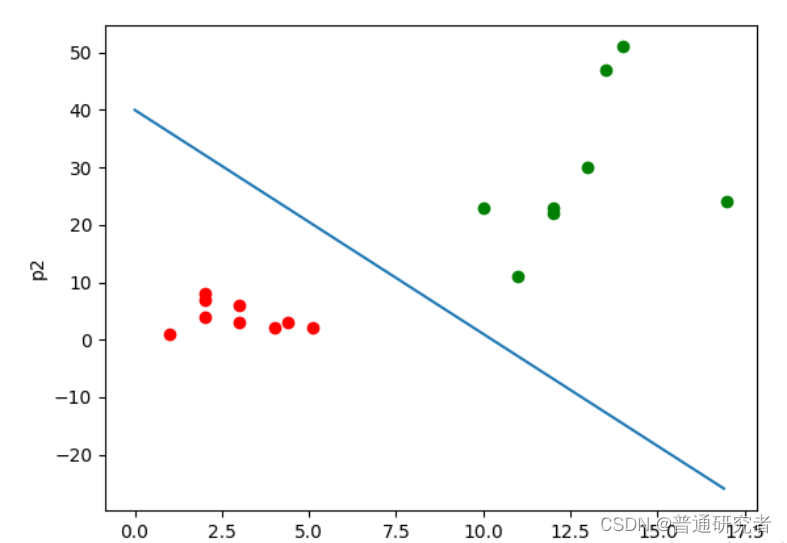
分类，经典的二分类算法！
逻辑回归就是这样的一个过程：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。
Logistic 回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别）
回归模型中，y 是一个定性变量，比如 y = 0 或 1，logistic 方法主要应用于研究某些事件发生的概率。
逻辑回归的本质：极大似然估计
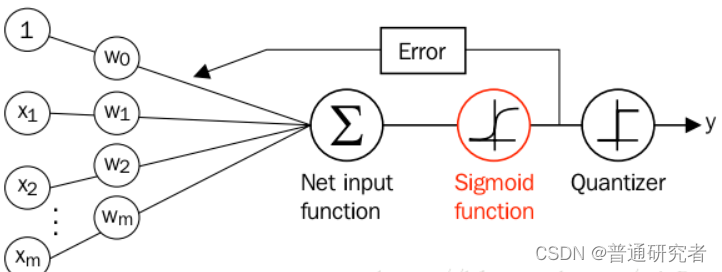
逻辑回归的激活函数：Sigmoid
逻辑回归的代价函数：交叉熵
逻辑回归的优缺点
优点：
1）速度快，适合二分类问题
2）简单易于理解，直接看到各个特征的权重
3）能容易地更新模型吸收新的数据
缺点：
对数据和场景的适应能力有局限性，不如决策树算法适应性那么强

逻辑回归中最核心的概念是 Sigmoid 函数，Sigmoid函数可以看成逻辑回归的激活函数。

下图是逻辑回归网络：

对数几率函数（Sigmoid）：
$y=\sigma (z)=\frac{1}{1+e^{-z}}$

通过对数几率函数的作用，我们可以将输出的值限制在区间[0，1]上，p(x) 则可以用来表示概率 p(y=1|x)，即当一个x发生时，y被分到1那一组的概率。可是，等等，我们上面说 y 只有两种取值，但是这里却出现了一个区间[0, 1]，这是什么鬼？？其实在真实情况下，我们最终得到的y的值是在 [0, 1] 这个区间上的一个数，然后我们可以选择一个阈值，通常是 0.5，当 y > 0.5 时，就将这个 x 归到 1 这一类，如果 y< 0.5 就将 x 归到 0 这一类。但是阈值是可以调整的，比如说一个比较保守的人，可能将阈值设为 0.9，也就是说有超过90%的把握，才相信这个x属于 1这一类。了解一个算法，最好的办法就是自己从头实现一次。下面是逻辑回归的具体实现。

Regression 常规步骤

1、寻找h函数（即预测函数）
2、构造J函数（损失函数）
3、想办法（迭代）使得J函数最小并求得回归参数（θ）
函数h(x)的值有特殊的含义，它表示结果取1的概率，于是可以看成类1的后验估计。因此对于输入x分类结果为类别1和类别0的概率分别为：
P(y=1│x;θ)=hθ (x)
P(y=0│x;θ)=1-hθ (x)

代价函数
逻辑回归一般使用交叉熵作为代价函数。关于代价函数的具体细节，请参考代价函数。

神经元的目标是去计算函数 y, 且 y = y(x)。但是我们让它取而代之计算函数 a, 且 a = a(x) 。假设我们把 a 当作 y 等于 1 的概率，1−a 是 y 等于 0 的概率。那么，交叉熵衡量的是我们在知道 y 的真实值时的平均「出乎意料」程度。当输出是我们期望的值，我们的「出乎意料」程度比较低；当输出不是我们期望的，我们的「出乎意料」程度就比较高。

交叉熵代价函数如下所示：

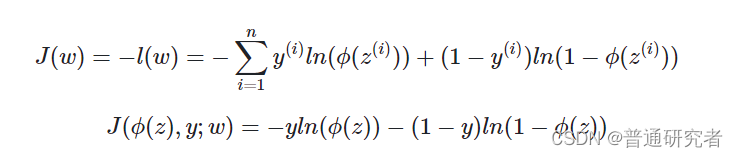
注：为什么要使用交叉熵函数作为代价函数，而不是平方误差函数？请参考：逻辑回归算法之交叉熵函数理解

逻辑回归伪代码

初始化线性函数参数为1
构造sigmoid函数
重复循环I次
	计算数据集梯度
	更新线性函数参数
确定最终的sigmoid函数
输入训练（测试）数据集
运用最终sigmoid函数求解分类

极大似然估计（Maximum Likelihood Estimation，MLE）

极大似然估计法（the Principle of Maximum Likelihood ）由高斯和费希尔（R.A.Figher）先后提出，是被使用最广泛的一种参数估计方法，该方法建立的依据是直观的最大似然原理。

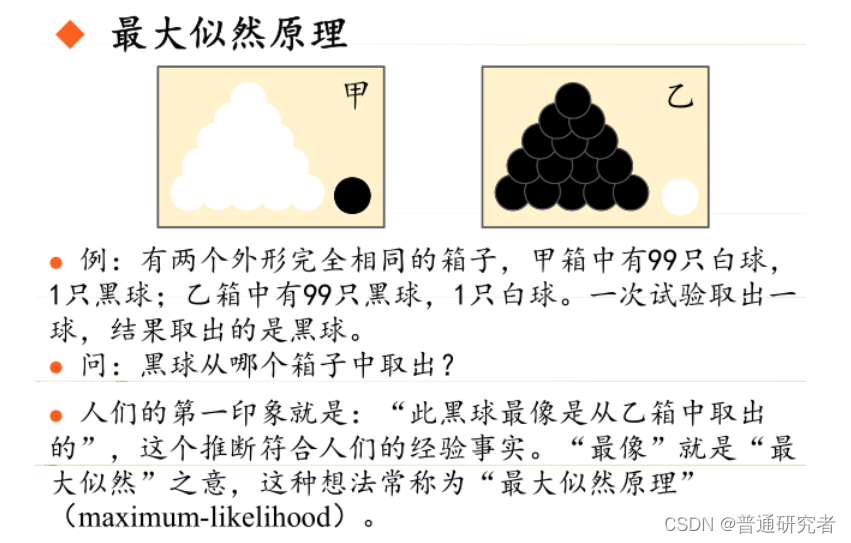
简介：

极大似然估计是一种用于估计概率分布参数的统计方法。其核心思想是通过最大化似然函数，选择使得观测数据出现的概率最大的参数值。在统计学中，似然函数度量了在给定参数下观察到某一组数据的概率。

总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

---

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

---

极大似然估计可以拆成三个词，分别是“极大”、“似然”、“估计”，分别的意思如下：
极大：最大的概率
似然：看起来是这个样子的
估计：就是这个样子的
连起来就是，最大的概率看起来是这个样子的那就是这个样子的。

---

举个例子：
有两个妈妈带着一个小孩到了你的面前，妈妈A和小孩长得很像，妈妈B和小孩一点都不像，问你谁是孩子的妈妈，你说是妈妈A。好的，那这种时候你所采取的方式就是极大似然估计：妈妈A和小孩长得像，所以妈妈A是小孩的妈妈的概率大，这样妈妈A看来就是小孩的妈妈，妈妈A就是小孩的妈妈。
总结：极大似然估计就是在只有概率的情况下，忽略低概率事件直接将高概率事件认为是真实事件的思想。

---

基本概念：

1. 似然函数： 对于参数 ( $\theta$ ) 和观测数据集 ( $X$ )，似然函数 ( L($\theta$ | $X)$ ) 表示在给定参数 ( $\theta$ ) 下观察到数据 ( $X$) 的概率。

$L(\theta |X)=P(X|\theta )$

2. 极大似然估计： 极大似然估计的目标是找到能最大化似然函数的参数值。通常采用对数似然函数（对数似然估计）进行求解，因为对数函数的增减性与原函数一致，方便求导。

   $\text{Log-Likelihood}(\theta |X)=\log L(\theta |X)$

   极大似然估计问题可以形式化为：

   ${\hat{\theta }}_{\text{MLE}}=\arg {\max }_{\theta }\log L(\theta |X)$

举例：

考虑一个简单的二项分布（二分类问题）：假设观测到了 ( $n$) 次独立的二元实验，其中有 ( $k$) 次成功。成功的概率为 ( $p$)，失败的概率为 ( $1-p$)。则似然函数为：

$L(p|k,n)=(\genfrac{}{}{0ex}{}{n}{k})p^k(1-p{)}^{n-k}$

对数似然函数为：

$\text{Log-Likelihood}(p|k,n)=k\log (p)+(n-k)\log (1-p)$

最大化对数似然函数，可以得到 ( $p$) 的极大似然估计。

面试考点：

1. 理解似然函数： 能够解释似然函数的含义，即在给定参数下观测到当前数据的可能性。

2. 极大似然估计的求解： 理解如何通过最大化似然函数或对数似然函数来估计参数，以及这一过程的数学推导。

3. 应用场景： 理解极大似然估计在不同概率分布、机器学习模型参数估计等方面的应用。

4. 性质与假设： 了解极大似然估计的一些性质，以及估计中的一些假设条件。

5. 比较： 能够与贝叶斯估计等其他参数估计方法进行比较，理解它们之间的异同。

6. 实际问题： 在实际问题中能够应用极大似然估计，例如在统计学、机器学习中的具体场景。