文章目录
- 前言
- 一、在对裁剪坐标归一化设置NDC时,DirectX平台Z的特殊
- 二、在图形计算器中,看一下Z值反转前后变化
- 1、在图形计算器创建两个变量 n 和 f 分别 控制近裁剪面 和 远裁剪面
- 2、带入公式得到齐次裁剪空间下Z值
- 3、进行透视除法
- 4、用 1 - Z 得出Z值反转前的函数图形
- 5、进行Z值反转的原因
- 在这里插入图片描述
- 三、为什么浮点值计算会存在误差
前言
在之前推导正交相机 或 透视相机 到 裁剪空间的矩阵的归一化设置坐标NDC时。我们在DirectX平台下,都进行了Z值的反转。
一、在对裁剪坐标归一化设置NDC时,DirectX平台Z的特殊
-
在OpenGL下,我们归一化设置的Z坐标在归一化后范围为[-1,1]
-
在DirectX下,我们归一化设置的Z坐标在归一化后范围为应该为[0,1]
-
但是,却使用了Reversed-Z对Z值进行了反转[1,0]
-
DirectX下进行了反转后的矩阵
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n f − n n f f − n 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n}{f-n} &\frac{nf}{f-n}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000f−nn−100f−nnf0
二、在图形计算器中,看一下Z值反转前后变化
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n f − n n f f − n 0 0 − 1 0 ] ⋅ [ x v y v z v 1 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n}{f-n} &\frac{nf}{f-n}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} · \begin{bmatrix} x_v\\ y_v\\ z_v\\ 1\\ \end{bmatrix} w2n0000h2n0000f−nn−100f−nnf0 ⋅ xvyvzv1
- Z值公式 = n f − n z v + n f f − n \frac{n}{f-n}z_v+\frac{nf}{f-n} f−nnzv+f−nnf
1、在图形计算器创建两个变量 n 和 f 分别 控制近裁剪面 和 远裁剪面
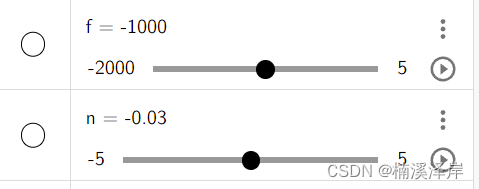
2、带入公式得到齐次裁剪空间下Z值
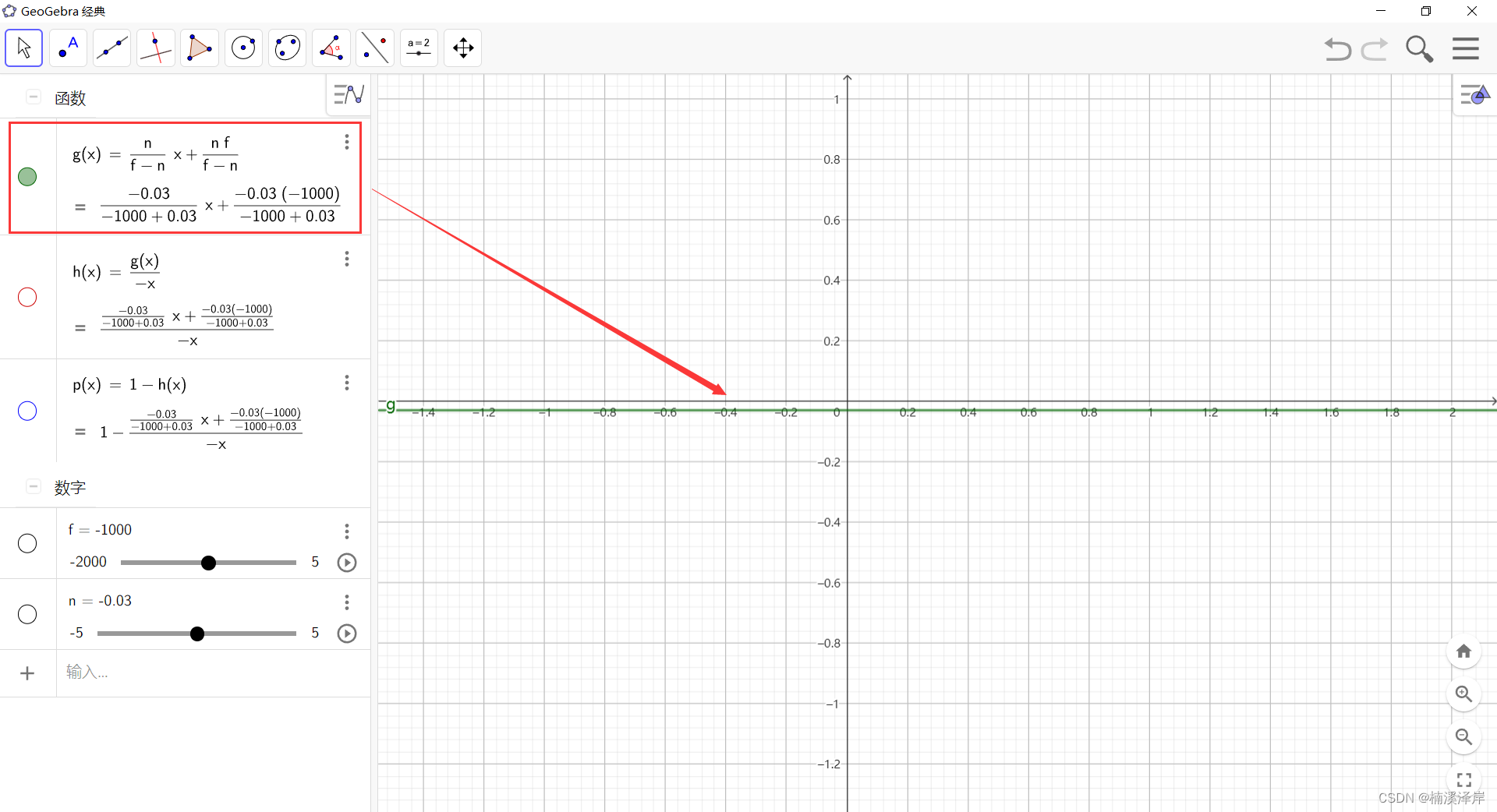
3、进行透视除法
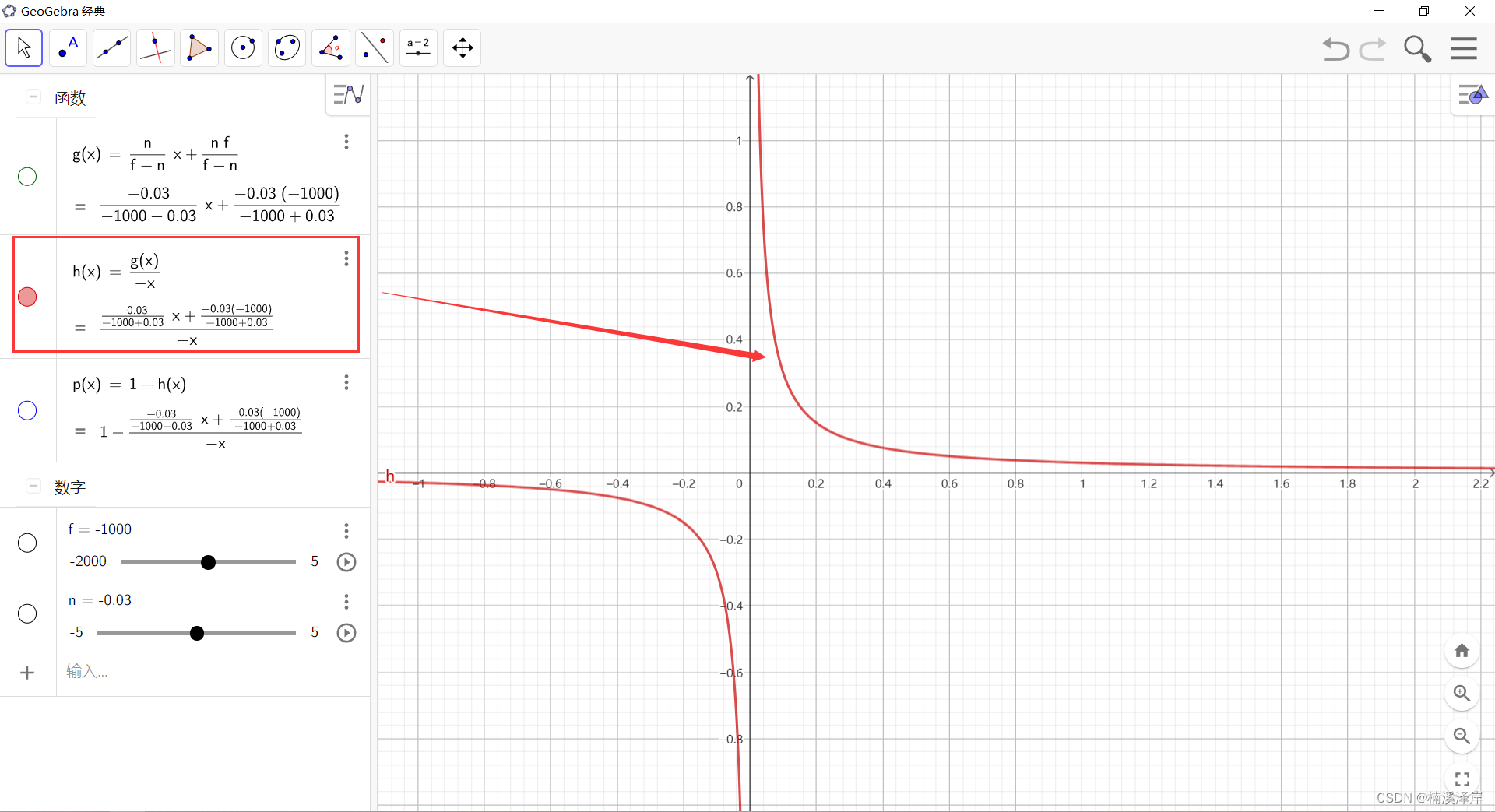
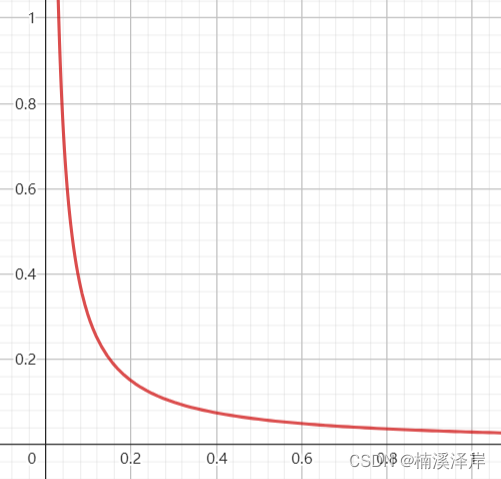
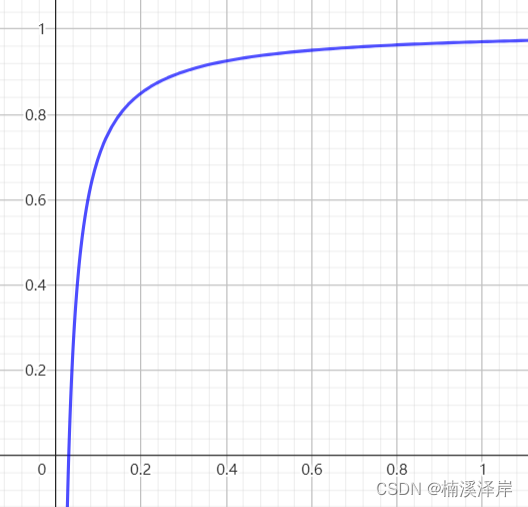
4、用 1 - Z 得出Z值反转前的函数图形
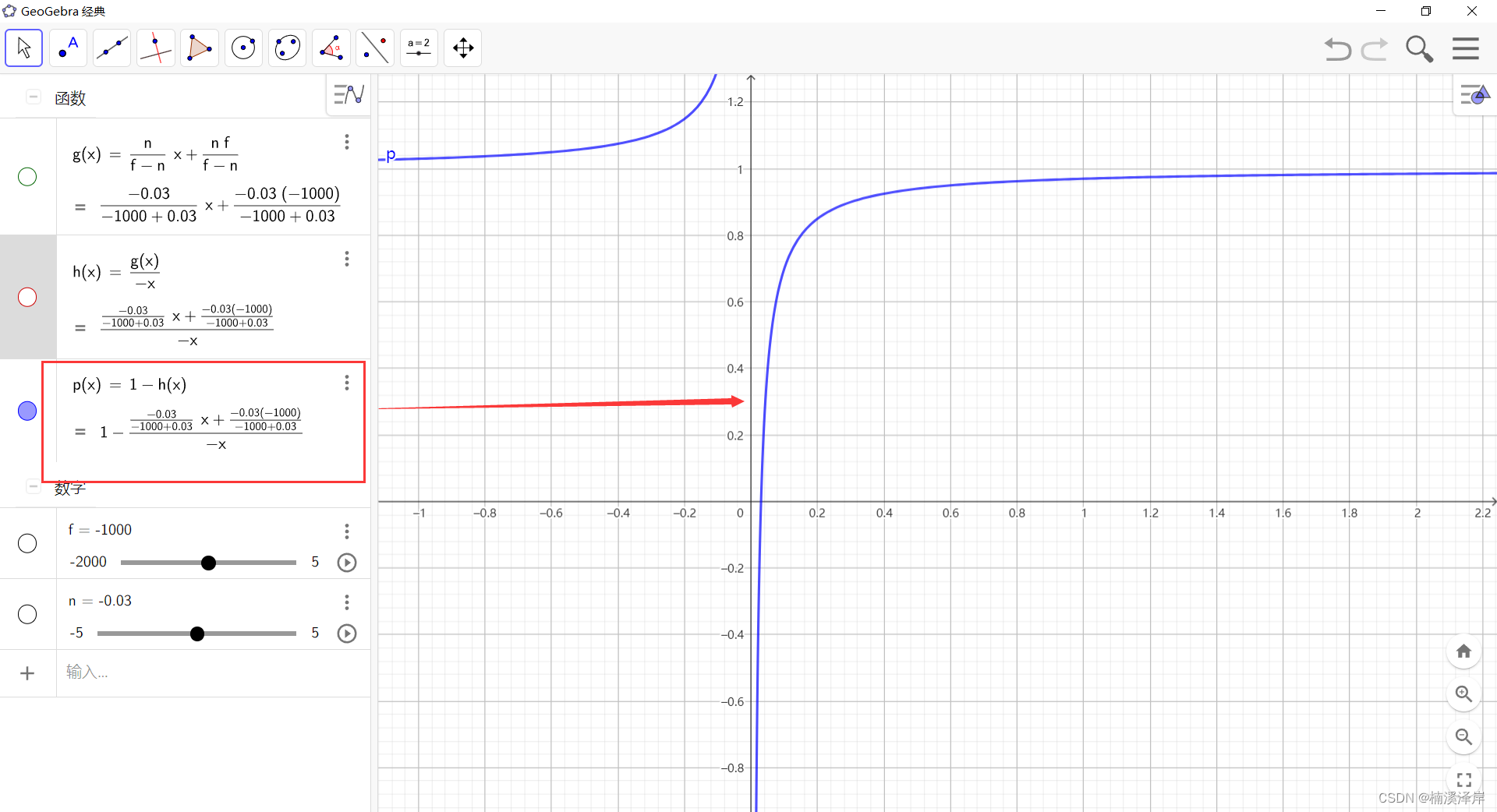
5、进行Z值反转的原因
在进行计算时,浮点值 在十进制 和 二进制 之间转化计算会造成误差
从而导致结果不是我们想要的结果。
- 在Z值反转前的函数中,可以看出我们函数在[0,0.1]之间斜率很大,导致在这 1 10 \frac{1}{10} 101 定义域中,对计算前的Zv精度要求越低。
- 但是,在其余的(0.1,1]之间斜率太小,导致在 9 10 \frac{9}{10} 109 定义域中,对计算前的 Zv精度要求越高。
这与我们实际需要的效果不符合
应该在离摄像机近时,精度高一点
离摄像机远时,精度低一点
- 所以,有了Z值的反转
三、为什么浮点值计算会存在误差
在我们的计算机中,我们的计算最后都会转化为二进制。
在我们的寄存器存储小数时,会把十进制小数转化到二进制中 ,存储不下的、靠右的部分舍弃,以保证我们的计算能够正常运行
- 小数的十进制转二进制