目录
- 选择排序
- 概念
- 算法思想
- 示例
- 步骤1
- 步骤2
- 步骤...n
- 最后一步
- 代码实现
- 时间复杂度
- 空间复杂度
- 特性总结
选择排序
概念
选择排序(Selection Sort)是一种简单直观的排序算法。基本思想是在未排序的序列中找到最小(或最大)元素,然后将其放到序列的起始位置,再从剩余未排序的序列中找到最小(或最大)元素,放到已排序序列的末尾。以此类推,直到整个序列排序完成。
算法思想
主要思路就是找出未排序的序列中的最小/最大的元素,置换到有序序列的尾巴上,实现有序序列的升序/降序效果。当有序序列的长度等于数组长度时,数组排序完成。我们拿实现升序的选择排序来进行模拟演变。
示例
如下是数组arr1 = { 6 , 4 , 3 , 9 , 2 , 1 , 5 , 7 , 8 }初始状态下的图文演示:
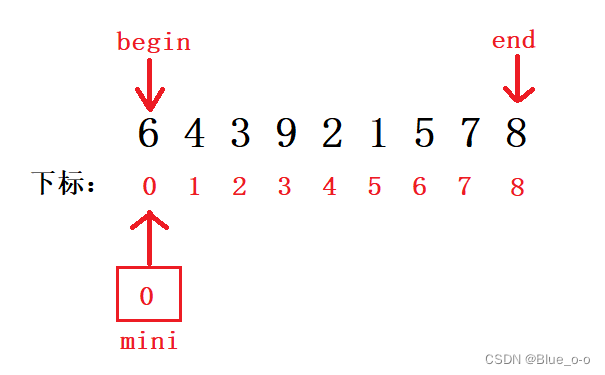
其中,变量begin、end是数组的第一个和最后一个元素的下标,变量mini用来存储未排序数组的最小元素的下标。
步骤1
第一次,在为排序的数组序列中,找到序列中最小的元素的下标:
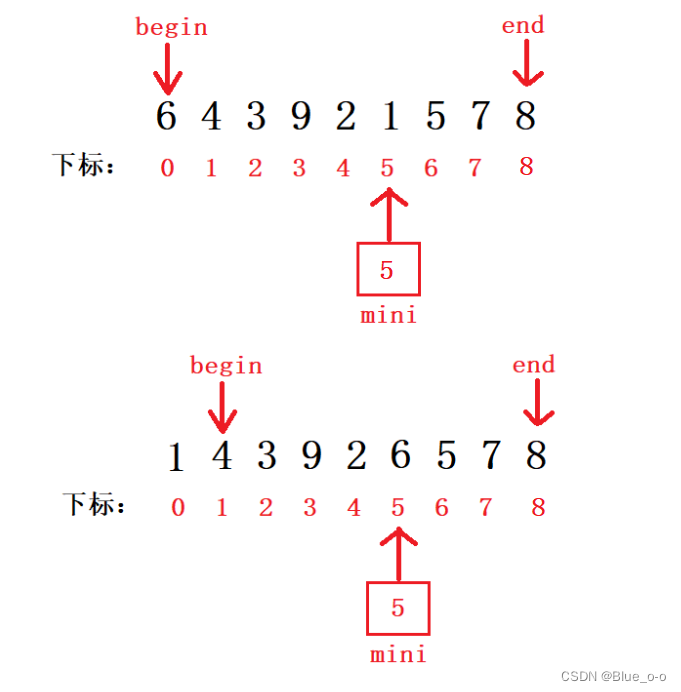
如图,找到最小的元素1,将元素1的下标5存到mini变量中,然后将arr1[begin] 和 arr1[mini] 两个元素位置互换,begin再加1,因为begin是未排序的序列的第一个元素的下标值。
步骤2
第二次,继续在为排序的数组序列中,找到序列中最小的元素的下标:
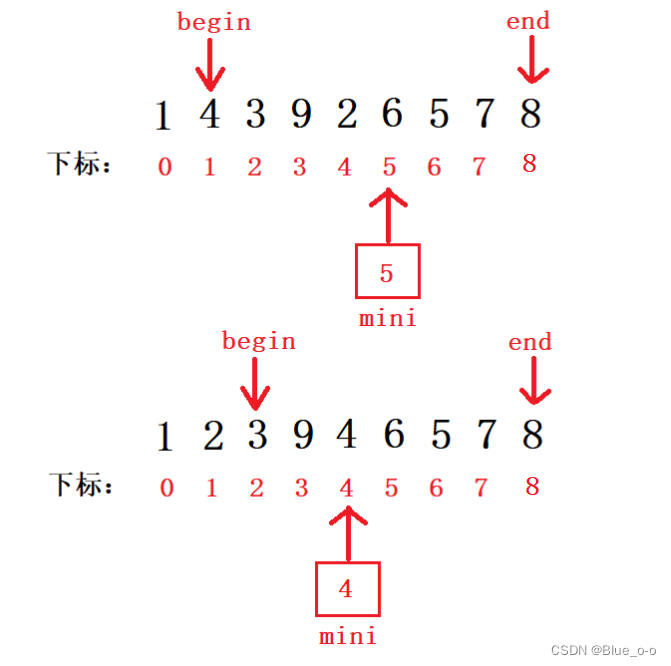
在未排序的数组中最小的元素2的下标为4,存到mini变量中,然后将arr1[begin] 和 arr1[mini] 两个元素位置互换,begin再加1。
步骤…n
重复以上的步骤,具体的我就不多加演示,下面是最后一次的排序演示图:
最后一步
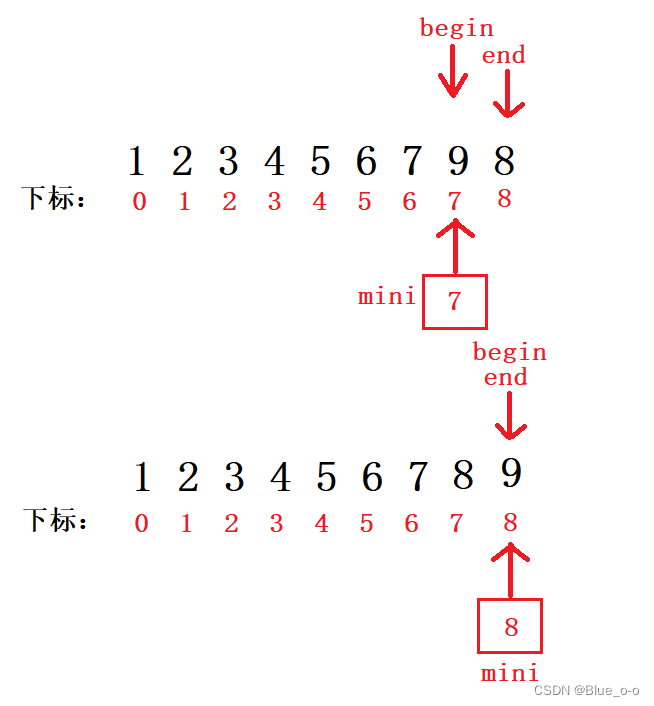
当begin和end 相等时,此时整个数组已经有序,已经排序成升序的效果。
以上便是关于选择排序的相关图形流程,下面结合图形流程,编写代码。
代码实现
选择排序的步骤如下:
初始化: 将序列分为两部分,一部分为已排序的部分,一部分为未排序的部分。初始时,已排序部分为空。
步骤2:在未排序部分中找到最小元素: 遍历未排序部分,找到最小的元素。
步骤3:交换: 将找到的最小元素与未排序部分的第一个元素交换位置,将其加入到已排序部分。
重复: 重复步骤2和步骤3,直到未排序部分为空。
代码实现:
// 交换函数
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//选择排序
void SelectSort(int* a, int n)
{
assert(a);
int begin = 0; // 有序数组的最后一个元素的下标
int end = n - 1; // 数组最后一个元素的下标
int mini = begin;
// 当begin==end时,整个数组已经排序完,退出循环。否则一直循环进行排序
while (begin < end)
{
// 在未排序的序列里找出最小的元素的下标,存到变量mini中
for (int i = begin + 1; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
}
// 将序列中最小的数组置换到前面,实现升序的排序效果
Swap(&a[begin], &a[mini]); //小的放在最前面
begin++; // 有序的数组加1,最后一个元素的下标随之加1
}
// 实现数组的升序排序。
}
以上,便是选择排序的实现代码,在此基础上,我们还可以进一步的改进。原先是在未排序的序列中找出最小/最大的元素,置换到排好序的序列的末尾中,一次只能排一个数。
现在改进点:每次排两个数,即在未排序的序列中,找出最大和最小的元素下标,分别存到变量中。然后将最大的排到最后面,最小的排到最前面(升序)。然后begin加1,end减1,接着做重复的动作,每次排好两个数。如下图:
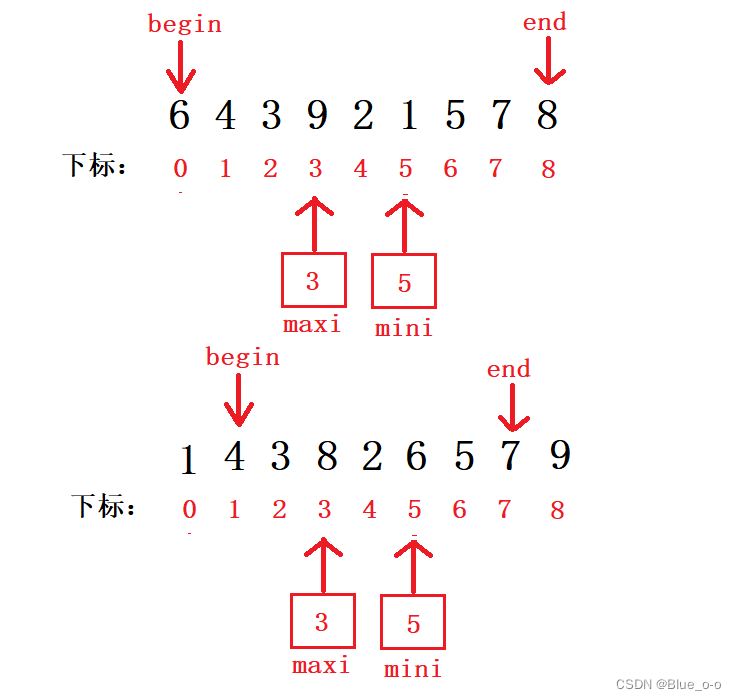
代码实现如下:
// 交换函数
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//选择排序
void SelectSort(int* a, int n)
{
assert(a);
int begin = 0;
int end = n - 1;
int maxi = begin;
int mini = begin;
while (begin < end)
{
for (int i = begin + 1; i <= end; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[end], &a[maxi]); //大的放在最后面
if (mini == end)
{
mini = maxi;
}
Swap(&a[begin], &a[mini]); //小的放在最前面
begin++;
end--;
maxi = mini = begin;
}
}
需要注意:边界的问题。
时间复杂度
O(N^2)。
不管是一次只排一个数的选择排序,还是一次排两个数的选择排序,时间复杂度都是O(N^2),当然后者肯定比前者效率更高一点,为 O(N^2 / 2),但是时间复杂度的计算是不计入系数的。所以两者的时间复杂度都是O(N^2)。
空间复杂度
O(1)。
在原数组上改动,没有用到多余的空间,所以空间复杂度为O(1)。
特性总结
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定











![解决:PermissionError: [Errno 13] Permission denied: ‘xxx’](https://img-blog.csdnimg.cn/2796e1259a1b4df695a5f9078fffebc1.gif#pic_center)