Codeforces Round 900 (Div. 3)(A-F)

news2024/11/27 19:56:54

比赛链接  :

Dashboard - Codeforces Round 900 (Div. 3) - Codeforces

A. How Much Does Daytona Cost?

题面 : 

思路 :

在序列中只要找到k，就返回true ;

代码 : 

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'

using namespace std;
typedef long long LL;
const int N = 2e5+10;

inline void solve(){
	int n , k ; cin >> n >> k ;
	bool tag = false;
	for(int i=0;i<n;i++){
		int x ; cin >> x ;
		if(x==k) tag = true;
	}
	if(tag) cout << "Yes" << endl;
	else cout << "No" << endl;
	return ;
}
 
int main()
{
    IOS
    int _ = 1;
    cin >> _;
    while(_ --) solve();
    return 0;
}

B. Aleksa and Stack

题面 : 

思路 :

在这道题中，只要满足任意两个相邻数的和，不能够不是3的倍数，且数组单调递增，那么便可以构造出这样一个序列，每两个相邻数中第一个数 mod 3 = 0,另一个数mod 3 = 1 ,然后递增的话，就可以使a1 = 3 *1 , a2= a1 + 1,a3 = 3 * 2,a4 = a3 + 1，即可满足题目条件；

代码

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'

using namespace std;
typedef long long LL;
int gcd(int a,int b){ return b==0 ? a : gcd(b,a%b); }
int lcm(int a,int b){ if(a==0||b==0) return 0; return (a*b)/gcd(a,b); }
bool is_prime(int x){if(x<2) return false;
for(int i=2;i<=x/i;i++) if(x%i==0) return false; return true;}
//numbers.erase(std::unique(numbers.begin(), numbers.end()), numbers.end()); // 去重操作
const int N = 2e5+10;

// 任意两个数的和不是3的倍数 

// 0, 1, 2
// 3 , 4 , 6, 7 

inline void solve(){
	int n ; cin >> n ;
	int x = 3;
	while(n>1){
		cout << x << " " << x + 1 << " ";
		x += 3;
		n -= 2;
	}
	if(n) cout << x ;
	cout << endl ;
	return ;
	
}
 
int main()
{
    IOS
    int _ = 1;
    cin >> _;
    while(_ --) solve();
    return 0;
}

 C. Vasilije in Cacak

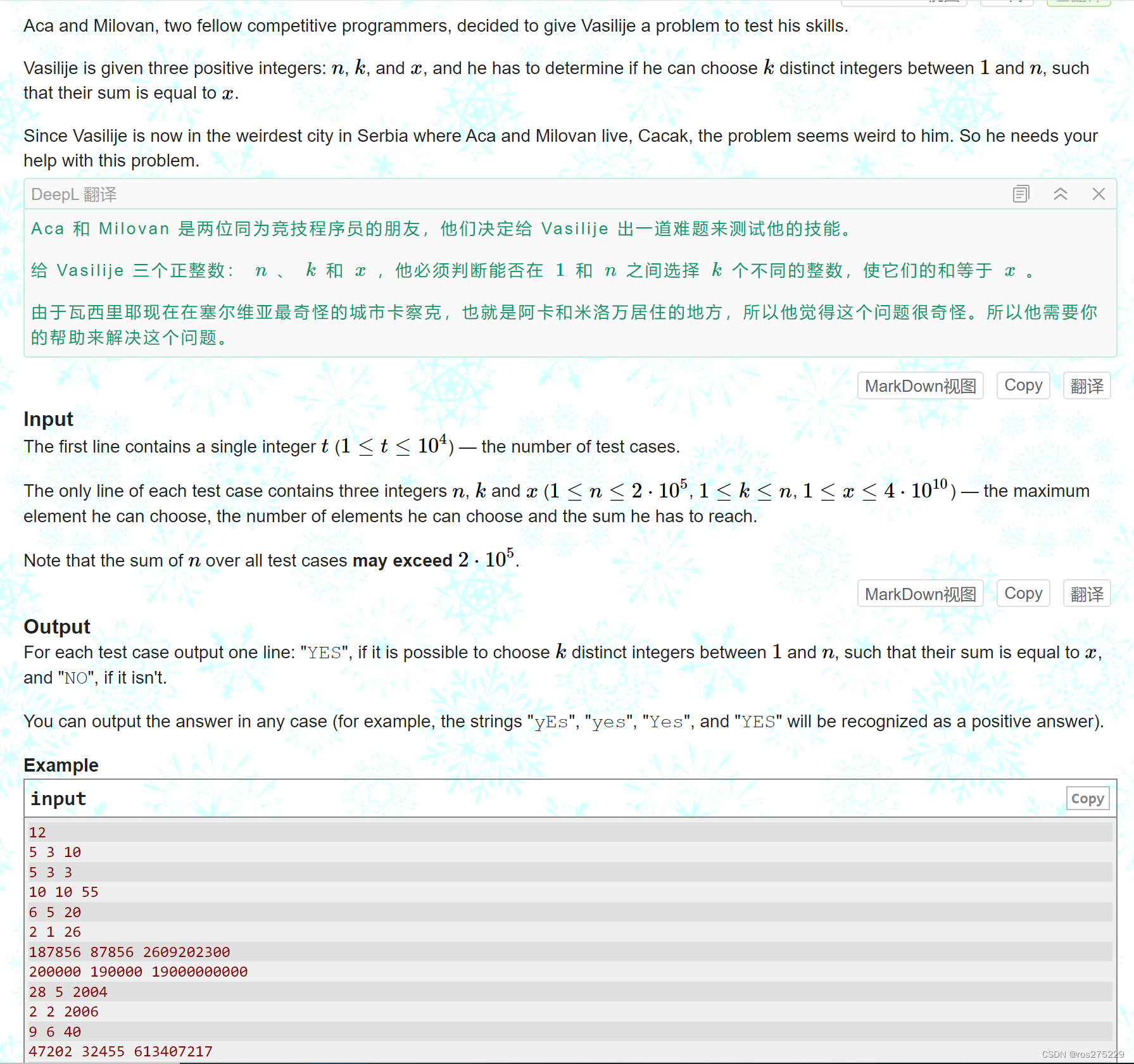
题面 : 

思路 : 

对于从  [1 ,n ]  中 选k个数 的 和为x;

假如 n = 2 (并且假设k = 2,下面一样):

         1,2 --> 1, 2, 3
n = 3 :

        1, 2 ,3 : 1,2,3,4,5,6 选两个 : 3-5 
n = 4 :

        1,2,3,4 : 3-7 :  

那么我们就可以发现一个规律 : 在[1,n]中取k个数和的范围是[最小的k个数相加，最大的k个数相加];

为了计算的方便，我们可以使用等差数列求和 : s = n*a1+(n-1)*n*d/2  ;

代码 : 

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'

using namespace std;
typedef long long LL;

LL n , k , x ;

// [1,n] 中 选k个数 的 和为x;

// 1,2 --> 1, 2, 3
//1, 2 ,3 : 1,2,3,4,5,6 选两个 : 3-5 
// 1,2,3,4 : 3-7 :  

// 等差数列求和 : s = n*a1+(n-1)*n*d/2 

inline void solve(){
	cin >> n >> k >> x;
	LL l = (1+k)*k/2 , r = (n+n-k+1)*k/2;
	if(x>=l && x<=r) cout << "Yes" << endl;
	else cout << "No" << endl;
	return ;
}
 
int main()
{
    IOS
    int _ = 1;
    cin >> _;
    while(_ --) solve();
    return 0;
}

D. Reverse Madness

题面

思路 : 

l和r都是单调递增的，且对于每一段区间都是不相交的，所有可以很快找到x对应的li和ri来满足li<=x && x<=ri ；

找到之后就是进行区间的反转，对于每个区间假设li = 2,ri =6,如果x = 4,则a=b=4,如果x=3,则a=3,b=5;那么说明是关于终点对称的，那么就可以使用前缀和算法，来对每个点进行反转次数的统计，如果统计次数为偶那就不用反转了，为奇，则要反转，具体请看代码；

代码

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'

using namespace std;
typedef long long LL;
const int N = 2e5+10;

inline void solve(){
	int n,k;cin >> n >> k ;
	string s ; cin >> s ;
	s = ' ' + s ;
	vector<int> l(k+1) , r (k+1) ;
	for(int i=1;i<=k;i++) cin >> l[i] ;
	for(int i=1;i<=k;i++) cin >> r[i] ;
	int q ; cin >> q ;
	vector<int> x(q+1) ;
	for(int i=1;i<=q;i++) cin >> x[i] ;
	vector<pair<int,int>> sum(n+3) ;
	for(int i=1;i<=q;i++){
		int pos = lower_bound(r.begin()+1,r.end(),x[i]) - r.begin();
		int a = min(x[i] , r[pos]+l[pos]-x[i]);
		int b = max(x[i],r[pos]+l[pos]-x[i]);
		sum[a].first++ ; sum[b+1].first--;
		sum[a].second = b ; sum[b].second = a ;
	}
	for(int i=1;i<n;i++){
		sum[i].first += sum[i-1].first ;
	}
	int start = -1 , end = -1 ;
	for(int i=1;i<=n;i++){
		if(sum[i].first % 2 == 1){
			start = i ;
			int end = sum[i].second ;
			while(start <= end){
				while(start<=end && sum[start].first % 2 == 1){
					swap(s[start],s[end]);
					start ++;
					end--;
				}
				while(start <= end && sum[start].first % 2 == 0){
					start ++;
					end -- ;
				}
			}
			i = sum[i].second ;
		}
	}
	for(int i=1;i<=n;i++) cout << s[i] ;
	cout << endl; 
}
 
int main()
{
    IOS
    int _ = 1;
    cin >> _;
    while(_ --) solve();
    return 0;
}

E. Iva & Pav

题面 :

思路 : 

// f(l,r)=al & al+1 &…& ar
// 给定一个 l , k ,求最大的r,满足f(l , r) >= k ;
// 定l,则f随着r单调递减 
// & : 按位与 

按位与的特点是，对于某一位，[l,r]上的所有数的该位上为1，结果才为1,那么我们可以采用前缀和的思想，用bit[i][j]来存[1,i]上第j位上为1的个数，具体实现请看代码，再获得bit数组之后，因为在l确定之后，f(l,r)随着r的增大具有单调递减的性质，所有可以使用二分来进行操作；

具体实现请看代码 ；

代码 : 

// f(l,r)=al & al+1 &…& ar
// 给定一个 l , k ,求最大的r,满足f(l , r) >= k ;
// 定l,则f随着r单调递减 
// & : 按位与 
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'

using namespace std;
typedef long long LL;
const int N = 2e5 + 10 ;

inline void solve(){
	int n ; cin >> n ;
	vector<array<int,32>> bit(n+1);
	for(int i=1;i<=n;i++){
		int x ; cin >> x ;
		for(int j = 0;j<32;j++){
			bit[i][j] = 0 ;
			bit[i][j] += x % 2 ;
			x /= 2 ;
			bit[i][j] += bit[i-1][j] ; // 进行前缀和操作，统计i前面j位上为1的个数 
		}	
	} 
	auto check = [&](int l,int r ,int c){
		vector<int> b(32) ;
		for(int i=0;i<32;i++){
			b[i] = bit[r][i] - bit[l-1][i] ;
		}
		int ans = 0 ;
		for(int i=0;i<32;i++){
			if(b[i]==r-l+1) ans += pow(2,i);
		}
		return ans >= c ; 
	};
	int q ; cin >> q ;
	while(q--){
		int l , k ; cin >> l >> k ;
		int L = l, R = n;
		int ans = -1 ;
		while(L<=R){
			int mid = (L+R)>>1 ;
			if(check(l,mid,k)){
				ans = mid ;
				L = mid + 1; 
			}else{
				R = mid - 1 ;
			}
		}
		cout << ans << " " ;
	}
	cout << endl ;
}
 
int main()
{
    IOS
    int _ = 1;
    cin >> _;
    while(_ --) solve();
    return 0;
}

F. Vasilije Loves Number Theory

题面 : 

思路 : 

  •  1 : n *= x，然后问是否存在一个a使得gcd(n,a)=1并且n*a的约数个数等于n，
  • gcd(n,a)=1 --> n,a互质
  • 由于n,a互质，那么 d(n)*d(a)=d(n*a)，那么就是要d(a) = n / d(n)，所以n % d(n)一定要等于零 

然后就可以通过唯一分解定理来解;

具体实现请看代码 :

代码

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'

using namespace std;
typedef long long LL;
const int N = 2e5+10;

// 1 : n *= x，然后问是否存在一个a使得gcd(n,a)=1并且n*a的约数个数等于n，
// gcd(n,a)=1 --> n,a互质
// --> d(n)*d(a)=d(n*a)，那么就是要d(a) = n / d(n)，所以n % d(n)一定要等于零 

inline void solve(){
	int n,q;cin>>n>>q;
	int cnt = 1 ; // 记录因数的数量 
	map<int,int> doc ;
	// 质因数分解 : 
	// num = b1^c1 + b2 ^c2 + .... + bn^cn ; 
	for(int i=2;i*i<=n;i++){
		// i相当于上面的b,c相当于上面的c ; 
		if(n%i==0){
			int c =  0 ;
			while(n%i==0) n/=i,c++;
			doc[i] = c ;
			cnt *= (c+1);
		}
	}
	if(n>1) doc[n] = 1 , cnt *= 2 ; // 最后剩下的n本身也是一个质因数 
	int now = cnt;auto doc2 = doc ;
	while(q--){
		int op ; cin >> op ;
		if(op == 2){
			now = cnt  ;
			doc2 = doc ;
		}else{
			int x ; cin >> x ;
			for(int i=2;i*i<=x;i++){
				if(x%i==0){
					int c =  0 ;
					while(x%i==0) x/=i,c++;
					now /= (doc2[i]+1);
					doc2[i] += c; 
					now *= (doc2[i]+1);
				}
			}
			if(x>1){
				now /= (doc2[x]+1);
				doc2[x]+=1;
				now *= (doc2[x]+1);
			}
			int t = now  ;
			for(auto it:doc2){
				int x = it.first ;
				int y = it.second ;
				while(y>0 && t % x== 0){
					t /= x ;
					y -- ;
				}
			}
			cout << (t==1?"YES":"NO")<<endl; 
		}
	}
}
 
int main()
{
    IOS
    int _ = 1;
    cin >> _;
    while(_ --) solve();
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1349209.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[Redis实战]分布式锁

[Redis实战]分布式锁

四、分布式锁 4.1 基本原理和实现方式对比 分布式锁&#xff1a;满足分布式系统或集群模式下多进程可见并且互斥的锁。 分布式锁的核心思想就是让大家都使用同一把锁&#xff0c;只要大家使用的是同一把锁&#xff0c;那么我们就能锁住线程&#xff0c;不让线程进行&#xf…
阅读更多...
机械过滤器（石英砂过滤器）和多介质过滤器的区别 工作原理动画

机械过滤器（石英砂过滤器）和多介质过滤器的区别 工作原理动画

​ 1&#xff1a;机械过滤器多介质石英砂过滤器介绍 机械过滤器&#xff1a;预处理水质的关键设备 机械过滤器&#xff0c;也被称为压力式过滤器&#xff0c;是纯水制备过程中不可或缺的预处理设备。它在水处理系统中扮演着重要的角色&#xff0c;能够有效地去除水中的悬浮物…
阅读更多...
Ubuntu(WSL)创建用户并赋予权限

Ubuntu(WSL)创建用户并赋予权限

查看当前用户 创建新用户 1&#xff09;执行如下命令创建新用户 sudo adduser mysql57 // mysql57 为新用户名&#xff0c;可自定义 2&#xff09;若待创建用户已存在&#xff0c;则先删除已存在用户&#xff0c;然后创建新用户 // 删除用户名 userdel mysql57// 删除组…
阅读更多...
lambda表达式和包装器

lambda表达式和包装器

正文开始前给大家推荐个网站&#xff0c;前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家。点击跳转到网站。 我们在使用库里的排序算法时如果排序的是自定义类型或者库里默认的排序不能满足我们则需求&…
阅读更多...
2.2 设计FMEA步骤二：结构分析

2.2 设计FMEA步骤二：结构分析

2.2.1 目的 设计结构分析的目的是将设计识别和分解为系统、子系统、组件和零件，以便进行技术风险分析。其主要目标包括： 可视化分析范围结构化表示：方块图、边界图、数字模型、实体零件识别设计接口、交互作用和间隙促进顾客和供应商工程团队之间的协作（接口责任）为功能分…
阅读更多...
PyTorch官网demo解读——第一个神经网络（4）

PyTorch官网demo解读——第一个神经网络（4）

上一篇&#xff1a;PyTorch官网demo解读——第一个神经网络&#xff08;3&#xff09;-CSDN博客 上一篇我们聊了手写数字识别神经网络的损失函数和梯度下降算法&#xff0c;这一篇我们来聊聊激活函数。 大佬说激活函数的作用是让神经网络产生非线性&#xff0c;类似人脑神经元…
阅读更多...
Delphi6函数大全4-SysUtils.pas

Delphi6函数大全4-SysUtils.pas

Delphi6函数大全4-SysUtils.pas首部 function FormatFloat(const Format: string; Value: Extended): string; $[SysUtils.pas功能 返回浮点数类型以指定格式字符串Format转换成字符串说明 FormatFloat(,.00, 1234567890) 1,234,567,890.00参考 function …
阅读更多...
[SSD 测试 1.3] 消费级SSD全生命周期测试

[SSD 测试 1.3] 消费级SSD全生命周期测试

依公知及经验整理，原创保护，禁止转载。 专栏 《深入理解SSD》 <<<< 返回总目录 <<<< 构建消费级SSD全生命周期测试，开展性能测试、兼容性测试、功能测试、环境应力测试、可靠性测试、电器检测。 以忆联消费级存储实验室为例，消费级存储实验室面积…
阅读更多...
思维链COT原理探究

思维链COT原理探究

要进行因果分析&#xff0c;需要把思维链中的不同元素拆解开来&#xff0c;然后通过控制变量实验&#xff0c;来研究不同元素对COT效果的影响。以下两篇论文的核心差异就在于: COT的变量拆解&#xff0c;以及控制变量的实验方式。 结合两篇论文的实验结论&#xff0c;可能导致…
阅读更多...
Java技术栈 —— Redis的雪崩、穿透与击穿

Java技术栈 —— Redis的雪崩、穿透与击穿

Java技术栈 —— Redis的雪崩、穿透与击穿 〇、实验的先导条件&#xff08;NginxJmeter&#xff09;一、Redis缓存雪崩、缓存穿透、缓存击穿1.1 雪崩1.2 穿透1.3 击穿 二、Redis应用场景——高并发2.1 单机部署的高并发问题与解决&#xff08;JVM级别锁&#xff09;2.2 集群部署…
阅读更多...
RK3568平台 Android13 GKI架构开发方式

RK3568平台 Android13 GKI架构开发方式

一.GKI简介 GKI&#xff1a;Generic Kernel Image 通用内核映像。 Android13 GMS和EDLA认证的一个难点是google强制要求要支持GKI。GKI通用内核映像&#xff0c;是google为了解决内核碎片化的问题&#xff0c;而设计的通过提供统一核心内核并将SoC和板级驱动从核心内核移至可加…
阅读更多...
29 UVM Command Line Processor (CLP)

29 UVM Command Line Processor (CLP)

随着设计和验证环境的复杂性增加&#xff0c;编译时间也增加了&#xff0c;这也影响了验证时间。因此&#xff0c;需要对其进行优化&#xff0c;以便在不强制重新编译的情况下考虑新的配置或参数。我们已经看到了function or task如何基于传递参数进行行为。类似地&#xff0c;…
阅读更多...
30 UVM Adder Testbench Example

30 UVM Adder Testbench Example

1 Adder Design 加法器设计在时钟的上升沿产生两个变量的加法。复位信号用于clear out信号。注&#xff1a;加法器可以很容易地用组合逻辑开发。引入时钟和重置&#xff0c;使其具有测试台代码中时钟和重置的样子/风格。 module adder(input clk, reset, input [7:0] in1, in…
阅读更多...
BikeDNA（二） OSM数据的内在分析1

BikeDNA（二） OSM数据的内在分析1

BikeDNA&#xff08;二&#xff09; OSM数据的内在分析1 该笔记本分析给定区域的 OSM 自行车基础设施数据的质量。 质量评估是“内在的”&#xff0c;即仅基于一个输入数据集&#xff0c;而不使用外部信息。 对于将 OSM 数据与用户提供的参考数据集进行比较的外在质量评估&…
阅读更多...
Halcon闭运算closing

Halcon闭运算closing

Halcon闭运算 文章目录 Halcon闭运算 闭运算的计算步骤&#xff0c;为先膨胀&#xff0c;后腐蚀。这两步操作能将看起来很接近的元素&#xff0c;如区域内部的空洞或外部孤立的点连接成一体&#xff0c;区域的外观和面积也不会有明显的改变。通俗地说&#xff0c;就是类似于“填…
阅读更多...
金蝶云星空其他出库单，审核中/审批流中可以选择序列号设置

金蝶云星空其他出库单，审核中/审批流中可以选择序列号设置

文章目录 其他出库单&#xff0c;审核中&#xff0c;审批流中可以选择序列号设置 其他出库单&#xff0c;审核中&#xff0c;审批流中可以选择序列号设置
阅读更多...
2023 总结：我在上海做程序员的第八年

2023 总结：我在上海做程序员的第八年

文章目录 生活举办了婚礼拿到上海户口输出的数据看书还不够 赚钱工作副业 专业技术开源图片分析工具 AndroidBitmapMonitor成为谷歌开发者专家学习的终极目的 健康总结历史总结 大家好&#xff0c;我是拭心。 这篇文章里&#xff0c;我将从生活、赚钱、专业技术、健康几方面总…
阅读更多...
Oracle-深入了解cache buffer chain

Oracle-深入了解cache buffer chain

文章目录 1.Cache buffer chain介绍2.Buffer cache的工作原理3 Buffer chains4.Multi-versioning of Buffers5.Latches6.诊断CBC latch等待7.解决 CBC Latch等待 1.Cache buffer chain介绍 经常看到会话等待事件“latch&#xff1a;cache buffers chain”。 如果想知道意味着什…
阅读更多...
Ubuntu安装FSearch

Ubuntu安装FSearch

文章目录 简介安装配置Fsearch的搜索路径参考资料 简介 Fsearch是Ubuntu等Linux系统中用于文件快速搜索的软件&#xff0c;类似于Windows系统中的Everything。下面介绍如何在Ubuntu系统中安装并使用Fsearch&#xff0c;只需简单几步&#xff01;&#x1f3c3;&#x1f3c3; 安…
阅读更多...
力扣LeetCode第26题 删除有序数组中的重复项

力扣LeetCode第26题 删除有序数组中的重复项

一、题目 给你一个有序数组 nums &#xff0c;请你 原地 删除重复出现的元素&#xff0c;使每个元素 只出现一次 &#xff0c;返回删除后数组的新长度。 不要使用额外的数组空间&#xff0c;你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。 示例 1&#xff1…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023