上一篇：PyTorch官网demo解读——第一个神经网络（3）-CSDN博客

上一篇我们聊了手写数字识别神经网络的损失函数和梯度下降算法，这一篇我们来聊聊激活函数。

大佬说激活函数的作用是让神经网络产生非线性，类似人脑神经元一样，人脑神经元对输入的处理是非线性的。这个说法有些抽象，其实回到我们具体的模型中，激活函数的作用是将输出约束在某个预期的范围内，同时让输入到输出符合我们预期的分布。例如sigmod函数将输出约束在0~1之间，同时如果输入在0周围，输出的差异比较大，如果输入偏离0较多，则输出的差异就比较小。

代码解读

# 激活函数
def log_softmax(x):
    return x - x.exp().sum(-1).log().unsqueeze(-1)

完整代码请参见第一篇

demo代码中使用了一个自定义的log_softmax激活函数，其实这并不是一个标准的log_softmax函数，标准的log_softmax函数如下（来自PyTorch官网）：

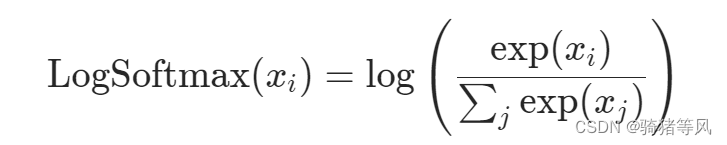
对以上公式进行一波推导得出（参见推导原文）：

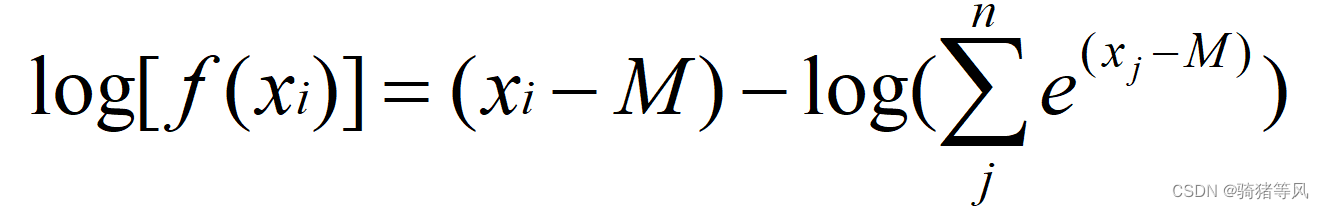
对比上面的代码发现代码里面的实现是没有减去M的，但这样也是可行的。

替换激活函数

单单看上面代码的激活函数有时候不是很好理解为什么这样做，不要激活函数可以吗？用其它激活函数又如何呢？下面我们就动手来捣鼓一下，看看换几个其它的激活函数会怎样？

首先我们把原来用log_softmax作为激活函数的结果跑出来，方便后面做对比：

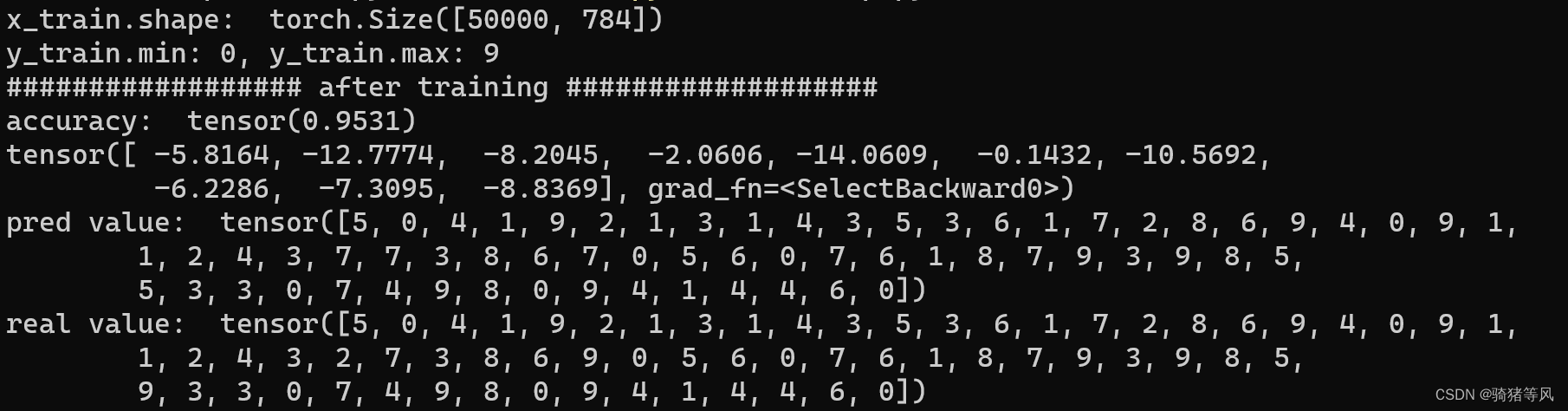
接下来我们就来替换几个激活函数看看效果。

1. 替换成softmax函数

代码：

def softmax(x):
    return x.exp() / x.exp().sum(-1).unsqueeze(-1)

运行结果：

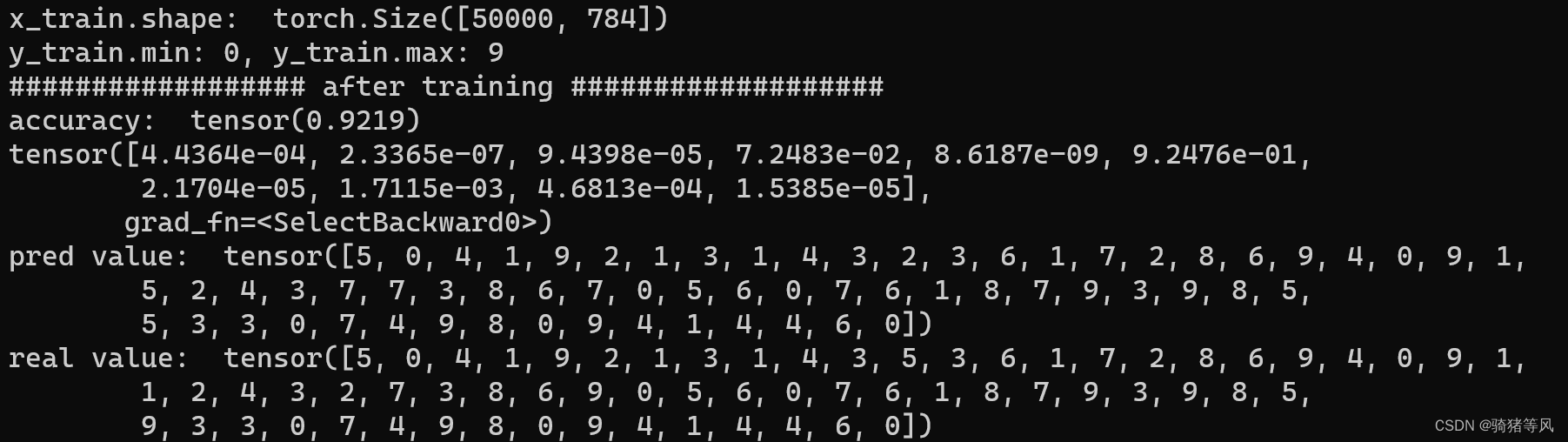
分析：

使用softmax函数训练出来的模型精度略逊于log_softmax，但不会相差太多。为什么呢？可以留言发表看法。

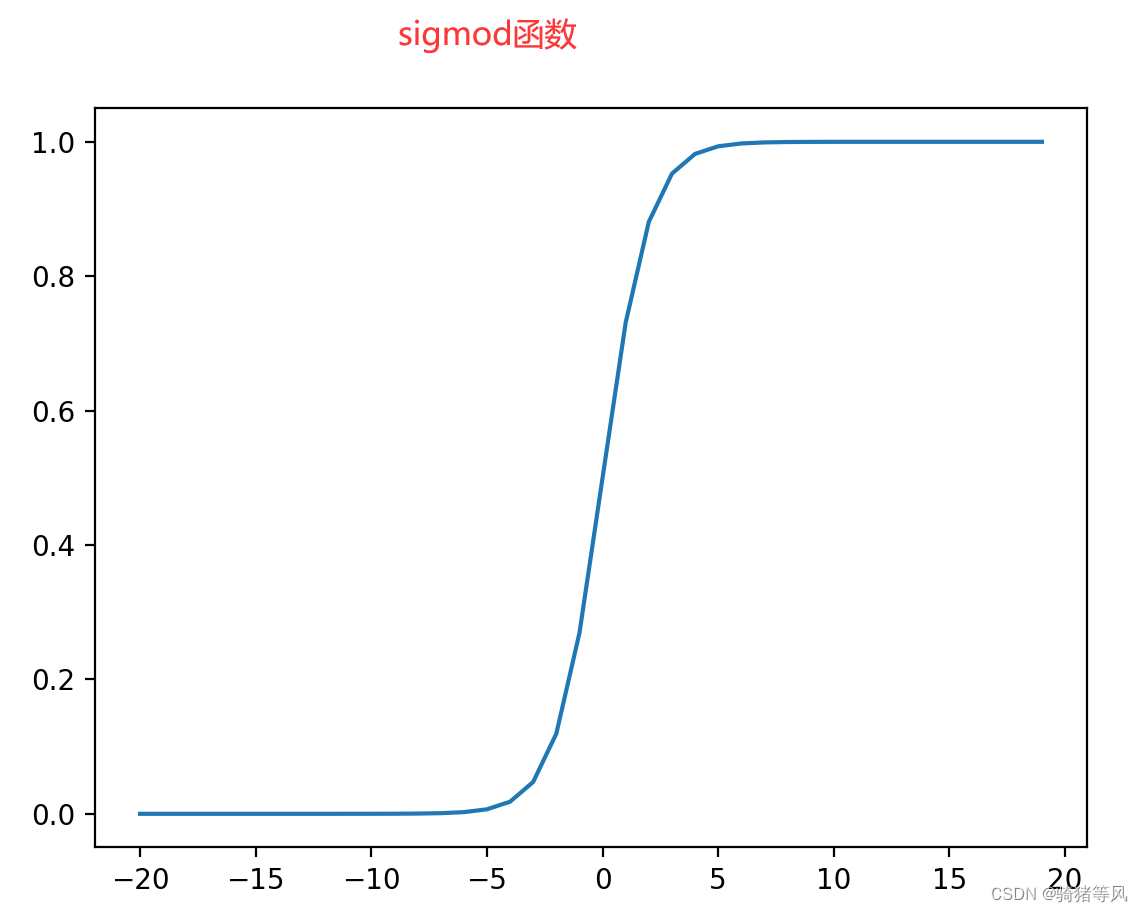
2. 替换成sigmod函数

代码：

def sigmod(x):
    return 1 / (1 + (-x).exp())

运行结果：

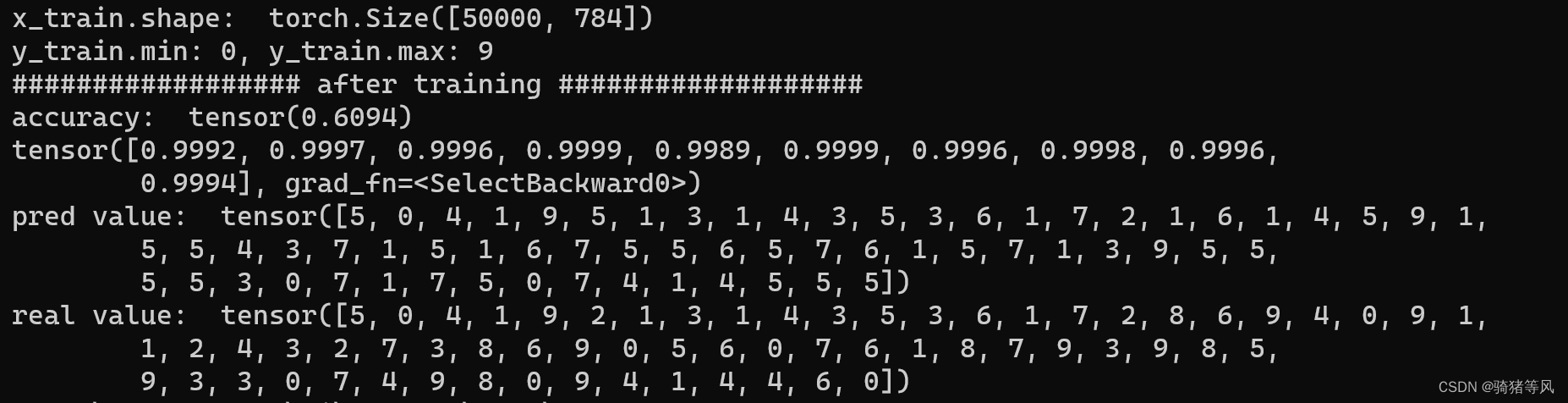
分析：

使用sigmod函数作为激活函数训练出来的模型精度只有0.6094，比使用log_softmax差很多，说明sigmod函数不能作为分类问题模型的激活函数

3. 替换成tanh函数

代码：

def tanh(x):
    p_exp = x.exp()
    n_exp = (-x).exp()
    return (p_exp - n_exp) / (p_exp + n_exp)

运行结果：

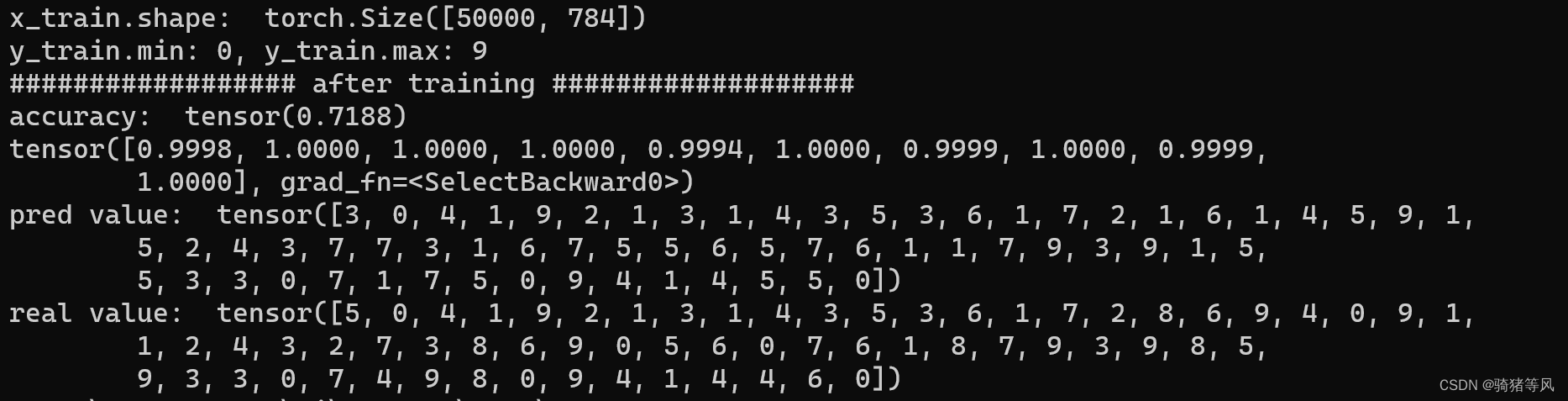
分析：

使用tanh函数作为模型的激活函数，训练出来精度为0.7188，比使用sigmod函数稍微好点，但比log_softmax还是差太多，所以tanh函数同样不适合作为分类问题模型的激活函数

总结

通过替换不同类型的激活函数，我们可以从侧面看出激活函数对于模型的重要性，也引起我们对激活函数的思考，算是抛砖引玉吧。在其它模型中如何选择激活函数呢？让我们共同学习！

如切如磋，如琢如磨！