文章总结:本文提出了使用一种生成式的模型作为MCMC算法中的建议方式,并通过GAN进行优化。
原文:Deep Involutive Generative Models for Neural MCMC
我们引入了深度内卷生成模型(一种深度生成建模的新架构),并使用它们来定义内卷神经 MCMC(一种快速神经 MCMC 的新方法)。 内卷生成模型将概率核 G ( ϕ → ϕ ′ ) G( \phi→ \phi') G(ϕ→ϕ′) 表示为包含辅助变量 π π π 的放大状态空间上的内合(即自反转)确定性函数 f ( ϕ , π ) f(\phi, π) f(ϕ,π)。 我们展示了如何使这些模型保持体积,以及如何使用深度保持体积的内卷生成模型,基于具有易于计算的接受率的辅助变量方案进行有效的 Metropolis-Hastings 更新。 我们证明深度卷合生成模型及其体积保持特例是概率核的通用逼近器。 这一结果意味着,只要有足够的网络容量和训练时间,它们就可以用于学习任意复杂的 MCMC 更新。 我们为给定模拟数据的训练参数定义损失函数和优化算法。 我们还提供了初步实验,表明内卷神经 MCMC 可以有效地探索混合蒙特卡罗难以处理的多模态分布,并且可以比最近引入的神经 MCMC 技术 A-NICE-MC 收敛得更快。
1.Introduction
神经 MCMC 是指一类新兴的深度学习方法 [21,22,16],它试图从数据中学习好的 MCMC 建议。 随着 MCMC 迭代次数的增加,神经 MCMC 方法可以保证收敛到正确的分布,这与神经变分推理 [17,13,19] 不同,后者可能会受到有偏差的近似的影响。 最近,宋等人 [21]认为内卷神经提案是可取的,但很难实现:
“如果我们的建议是确定性的,那么 fθ(fθ(x, v)) = (x, v) 对于所有 (x, v) 应该成立,但这个条件很难实现。” [21]
贡献
本文提出了[21]提出的学习内卷提案问题的解决方案。
具体来说,它提出了以下贡献:
- 1.本文介绍了对合神经网络,这是一类通过构造保证对合的新型神经网络; 我们还展示了如何将这些网络的雅可比矩阵约束为 1,即保持体积。
- 2.本文使用内卷网络定义了内卷生成模型,这是一类新的辅助变量模型,并表明体积保持模型可以用作Metropolis-Hastings提案。
-
- 本文证明了体积保持的内卷生成模型是转换核的通用逼近器,证明了它们用于良好 MCMC 建议的黑盒学习的合理性。
-
- 本文描述了一种新的、低方差的 Markov-GAN 训练目标估计器 [21],我们用它来训练内卷生成模型。
-
- 本文表明,内卷神经 MCMC 可以提高 A-NICE-MC(一种最先进的神经 MCMC 技术)的收敛速度。
-
- 本文在一个简单问题上阐述了内卷神经 MCMC。
我们通过证明几个常见的 Metropolis–Hastings 提案是内卷提案的特殊情况(第 2 节)来激发我们的方法。 然后,我们证明,通过使用一类满足适当普遍性条件(第 4 节)的精确内卷神经网络架构(第 3 节)并使用对抗性训练(第 5 节),我们可以找到经验上收敛速度极快的内卷提案(第 6 节) 。
2. Background
回想一下,Metropolis-Hastings 算法的收敛速度很大程度上取决于提议分布与后验分布的匹配程度。 为了使用给定的提议分布,通常会构造一个满足详细平衡条件的转换,该转换(在遍历设置中)确保收敛到后验。 对于一般提案来说,满足这个条件是很困难的,这导致研究人员使用较小类别的提案来解决这个问题。
我们的方法,Involutive Neural MCMC,满足通用类提案分布的详细平衡,该提案分布是从由体积保持对合函数指定的生成模型中得出的。 我们的方法建立在先前关于可逆神经网络 [1] 的工作基础上,例如,我们在普遍性的建设性证明中使用的架构使用了级联的加性耦合层 [7] [8, 12]。 我们现在描述几个现有的提案类别,并观察到每个提案都可以被视为内卷提案。
一类提议分布的典型示例是多元高斯的偏移集合。 由于它们的对称性,它们立即满足细节平衡,即前向转移的概率 P ( ϕ → ϕ ′ ) P(\phi→ \phi ' ) P(ϕ→ϕ′) 等于后向转移的概率 P ( ϕ ′ → ϕ ) P(\phi'→ \phi ) P(ϕ′→ϕ) 。 然而,多元高斯函数通常对后验的近似较差,导致收敛缓慢。 我们观察到这些提议可以被视为内卷提议:选择辅助变量 π π π 作为多元高斯的样本,并将状态转换定义为 ( ϕ , π ) → ( ϕ + π , − π ) (\phi, π) → (\phi + π, −π) (ϕ,π)→(ϕ+π,−π)。
提议分布的另一类示例是由混合蒙特卡罗算法中的哈密顿动力学生成的分布 [9]。 这些提案可以被证明满足详细的平衡,因为它们是内卷的:混合蒙特卡罗的提案是通过模拟粒子一段时间然后忽略其动量而获得的; 如果执行此操作两次,粒子将以其初始状态结束。
最近,研究人员开始使用神经网络来参数化提议分布的类别,从而产生了神经 MCMC 算法。 A-NICE-MC 方法涉及选择由可逆神经网络参数化的对称类提案:其 Metropolis-Hastings 提案将 1/2 概率分配给网络的输出,将 1/2 分配给网络的逆输出的输出网络。 该提议是对称的,因此满足细节平衡。 然而,人们也可以将其视为内卷性的。 具体来说,设
f
f
f 为可逆神经网络,
π
∼
N
(
0
,
1
)
π ∼ N(0, 1)
π∼N(0,1)为辅助变量。 定义状态转换为
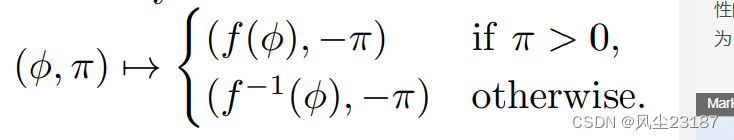
我们已经看到,所有这些例子都是内卷提案的特例。 我们现在介绍一类完全对合神经网络架构(第 3 节),并表明它们满足普遍性条件,因此可以用来任意好地近似任何对合提议(第 4 节)。
Involutive Neural Networks
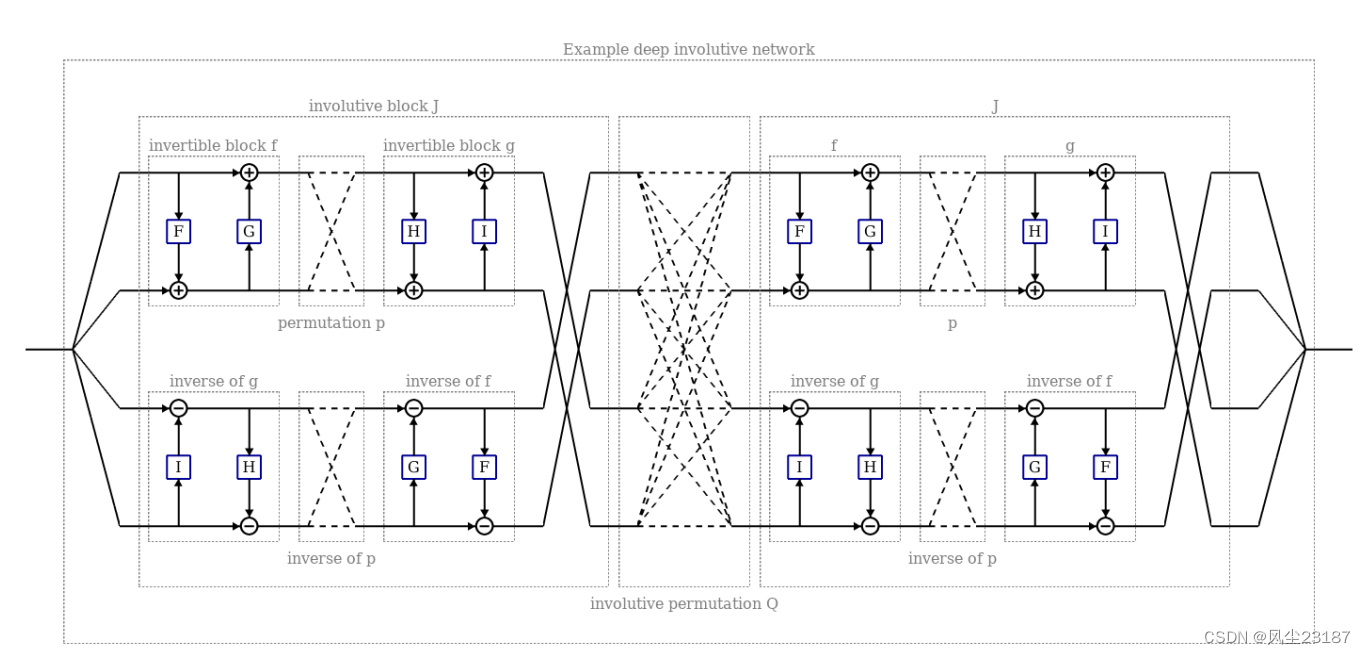
在本节中,我们将描述如何构建完全内卷的深度神经网络。 为此,我们首先描述三种较小的对合构建块,然后描述如何组合这些块以形成深度对合网络:
- 对合函数块,它们是相当一般的非线性映射,但不完全混合信息, 因为输出的每个元素都独立于输入的一半元素。
- 内卷置换块,是线性映射,无法优化,但可以混合信息。
- 包含矩阵块,它们是线性映射,但可以优化并且可以混合信息。
4.Universality of Involutive Generative Models
使用机器学习模型时,了解模型可以表示哪类函数非常有用。 在本节中,我们考虑从深度内卷网络构建的生成模型,并表明它们在某种意义上是通用逼近器。 具体来说,我们证明这些网络将状态和辅助变量 ( ϕ , π ) ∈ ( R n , R m ) (\phi, π) \in (R^n, R^m) (ϕ,π)∈(Rn,Rm) 映射到解释为另一个状态和辅助变量 ( ϕ ′ , π ′ ) (\phi' , π' ) (ϕ′,π′) 的输出,可以任意充当 R n R^n Rn 的任何紧凑子集上的高斯连续函数的良好生成模型。
5. Training and sampling algorithm
建立了对合 MCMC 过程的通用性后,我们现在描述一种训练优化的对合转移核的方法。 正如[21]中所讨论的,一个有用的转换内核满足三个标准:1)极限偏差低; 2)快速收敛; 3)低自相关性。 体积保持的对合函数导致过渡核在极限内具有零偏差(正如我们在第 4.2 节中看到的,假设遍历性),因此满足标准 1。 之前的工作表明,使用“Markov-GAN”或 MGAN 目标 [21] 可以通过在接近后验的提案和高提案接受率之间找到良好的权衡来满足标准 2。
6 Experimental Result
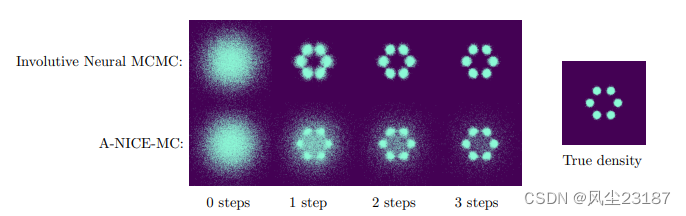
图 4:A-NICE-MC 和渐进神经 MCMC 样本的密度图。 请注意 A-NICE-MC 中剩余的异常值,这些样本从未提出过前向过渡。 几乎每个来自内卷神经 MCMC 的样本仅经过一步后就接近后验。
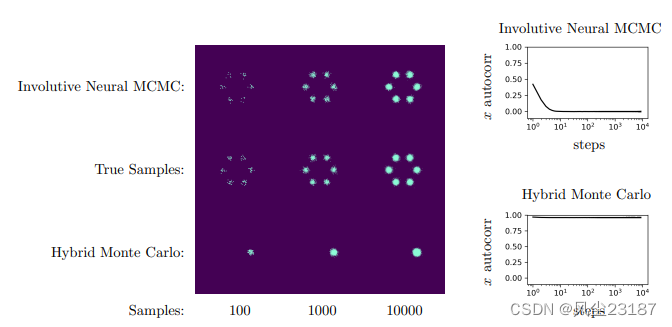
图 5:来自内卷神经 MCMC 和 HMC 的单个长链样本的密度图。 请注意,内卷神经 MCMC 在 10 步内完全混合,而 HMC 即使在 10000 步后也不会混合
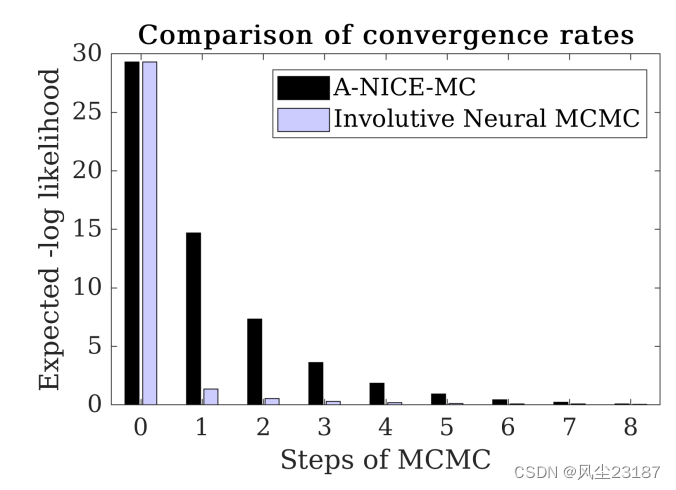
图 6:A-NICE-MC 和内卷神经 MCMC 样本相对于真实后验样本的预期负对数似然。