第四部分一维连续型随机变量

news2024/11/29 13:35:47

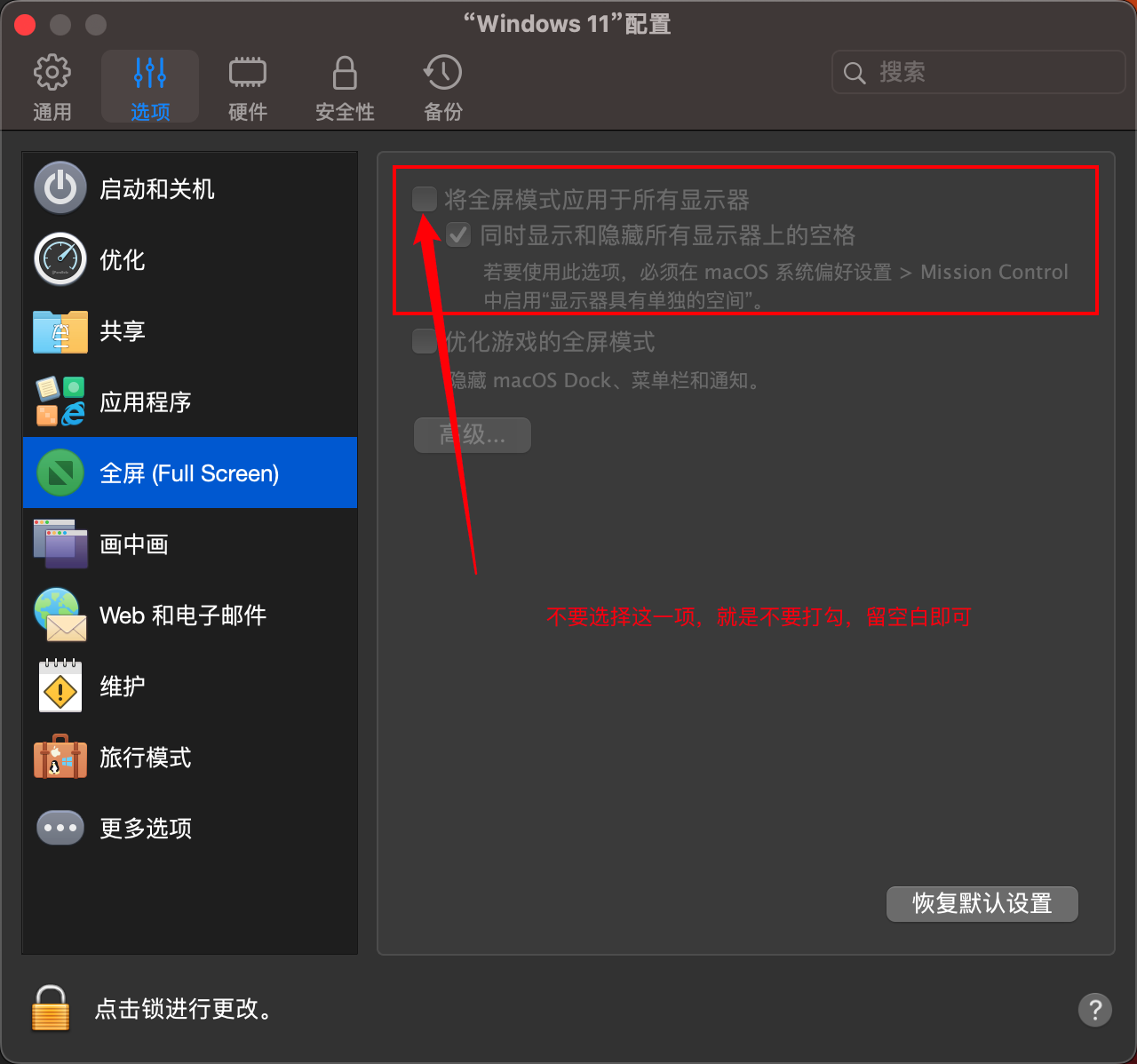
目录

温馨提示：

已知fx(X)求概率

方法：

例1

例2

求fx(X)中的未知数

方法：

例3

已知 fx(X)求F

方法：

例4

求F中的未知数

方法：

例5

已知F求f

方法：

例6

已知f求f

方法：

普通求法：

公式法：

例7

已知f求期望、方差

方法：

例8

温馨提示：

本节用到的积分结果在第三部分中计算过，不知道怎么计算的可以去看第三部分

已知fx(X)求概率

方法：

①将待求P里的式子变成X如何的式子

②P{X在ab之间}= $\int_{a}^{b}f_{x}(x)dx$

例1

设X的概率密度，已知 $Y=\frac{1}{2}X$ ，求P{0<Y<1}

解

① $P=\left \{0<\frac{1}{2}X<1 \right \}$

=P{0<X<2}

②P{0<X<2}= $\int_{0}^{2}f_{x}(x)dx$ =1 求法第三部分连续型需要的积分例1

例2

设X的概率密度，已知 $Y=\frac{1}{2}X$ ，P{Y≤y}

解

① $P=\left \{\frac{1}{2}X<y \right \}$

=P{X≤2y}

=P{-∞<X≤2y}

②P{-∞<X≤2y}= $\int_{-\infty }^{2y }f_{x}(x)dx$

求法第三部分连续型需要的积分例8

求fx(X)中的未知数

方法：

$\int_{-\infty }^{+\infty }f_{x}(x)dx$ =1

例3

设X的概率密度，试求a

解

先求出正无穷到负无穷的积分

$\int_{-\infty }^{+\infty }f_{x}(x)dx$ $=a$ 求法第三部分连续型需要的积分例4

让积分的结果等于1

a=1

已知 fx(X)求F

方法：

$F_{A}(b)\Leftrightarrow P\left \{ A\leq b\right \}$ 如果有下标则代表A≤b的括号里字母的概率

$F(b)\Leftrightarrow P\left \{ B\leq b\right \}$ 如果没有则代表括号里字母的大写字母B≤b括号里字母的概率

例4

设X的概率密度，已知 $Y=\frac{1}{2}X$ ，求 $F_{Y}(y)$

解

本题求P{Y≤y}

见本节例2 求法第三部分连续型需要的积分例8

求F中的未知数

方法：

F(+∞)=1

F(-∞)=0

F上(分段点)=F下(分段点)

解

例5

设X的分布函数为

解

$F(+\infty )=1\Rightarrow a+be^{-\lambda(+\infty ) }=1$

                         $\Rightarrow a+be^{-\infty }=1$

                         $\Rightarrow a+b\frac{1}{e^{+\infty }}=1$

                         $\Rightarrow a+b\frac{1}{+\infty }=1$

                         $\Rightarrow a+b0=1$

                         $\Rightarrow a=1$

F上(分段点)=F下(分段点) $\Rightarrow 0=1+be^{-\lambda0 }$ 两个式子在0时的取值相等

                                         $\Rightarrow 0=1+be^{0}$

                                         $\Rightarrow 0=1+b$

                                         $\Rightarrow b=-1$

已知F求f

方法：

$f_{A}(a)=F_{A}'(a)$

例6

设Y的分布函数F求 $f_Y{(y)}$

解

$\Rightarrow$

$\Rightarrow$

已知f求f

方法：

普通求法：

(麻烦但啥题都能用)

求F，F再求导就是f

公式法：

(简单，但仅满足要求的题可用)

若再 $f_{x}(x)\neq 0$ 的区间内，Y=g(X)是单调递增或者单调递减

则

①根据Y与X的关系式，算一下X=？，接着算下 $\frac{dx}{dy}$

②给 $f_{x}(x)$ 所有可能的取值后面，都 $\times |\frac{dx}{dy}|$

③将 $f_{x}(x)$ 变成 $f_{Y}(y)$

④根据Y与X的关系，用y表示所有的x

例7

设X的概率密度，已知 $Y=\frac{1}{2}X$ ，求 $f_Y{(y)}$

解

普通求法：

例6

公式法：

题目中不等于0的取值为1，Y的表达式是 $Y=\frac{1}{2}X$ ，验证Y的表达式在0≤x＜1中是不是单调递增或递减，很明显是单调递增的

①X=2Y，接着算 $\frac{dx}{dy}=\frac{d(2y)}{dy}=2$

②给 $f_{x}(x)$ 所有取值后面都 $\times |\frac{dx}{dy}|$ ，这里都×|2|

③将 $f_{x}(x)$ 变成 $f_{Y}(y)$

④

所有的x可以变为2y

最后

已知f求期望、方差

方法：

E[g(X)]= $\int_{-\infty }^{+\infty }g(x)f_{x}(x)dx$

E(aX+bY+c)=aEX+bEY+c

DX= $E(X^{2})-(EX)^{2}$

D(aX+c)= $a^{2}DX$

例8

已知，试求D(2X+3)

解

D(2X+3)=2^2DX

=4DX

=4[E(X^2)-(EX)^2]

= $4[\int_{-\infty }^{+\infty }x^{2}f_{x}(x)dx-(\int_{-\infty }^{+\infty }xf_{x}(x)dx)^{2}]$

= $4\times [\frac{1}{3}-(\frac{1}{2})^{2}]$ 求法第三部分连续型需要的积分例3，例2

= $\frac{1}{3}$