文章目录
- 前言
- 一、代数运算
- 1.手动计算流程
- 2.ubermag库函数验证
- 二、求导运算
- 1.手动计算流程
- 2.ubermag库函数验证
- 3.标量场的梯度,矢量场的散度和旋度
- 三、积分运算
- 1.手动计算流程
- 2.ubermag库函数验证
- 总结
靡不有初,鲜克有终。——《诗经·大雅·荡》
前言
前段时间遇到需要数值求解描述斯格明子运动的Thiele方程,方程中需要对有限差分场进行矢量点积,矢量叉积,求导,积分等操作,由于笔者之前对有限差分场的操作都是根据现有的ubermag库函数去实现的,对其背后的具体计算方式并不是很了解,所以去查找了一下资料学习如何手动数值计算这些方程。为了直观的理解这些数值计算差分场的流程,本文通过对ubermag官网的一个示例程序(Exercise: Domain wall pair conversion)生成的几个磁化文件进行一系列操作,从而对比验证相关库函数的计算结果。
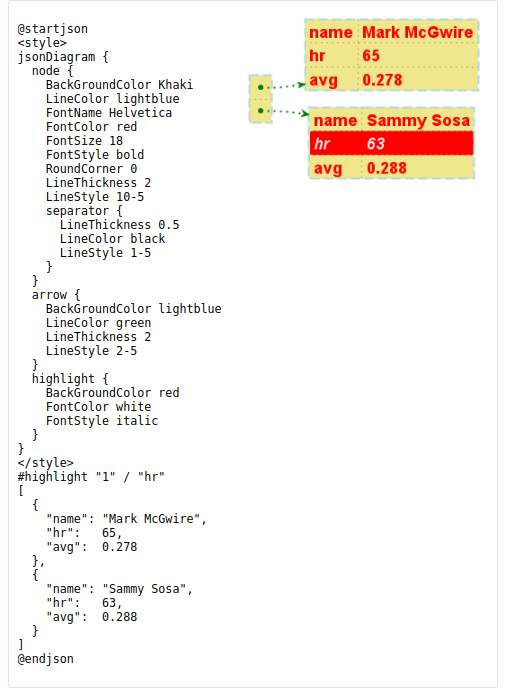
运行该示例程序并挑选弛豫后的基态文件重命名为 “mag@dw#t@0.omf”,施加电流后的第89个文件重命名为 “mag@meron#t@89.omf”,施加电流后的第199个文件重命名为 “mag@skyrmion#t@199.omf”,此外对该示例程序稍微改动一下获取弛豫后的均匀磁化文件并重命名为 “mag@uniform#t@relaxed.omf”。即挑选了分别包含畴壁对,麦纫,斯格明子,均匀磁化的矢量场文件并显示了一个单元格(125e-9,9e-9,1e-9)的矢量值(软件界面的黄色框中第二行是单元格的坐标,第一行是该单元格的矢量值),如下图所示:

#######
本文链接:https://blog.csdn.net/qq_43572058/article/details/135320445
CSDN@搬砖工人_0803号
#######
一、代数运算
1.手动计算流程
对于有限差分场的“加”,“减”,“数乘”,“数除”等代数计算,需要 逐单元格、逐元素值 进行计算,其中逐单元格要求参与计算的有限差分场的网格需要相同(即三个方向上的单元格信息相同),而逐元素值要求对有限差分场中每一个单元格所拥有的值的所有分量(标量值或者矢量值的三个分量)同步计算。比如两个矢量场相减
m
→
(
x
,
y
,
z
)
−
h
→
(
x
,
y
,
z
)
\overrightarrow{m}(x,y,z)-\overrightarrow{h}(x,y,z)
m(x,y,z)−h(x,y,z),则需要同步遍历两个矢量场的每一个单元格
(
x
0
,
y
0
,
z
0
)
(x_0,y_0,z_0)
(x0,y0,z0),并将该单元格的矢量值相减作为结果矢量场中该单元格的值
r
→
(
x
0
,
y
0
,
z
0
)
=
m
→
(
x
0
,
y
0
,
z
0
)
−
h
→
(
x
0
,
y
0
,
z
0
)
=
(
m
x
−
h
x
,
m
y
−
h
y
,
m
z
−
h
z
)
\overrightarrow{r}(x_0,y_0,z_0)=\overrightarrow{m}(x_0,y_0,z_0)-\overrightarrow{h}(x_0,y_0,z_0)=(m_x-h_x,m_y-h_y,m_z-h_z)
r(x0,y0,z0)=m(x0,y0,z0)−h(x0,y0,z0)=(mx−hx,my−hy,mz−hz)。再比如一个标量场乘以矢量场
m
x
(
x
,
y
,
z
)
⋅
h
→
(
x
,
y
,
z
)
m_x(x,y,z) \cdot \overrightarrow{h}(x,y,z)
mx(x,y,z)⋅h(x,y,z),则同时遍历两个场的每一个单元格,并将该单元格的标量值乘以矢量值作为结果矢量场中该单元格的值
r
→
(
x
0
,
y
0
,
z
0
)
=
m
x
(
x
0
,
y
0
,
z
0
)
⋅
h
→
(
x
0
,
y
0
,
z
0
)
=
(
m
x
h
x
,
m
x
h
y
,
m
x
h
z
)
\overrightarrow{r}(x_0,y_0,z_0)=m_x(x_0,y_0,z_0) \cdot \overrightarrow{h}(x_0,y_0,z_0)=(m_xh_x,m_xh_y,m_xh_z)
r(x0,y0,z0)=mx(x0,y0,z0)⋅h(x0,y0,z0)=(mxhx,mxhy,mxhz)。那么通常有以下情况:矢量场(标量场) ± 矢量场(标量场) = 矢量场(标量场);矢量场(标量场) *(/)标量场(矢量场) = 矢量场;标量场 *(/)标量场 = 标量场。此外,单个数值则可以看作空间分布均匀的标量场。
有了以上的思路,可以推断两个矢量场的点积结果是一个标量场,叉积结果是一个矢量场。对于点积的结果标量场中每一个单元格的标量值为:
r
(
x
0
,
y
0
,
z
0
)
=
m
→
(
x
0
,
y
0
,
z
0
)
⋅
h
→
(
x
0
,
y
0
,
z
0
)
=
m
x
h
x
+
m
y
h
y
+
m
z
h
z
r(x_0,y_0,z_0)=\overrightarrow{m}(x_0,y_0,z_0) \cdot \overrightarrow{h}(x_0,y_0,z_0)=m_xh_x+m_yh_y+m_zh_z
r(x0,y0,z0)=m(x0,y0,z0)⋅h(x0,y0,z0)=mxhx+myhy+mzhz。对于叉积的结果矢量场中每一个单元格的矢量值为:
r
→
(
x
0
,
y
0
,
z
0
)
=
m
→
(
x
0
,
y
0
,
z
0
)
×
h
→
(
x
0
,
y
0
,
z
0
)
=
(
m
x
x
^
+
m
y
y
^
+
m
z
z
^
)
×
(
h
x
x
^
+
h
y
y
^
+
h
z
z
^
)
\overrightarrow{r}(x_0,y_0,z_0)=\overrightarrow{m}(x_0,y_0,z_0) \times \overrightarrow{h}(x_0,y_0,z_0)=(m_x\hat{x}+m_y\hat{y}+m_z\hat{z}) \times (h_x\hat{x}+h_y\hat{y}+h_z\hat{z})
r(x0,y0,z0)=m(x0,y0,z0)×h(x0,y0,z0)=(mxx^+myy^+mzz^)×(hxx^+hyy^+hzz^),最后直接使用矢量叉积的分配律进行展开,或者使用行列式方式展开:
∣
x
^
y
^
z
^
m
x
m
y
m
z
h
x
h
y
h
z
∣
=
(
m
y
h
z
−
m
z
h
y
,
m
z
h
x
−
m
x
h
z
,
m
x
h
y
−
m
y
h
x
)
\begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ m_x & m_y & m_z \\ h_x & h_y & h_z \end{vmatrix}=(m_yh_z-m_zh_y,m_zh_x-m_xh_z,m_xh_y-m_yh_x)
x^mxhxy^myhyz^mzhz
=(myhz−mzhy,mzhx−mxhz,mxhy−myhx)。
2.ubermag库函数验证
对于上述有限差分场的代数计算可以在支持表格计算的软件中轻易实现(如:Origin、Excel),将OVF格式的有限差分场文件直接拖进表格中(矢量场有三列数据,标量场有一列数据),每一行则代表一个单元格的值。通过定义表格中的列变量,从而非常便捷的操作整列参与代数计算,计算完成后,将结果数据列重新放入一个表格中保存,并手动添加OVF格式要求的文件头尾信息并作为结果场文件。
不过利用ubermag现有的库函数对有限差分场进行代数计算则更方便,ubermag的discretisedfield类重载了算术运算符(+,-,*,/)用于实现上述的计算流程,我们使用如下代码读取前面挑选的4个矢量场文件,接着进行一些代数计算,并保存结果差分场文件:
#导入ubermag的离散场
import discretisedfield as df
#读取有限差分场文件
mag_uniform = df.Field.from_file(r'F:\software\microMag\ubermag\示例程序\CSDNBlog#FD\mag@uniform#t@relaxed.omf')
mag_dw_t0 = df.Field.from_file(r'F:\software\microMag\ubermag\示例程序\CSDNBlog#FD\mag@dw#t@0.omf')
mag_meron_t89 = df.Field.from_file(r'F:\software\microMag\ubermag\示例程序\CSDNBlog#FD\mag@meron#t@89.omf')
mag_skyrmion_t199 = df.Field.from_file(r'F:\software\microMag\ubermag\示例程序\CSDNBlog#FD\mag@skyrmion#t@199.omf')
#进行代数计算
result_algebra = 1 * mag_uniform + 0.7*(mag_dw_t0 - mag_uniform) + 0.8*(mag_meron_t89 - mag_uniform) + 0.9*(mag_skyrmion_t199 - mag_uniform)
#保存结果有限差分场
result_algebra.to_file("result_algebra.omf",representation="txt")
得到的结果差分场文件result_algebra.omf如下所示:

手动验算的结果和调用库函数的结果是完全相同的,此外,注意到通过减去背景场并按照权重系数叠加动态场的操作可以实现类似“蒙版”的视觉效果。
从上文可以推断出两个相同的归一化矢量场点积的结果为值等于1的均匀标量场,而两个相同的矢量场叉积的结果为矢量值等于 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)的均匀矢量场。我们使用以下代码来验证这个结论:
#对矢量场进行归一化
mag_skyrmion_t199_norm = mag_skyrmion_t199.orientation
#点积归一化矢量场
result_dot = mag_skyrmion_t199_norm.dot(mag_skyrmion_t199_norm)
#叉积矢量场
result_cross = mag_skyrmion_t199.cross(mag_skyrmion_t199)
#保存结果有限差分场
result_dot.to_file("result_dot.omf",representation="txt")
result_cross.to_file("result_cross.omf",representation="txt")
得到的结果差分场文件result_dot.omf和result_cross.omf如下所示:

可以看到使用库函数计算的上述结果正是我们所预想的标量场和矢量场。注意即便代码中没有报错,我们也要正确合理的使用库函数 dot() 和 cross(),它们是只能被矢量场对象调用,其参数也只能是一个矢量场对象。
二、求导运算
1.手动计算流程
给定一个三元函数
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z)的具体方程,相信随便抓一个中学生也能对其熟练求偏导,however,如何对有限差分场求偏导呢?不同于对一个具体函数直接求出偏导的解析方程,考虑到有限差分场中每个单元格的尺寸是相同的,所以可以根据泰勒展开或者直接根据偏导的定义对有限差分场近似求解数值偏导:比如矢量场
m
→
(
x
,
y
,
z
)
\overrightarrow{m}(x,y,z)
m(x,y,z) 对
x
x
x 求偏导,有
∂
m
→
(
x
,
y
,
z
)
∂
x
→
Δ
m
→
(
x
,
y
,
z
)
Δ
x
=
m
→
(
x
+
Δ
x
,
y
,
z
)
−
m
→
(
x
,
y
,
z
)
Δ
x
\frac{\partial{\overrightarrow{m}(x,y,z)}}{\partial{x}} \rarr \frac{\Delta{\overrightarrow{m}(x,y,z)}}{\Delta{x}}=\frac{\overrightarrow{m}(x+\Delta{x},y,z) - \overrightarrow{m}(x,y,z)}{\Delta{x}}
∂x∂m(x,y,z)→ΔxΔm(x,y,z)=Δxm(x+Δx,y,z)−m(x,y,z),即对于矢量场中每一个单元格来说,需要用x方向的下一个单元格的矢量值减去该单元格的矢量值,并将结果矢量值除以单元格在x方向的尺寸,最终得到一个结果矢量场。当然,也有用当前单元格的矢量值减去x方向的上一个单元格的矢量值,最后将结果矢量值除以单元格在x方向的尺寸,即
∂
m
→
(
x
,
y
,
z
)
∂
x
→
Δ
m
→
(
x
,
y
,
z
)
Δ
x
=
m
→
(
x
,
y
,
z
)
−
m
→
(
x
−
Δ
x
,
y
,
z
)
Δ
x
\frac{\partial{\overrightarrow{m}(x,y,z)}}{\partial{x}} \rarr \frac{\Delta{\overrightarrow{m}(x,y,z)}}{\Delta{x}}=\frac{\overrightarrow{m}(x,y,z) - \overrightarrow{m}(x-\Delta{x},y,z)}{\Delta{x}}
∂x∂m(x,y,z)→ΔxΔm(x,y,z)=Δxm(x,y,z)−m(x−Δx,y,z)。
以上两个方法分别是前向差分求导和后向差分求导,但是结果的误差都比较大且呈现负相关,所以可以将两种方法相加得到误差较小的中心差分求导法:
∂
m
→
(
x
,
y
,
z
)
∂
x
=
(
m
→
(
x
+
Δ
x
,
y
,
z
)
−
m
→
(
x
,
y
,
z
)
Δ
x
+
m
→
(
x
,
y
,
z
)
−
m
→
(
x
−
Δ
x
,
y
,
z
)
Δ
x
)
/
2
=
m
→
(
x
+
Δ
x
,
y
,
z
)
−
m
→
(
x
−
Δ
x
,
y
,
z
)
2
Δ
x
\frac{\partial{\overrightarrow{m}(x,y,z)}}{\partial{x}}=(\frac{\overrightarrow{m}(x+\Delta{x},y,z) - \overrightarrow{m}(x,y,z)}{\Delta{x}}+\frac{\overrightarrow{m}(x,y,z) - \overrightarrow{m}(x-\Delta{x},y,z)}{\Delta{x}})/2=\frac{\overrightarrow{m}(x+\Delta{x},y,z) - \overrightarrow{m}(x-\Delta{x},y,z)}{2\Delta{x}}
∂x∂m(x,y,z)=(Δxm(x+Δx,y,z)−m(x,y,z)+Δxm(x,y,z)−m(x−Δx,y,z))/2=2Δxm(x+Δx,y,z)−m(x−Δx,y,z),即对于矢量场中的每一个单元格来说,需要将其x方向的下一个单元格的矢量值减去上一个单元格的矢量值,最后将结果矢量值除以2倍的x方向的单元格尺寸,可以看到这种方式计算的当前单元格的偏导与自身的矢量值无关。
此时大部分人会有疑问:有限差分场非边缘位置的单元格的偏导按照中心差分求导法已经能手动算出来了,然而边缘位置的单元格在差分场中只有一个紧邻单元格,似乎无法使用中心差分求导法呢?实际上对于没有周期性边界条件的差分场来说,两侧的边缘位置的单元格则分别需要使用上述的前向差分和后向差分求导法,而对于存在周期性边界条件的差分场来说,边缘单元格在差分场之外也有紧邻的“扩展单元格”,“扩展单元格”的值为差分场之内对应周期位置的单元格的值,比如对于一个差分场分别存在非周期性边界条件和存在一维周期性边界条件(x方向)如下图所示:

图中绿色代表有限差分场的所有单元格,对x求偏导的过程中:对于没有周期性边界条件的差分场(上图),其左侧边缘的单元格(灰色方框)需要使用前向差分法求导;其右侧边缘的单元格(棕色方框)需要使用后向差分法求导;其内部的单元格则使用中心差分法求导。对于示例的具有一维周期性边界条件的差分场(下图),将该差分场沿周期方向进行左右平移一整个差分场,于是边缘单元格的差分场之外的紧邻扩展单元格的值便是对应的差分场之内的单元格的值,显然,对于类似这种具有周期性边界条件的差分场都需要使用中心差分法对所有单元格求导。
此外,也可以近似求解有限差分场的二阶偏导,即:
{
∂
2
m
→
(
x
,
y
,
z
)
∂
x
2
→
m
→
(
x
+
Δ
x
,
y
,
z
)
−
2
m
→
(
x
,
y
,
z
)
+
m
→
(
x
−
Δ
x
,
y
,
z
)
Δ
x
∂
2
m
→
(
x
,
y
,
z
)
∂
y
2
→
m
→
(
x
,
y
+
Δ
y
,
z
)
−
2
m
→
(
x
,
y
,
z
)
+
m
→
(
x
,
y
−
Δ
y
,
z
)
Δ
y
∂
2
m
→
(
x
,
y
,
z
)
∂
z
2
→
m
→
(
x
,
y
,
z
+
Δ
z
)
−
2
m
→
(
x
,
y
,
z
)
+
m
→
(
x
,
y
,
z
−
Δ
z
)
Δ
z
\begin{cases} \frac{\partial{^{2}\overrightarrow{m}(x,y,z)}}{\partial{x^2}} \rarr \frac{\overrightarrow{m}(x+\Delta{x},y,z) - 2\overrightarrow{m}(x,y,z)+\overrightarrow{m}(x-\Delta{x},y,z)}{\Delta{x}} \\\\ \frac{\partial{^{2}\overrightarrow{m}(x,y,z)}}{\partial{y^2}} \rarr \frac{\overrightarrow{m}(x,y+\Delta{y},z) - 2\overrightarrow{m}(x,y,z)+\overrightarrow{m}(x,y-\Delta{y},z)}{\Delta{y}} \\\\ \frac{\partial{^{2}\overrightarrow{m}(x,y,z)}}{\partial{z^2}} \rarr \frac{\overrightarrow{m}(x,y,z+\Delta{z}) - 2\overrightarrow{m}(x,y,z)+\overrightarrow{m}(x,y,z-\Delta{z})}{\Delta{z}} \end{cases}
⎩
⎨
⎧∂x2∂2m(x,y,z)→Δxm(x+Δx,y,z)−2m(x,y,z)+m(x−Δx,y,z)∂y2∂2m(x,y,z)→Δym(x,y+Δy,z)−2m(x,y,z)+m(x,y−Δy,z)∂z2∂2m(x,y,z)→Δzm(x,y,z+Δz)−2m(x,y,z)+m(x,y,z−Δz)
2.ubermag库函数验证
ubermag的discretisedfield类的 diff() 函数可以实现对有限差分场求导,这个函数可以被标量场和矢量场对象调用,并接受一个必要的求导方向参数字符串和一个可选的求导阶数参数。为了演示周期性边界条件对求导结果的影响,我们基于前文中没有周期性边界条件的“mag_skyrmion_t199_norm.omf”矢量场手动创建一个拥有x方向的周期性边界条件的矢量场,并保存为“mag_skyrmion_norm_PBC.omf”文件,接着对其求x方向的偏导,保存求导结果为“mag_PBC_diff_x.omf”文件:
#基于mag_skyrmion_t199_norm矢量场对象创建一个具有x方向的周期性边界条件的矢量场
#首先创建一个x方向的周期性网格
region = df.Region(p1=(0, 0, 0), p2=(150e-9, 50e-9, 2e-9))
mesh_PBC = df.Mesh(region=region, cell=(2e-9, 2e-9, 2e-9), bc="x")
#接着创建具有相同矢量值的矢量场
mag_skyrmion_norm_PBC = df.Field(mesh_PBC, nvdim=3, value=mag_skyrmion_t199_norm)
mag_skyrmion_norm_PBC.to_file("mag_skyrmion_norm_PBC.omf",representation="txt")
#对一维周期性边界条件的矢量场mag_skyrmion_PBC求偏导
mag_PBC_diff_x = mag_skyrmion_norm_PBC.diff("x")
mag_PBC_diff_x.to_file("mag_PBC_diff_x.omf",representation="txt")

从偏导结果场“mag_PBC_diff_x.omf”中挑选三个典型位置的单元格进行验证:①第一行的中间图显示了该矢量场的一个左边界单元格(1nm,17nm,1nm) 的偏导结果矢量值,通过在左侧图中获取其在矢量场中的紧邻单元格(3nm,17nm,1nm)的矢量值和对应周期的“扩展单元格”(149nm,17nm,1nm)的矢量值,右侧图给出了根据这两个单元格信息手动计算该左边界单元格的偏导结果。②矢量场内部的单元格(51nm,5nm,1nm)且存在一个紧邻单元格(49nm,5nm,1nm)的矢量值为(0,0,0),即第二行中间图中所标注的单元格,在左侧图中获取另一个紧邻单元格(53nm,5nm,1nm)的矢量值后,通过右侧图的手动计算检验了前文描述的计算流程。③第三行的中间图显示了一个该矢量场的一个右边界单元格(149nm,7nm,1nm)的偏导结果。以上的手动计算结果和调用ubermag库函数得到的结果完全相同,从而说明了需要使用中心差分求导法对存在周期性边界条件的有限差分场求偏导。
接下来,我们对没有周期性边界条件的“mag_skyrmion_t199_norm.omf”矢量场求x方向的偏导,保存求导结果为“mag_diff_x.omf”文件:
#对没有周期性边界条件的矢量场mag_skyrmion_t199_norm求偏导
mag_diff_x = mag_skyrmion_t199_norm.diff("x")
mag_skyrmion_t199_norm.to_file("mag_skyrmion_t199_norm.omf",representation="txt")
mag_diff_x.to_file("mag_diff_x.omf",representation="txt")

和前面周期性边界条件的矢量场的求导结果相比,该求导结果在两侧边界单元格发生了很明显的变化,同样从偏导结果场“mag_diff_x.omf.omf”中挑选三个典型位置的单元格进行验证:①第三行左图显示了矢量场内部的单元格(47nm,9nm,1nm)的矢量值为(0,0,0)和单元格(51nm,9nm,1nm)的非零矢量值,可以看到第三行右图手动计算单元格(49nm,9nm,1nm)的偏导结果和中间图的标注是一致的。然而,对于②第二行中间图标注的右边界单元格(149nm,9nm,1nm)和③第一行中间图标注的左边界单元格(1nm,29nm,1nm),从右图的分别手动计算后向差分和前向差分的结果来看,与库函数调用得到的中间图的结果在具体的数值上有一定的差异,这可能是因为库函数对边界单元格采用了精度更高的其他求导方法。

接下来,为 diff() 函数指定参数为 “order=2” 来近似求解有限差分场的二阶偏导:
#对没有周期性边界条件的矢量场mag_skyrmion_t199_norm求x方向的二阶偏导
mag_diff_x_2 = mag_skyrmion_t199_norm.diff("x",order=2)
mag_diff_x_2.to_file("mag_diff_x_2.omf",representation="txt")

右侧图只选取了一个典型的内部单元格(51nm,9nm,1nm)手动计算其x方向的二阶偏导,可以看到计算结果和使用库函数生成的“mag_diff_x_2.omf”中标注的结果完全相同。
3.标量场的梯度,矢量场的散度和旋度
有了前文有限差分场的代数计算和偏导的计算方法,那么可以轻易理解标量场的梯度,矢量场的散度和旋度计算方法。

Ⅰ 将矢量微分算子
∇
\nabla
∇与标量场进行相乘得到标量场的梯度(矢量场),比如求解组成矢量场
m
→
(
x
,
y
,
z
)
\overrightarrow{m}(x,y,z)
m(x,y,z)的x分量(标量场
m
x
m_x
mx)的梯度:
∇
m
x
(
x
,
y
,
z
)
=
(
∂
∂
x
,
∂
∂
y
,
∂
∂
z
)
m
x
=
(
∂
m
x
∂
x
,
∂
m
x
∂
y
,
∂
m
x
∂
z
)
\nabla{m_x(x,y,z)}=(\frac{\partial}{\partial{x}},\frac{\partial}{\partial{y}},\frac{\partial}{\partial{z}})m_x=(\frac{\partial{m_x}}{\partial{x}},\frac{\partial{m_x}}{\partial{y}},\frac{\partial{m_x}}{\partial{z}})
∇mx(x,y,z)=(∂x∂,∂y∂,∂z∂)mx=(∂x∂mx,∂y∂mx,∂z∂mx),即对于梯度结果矢量场中的每一个单元格
(
x
0
,
y
0
,
z
0
)
(x_0,y_0,z_0)
(x0,y0,z0)来说,其矢量值的x分量等于标量场
m
x
m_x
mx对x的偏导在该单元格的结果标量值,y分量等于标量场
m
x
m_x
mx对y的偏导在该单元格的结果标量值,z分量等于标量场
m
x
m_x
mx对z的偏导在该单元格的结果标量值。
我们直接利用ubermag的库函数 grad 计算矢量场“mag_skyrmion_t199_norm.omf”的x分量(标量场)的梯度,接着计算该标量场分别对x,y,z的偏导用来验证梯度计算结果:
#对矢量场mag_skyrmion_t199_norm的x分量(mx标量场)求梯度,结果为一个矢量场
mag_x_grad = mag_skyrmion_t199_norm.x.grad
mag_x_grad.to_file("mag_x_grad.omf",representation="txt")
#对矢量场mag_skyrmion_t199_norm的x分量(mx标量场)分别求x,y,z方向的偏导,用来验证梯度计算结果
mag_x_diff_x = mag_skyrmion_t199_norm.x.diff("x")
mag_x_diff_x.to_file("mag_x_diff_x.omf",representation="txt")
mag_x_diff_y = mag_skyrmion_t199_norm.x.diff("y")
mag_x_diff_y.to_file("mag_x_diff_y.omf",representation="txt")
mag_x_diff_z = mag_skyrmion_t199_norm.x.diff("z")
mag_x_diff_z.to_file("mag_x_diff_z.omf",representation="txt")

可以看到,左图中挑选的三个典型位置的单元格的矢量值的三个分量和右边三个图的标量值完全相同。此外,由于示例的有限差分场在z方向上只有一层单元格,所以对z的偏导结果始终为0。
Ⅱ 将矢量微分算子
∇
\nabla
∇与矢量场进行点积得到矢量场的散度(标量场),比如求解矢量场
m
→
(
x
,
y
,
z
)
\overrightarrow{m}(x,y,z)
m(x,y,z)的散度:
∇
⋅
m
→
(
x
,
y
,
z
)
=
(
∂
∂
x
,
∂
∂
y
,
∂
∂
z
)
⋅
(
m
x
,
m
y
,
m
z
)
=
∂
m
x
∂
x
+
∂
m
y
∂
y
+
∂
m
z
∂
z
\nabla \cdot \overrightarrow{m}(x,y,z)=(\frac{\partial}{\partial{x}},\frac{\partial}{\partial{y}},\frac{\partial}{\partial{z}})\cdot{(m_x,m_y,m_z)}=\frac{\partial{m_x}}{\partial{x}}+\frac{\partial{m_y}}{\partial{y}}+\frac{\partial{m_z}}{\partial{z}}
∇⋅m(x,y,z)=(∂x∂,∂y∂,∂z∂)⋅(mx,my,mz)=∂x∂mx+∂y∂my+∂z∂mz,即对于散度结果标量场中的每一个单元格
(
x
0
,
y
0
,
z
0
)
(x_0,y_0,z_0)
(x0,y0,z0)来说,其标量值等于标量场
m
x
m_x
mx对x的偏导在该单元格的结果标量值 + 标量场
m
y
m_y
my对y的偏导在该单元格的结果标量值 + 标量场
m
z
m_z
mz对z的偏导在该单元格的结果标量值。
我们使用库函数 div 计算矢量场“mag_skyrmion_t199_norm.omf” 的散度,接着分别计算组成该矢量场的三个标量场对三个方向的偏导:
#对矢量场mag_skyrmion_t199_norm求散度,结果为一个标量场
mag_skyrmion_div = mag_skyrmion_t199_norm.div
mag_skyrmion_div.to_file("mag_skyrmion_div.omf",representation="txt")
#对矢量场mag_skyrmion_t199_norm的x分量(mx标量场)求x方向的偏导,用来验证散度计算结果
mag_x_diff_x = mag_skyrmion_t199_norm.x.diff("x")
mag_x_diff_x.to_file("mag_x_diff_x.omf",representation="txt")
#对矢量场mag_skyrmion_t199_norm的y分量(my标量场)求y方向的偏导
mag_y_diff_y = mag_skyrmion_t199_norm.y.diff("y")
mag_y_diff_y.to_file("mag_y_diff_y.omf",representation="txt")
#对矢量场mag_skyrmion_t199_norm的z分量(mz标量场)求z方向的偏导
mag_z_diff_z = mag_skyrmion_t199_norm.z.diff("z")
mag_z_diff_z.to_file("mag_z_diff_z.omf",representation="txt")

从散度结果标量场“mag_skyrmion_div.omf” (左图)选择一个典型的单元格进行手动计算,从右图可以看到该单元格的标量值正是由三个标量场分别求偏导后的标量值相加的结果。
Ⅲ 将矢量微分算子
∇
\nabla
∇与矢量场进行叉积得到矢量场的旋度,比如求解矢量场
m
→
(
x
,
y
,
z
)
\overrightarrow{m}(x,y,z)
m(x,y,z)的旋度:
∇
×
m
(
x
,
y
,
z
)
=
(
∂
∂
x
,
∂
∂
y
,
∂
∂
z
)
×
(
m
x
,
m
y
,
m
z
)
=
(
∂
m
z
∂
y
−
∂
m
y
∂
z
,
∂
m
x
∂
z
−
∂
m
z
∂
x
,
∂
m
y
∂
x
−
∂
m
x
∂
y
)
\nabla \times m(x,y,z)=(\frac{\partial}{\partial{x}},\frac{\partial}{\partial{y}},\frac{\partial}{\partial{z}})\times{(m_x,m_y,m_z)}=(\frac{\partial{m_z}}{\partial{y}}-\frac{\partial{m_y}}{\partial{z}},\frac{\partial{m_x}}{\partial{z}}-\frac{\partial{m_z}}{\partial{x}},\frac{\partial{m_y}}{\partial{x}}-\frac{\partial{m_x}}{\partial{y}})
∇×m(x,y,z)=(∂x∂,∂y∂,∂z∂)×(mx,my,mz)=(∂y∂mz−∂z∂my,∂z∂mx−∂x∂mz,∂x∂my−∂y∂mx),有了上文的铺垫,很容易求解
m
→
\overrightarrow{m}
m的旋度场中每一个单元格的矢量值的三个分量,即:x分量等于
m
→
\overrightarrow{m}
m的z分量标量场对y求偏导的标量结果 值 -
m
→
\overrightarrow{m}
m的y分量标量场对z求偏导的标量结果值;y分量等于,,,
有了前文的计算示例,我们使用库函数 curl 计算矢量场“mag_skyrmion_t199_norm.omf” 的旋度,接着便根据上式直接使用库函数计算组成旋度场的三个标量场结果:
#对矢量场mag_skyrmion_t199_norm求旋度,结果为一个矢量场
mag_skyrmion_curl = mag_skyrmion_t199_norm.curl
mag_skyrmion_curl.to_file("mag_skyrmion_curl.omf",representation="txt")
#根据旋度公式分别计算旋度场的三个分量场
#计算旋度场的x分量
mag_skyrmion_curl_x = mag_skyrmion_t199_norm.z.diff("y") - mag_skyrmion_t199_norm.y.diff("z")
mag_skyrmion_curl_x.to_file("mag_skyrmion_curl_x.omf",representation="txt")
#计算旋度场的y分量
mag_skyrmion_curl_y = mag_skyrmion_t199_norm.x.diff("z") - mag_skyrmion_t199_norm.z.diff("x")
mag_skyrmion_curl_y.to_file("mag_skyrmion_curl_y.omf",representation="txt")
#计算旋度场的z分量
mag_skyrmion_curl_z = mag_skyrmion_t199_norm.y.diff("x") - mag_skyrmion_t199_norm.x.diff("y")
mag_skyrmion_curl_z.to_file("mag_skyrmion_curl_z.omf",representation="txt")

可以很清楚的看到左图旋度场中标注的典型单元格的矢量值的三个分量与右图标量场在这些单元格的标量值是一一对应关系,和前文旋度公式的描述是一致的。
理解了上述的三种计算流程,那么对标量场或矢量场的拉普拉斯计算则是触类旁通的,使用ubermag的库函数 laplace 即可,该函数可以被一个标量场对象或矢量场对象调用。本文则不再演示其计算流程。

三、积分运算
1.手动计算流程
在阅读一些文章的时候,我们经常从方程中看到对有限差分场的xy平面进行面积分,或者对整个有限差分场进行体积分,相比前文描述的求导,有限差分场的积分则简单的多。对有限差分场的面积分
∬
f
i
e
l
d
(
x
,
y
,
z
)
d
S
\iint field(x,y,z)dS
∬field(x,y,z)dS进行离散化之前,需要先选择一个需要积分的平面,比如
f
i
e
l
d
(
x
,
y
,
z
)
field(x,y,z)
field(x,y,z)在z方向有多层单元格,那么通过“z=N”就能限定对第N层的xy平面进行面积分:
∬
f
i
e
l
d
(
x
,
y
,
z
=
N
)
d
S
⟹
∑
i
,
j
∈
S
f
i
e
l
d
(
x
i
,
y
j
,
z
N
)
⋅
Δ
S
=
f
i
e
l
d
(
x
0
,
y
0
,
z
N
)
⋅
Δ
S
+
f
i
e
l
d
(
x
1
,
y
0
,
z
N
)
⋅
Δ
S
+
.
.
.
\iint field(x,y,z=N)dS \implies \displaystyle\sum_{i,j\in{S}}{field(x_i,y_j,z_N) \cdot \Delta{S}}={field(x_0,y_0,z_N)}\cdot \Delta{S}+{field(x_1,y_0,z_N)}\cdot \Delta{S}+...
∬field(x,y,z=N)dS⟹i,j∈S∑field(xi,yj,zN)⋅ΔS=field(x0,y0,zN)⋅ΔS+field(x1,y0,zN)⋅ΔS+...
其中
Δ
S
=
Δ
x
⋅
Δ
y
\Delta{S}=\Delta{x}\cdot\Delta{y}
ΔS=Δx⋅Δy为单元格在该平面的两个方向上的长度乘积,即面积。通过遍历该平面的所有单元格,将每一个单元格的场值乘以单元格的面积,并将所有乘积相加的结果便是有限差分场对该平面的面积分结果值(标量场的面积分得到一个标量值结果,矢量场的面积分得到一个矢量值结果)。
对有限差分场的体积分
∭
f
i
e
l
d
(
x
,
y
,
z
)
d
V
\iiint field(x,y,z)dV
∭field(x,y,z)dV进行离散化:
∭
f
i
e
l
d
(
x
,
y
,
z
)
d
V
⟹
∑
i
,
j
,
k
∈
V
f
i
e
l
d
(
x
i
,
y
j
,
z
k
)
⋅
Δ
V
=
f
i
e
l
d
(
x
0
,
y
0
,
z
0
)
⋅
Δ
V
+
f
i
e
l
d
(
x
1
,
y
0
,
z
0
)
⋅
Δ
V
+
.
.
.
\iiint field(x,y,z)dV \implies \displaystyle\sum_{i,j,k\in{V}}{field(x_i,y_j,z_k) \cdot \Delta{V}}={field(x_0,y_0,z_0)}\cdot \Delta{V}+{field(x_1,y_0,z_0)}\cdot \Delta{V}+...
∭field(x,y,z)dV⟹i,j,k∈V∑field(xi,yj,zk)⋅ΔV=field(x0,y0,z0)⋅ΔV+field(x1,y0,z0)⋅ΔV+...
其中
Δ
V
=
Δ
x
⋅
Δ
y
⋅
Δ
z
\Delta{V}=\Delta{x}\cdot\Delta{y}\cdot\Delta{z}
ΔV=Δx⋅Δy⋅Δz为单元格的三个方向上的长度乘积,即单元格的体积。通过遍历有限差分场中所有单元格,将每一个单元格的场值乘以单元格的体积,并将所有乘积相加的结果便是有限差分场的体积分结果值(标量场的体积分得到一个标量值结果,矢量场的体积分得到一个矢量值结果)。通过对比面积分的离散形式可以发现,体积分的乘积项比面积分多了一个某方向的单元格数量乘以单元格尺寸(即整个差分场在某一方向的长度),所以将面积分的结果乘以差分场在平面法向方向的长度便是体积分的结果。
2.ubermag库函数验证
描述斯格明子的拓扑电荷的方程为: Q = 1 4 π ∬ ( ∂ m → ∂ x × ∂ m → ∂ y ) ⋅ m → d x d y Q=\frac{1}{4\pi}\iint (\frac{\partial{\overrightarrow m}}{\partial{x}} \times \frac{\partial{\overrightarrow m}}{\partial{y}}) \cdot {\overrightarrow m}\quad dxdy Q=4π1∬(∂x∂m×∂y∂m)⋅mdxdy,对于面积分内部的被积项,我们通过前文的学习已经能够轻易的求解得到一个标量场结果,接着使用ubermag的库函数 integrate() 选择对某一个xy平面进行面积分。这里仍然使用前文的“mag_skyrmion_t199_norm.omf”矢量场作为示例,由于该矢量场在z方向仅有一层单元格,所以直接选择该默认的xy平面进行面积分:
import math
#计算面积分的内部被积项:mag_skyrmion_t199_norm对x的偏导叉积对y的偏导,并点积自身
integrate_inner = (mag_skyrmion_t199_norm.diff("x").cross(mag_skyrmion_t199_norm.diff("y"))).dot(mag_skyrmion_t199_norm)
integrate_inner.to_file("integrate_inner.omf",representation="txt")
#由于integrate_inner在z方向只有一层单元格,所以直接选择默认的xy平面
integrate_surface = integrate_inner.sel("z").integrate()
print(f"{integrate_surface=}") #integrate_surface=array([-10.546097])
#计算拓扑电荷Q值
Q_value = integrate_surface/(4*math.pi)
print(f"{Q_value=}") #Q_value=array([-0.83923173])
将内部被积项“integrate_inner.omf”标量场文件的后缀名改为txt,并直接拖进origin的工作表中,删去注释信息后对其进行列统计并得到该数据列(标量场)的总和,接着将总和乘以单元格的面积 Δ S = Δ x ⋅ Δ y = 2 e − 9 × 2 e − 9 \Delta{S}=\Delta{x}\cdot\Delta{y}=2e-9 \times 2e-9 ΔS=Δx⋅Δy=2e−9×2e−9,最后除以 4 π 4\pi 4π得到Q值:

可以看到手动计算面积分并求Q值的结果与库函数输出结果“Q_value=array([-0.83923173]”相同。
当 integrate() 函数直接被差分场对象调用时(即没有使用 sel() 函数选择平面),则表示对差分场进行体积分。这里直接对“integrate_inner”标量场进行体积分,即:
#计算体积分
integrate_volume = integrate_inner.integrate()
print(f"{integrate_volume=}") #integrate_volume=array([-2.1092194e-08])
#验证体积分的结果时面积分的结果乘以差分场在z方向的长度
z_length = integrate_volume / integrate_surface
print(f"{z_length=}") #z_length=array([2.e-09])
输出结果“z_length=array([2.e-09])”与预期相符,即将体积分的结果除以面积分的结果便是差分场在该平面法线方向(z)的总长度。
总结
本文结合ubermag的库函数介绍了关于有限差分场数值计算的各种手动计算流程,需要注意ubermag官网更新比较频繁,很多库函数的名称可能随着版本变化发生巨大变化,自己使用时注意去网站的“changelog”页面看一下函数名称是否发生变化。
最后,值此2023年终末之时,2024年伊始之际,祝大家新年胜旧年,将来胜过往,在新的一年里能心想事成,万事如意!