GAN的实现
上一篇文章中我们说到了GAN的数学解释
min
G
max
D
V
(
D
,
G
)
=
E
x
∼
p
data
(
x
)
[
log
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
=
−
log
4
+
2
J
S
D
(
p
data
∥
p
g
)
≥
−
log
4
,
where
[
p
d
a
t
a
=
p
g
]
\min_{G} \max_{D} V(D, G) = \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_{z}(z)}[\log(1 - D(G(z)))]\\ = -\log 4 + 2JSD(p_{\text{data}} \parallel p_g)\\ \geq -\log 4, \quad \text{where } [p_{data} = p_g]
GminDmaxV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]=−log4+2JSD(pdata∥pg)≥−log4,where [pdata=pg]
- Pratically: 𝒑𝒈 → 𝒑𝒅𝒂𝒕𝒂
- Question: Can we make 𝒑𝒈 → 𝒑𝒅𝒂𝒕𝒂 where we have 𝑫∗ ?
下面补充一下GAN的伪代码
Pseudo Code

上面这段伪码先训练鉴别器(Discriminator, D)k次,再训练生成器(Generator, G)。
对于每次训练迭代:
- 对于鉴别器
D,进行 k 次更新:- 从噪声先验 p_g(z) 中采样 m 个噪声样本 {z^1, …, z^m} 。
- 从数据生成分布 ( p_{data}(x) ) 中采样 m 个样本 {x^1, …, x^m}。
- 使用上升的随机梯度更新鉴别器
D(即最大化 log(D(x)) 和 log(1-D(G(z)))) 。
- 更新生成器
G:- 再次从噪声先验中采样 m 个噪声样本。
- 使用下降的随机梯度更新生成器
G(即最小化 log(1-D(G(z))))。
Q1: 为什么是上升和下降(ascending & descending)?
A1: 这是因为在GAN的框架中,鉴别器D的目标是最大化它正确分类真实和生成样本的能力,这可以通过最大化 log(D(x)) 和 log(1-D(G(z))) 来实现,这被称为上升(ascending)。相反,生成器G的目标是最小化鉴别器D正确识别其生成的样本的能力,这可以通过最小化 log(1-D(G(z))) 来实现,这被称为下降(descending)。
Q2: 生成器
G的更新有什么问题吗?
A2: 当 D(G(z)) 趋向于0(即在开始时,鉴别器D很容易识别出生成的样本是假的),log(1-D(G(z))) 的梯度会消失,这会使得生成器G的训练变得非常缓慢。为了解决这个问题,可以使用 -log(D(G(z))) 来代替 log(1-D(G(z))),因为前者在 D(G(z)) 小的时候梯度较大,有利于生成器G的训练。这实际上就是将假图的label置为了1。
Wasserstein GAN
WGAN是一种改进的GAN,旨在解决原始GAN训练中的一些问题,如梯度消失和模式崩溃。
WGAN I——“破”
还记得我们上一篇文章最后提到的那个还有点严重的问题吗?2017年的一篇论文彻底说破了这个问题的原因。
下面我们一步一步来说
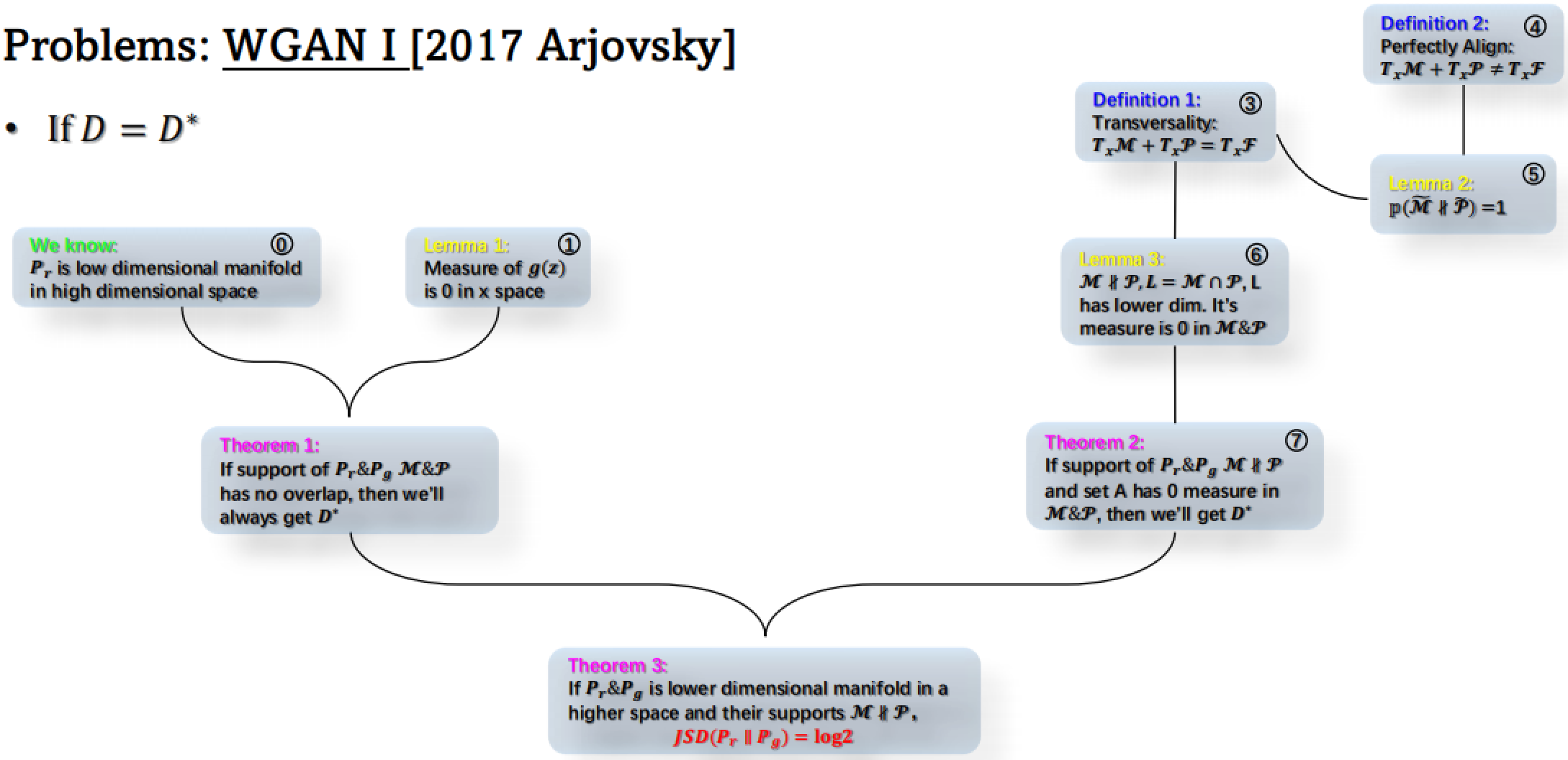
如果鉴别器 ( D ) 达到最优 ( D* ),那么:
- 已知:⓪ 真实数据分布 ( Pr ) 是高维空间中的低维流形。
- 流形(Manifold)指的是一个局部具有欧几里得空间性质的空间,即在小的尺度上,每一点都有一个邻域与欧几里得空间同胚(即连续可逆且逆函数也连续),但在整体上可能具有复杂的结构,这意味着它可能会弯曲或扭曲。
- 高维空间中的低维流形是指嵌入在高维空间中的、但本身维度较低的流形。
- 一个简单的例子是地球表面:虽然地球表面是三维空间中的一个对象,但任何给定的地方都可以近似为二维平面——这就是地球表面可以被视为一个二维流形的原因。
- 在机器学习中,高维空间中的低维流形概念特别重要,因为数据往往存在于高维空间**(例如,图像像素空间)**,而这些数据实际上可能位于一个相对低维的流形上。这意味着虽然数据点在高维空间中分布,但它们实际上可能受到更低维度的基础结构的约束。
- 引理1:① 生成器的输出 g(z) 在 x 空间中的测度为 0。
- **测度(Measure)**用于精确地描述集合的“大小”。
- 在直观上,你可以将测度理解为一个集合的“体积”。对于一维空间(如实数线),测度就类似于“长度”;对于二维空间(如平面),测度类似于“面积”;对于三维空间,测度类似于“体积”。在高维空间中,测度概念仍然适用,尽管可能无法直观地理解为常规的几何体积。
- 生成器的输出 g(z) 在 x 空间中的测度为 0 时,这是在说从生成器输出的数据集在目标空间中占据了极其“稀疏”的区域。换句话说,尽管 x 空间可能是一个非常高维的空间(例如,一张图片的所有像素构成的空间),生成器输出的图像集合可以被嵌入到这个空间的一个低维子空间中,这个子空间相对于整个 x 空间来说几乎没有“体积”。
- 或者这样理解——将一个二维平面“升维”,从三维去看这个平面,那么总会至少找到一个角度“看不到”这个平面。
- 因为生成器输入的是低维的随机噪声 z,并且生成器是一个连续的函数,因此它的输出 g(z) 形成的是一个低维流形。这个流形在高维的 x 空间中只覆盖了一个极其小的区域,从测度的角度来看几乎是 0。
- **测度(Measure)**用于精确地描述集合的“大小”。
- 定理1:② 如果真实数据分布 Pr 和生成数据分布 Pg 的支撑集(support)互不重叠,那么鉴别器总能达到最优(D*)。
- 分布与分布之间可能分离、相交或相切,这里互不重叠指的就是分离。

-
定义1(Transversality):③ 两个流形的切空间之和等于目标空间的切空间(即分布相交的情况)。
- 具体来说,如果两个流形在交点处的切空间直和起来能够“跨越”整个目标空间,则它们在该点是横截的。
- 举一个简单的例子:想象在三维空间中有两条线(1维流形)。如果这两条线在某一点相交,且它们的切线在该点不共线,那么这两条线在该点是横截的,因为它们的切线(即它们的切空间)跨越了整个三维空间。换句话说,你可以使用这两条线在交点处的切线来生成三维空间中任意方向的一个向量。
- 在定义1中,如果我们有两个流形 M 和 P,并且它们在某一点 x 处相交,那么横截性要求在 x 点的流形 M 的切空间 TxM 加上流形 P 的切空间 TxP 应该等于包含它们的目标空间 F 在 x 点的切空间 TxF。这意味着 M 和 P 在 x 点处的交集是以一种非退化的方式相交的,从而它们的局部结构能够完全覆盖整个目标空间的局部结构。
-
定义2(Perfectly Align):④ 两个流形的切空间之和不等于目标空间的切空间(即分布相切的情况)。
- 这里的相切其实有4种情况
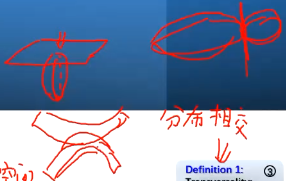
- 这里的相切其实有4种情况
-
引理2:⑤ 如果两个分布的支撑集完美对齐,则它们的交集的概率为1。
- 相切情况的存在非常不稳定,所以实际上只有相离和相交两种情况。
-
引理3:⑥ 如果 M 和 Pr 的交集是 M 和 Pg 的交集的低维流形,那么这个交集在 M 和 Pg 中的测度为0。
-
定理2:⑦ 如果 Pr 和 Pg 的支撑集相交,且交集的测度为0,那么鉴别器也能达到最优。
-
定理3:⑧ 如果 Pr 和 Pg 这两个分布是高维空间中的低维流形,并且它们的支撑集在 M 和 Pg 中有交集,且这个交集的测度为0,那么Jensen-Shannon Divergence(JSD)就会等于 log2。
- log2 的推导如下

- log2 的推导如下
至此,我们发现在最优判别器D*的情况下,JSD的值应该会是log2。
min
G
max
D
V
(
D
,
G
)
=
E
x
∼
p
data
(
x
)
[
log
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
=
−
log
4
+
2
J
S
D
(
p
data
∥
p
g
)
≥
−
log
4
,
where
[
p
d
a
t
a
=
p
g
]
\begin{align} \min_{G} \max_{D} V(D, G) &= \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_{z}(z)}[\log(1 - D(G(z)))]\\ &= -\log 4 + 2JSD(p_{\text{data}} \parallel p_g)\\ &\geq -\log 4, \quad \text{where } [p_{data} = p_g] \end{align}
GminDmaxV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]=−log4+2JSD(pdata∥pg)≥−log4,where [pdata=pg]
然而,还记得我们最开始的想法吗?**我们希望通过p_data = p_g,使得JSD = 0,从而取到minmax函数的最小值-log4。**现在的事实却是——minmax永远取不到最小值-log4而只能取到0,因为如果需要最优判别器完美分别两个分布,此时的JSD会等于log2而不是0。
重新梳理一下:
问题的核心在于,当鉴别器
D达到其最优状态D*时,是否可以使生成器的分布 P_g 完全匹配真实数据的分布P_data。However,在积分中带入0我们发现
对于生成器的目标函数 f(G) ,如果鉴别器是完美的(即 P_data = P_g ),那么 JS散度(JSD)应该是0,并且 f(G) 应该是 -log4 。然而,如果 P_data 和 P_g 完全不相交(即完全不重叠),JSD会是 log2 ,导致 f(G) = 0 。
这意味着,**如果鉴别器达到最优,我们不会有任何梯度(即“没有损失”)**来指导生成器的训练。换句话说,最优的鉴别器将无法提供有关如何改进生成器的有用信息,因为它会对所有的生成样本都给出相同的响应,导致生成器无法从鉴别器的反馈中学习(随着D越来越好,G会越来越差)。
这个矛盾从原理上解释了为什么我们之前用原始GAN生成的质量这么差,因为在一段时间后它根本就没有学任何东西。
这里可能有人会有疑问:D*是一个理想状态,为什么能说明整个学习的过程质量差呢?
其实这里作者还补充了以下两种情况的数学推导
-
当采用原始公式

- 定理4表明,如果鉴别器 D 非常接近最优鉴别器 D*,并且生成器的梯度有界,那么鉴别器对生成器的梯度的范数将是有界的。这意味着,当 D 接近 D* 时,生成器的更新梯度将变得非常小。
- 从而引出推论1,当 D 与 D* 的差距趋于0时,鉴别器对生成器的梯度将趋向于0,导致梯度消失。
-
当采用愚弄法(将假图的label置为了1)

- 发现1:这里经过定理5数学推导,计算得到式子后半部分变成了两个距离相减(KL-JS)。在训练过程中,我们希望梯度更大从而来获得更好的更新,这就意味着KL向↑而JS向↓。可是KL和JS都是在描述 P_g 到 P_data 的距离,它们的训练方向产生了矛盾。
- 发现2:KL散度是P_g 相对于 P_data 的非对称测度。当 P_g 接近于 P_data 时,KL散度接近于0;而当两者差别很大时,KL散度会趋向于无穷大。如果 P_g 完全不同于 P_data,那么 KL(P_g∥P_data) 会非常大,导致训练困难,也就是模式坍塌。也就是说,如果生成的图像比较新颖,会遭受巨大惩罚,这也正是我们之前在MNIST手写数字时遇到那个奇怪问题的原因(生成了很多一样的东西)—— 系统被鼓励生成那些已经成功了的东西,失去了创新能力。
总之,原始GAN的两种方法都存在问题。
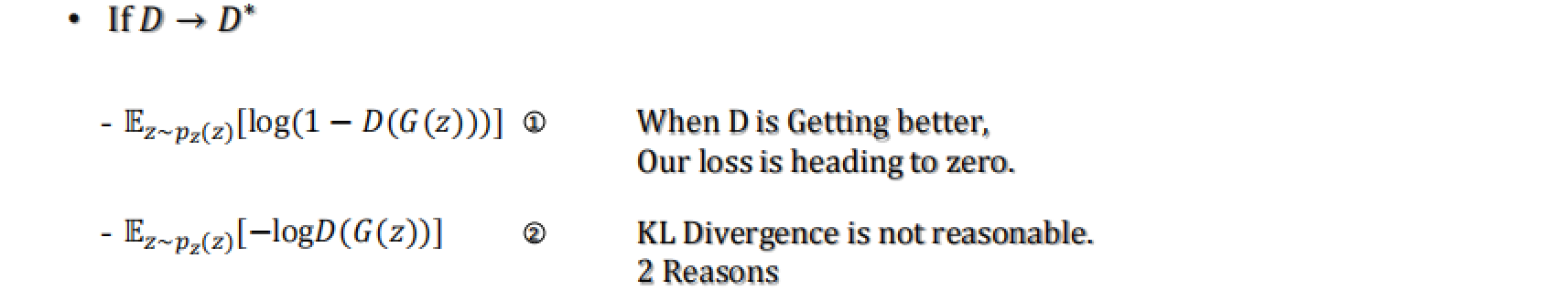
WGAN II——“立”
Wasserstein Distance
俗话说不破不立,Arjovsky 不光将GAN的“旧世界”给“破”了,还在他的第二篇论文中“立”了一个“新世界”——WGAN(Wasserstein Distance)。
“Wasserstein”其实是德语里的一个复合词,由“Wasser”(水)和“Stein”(石头)组成。

从结果反推过程,原始GAN的损失函数由于JS距离而出现了问题。因此,Wasserstein GAN通过使用不同的损失函数(即Wasserstein距离)解决了JSD=log2的问题,从而即使在最优鉴别器D*的情况下也能够提供有效的梯度给生成器。
我们先来看看Wasserstein Distance的公式
W
(
P
r
,
P
g
)
=
inf
γ
∈
Π
(
P
r
,
P
g
)
E
(
x
,
y
)
∼
γ
[
∥
x
−
y
∥
]
W(P_r, P_g) = \inf_{\gamma \in \Pi(P_r, P_g)} \mathbb{E}_{(x,y)\sim \gamma} [\|x - y\|]
W(Pr,Pg)=γ∈Π(Pr,Pg)infE(x,y)∼γ[∥x−y∥]
inf表示下确界,寻找使得期望值最小的联合分布γ。
E_{(x,y)~γ}表示对于联合分布γ下的随机变量(x, y)的期望值。
[|x - y|]是x和y之间的范数,通常是欧几里得距离。
我们还是拆成几部分来看
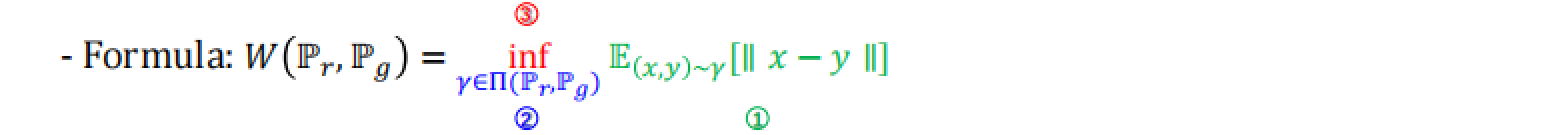
① 其中,
E
(
x
,
y
)
∼
γ
[
∥
x
−
y
∥
]
=
∫
y
∫
x
γ
(
x
,
y
)
∥
x
−
y
∥
d
x
d
y
=
∑
x
,
y
∥
x
−
y
∥
γ
(
x
,
y
)
\mathbb{E}_{(x,y)\sim \gamma} [\|x - y\|] = \int_{y}\int_{x} \gamma(x,y) \|x - y\| \,dx\,dy = \sum_{x,y} \|x - y\| \gamma(x,y)
E(x,y)∼γ[∥x−y∥]=∫y∫xγ(x,y)∥x−y∥dxdy=x,y∑∥x−y∥γ(x,y)
我们应该时刻牢记Wasserstein Distance的目标——算出Pr和Pg之间的距离,所以很容易理解公式中的(x, y) 可以分别对应为左下角图片的Pr和Pg(每根柱子就是x1,x2,x3,…,y1,y2,y3…)
这样一来||x - y||其实就是一个距离矩阵(每根柱子与另一分布的每个柱子作差)
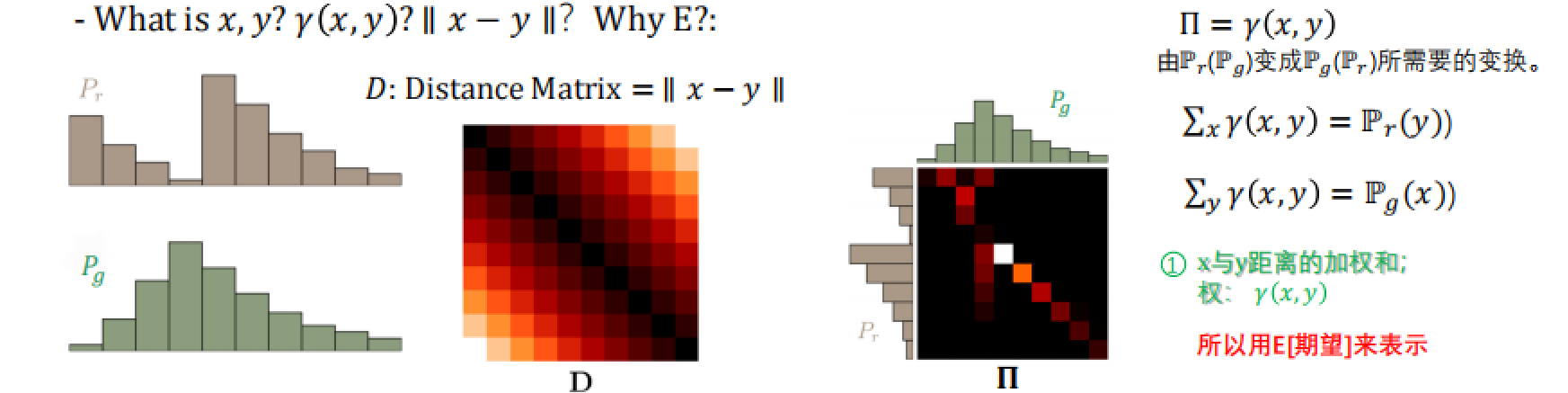
接下来看到第3张图(也是最重要的一张),它揭示了“我需要做出什么样的努力才能使Pg变成Pr,或者Pr变成Pg”,即什么是γ(x,y)。
明确几个概念:
-
在这张热力图中,亮度较高的点表示在联合分布
Π中具有较高的概率密度,这意味着在最优运输问题中,从真实分布 Pr 到生成分布 Pg 的特定值转移概率质量的可能性较大。比如 Pr 中第1行的亮点位于 Pg 的第2和第4列,表明这部分概率质量主要被转移到了这两个位置。原因可能是:
- 生成模型(Pg)在这些位置有较高的概率质量,这表示生成分布在这些值上有更多的质量,所以在这些点处需要从 Pr 转移更多的质量过来以匹配 Pg。
- 成本较低,这可能表明从 Pr 的这一特定值转移到 Pg 的第2和第4列的成本(即距离)较低,因此在优化运输计划时,这些转移被优先考虑。
相反,如果某些点很暗,甚至是黑色,这意味着在这些
(x, y)对上几乎没有概率质量被转移。原因反之同上。
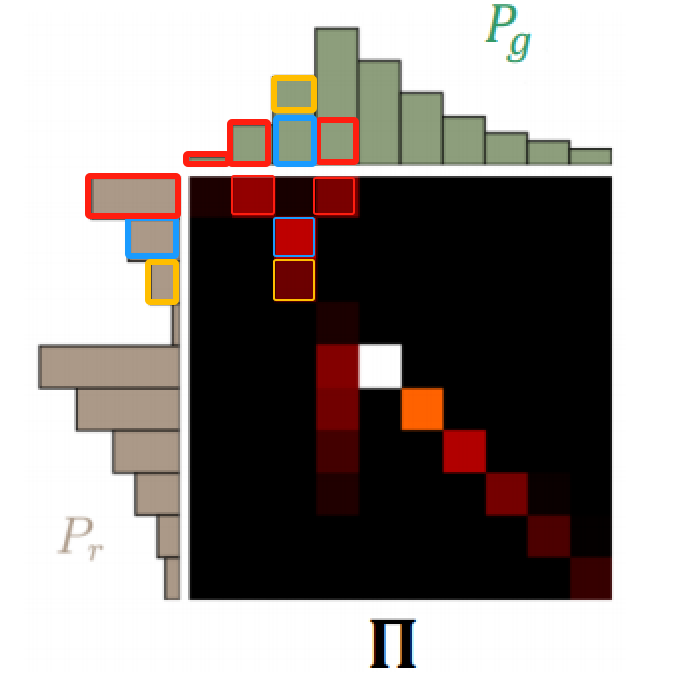
-
在热力图中,每个亮点代表了一个
(x, y)对,而|x - y|就是这对之间的距离或成本。γ(x, y)是这对的联合概率,所以||x - y||·γ(x,y)实际上代表了从 Pr 到 Pg 的概率质量转移的“强度”或“成本”。因此,整个公式就是计算在所有可能的
(x, y)对上,将质量从x移动到y的期望成本。
总结一下:|x - y|是分布移动的“距离”,γ(x,y)是分布移动的“量”,两者相乘就是我们移动的“工作量”。我们的目的是让这个“工作量”尽可能小(如果你看懂了上面的概念就会知道,Wasserstein的转移方法可能会有无穷多种,具体如何找最小是一个找全局最优解的过程,下面会进行数学推导)。
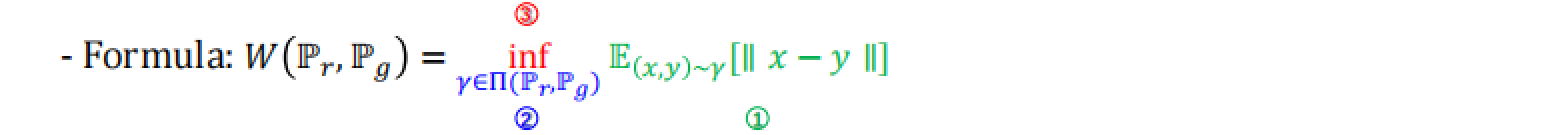
②③在上面也已经顺带解释过了——Π包含了所有可能的 (x, y)对,我们的目标是找到一个全局最优解

Lipschitz
展示的是Wasserstein距离 W(Pr, Pg) 的几种等价定义,这些定义来自于数学中的对偶性原理。这里涉及的是Kantorovich-Rubinstein对偶性,它允许我们从最优运输问题的原问题(primal problem)转化为其对偶问题(dual problem)。
-
原问题:最初的问题是寻找最小化运输成本的运输计划,即找到使得期望运输成本最小的联合分布
γ,这表达为
i n f γ ∈ Π ( P r , P g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] inf_{\gamma \in \Pi(P_r, P_g)} E_{(x,y)\sim\gamma} [\|x - y\|] infγ∈Π(Pr,Pg)E(x,y)∼γ[∥x−y∥] -
对偶问题:通过对偶性原理,我们可以将这个最小化问题转换为一个最大化问题。对偶问题寻找的是满足1-Lipschitz条件的函数集合上的一个最大值,这个条件意味着这些函数的梯度(或者在离散情况下的差分)被限制在1以内。这些函数
f被称为1-Lipschitz函数,因为它们的斜率(在任意两点之间的斜率)被限制在±1的范围内。 -
Lipschitz条件:Lipschitz条件是数学中对函数斜率的一种约束,具体来说,如果一个函数是K-Lipschitz的,那么对于所有的
x1和x2,有|f(x1) - f(x2)| <= K * |x1 - x2|。在Wasserstein距离的背景下,我们通常关注1-Lipschitz函数,即K=1。
这种从最小化到最大化的转变反映了我们可以从寻找实际的运输计划(计算成本)转变为寻找一个函数,该函数能够“衡量”两个分布之间的差异。这个函数在所有可能的情况下给出的期望值差异是最大的,而且这个函数满足Lipschitz条件。因此,在数学上,寻找最优运输计划的最小值问题转化为了寻找衡量分布之间差异的函数的最大值问题。这两个问题在数学上是等价的。
W
(
P
r
,
P
g
)
=
inf
γ
∈
Π
(
P
r
,
P
g
)
E
(
x
,
y
)
∼
γ
[
∥
x
−
y
∥
]
=
sup
∥
f
∥
L
≤
1
E
x
∼
P
r
[
f
(
x
)
]
−
E
x
∼
P
g
[
f
(
x
)
]
=
max
w
∈
W
E
x
∼
P
r
[
f
w
(
x
)
]
−
E
z
∼
P
z
[
f
w
(
g
θ
(
z
)
)
]
\begin{align} W(P_r, P_g) &= \inf_{\gamma \in \Pi(P_r, P_g)} \mathbb{E}_{(x,y)\sim\gamma} [\|x - y\|] \\ &= \sup_{\|f\|_L\leq 1} \mathbb{E}_{x\sim P_r}[f(x)] - \mathbb{E}_{x\sim P_g}[f(x)] \\ &= \max_{w\in W} \mathbb{E}_{x\sim P_r} [f_w(x)] - \mathbb{E}_{z\sim P_z} [f_w(g_\theta(z))] \end{align}
W(Pr,Pg)=γ∈Π(Pr,Pg)infE(x,y)∼γ[∥x−y∥]=∥f∥L≤1supEx∼Pr[f(x)]−Ex∼Pg[f(x)]=w∈WmaxEx∼Pr[fw(x)]−Ez∼Pz[fw(gθ(z))]
最后一个等式是在生成对抗网络(GAN)中的对应。这里 fw 通是判别器网络,gθ 是生成器网络,z 是来自先验分布 Pz 的噪声变量。在GAN的背景下,实际上就是在最大化这个期望值差异相当于训练判别器以最大程度地区分真实数据分布 Pr 和生成数据分布 Pg。
至此,来看一下WGAN的伪代码

两个要点:
-
将真图和假图分别送入D,然后会得到一个值,相减做一个L1-Loss即可,然后我们回传这个loss去训练D。
-
为了满足Lipschitz条件(才能满足Kantorovich-Rubinstein对偶性),这里直接对
w进行了硬截断。
WGAN代码实战
# dataset: mnist
import argparse
import os
import numpy as np
import math
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch
from generator import Generator
from discriminator import Discriminator
os.makedirs("images_wgan", exist_ok=True)
parser = argparse.ArgumentParser()
parser.add_argument("--n_epochs", type=int, default=200, help="number of epochs of training")
parser.add_argument("--batch_size", type=int, default=64, help="size of the batches")
parser.add_argument("--lr", type=float, default=0.00005, help="learning rate")
parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation")
parser.add_argument("--latent_dim", type=int, default=100, help="dimensionality of the latent space")
parser.add_argument("--img_size", type=int, default=28, help="size of each image dimension")
parser.add_argument("--channels", type=int, default=1, help="number of image channels")
parser.add_argument("--n_critic", type=int, default=5, help="number of training steps for discriminator per iter")
parser.add_argument("--clip_value", type=float, default=0.01, help="lower and upper clip value for disc. weights")
parser.add_argument("--sample_interval", type=int, default=400, help="interval betwen image samples")
opt = parser.parse_args()
print(opt)
img_shape = (opt.channels, opt.img_size, opt.img_size)
cuda = True if torch.cuda.is_available() else False
# Initialize generator and discriminator
generator = Generator()
discriminator = Discriminator()
if cuda:
generator.cuda()
discriminator.cuda()
# Configure data loader
os.makedirs("./data/mnist", exist_ok=True)
dataloader = torch.utils.data.DataLoader(
datasets.MNIST(
"./data/mnist",
train=True,
download=True,
transform=transforms.Compose(
[transforms.Resize(opt.img_size),
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5])] # [] means channel, 0.5,0.5 means mean & std
# => img = (img - mean) / 0.5 per channel
),
),
batch_size=opt.batch_size,
shuffle=True,
)
# Optimizers
optimizer_G = torch.optim.RMSprop(generator.parameters(), lr=opt.lr)
optimizer_D = torch.optim.RMSprop(discriminator.parameters(), lr=opt.lr)
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
# ----------
# Training
# ----------
batches_done = 0
for epoch in range(opt.n_epochs):
for i, (imgs, _) in enumerate(dataloader):
# Configure input
real_imgs = imgs.type(Tensor)
# ---------------------
# Train Discriminator
# ---------------------
optimizer_D.zero_grad()
# Sample noise as generator input
z = Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim)))
# Generate a batch of images
fake_imgs = generator(z).detach()
# Adversarial loss: 原始GAN使用的是交叉熵损失函数,而WGAN使用的是Wasserstein损失
loss_D = -torch.mean(discriminator(real_imgs)) + torch.mean(discriminator(fake_imgs)) # 真实图片的判别器输出的负均值+生成图片的判别器输出的均值
loss_D.backward()
optimizer_D.step()
# Clip weights of discriminator: 为了满足Lipschitz约束(函数的梯度必须小于等于1),需要对判别器的权重进行剪辑,以确保它们位于一个固定的很小的区间内
for p in discriminator.parameters():
p.data.clamp_(-opt.clip_value, opt.clip_value)
# Train the generator every n_critic iterations
if i % opt.n_critic == 0:
# -----------------
# Train Generator
# -----------------
optimizer_G.zero_grad()
# Generate a batch of images
gen_imgs = generator(z)
# Adversarial loss
loss_G = -torch.mean(discriminator(gen_imgs))
loss_G.backward()
optimizer_G.step()
print(
"[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
% (
epoch, opt.n_epochs, batches_done % len(dataloader), len(dataloader), loss_D.item(), loss_G.item())
)
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)
batches_done += 1
训练策略(Training Strategy):
- 在WGAN中,判别器(在WGAN中通常称为critic)需要比生成器更频繁地更新,以更准确地评估Wasserstein距离。这段代码通过参数
opt.n_critic控制,即每训练n_critic次判别器之后,才训练一次生成器。 - 这种策略有助于稳定训练过程,确保判别器不会太快地超过生成器,从而使得两者能够更有效地学习。
最后生成结果

可以看到每个数字都不一样了,即便是生成错误的也是不一样的错误。对比一下原始GAN的生成结果

而且WGAN还顺便解决了生成图像存在噪声(noise)这一问题。
以上就是WGAN作者Arjovsky 的两篇论文,对于原始GAN的先“破”后“立”。但是你以为这就完了吗?NoNo,Arjovsky 认为他在第二篇文章中“立”的新世界并不完美,于是便又发表了第三篇文章——WGAN III。欲知后事如何,请听下回分解~