牛顿-莱布尼茨公式
牛顿-莱布尼茨公式是微积分中的基本定理之一,它描述了函数的导数和不定积分之间的关系。
该公式通常用来计算定积分。设函数f(x)在区间[a, b]上连续,且F(x)是f(x)在该区间上的一个原函数
即F’(x) = f(x)。则牛顿-莱布尼茨公式表示为:
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
\int_{a}^{b} f(x) \,dx = F(b) - F(a)
∫abf(x)dx=F(b)−F(a)
这个公式描述的就是 F(b)-F(a) , 等于下方的面积
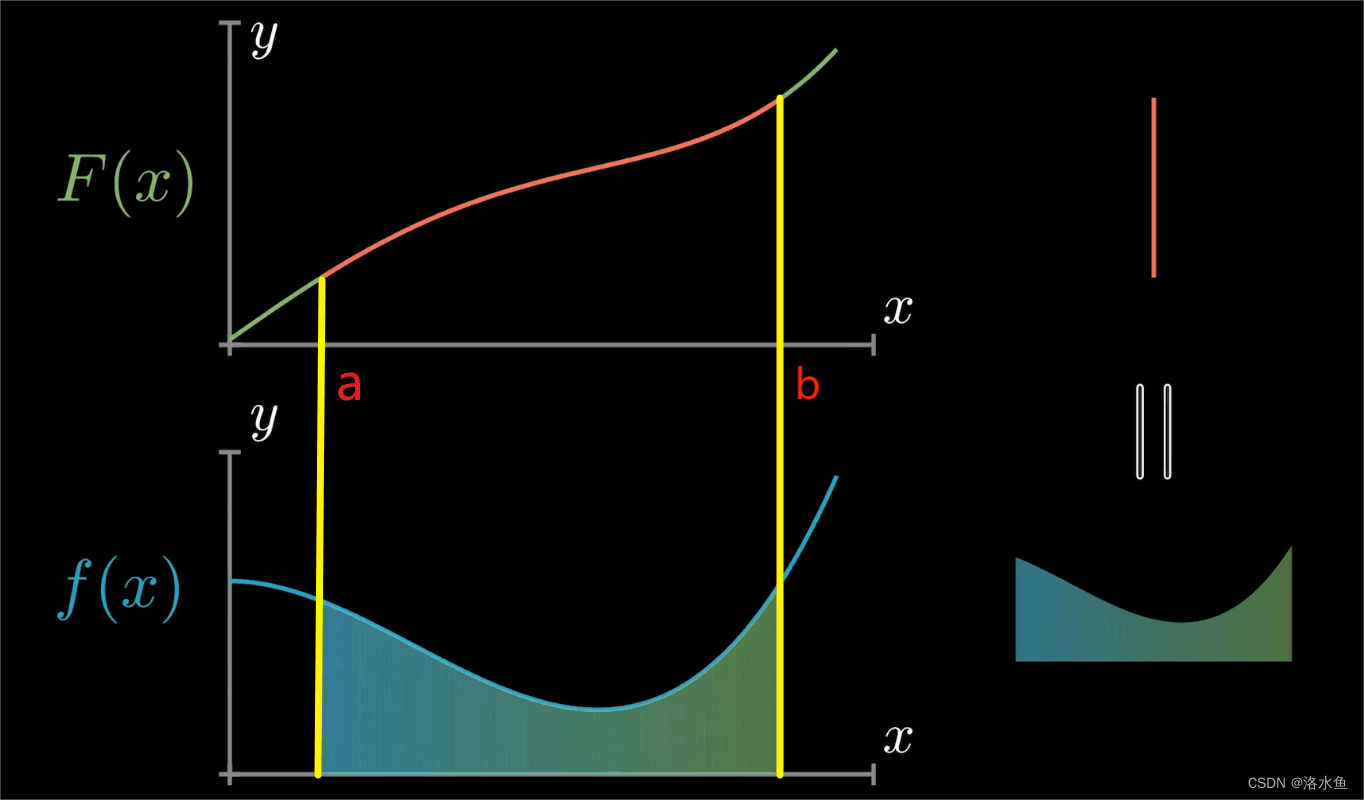
下面开始证明:
第一步 F(x)与f(x)联系
任意在F(X) 上找段变化的区域,如下图:
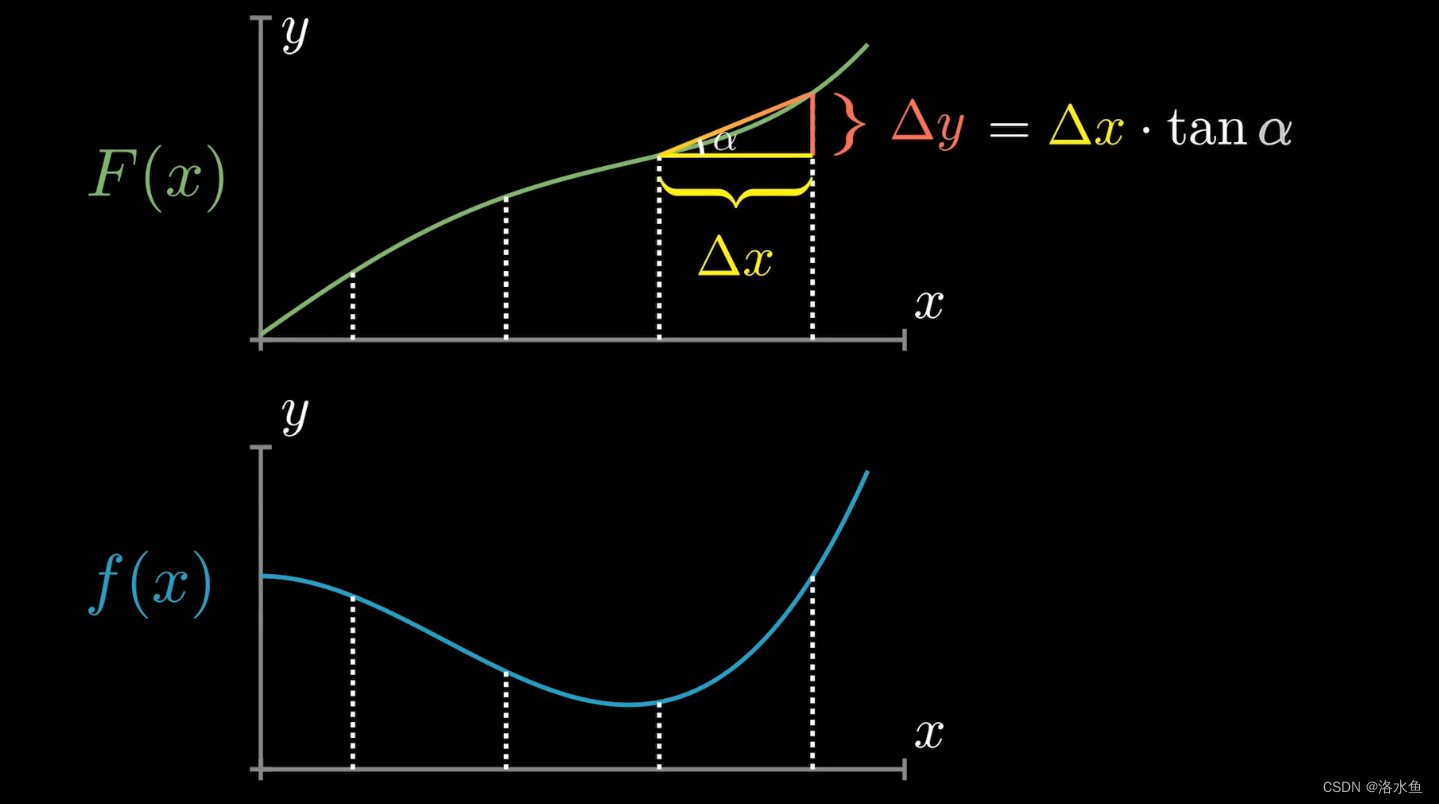
由拉格朗日中值定理得:
△
(
x
)
区域上必然有一个点切线的斜率等于
tan
(
α
)
\bigtriangleup(x) \hspace{0.5cm}区域上必然有一个点切线的斜率等于 \hspace{0.5cm}\tan(\alpha)
△(x)区域上必然有一个点切线的斜率等于tan(α)
所以可以得出 △ ( y ) = △ ( x ) ∗ f ( n ) \bigtriangleup(y) = \bigtriangleup(x)*f(n) △(y)=△(x)∗f(n)
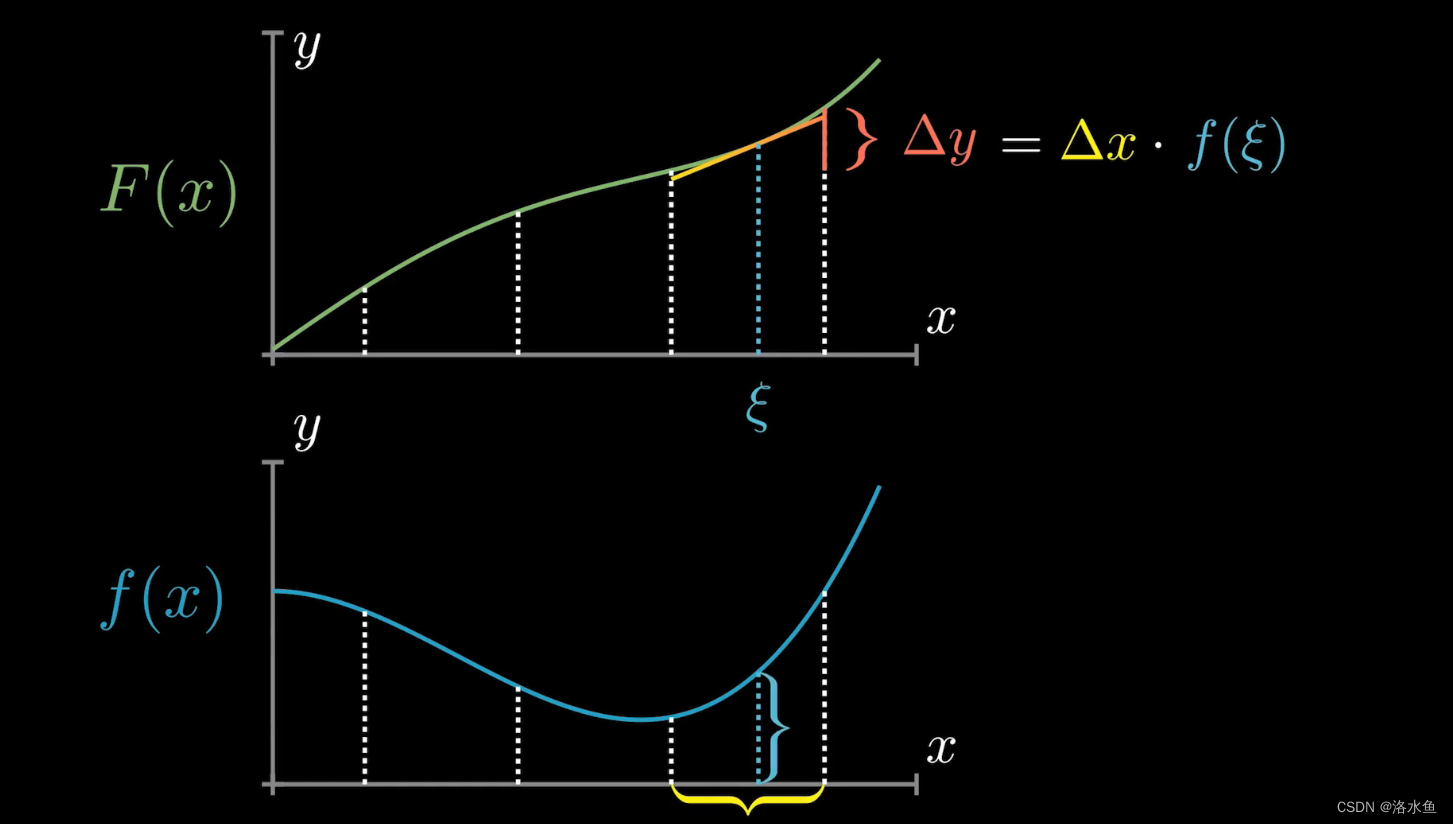
所以有下图:
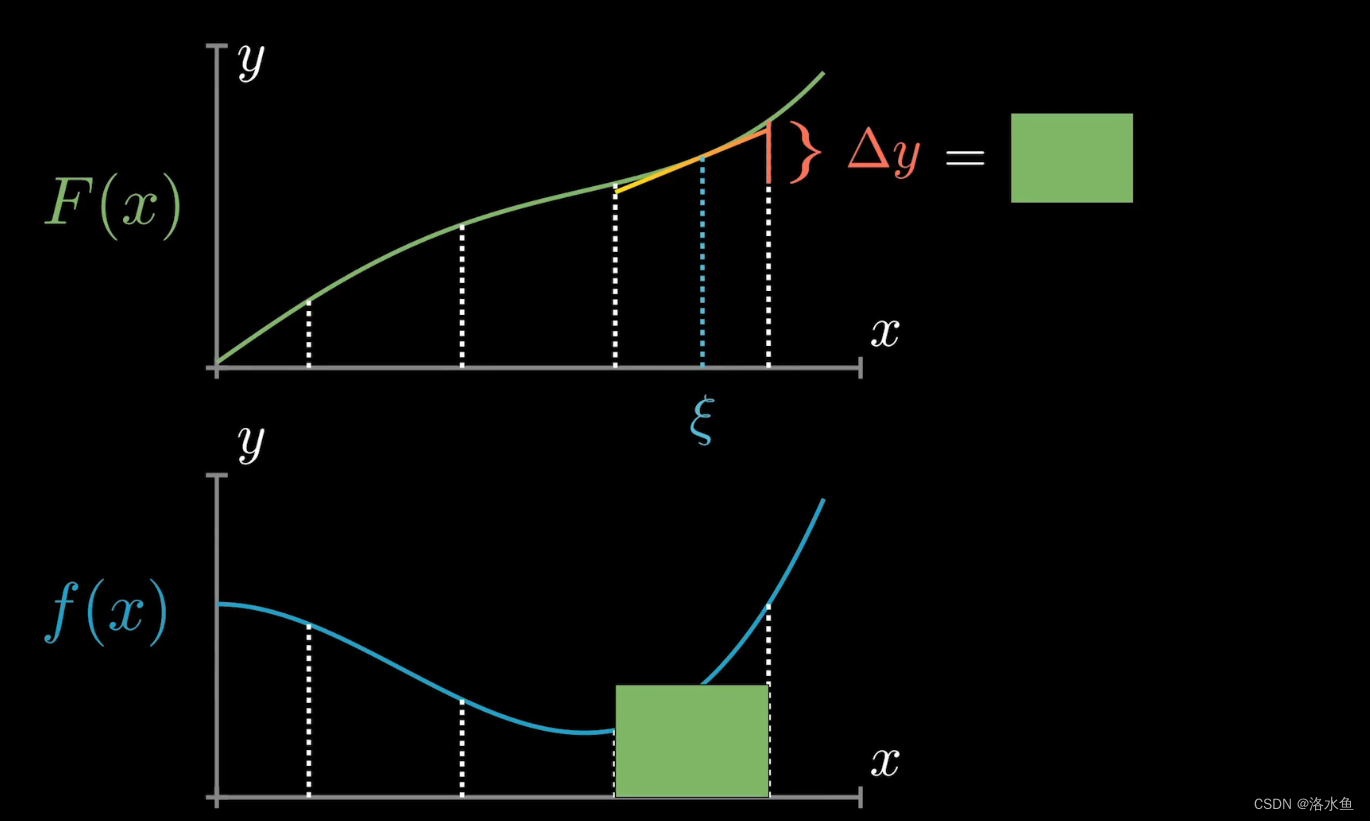
当我们取更多的
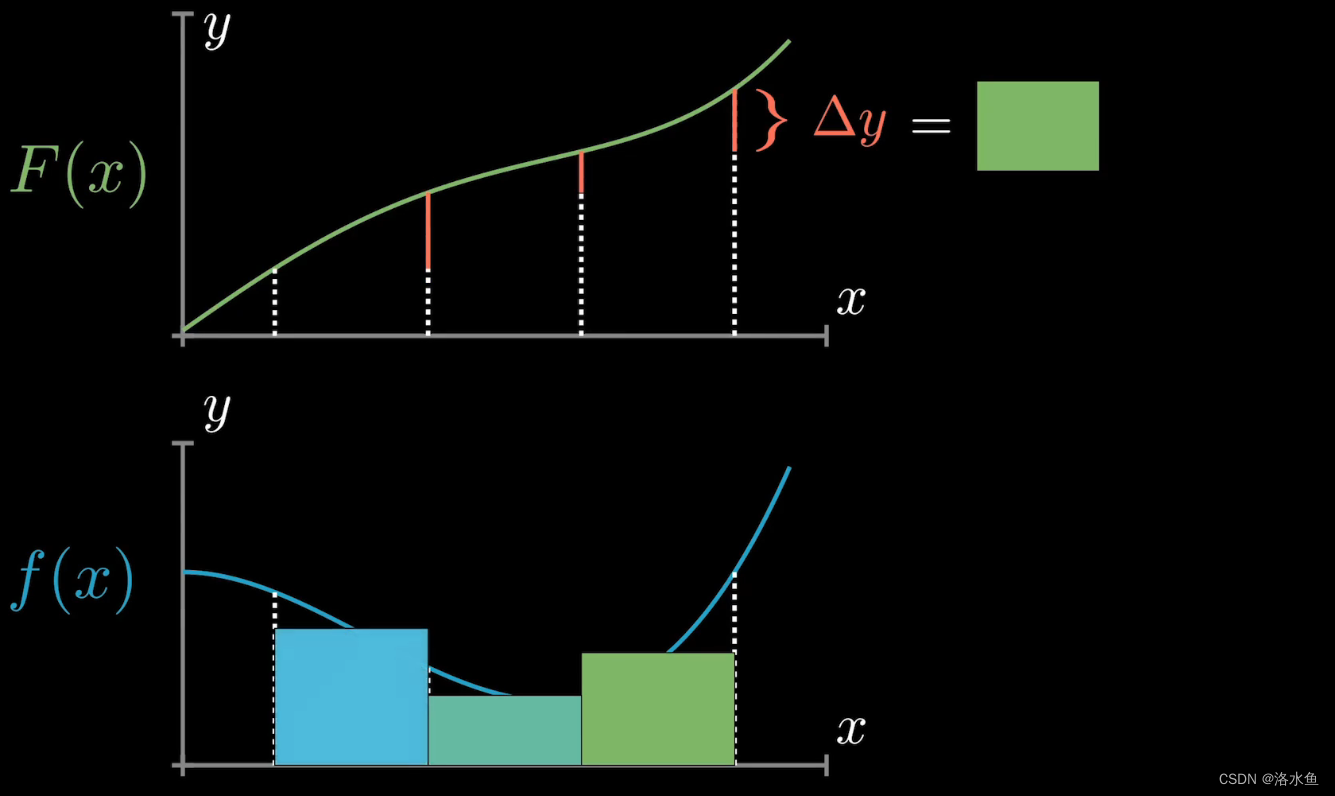
但这显然还没有证完
第二步 取的更密
取的更密之后,我们发现面积的组成,越来越解决贴合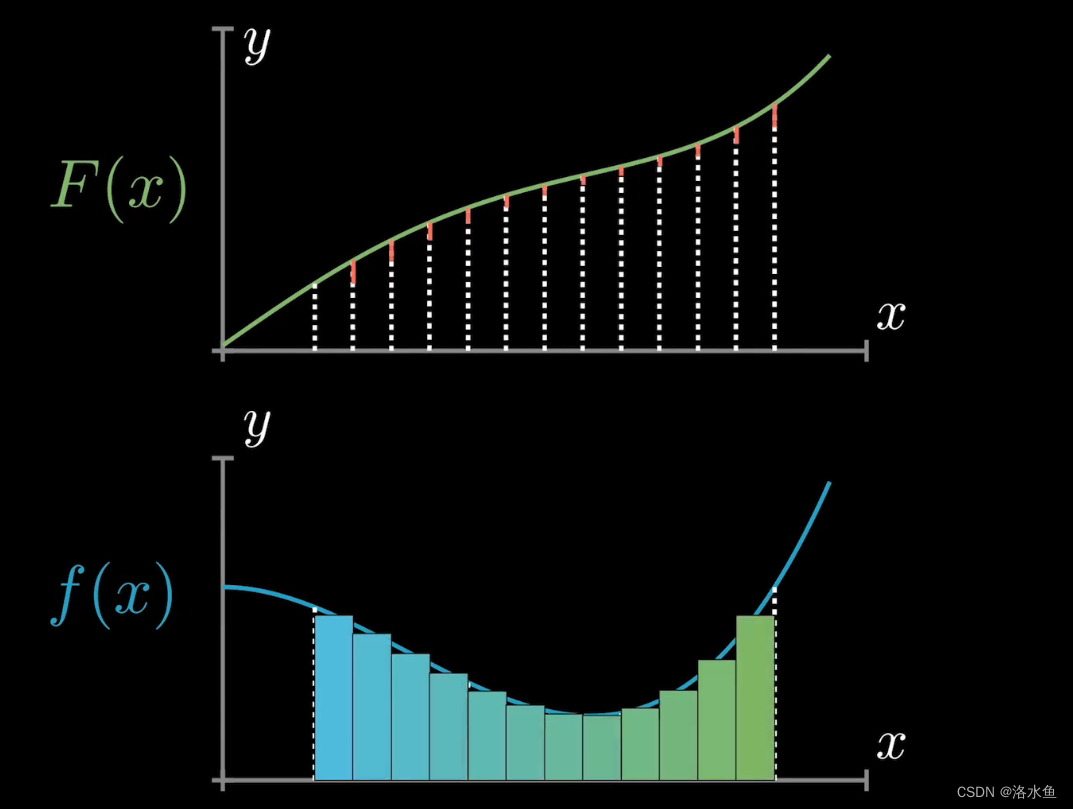
所以我们就可以在其中取无数的点,让其直接贴合
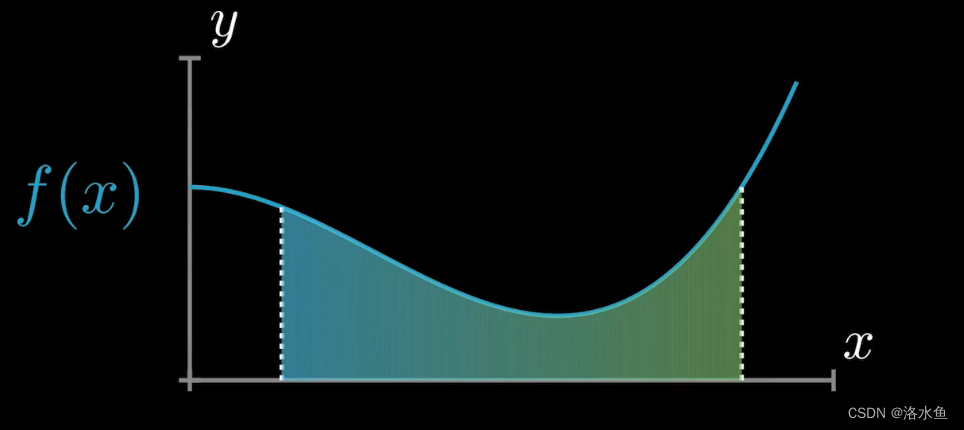
那我们怎么把这么多的面积和表示为这个呢
?
∫
a
b
f
(
x
)
d
x
那我们怎么把这么多的面积和表示为这个呢?\\ \int_{a}^{b} f(x) \,dx
那我们怎么把这么多的面积和表示为这个呢?∫abf(x)dx
对变化量
△
(
x
)
,
△
(
y
)
都任意大小的拆为
n
份
,
然后显然展开得下图
:
对变化量\bigtriangleup(x),\bigtriangleup(y)都任意大小的拆为n份,然后显然展开得下图:
对变化量△(x),△(y)都任意大小的拆为n份,然后显然展开得下图:

最后通过黎曼和可以推出
F
(
b
)
−
F
(
a
)
=
∫
a
b
f
(
x
)
d
x
F(b) - F(a) = \int_{a}^{b} f(x) \,dx
F(b)−F(a)=∫abf(x)dx
使用定理:
拉格朗日中值定理
黎曼和
参考视频B站