1、引入
- 二叉树的遍历
递归实现的方式:
public static class Node {
public int value;
Node left;
Node right;
public Node(int data) {
this.value = data;
}
}
//每个节点都是被有限次访问,时间复杂度O(N),因为每次递归都要存储返回信息,N为树的节点个数,
//递归使用了系统栈,额外空间复杂度为树的高度
public static void process(Node root) {
if (root == null) return ;
//1. 如果在此处打印 root.value 是先序遍历
//print(root.value);
process(root.left);
//2. 如果在此处打印root.value,是中序遍历
process(root.right;
//3. 如果在此处打印root.value,是后序遍历
}
非递归方式实现的时候依然要使用栈(自己实现的栈),额外空间复杂度还是树的高度。
也就是说无论是递归还是非递归方式遍历二叉树,树的高度这个额外空间是省不了的。
2、Morris简介
Morris遍历是一种遍历二叉树的方式,且时间复杂度为 O ( N ) O(N) O(N),额外空间复杂度为 O ( 1 ) O(1) O(1)。
通过利用原树中大量空闲指针的方式,达到节省空间的目的。
3、Morris 遍历的细节
假设来到当前节点 cur,开始时 cur 来到头节点位置
-
如果
cur没有左孩子,cur向右移动(cur = cur.right) -
如果
cur有左孩子,找到左子树上最右的节点mostRight:
a. 如果mostRight的右指针指向空,让其指向cur,然后cur向左移动(cur = cur.left)
b. 如果mostRight的右指针指向cur,让其指向null,然后cur向右移动(cur = cur.right) -
cur为空时遍历停止
举例:
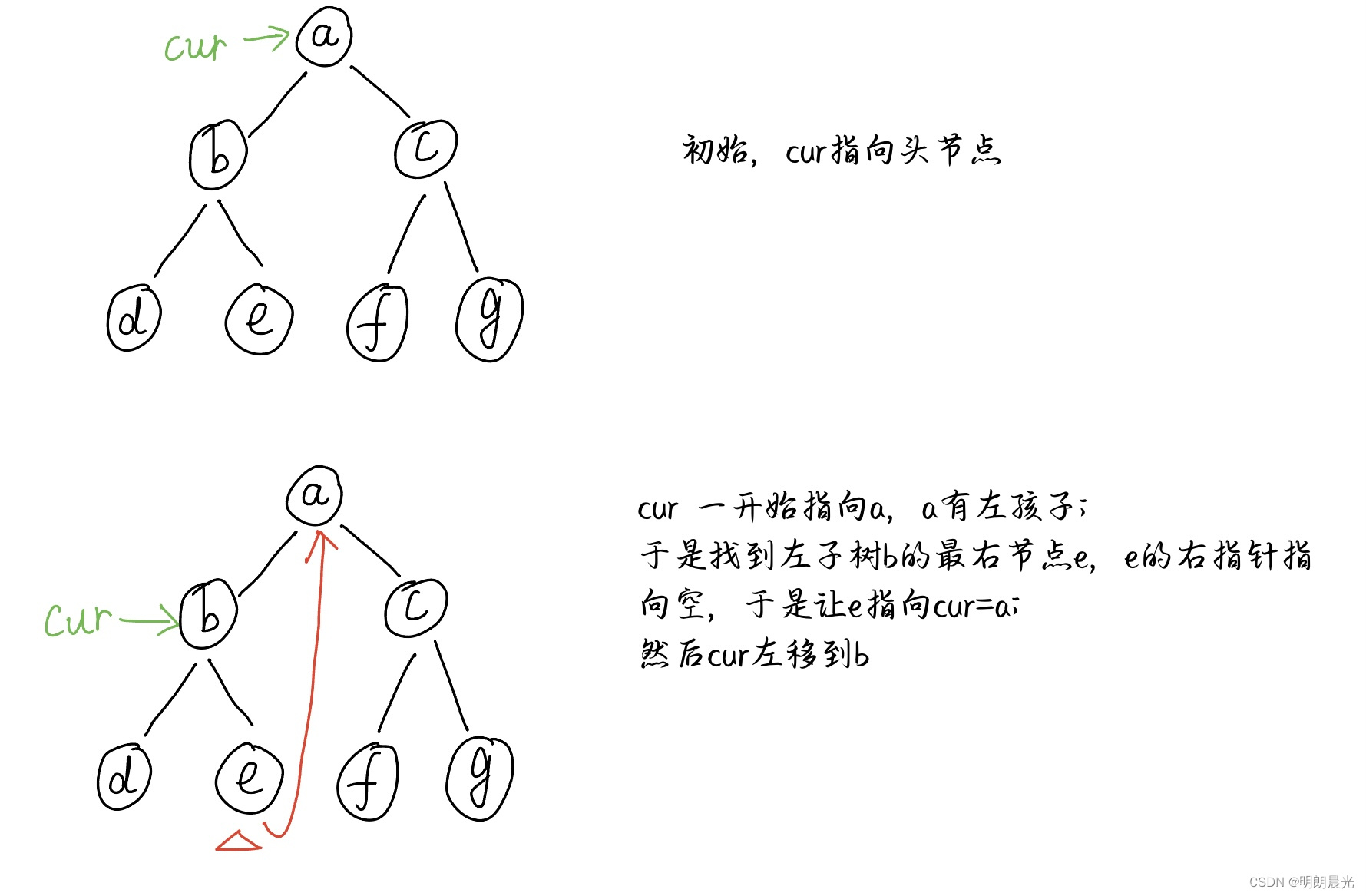
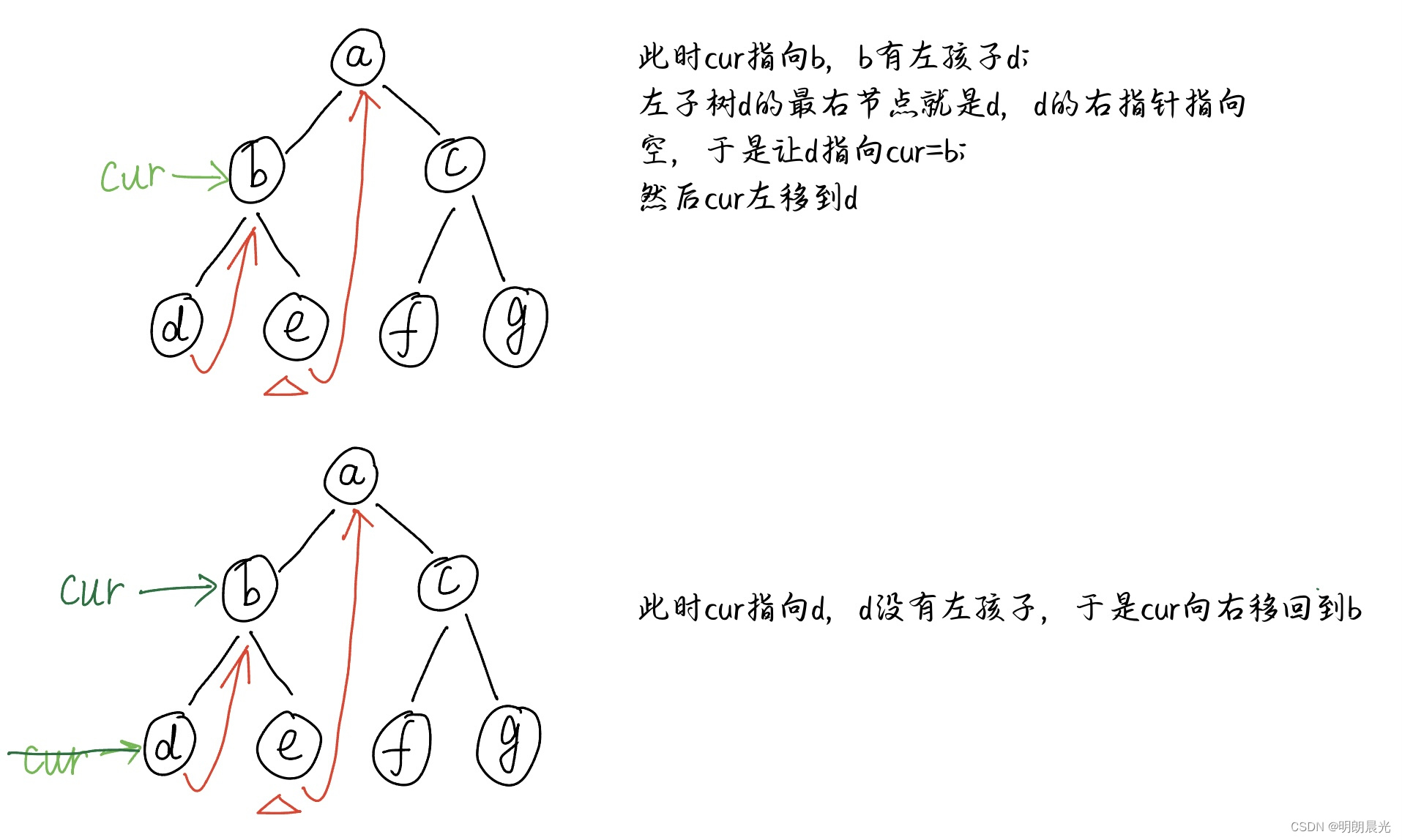
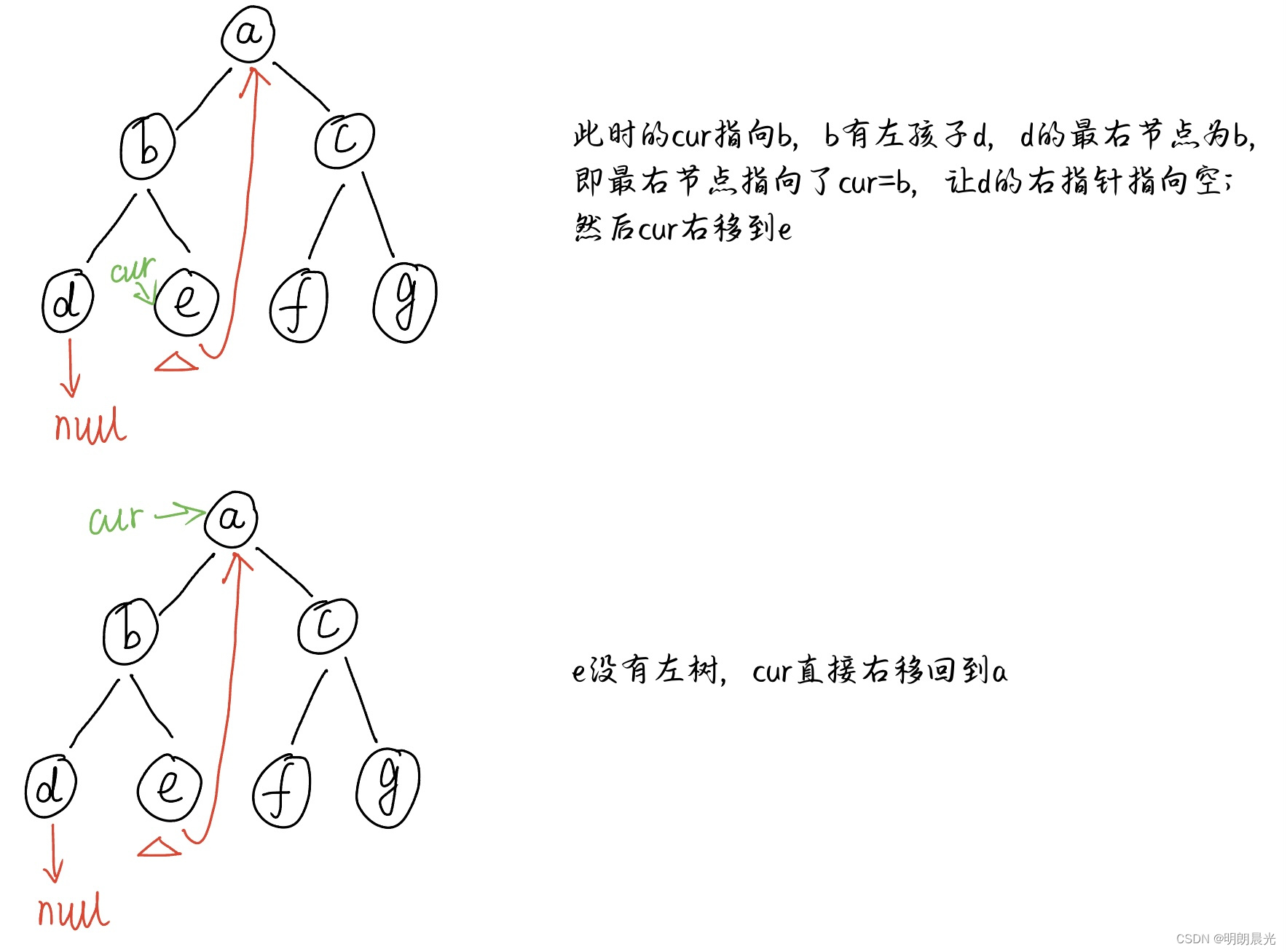
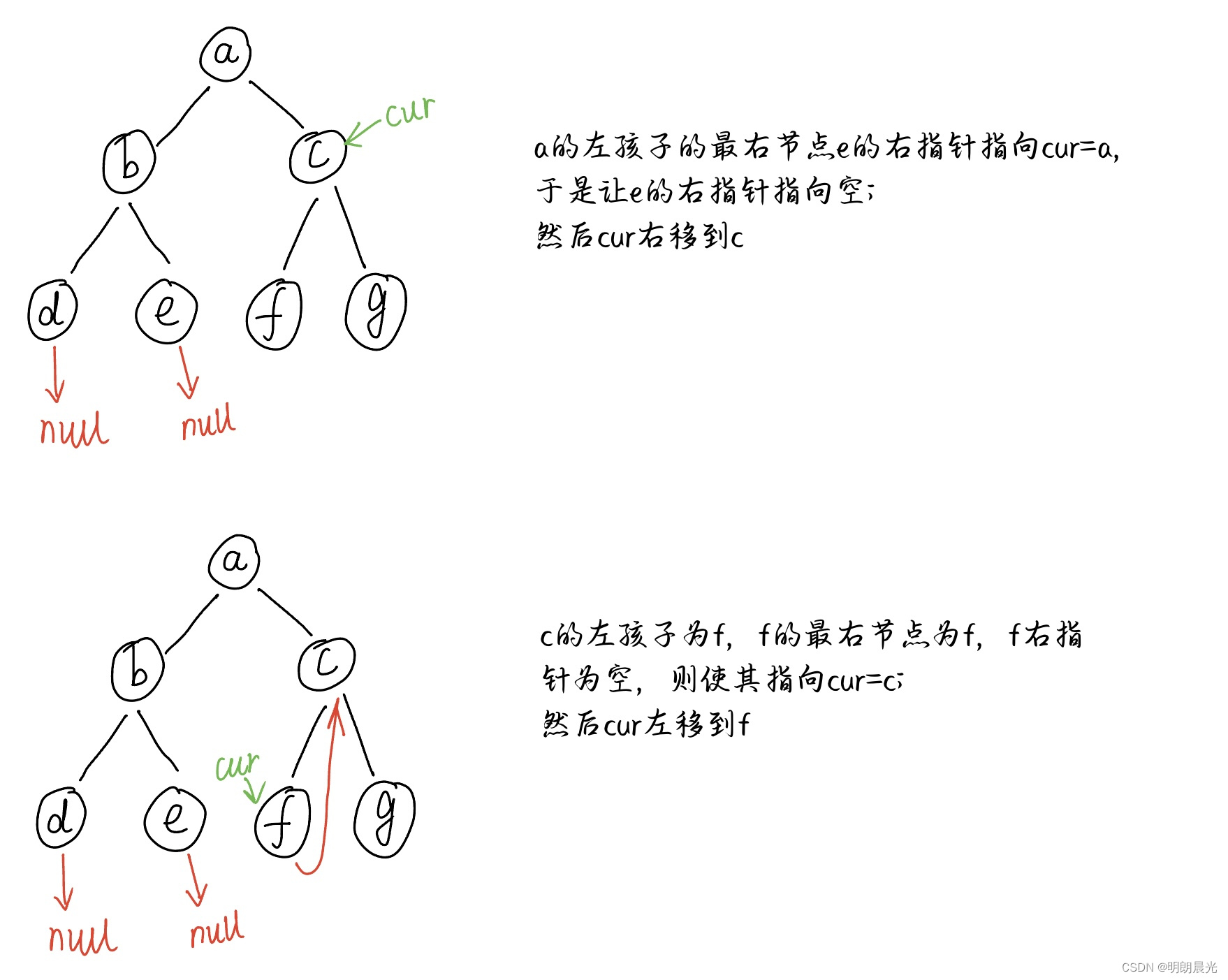
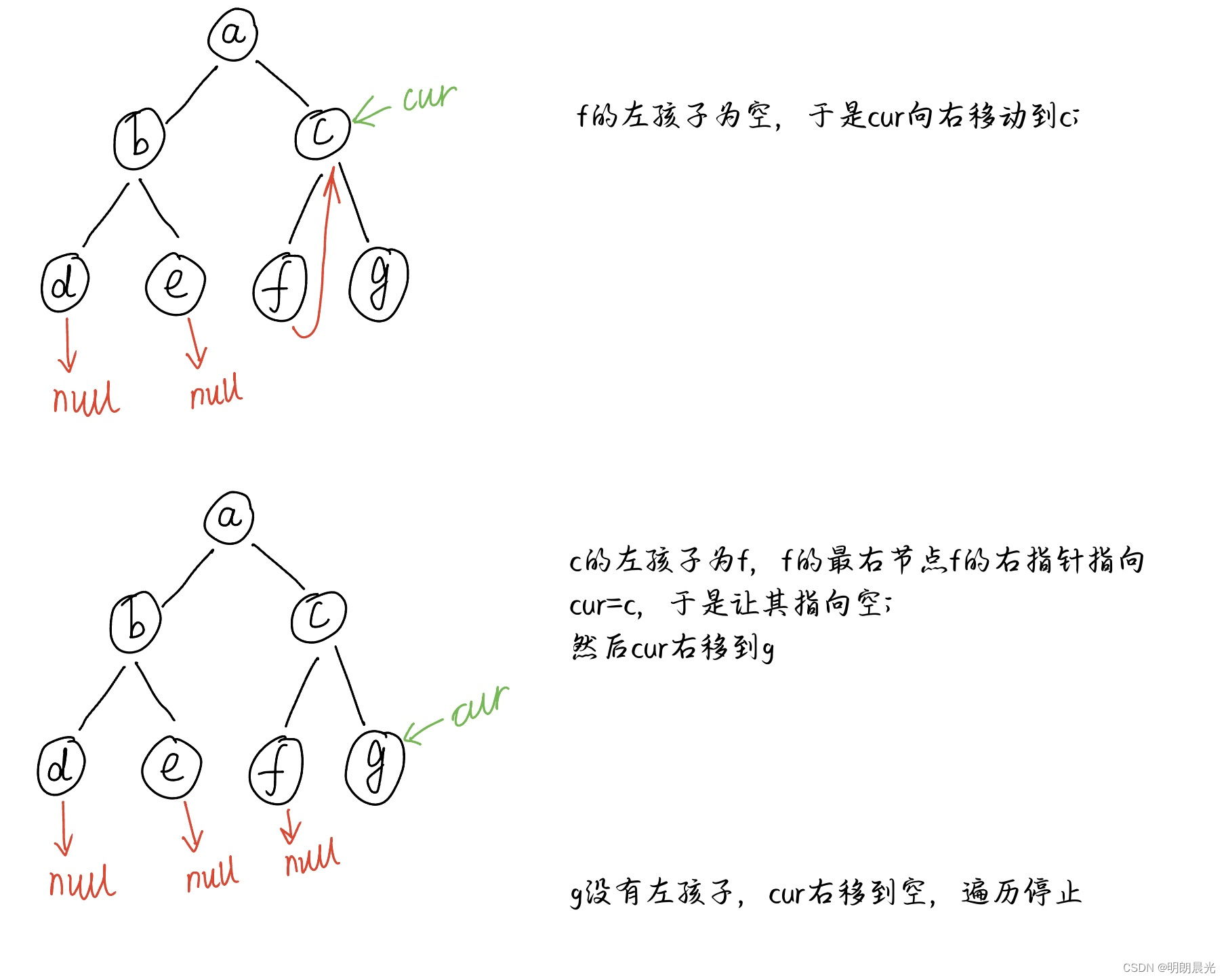
整个遍历过程访问各个节点的顺序:[a, b, d, b, e, a, c, f, c, g],这个顺序就叫做Morris序,该序的特点是有左树的节点会访问两次,并且是在遍历完该节点的左树后第二次来到这个节点。
该流程的实质是在用每个节点的左树上最右节点的右指针状态来标记到底是第一次还是第二次访问这个节点。 一开始 cur 指向头节点 a 时,左树上最右节点 e 的右指针指向空,所以是第一次来到 a;然后调整 e 的右指针指向 a,经过一些变换,最后 cur 又指向 a,而此时的 e 的右指针指向 a,所以是第二次来到 a。
4、通过Morris序加工出先序、中序和后序
Morris 序加工出先序:对于可以访问到两次的节点,在第一次访问到的时候就处理打印,第二次访问到的时候忽略;对于只访问一次的节点,就直接处理打印。
如上文的 Morris序:[a,b,d,b,e,a,c,f,c,g],处理得到的先序:[a,b,d,e,c,f,g]
Morris序加工出中序:对于访问到两次的节点,第一次访问到时忽略,第二次访问到时处理打印;对于只访问一次的节点,直接处理打印。
如上文的 Morris序:[a,b,d,b,e,a,c,f,c,g],处理得到的中序:[d,b,e,a,f,c,g]
Morris序加工出后序:处理时机放在能访问两次的节点的第二次访问上,当一个节点是第二次被访问时,逆序地打印它左树到右边界。
如上文的 Morris序:[a,b,d,b,e,a,c,f,c,g],处理时机只有标红的三个。
处理 b 的时候,逆序打印 b 的左树到右边界:d
处理 a 的时候,逆序打印 a 的左树到右边界:e,b
处理 c 的时候,逆序打印 c 的左树到右边界:f
Morris 序执行完后,单独逆序打印整棵树的右边界:g,c,a,使用链表反转实现
所以处理得到的后序:[d,e,b,f,g,c,a]
5、Morris遍历的实现
public class MorrisTraversal {
public static class Node {
public int value;
Node left;
Node right;
public Node(int data) {
this.value = data;
}
}
//树的递归遍历
public static void process(Node root) {
if (root == null) {
return;
}
// 1
process(root.left);
// 2
process(root.right);
// 3
}
//Morris遍历
public static void morris(Node head) {
if (head == null) {
return;
}
Node cur = head; //cur指针一开始在头结点
Node mostRight = null; //左树上的最右节点
while (cur != null) { //cur为空就停止
mostRight = cur.left; //指向左孩子
if (mostRight != null) { //左孩子不为空,即左树不为空
//找到最右节点
//因为有人为改的情况,所以当最右节点的右指针为空或者指向cur的时候停止
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
//此时的mostRight是cur左树上的最右节点
if (mostRight.right == null) {
mostRight.right = cur; //人为修改最右节点右指针的指向
cur = cur.left; //cur向左移动
continue;
} else { //mostRight的右指针指向cur
mostRight.right = null; //使mostRight的右指针指向空
}
}
cur = cur.right; //cur向右移动
}
}
//Morris遍历得到先序
//如果当前节点左树为空,则直接打印;如果左树不为空,在第一次访问的时候打印
public static void morrisPre(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) { //这是第一次访问到cur的时候
System.out.print(cur.value + " "); //所以直接打印
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
} else { //没有左树,则直接打印
System.out.print(cur.value + " ");
}
cur = cur.right;
}
System.out.println();
}
//Morris遍历得到中序
//如果当前节点左树为空,则直接打印;如果左树不为空,在第二次访问的时候打印
public static void morrisIn(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue; //第一次访问cur时,会continue不会往下执行
} else {
mostRight.right = null; //第二次访问到cur,会继续往下执行
}
}
//cur没有左树 和 cur第二次被访问到时都会执行该code
System.out.print(cur.value + " ");
cur = cur.right;
}
System.out.println();
}
// Morris遍历得到后序
// 每个节点访问其左树到右边界的节点2遍,但是所有节点遍历其左树右边界的规模也就是整棵树的规模,所以时间复杂度仍然是O(N)
public static void morrisPos(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
printEdge(cur.left); //第二次访问节点的时候逆序打印其左树到右边界
}
}
cur = cur.right;
}
//Morris完毕之后,逆序打印整棵树的右边界
printEdge(head);
System.out.println();
}
public static void printEdge(Node head) { //打印边界
Node tail = reverseEdge(head); //链表反转
Node cur = tail;
while (cur != null) {
System.out.print(cur.value + " ");
cur = cur.right;
}
reverseEdge(tail); //再反转回去
}
public static Node reverseEdge(Node from) { // 链表反转
Node pre = null;
Node next = null;
while (from != null) {
next = from.right;
from.right = pre;
pre = from;
from = next;
}
return pre;
}
// for test -- print tree
public static void printTree(Node head) {
System.out.println("Binary Tree:");
printInOrder(head, 0, "H", 17);
System.out.println();
}
public static void printInOrder(Node head, int height, String to, int len) {
if (head == null) {
return;
}
printInOrder(head.right, height + 1, "v", len);
String val = to + head.value + to;
int lenM = val.length();
int lenL = (len - lenM) / 2;
int lenR = len - lenM - lenL;
val = getSpace(lenL) + val + getSpace(lenR);
System.out.println(getSpace(height * len) + val);
printInOrder(head.left, height + 1, "^", len);
}
public static String getSpace(int num) {
String space = " ";
StringBuffer buf = new StringBuffer("");
for (int i = 0; i < num; i++) {
buf.append(space);
}
return buf.toString();
}
public static void main(String[] args) {
Node head = new Node(4);
head.left = new Node(2);
head.right = new Node(6);
head.left.left = new Node(1);
head.left.right = new Node(3);
head.right.left = new Node(5);
head.right.right = new Node(7);
printTree(head);
morrisIn(head);
morrisPre(head);
morrisPos(head);
printTree(head);
}
}
6、应用
很多题目都涉及到二叉树的遍历,利用Morris遍历可以改写得到最优解。
如,判断一棵树是否为搜索二叉树。
利用Morris遍历,就是在得到中序的过程中将打印行为替换为与前一个节点值比较即可。
public static boolean isBST(Node head) {
if (head == null) {
return true;
}
Node cur = head;
Node mostRight = null;
Integer pre = null; //中序遍历中上一个节点的值
boolean ans = true;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
}
if (pre != null && pre >= cur.value) {
ans = false;
}
pre = cur.value;
cur = cur.right;
}
//必须等Morris跑完之后才返回
//因为Morris遍历过程中有人为修改指针的情况,必须等整个遍历过程结束全部恢复之后再返回
return ans;
}