1. 前言

在前两篇博客中实现了遍历搜索所有的Tic-Tac-Toe的棋局的python程序实现。

Tic-Tac-Toe可能棋局搜索的实现（python）_笨牛慢耕的博客-CSDN博客Tic-Tac-Toe中文常译作井字棋，即在3 x 3的棋盘上，双方轮流落子，先将3枚棋子连成一线的一方获得胜利。Tic-Tac-Toe变化简单，可能的局面和棋局数都很有限（相比中国象棋、日本象棋、围棋等来说连九牛一毛都不到！具体有多少可能的局面以及可能的棋局数，本系列完成以后就可以给出答案了），因此常成为和搜寻的教学例子，同时也是的一道好题目。本系列考虑实现一个Tic-Tac-Toe AI，以由浅入深循序渐进的方式来逐步完成这个实现。https://blog.csdn.net/chenxy_bwave/article/details/128506352Tic-Tac-Toe可能棋局遍历的实现（python）_笨牛慢耕的博客-CSDN博客在上一篇博客中实现了搜索Tic-Tac-Toe游戏的某个棋局的python程序。接下来的问题是，在Tic-Tac-Toe游戏中总共有多少种可能的棋局呢？注意，棋局是指在两个player交替下棋直到终局的过程中所导致的棋盘状态变化的序列。所以，即便所包含的棋盘状态集合完全相同，但是如果棋盘状态出现的顺序不同的话，也是不同的棋局。本文在上一篇的基础上进一步实现搜索Tic-Tac-Toe游戏的所有可能棋局的实现。https://blog.csdn.net/chenxy_bwave/article/details/128513299

根据上一篇的实现（搜索Tic-Tac-Toe所有可能棋局），结果表明有255168种棋局，有5478种盘面状态。但是，这个结果对吗？

严格地来说是不对的。

因为以上实现没有考虑Tic-Tac-Toe游戏的棋盘的对称性。举个例子说，第一手下在四个角上的任意一个角上本质上都是一样的。考虑了对称性所导致的重复后，总的可能棋局数和盘面状态数会大幅度减小。

棋盘的对称性包含以下4种对称：

旋转对称
对角线对称
上下对称
左右对称

以上各种对称的示例如下图所示：

2. 如何去重？

如何将对称性考虑进去进行去重（repetition removal）处理以得到真正的不同棋局数和盘面状态数的结果呢？

本文给出的思路是：在棋局遍历过程计算某个节点的所有邻接节点时，追加去重判断，将满足以上所述各种对称性的状态视为相同的状态，只保留其中一个并剔除其余的。这样最后遍历的结果就代表本质上不相同的棋局。以下举两个例子。

例1：从初始棋盘状态，player1下第一手棋。

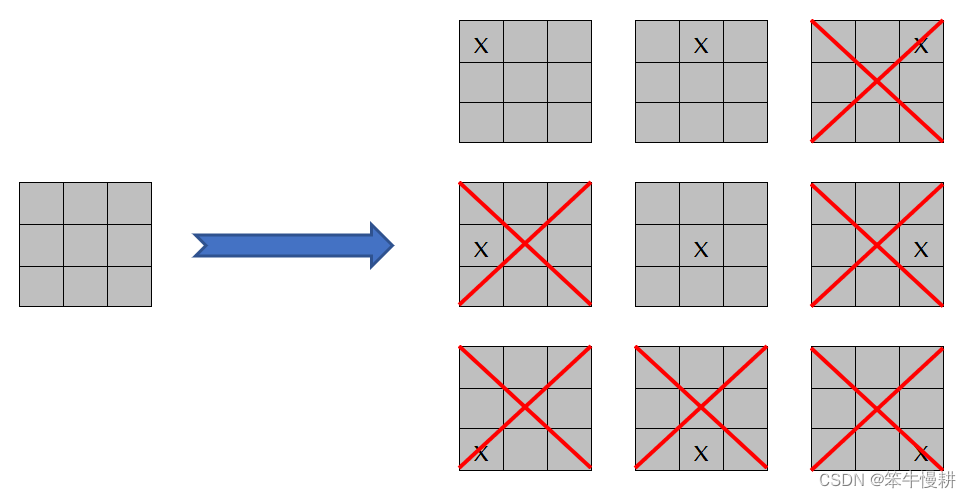
虽然，player应该可以在9个位置中的任意一处落子，但是考虑到对称性等价后，其实只剩下了3种可能。图中标为红色“X”标志的图即为由于对称等价而排除的局面。

例2：player1落子后，player2下棋的可能位置

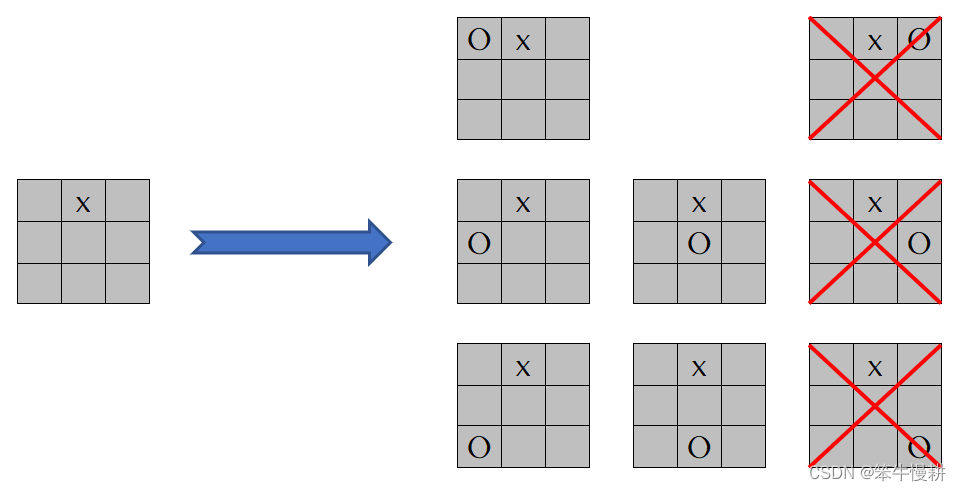
最后在基于棋局统计所有不同盘面状态时同样要进行去重处理，剔除重复的，最后得到的才是所有可能的不同棋盘状态。

3. 代码实现

3.1 对称等价判断

对称等价判断实现如下所示。这里采用的是最直接朴素的实现方式。应该有更高效的实现方案。

def is_rot_symmetry(s1,s2):
    rot90_symm = \
        s1[0] == s2[6] and s1[1] == s2[3] and s1[2] == s2[0] and \
        s1[3] == s2[7] and s1[4] == s2[4] and s1[5] == s2[1] and \
        s1[6] == s2[8] and s1[7] == s2[5] and s1[8] == s2[2]

    rot180_symm = \
        s1[0] == s2[8] and s1[1] == s2[7] and s1[2] == s2[6] and \
        s1[3] == s2[5] and s1[4] == s2[4] and s1[5] == s2[3] and \
        s1[6] == s2[2] and s1[7] == s2[1] and s1[8] == s2[0]

    rot270_symm = \
        s1[0] == s2[2] and s1[1] == s2[5] and s1[2] == s2[8] and \
        s1[3] == s2[1] and s1[4] == s2[4] and s1[5] == s2[7] and \
        s1[6] == s2[0] and s1[7] == s2[3] and s1[8] == s2[6]
        
    return rot90_symm or rot180_symm or rot270_symm
    
    
def is_diagonal_symmetry(s1,s2):
    symm1 = \
        s1[0] == s2[0] and s1[4] == s2[4] and s1[8] == s2[8] and \
        s1[1] == s2[3] and s1[3] == s2[1] and \
        s1[2] == s2[6] and s1[6] == s2[2] and \
        s1[5] == s2[7] and s1[7] == s2[5]

    symm2 = \
        s1[2] == s2[2] and s1[4] == s2[4] and s1[6] == s2[6] and \
        s1[1] == s2[5] and s1[5] == s2[1] and \
        s1[0] == s2[8] and s1[8] == s2[0] and \
        s1[3] == s2[7] and s1[7] == s2[3]
    
    return symm1 or symm2
    
def is_updown_symmetry(s1,s2):
    return \
        s1[0] == s2[6] and s1[1] == s2[7] and s1[2] == s2[8] and \
        s1[3] == s2[3] and s1[4] == s2[4] and s1[5] == s2[5] and \
        s1[6] == s2[0] and s1[7] == s2[1] and s1[8] == s2[2] 
    
def is_leftright_symmetry(s1,s2):
    return \
        s1[0] == s2[2] and s1[3] == s2[5] and s1[6] == s2[8] and \
        s1[1] == s2[1] and s1[4] == s2[4] and s1[7] == s2[7] and \
        s1[2] == s2[0] and s1[5] == s2[3] and s1[8] == s2[6] 
    
def is_symmetry(s1,s2):
    return is_rot_symmetry(s1,s2) or       \
            is_diagonal_symmetry(s1,s2) or \
            is_updown_symmetry(s1,s2) or   \
            is_leftright_symmetry(s1,s2)

3.2 find_neighbor()改造

在原来的find_neighbor()的基础上追加对称等价判断以去除重复盘面状态，得到代码如下：

def find_neighbor(s):
    neighbor_list = []
    # decides whose turn
    if s.count(1) == s.count(2):
        turn = 1
    elif s.count(1) == s.count(2) + 1:
        turn = 2
    else:
        print('Invalid input state: ', s)
        return None
    
    for k in range(len(s)):
        if s[k] == 0:
            s_next = list(s)
            s_next[k] = turn
            neighbor_list.append(tuple(s_next))

        
    neighbor_list2 = []
    
    for k in range(0,len(neighbor_list)):
        is_unique = True
        for s in neighbor_list2:
            if is_symmetry(neighbor_list[k], s):
                is_unique = False
                break
        if is_unique:
            neighbor_list2.append(neighbor_list[k])            
            
    return neighbor_list2

3.3 主程序及运行结果

其它函数没有修改（请参考上一篇）。

主程序中最后统计所有可能的盘面状态时同样追加基于对称判断的去重处理。代码如下：

if __name__ == '__main__':

    # Initialization
    s0     = tuple([0] * 9)
    path   = [s0]
    tStart = time.time()
    dfs(path)
    tStop  = time.time()
    
    state_set = set() # set() remove the repeated items automatically
    for k in range(len(path_list)):
        path = path_list[k]
        
        for s in path:
            state_set.add(s)
                 
    # Counting the different board status, with symmetrically repeated ones
    # states = state_set
    states = []
    for s1 in state_set:
        is_unique = True
        for s2 in states:
            if is_symmetry(s1, s2):
                is_unique = False
                break
        if is_unique:
            states.append(s1)                        
    
    print('Totally there are {0} games'.format(len(path_list)))
    print('Totally there are {0} board states'.format(len(states)))
    print('Time cost:  {0:6.2f} seconds'.format(tStop-tStart))

运行结果如下：