在此前一篇文章 《算法效果评估：均方根误差（RMSE）/ 标准误差》中，我们介绍了方差/标准差的计算方法，也点出了它们是用来“度量数据离散程度”的一种数学方法，但是对于它们的意义并没有给出更具体和形象的解释。本文，我们把这块内容补上。

一言以蔽之，方差/标准差是用来度量数据离散程度的，或者应该再精确一点说应该是：方差/标准差是用来度量一组数据距离某个中心位置（均值或数学期望）的离散程度的。反之，我们也可以在一些工具中通过设定方差/标准差的大小来生成离散程度不同的数据集，本文，我们就用这种方法来帮助我们理解方差/标准差的意义。

案例：箭靶

先不考虑任何数学知识，我们来看一个再形象不过的示例：枪靶

上图中蓝色和黄色的点位是两个人的射击成绩，我们把每一个点位的正负值考虑进去，蓝色和黄色的点到中心点的平均距离都为0，因为x,y轴有正负值，多点叠加会相互抵消，虽然实际情况未必会如此精准，但我们完全可以通过造数据的方式来生成一张到靶心的平均距离为0的图。注意：我们这里强调两种颜色的点到中心点的平均距离都为0实际上是在强调：两套样本的均值都是0（确切地说是（x=0,y=0）），也就是说：这些点是均匀地围绕靶心分布的，它反映的是“射击者在瞄准时总是尽量指向靶心”这一趋势，这也符合人们的直观感受。实际上，这里的靶心就是我们常说的“数学期望”，在保持相同数学期望（同一均值）的情况下去对比离散程度（方差）会更严谨也更直观一些。

现在，我们来看一下谁的射击成绩更好？答案是非常确定的：蓝色的成绩更好，不用计算具体的环数，只从视觉上就可以看到：蓝色的点位相比于黄色更加集中在圆心位置，它的离散程度远远小于黄色点位，那么箭靶上的这种点位的离散程度怎么用数据来说明（表征）呢？其实这就是方差/标准差。

案例：身高

由于箭靶的点位是一个由横纵坐标组成的二维数据，比较我们计算方差时使用的一维样本数据还是不太方便直接理解。我们再选一个一维数组来帮助我们理解方差/标准差。

考虑人类的身高数据，这是一个典型的符合正态分布的数据，我们假设正常人的身高集中在以170cm为中心，150cm- 190cm的区间内，则大多数人的身高会集中于170cm上下的区间内，越向两侧延伸（更高或更矮），人数越少。为此，我们可以利用numpy生成两个符合这一正态分布的数据集，但是设置不同的方差，然后观察一下它们的“离散”程度:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline

def gen_heights(sample_scale, sample_size):
    # 以170cm为正态分布的中心点，给定的样本数量和标准差，生成一维数组
    # 注：scale参数是指定的标准差，该值越大，样本越发散，越小，样本越集中
    heights = np.random.normal(loc=170, scale=sample_scale, size=sample_size)
    # print(f"heights variance = {heights.var()}")
    print(f"scale = {sample_scale}, heights standard deviation = {heights.std()}")
    # print(heights)
    # print(heights.shape)

    # 将其转置为二维表结构:n行1列，就是行转列操作，-1在reshape中的含义是：不手动计算这个维度的数量
    # 由numpy自动去计算。这里只需要控制列数=1即可
    heights = heights.reshape(-1, 1)
    # print(heights)
    # print(heights.shape)

    zeros = np.zeros(sample_size)

    # axis=1, 是在水平方向上插入zeros数组，所以效果上就是“扩列”
    # 插入位置是0（在第1个位置上插入）,故最终的形式为[[0,a], [0,b], ...]
    heights = np.insert(heights, 0, zeros, axis=1)
    # print(heights)

    return pd.DataFrame(heights, columns=['0','height'])
    
df1 = gen_heights(2, 20)
df2 = gen_heights(6, 20)

# 设置图形属性及布局
plt.style.use('ggplot')
fig1 = plt.figure('身高分布')
axes1 = fig1.subplots(nrows=1, ncols=2)
ax1, ax2 = axes1.ravel()

df1.plot(kind="scatter", color="red", ax=ax1, x="height", y="0", figsize=(12,5), xlim=(150, 190))
df2.plot(kind="scatter", color="green", ax=ax2, x="height", y="0", figsize=(12,5), xlim=(150, 190))

程序输出：

scale = 2, heights standard deviation = 1.8318180277200293
scale = 6, heights standard deviation = 5.444879647398637

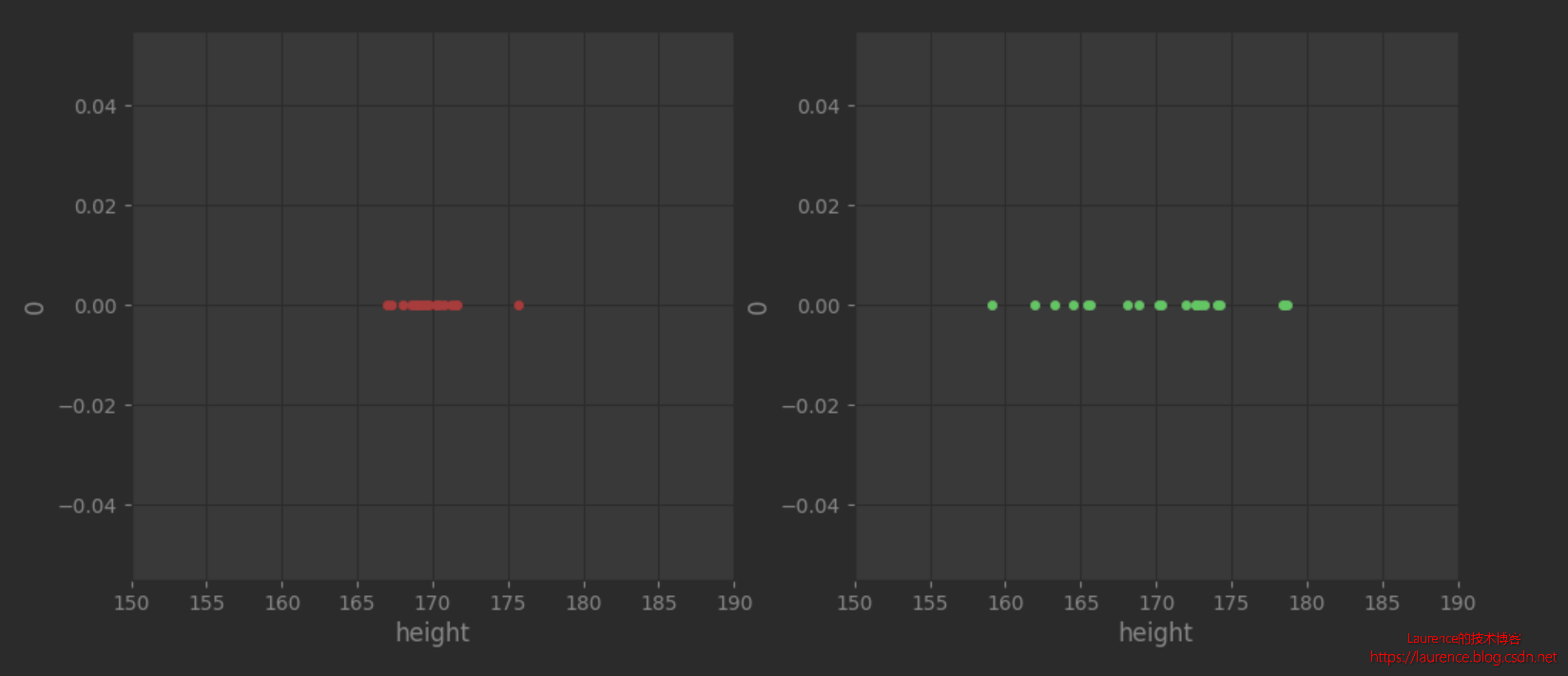
我们先看图片，两图都是随机生成的以170为中心符合正态分布的20个身高数据，从图上发现：图2明显比图1发散（两张图的横纵轴范围一样，无缩放）。同样是20个数据，是什么因素导致两者的离散程度有如此明显的差异呢？其实关键就是他们的“方差”不同。

在程序中，我们特别打印了生成数据的方差值：

• 第一组数据设定的scale=2，实际生成数据的标准差是1.8
• 第二组数据设定的scale=6，实际生成数据的标准差是5.4

将标准差和其对应的图形联系在一起，我们就可以很直观地感受到：方差所描述的正是数据的离散程度。

最后，补充解释一下为什么实际生成数据的标准差和通过scale设定的期望标准差有出入，原因是由于数据是随机生成的，很难保证精确的方差值，特别是在数据样本比较少的情况下，如果我们把样本数量从20提高到2000，我们就会发现，实际生成数据的标准差就会稳定在2左右，很少会出现大的波动。

案例：身高+体重

由于单纯的身高数据是一维的数组，他们的稀疏只能在数轴上体现，还是不够直观。我们现在把人的体重数据补充进来，以身高为横轴，体重为纵轴，一个点代表一个人（他的身高和体重），然后再次利用numpy生成这样的二维数组，让身高和体重都服从正态分布，其中身高数据与上例相同，体重数据以60KG为中心点，然后设置不同的标准差，观察它们的离散程度：

def gen_heights_weights(sample_scale, sample_size):
    # 分别生成height和weight的正态分布数据
    heights_weights = np.random.normal(loc=(60,170), scale=sample_scale, size=sample_size)
    print(f"scale = {sample_scale}, heights standard deviation = {heights_weights.std(axis=0)}")
    return pd.DataFrame(heights_weights, columns=['weight','height'])

df3 = gen_heights_weights((2,2),(100,2))
df4 = gen_heights_weights((6,6),(100,2))

# 设置图形属性及布局
plt.style.use('ggplot')
fig2 = plt.figure('身高-体重分布')
axes2 = fig2.subplots(nrows=1, ncols=2)
ax3, ax4 = axes2.ravel()

df3.plot(kind="scatter", color="red", ax=ax3, x="height", y="weight", figsize=(12,5), xlim=(150, 190), ylim=(40, 80))
df4.plot(kind="scatter", color="green", ax=ax4, x="height", y="weight", figsize=(12,5), xlim=(150, 190), ylim=(40, 80))

程序输出：

scale = (2, 2), heights standard deviation = [2.00995395 1.94059452]
scale = (6, 6), heights standard deviation = [6.06434877 5.58389361]

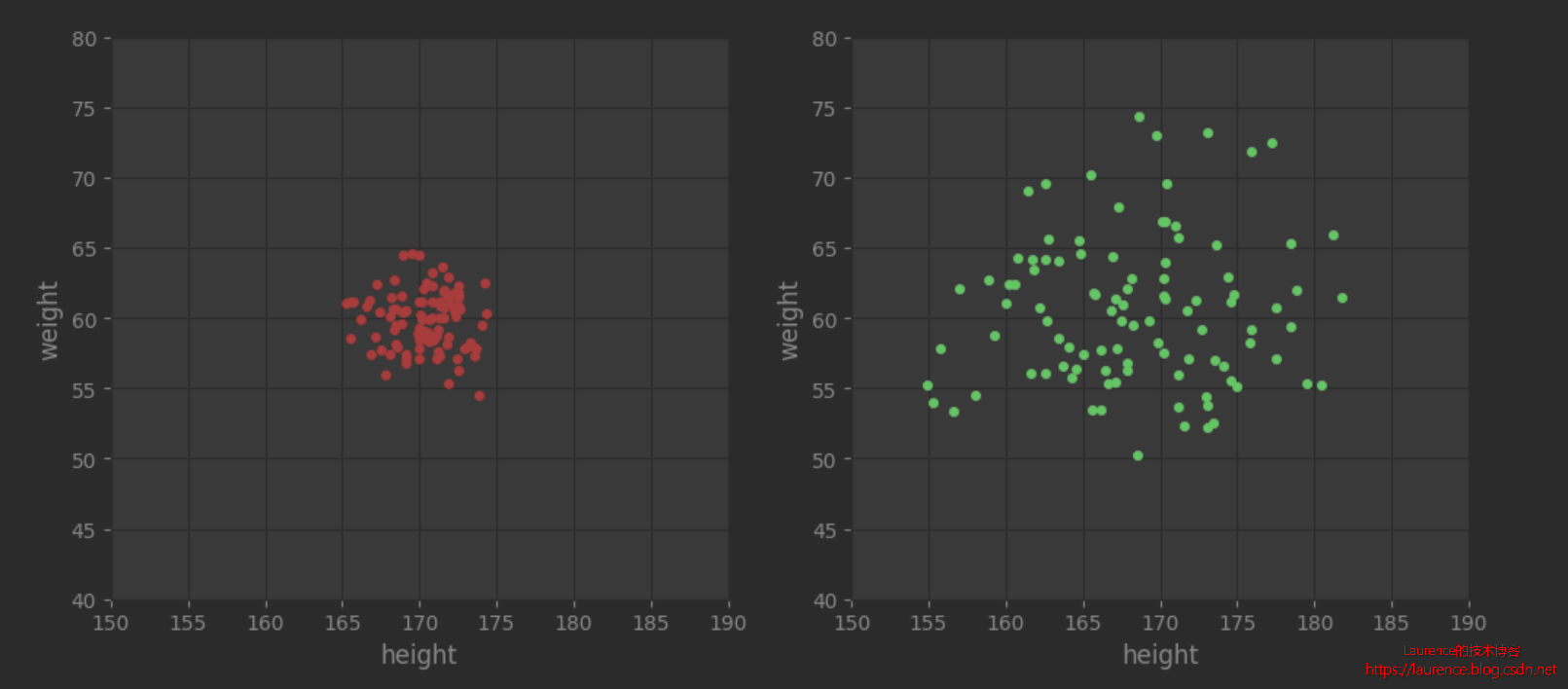
同样是先观察一下图片，升级为2维数据后，收敛和发散的趋势就更加鲜明了，如果这是枪靶数据，发散和收敛的含义非常清晰。但是由于这两组数据是我们人工制造的，所以数据本身并没有说明价值。只能说左侧的人群受到相同的先天和后天因素的影响，身高和体重较为集中在标准范围内；而右侧的人群由于先天和后天因素都有很大差异（可以假设是从不同地区，不同职业，不同生活习惯等维度选出的），所以身高和体重的差异非常大。

---

参考

https://www.cnblogs.com/traditional/p/12629050.html

https://www.sharpsightlabs.com/blog/numpy-random-normal/