目录
学习目标
1.分布式事务理论基础
1.1.本地事务
1.2.分布式事务
分布式事务产生的原因?
哪些场景会产生分布式事务?
单体系统会产生分布式事务问题吗?
只有一个库,会产生分布式事务问题吗?
分布式事务举例
分布式服务的事务问题
2. 解决分布式事务的理论基础
2.1 CAP定理
1. 一致性
2. 可用性
3. 分区容错
矛盾:
结论:
CAP权衡
思考:Elasticsearch集群是CP还是AP?
2.2 BASE理论
2.3 ACID和BASE的区别与联系?
2.4 解决分布式事务的思路
学习目标
- 分析分布式事务产生的原因:跨服务、跨数据源的业务
- 思考解决分布式事务的基本思路
- 了解Seata框架,学习Seata原理
- 利用Seata解决分布式事务问题
1.分布式事务理论基础
1.1.本地事务
本地事务,也就是传统的单机事务,在传统的数据库事务中,必须要满足ACID四个原则:
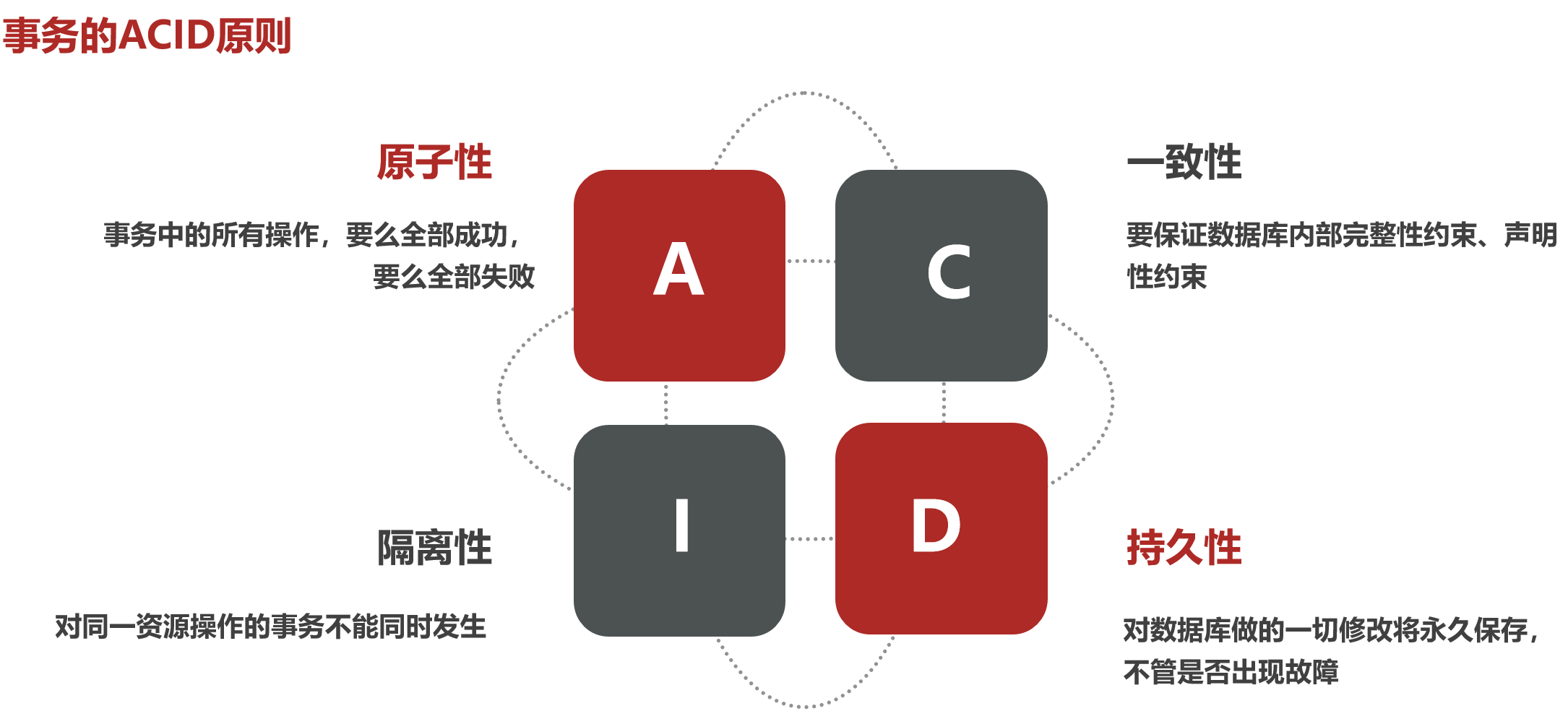
但是现在我们要研究的是微服务,而微服务的业务往往比较复杂,可能一个业务就会跨越多个服务,而每个服务又会有自己独立的数据库,也就是独立的事务,这个时候你再靠数据库本身的特性,就很难保证整个业务的ACID了。
1.2.分布式事务
分布式事务,就是指不是在单个服务或单个数据库架构下产生的事务。
- 分布式事务是指涉及多个独立系统或服务的事务处理,在分布式系统中,不同的服务或应用程序可能被部署在不同的服务器上,这些服务需要协同工作来完成一个事务,事务的每个操作步骤都位于不同的节点上,需要保证事务的ACID与特性。
- 在传统的单机环境下,事务处理通常由单一的事务管理器(Transaction Manager)来管理,保证事务的原子性、一致性、隔离性和持久性(ACID),但在分布式系统中,由于存在网络延迟、节点故障等问题,事务处理变得更加困难。
分布式事务产生的原因?
- 每个微服务的本地事务,也可以称为分支事务,每一个分支事务就是传统的单体事务,多个有关联的分支事务一起就组成了全局事务,但全局事务跨多个服务、跨多个数据库,因此全局事务,即分布式事务并未遵循ACID的原则,归其原因就是参与事务的多个子业务在不同的微服务中,跨越了不同的数据库,虽然每个单独的业务都能在本地遵循ACID,但是它们互相之间没有感知(各个分分支事务之间互相是感知不到的),不知道有人失败了,无法保证最终结果的统一,也就无法遵循ACID的事务特性了,所以,我们必须保证整个全局事务同时成功或失败。
哪些场景会产生分布式事务?
1. 跨数据源或跨数据库实例的分布式事务
比如有以下两个场景:
- 单体系统下,同一个系统使用了多个数据库源连接不同的数据库
- 分布式、微服务系统,各系统服务使用不同的数据库
2. 跨服务,即跨JVM进程的分布式事务
- 分布式、微服务系统,各系统服务使用不同的数据库或者是同一个数据库,都会产生分布式事务,因为它们使用的是不同的数据库连接和事务管理器
单体系统会产生分布式事务问题吗?
- 会,如果一个单体系统使用了多个数据源连接不同的数据库,也会产生分布式事务问题。
只有一个库,会产生分布式事务问题吗?
- 分布式、微服务系统,各系统服务使用不同的数据库,或者是同一个数据库,都会产生分布式事务,因为它们使用的是不同的数据库连接和事务管理器。
分布式事务举例
- 在数据库水平拆分、服务垂直拆分之后,一个业务操作通常要跨多个数据库、服务才能完成。
例如电商行业中比较常见的下单付款业务的整体流程,包括下面几个行为: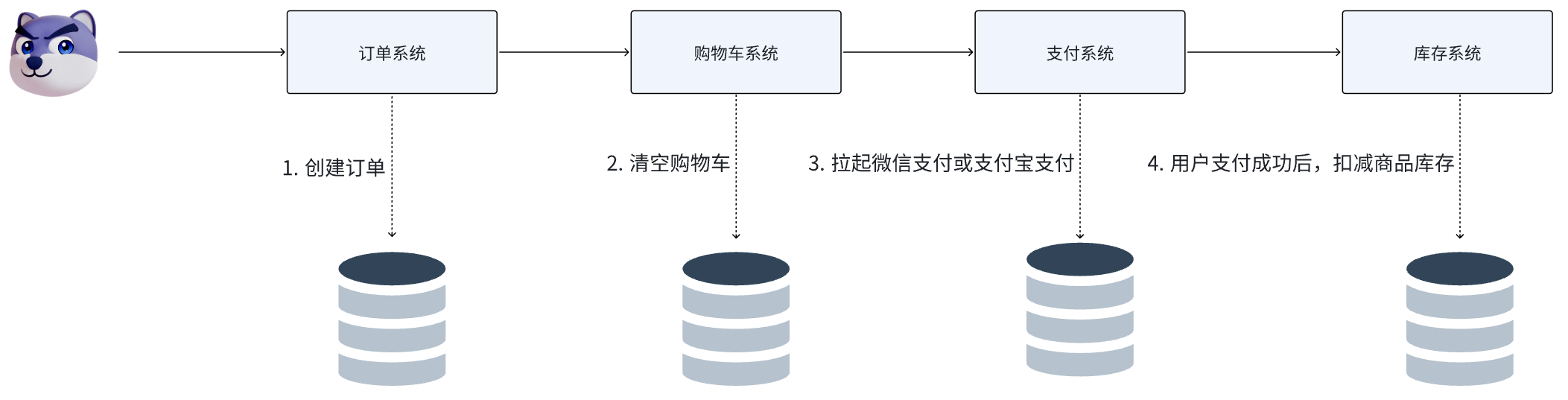
完成上面的操作需要访问四个不同的微服务和四个不同的数据库,订单的创建(创建订单并写入数据库)、购物车的清空、账户的扣款(用户账户余额的扣减)、商品库存的扣减在每一个服务和数据库内是一个本地事务,可以保证ACID原则,但我们最终希望的肯定是我这个下单业务一旦执行,每一个都要成功,但是当我们把这几件事情看做一个"业务",要满足"业务"的原子性,要么所有操作全部成功,要么全部失败,不允许出现部分成功部分失败的现象,这就是分布式系统下的事务了,但此时ACID难以满足,这就是分布式事务要解决的问题。
- 父工程,负责管理项目依赖。
分布式服务的事务问题
- 在分布式系统下,一个业务跨越多个服务或数据源,每个服务都是一个分支事务,要保证所有分支事务最终状态一致,这样的事务就是分布式事务。
2. 解决分布式事务的理论基础
- 解决分布式事务问题,需要一些分布式系统的基础知识作为理论指导。
- CAP定理和BASE理论这两个概念就是指导我们解决分布式事务的具体方向。
2.1 CAP定理
1998年,加州大学的计算机科学家 Eric Brewer 提出,分布式系统有三个指标:
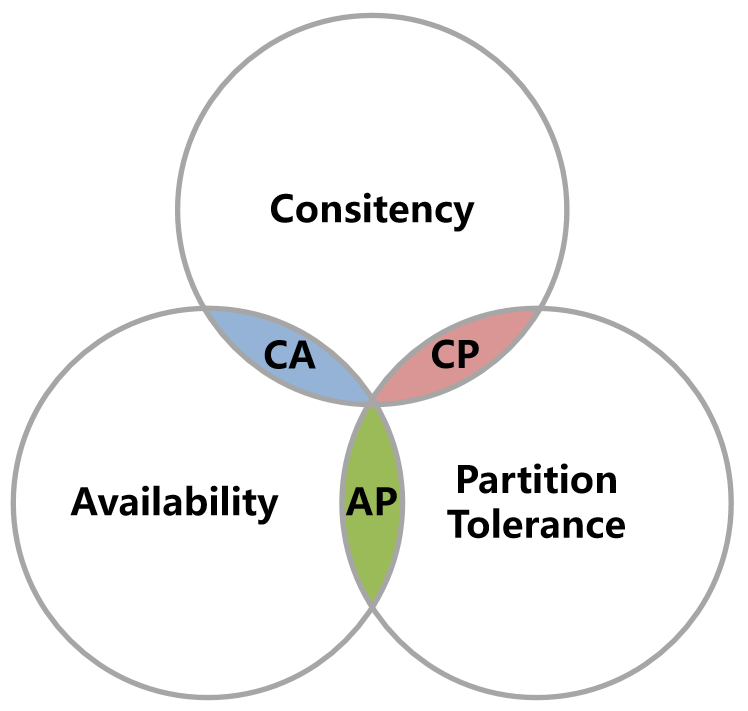
-
Consistency(一致性):同一个数据在同一时刻是相同的 => 强一致性
-
Availability(可用性)
-
Partition tolerance (分区容错性)
它们的第一个字母分别是C、A、P,Eric Brewer认为任何分布式系统架构方案都不可能同时满足这3个目标,这个结论就叫做 CAP 定理,CAP定理又称CAP原则。
1. 一致性
Consistency(一致性):用户在访问分布式系统中的任意节点时,得到的数据必须是一致的。
- 比如现在包含两个节点,其中的初始数据是一致的:
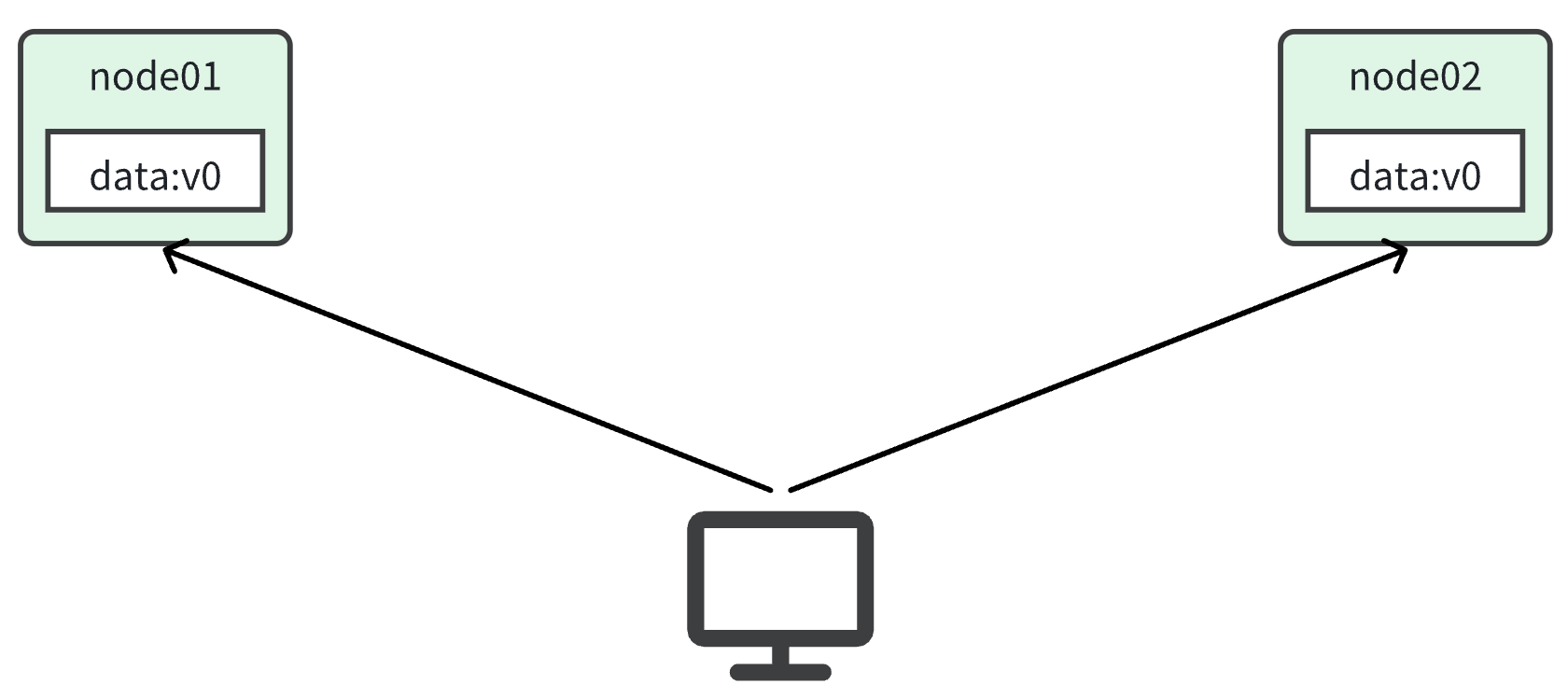
- 当我们修改其中一个节点的数据时,两者的数据产生了差异:

- 要想保住一致性,就必须实现node01 到 node02的数据 同步,所以,作为一个分布式系统,在做数据备份的时候,一定要及时的去完成数据同步,这样才能满足一致性:

2. 可用性
Availability (可用性):用户在访问集群中的任意健康节点或非故障节点时,必须能得到响应,而不是超时或拒绝或阻塞。
- 用户访问分布式系统时,读或写操作总能成功。
- 只能读不能写,或者只能写不能读,或者两者都不能执行,就说明系统弱可用或不可用。
3. 分区容错
Partition(分区):就是当分布式系统节点之间因为出现网络故障或其它原因导致分布式系统中的部分节点之间无法通信的情况,导致分布式系统中的部分节点与其它节点失去连接,形成独立分区。
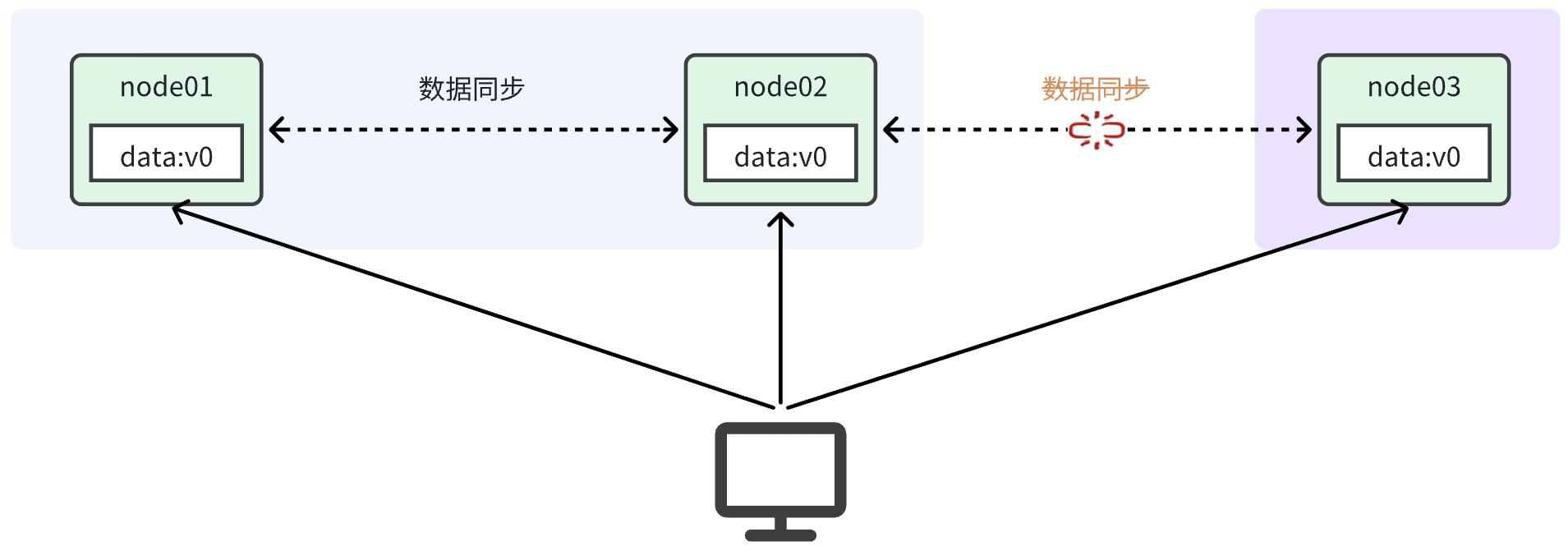
如上图,node01和node02之间网关畅通,但是与node03之间网络断开,于是node03成为一个独立的网络分区;node01和node02在一个网络分区。
Tolerance(容错):在集群出现分区时,整个系统仍能持续对外正常提供服务。
矛盾:
当出现网络分区时,如图:
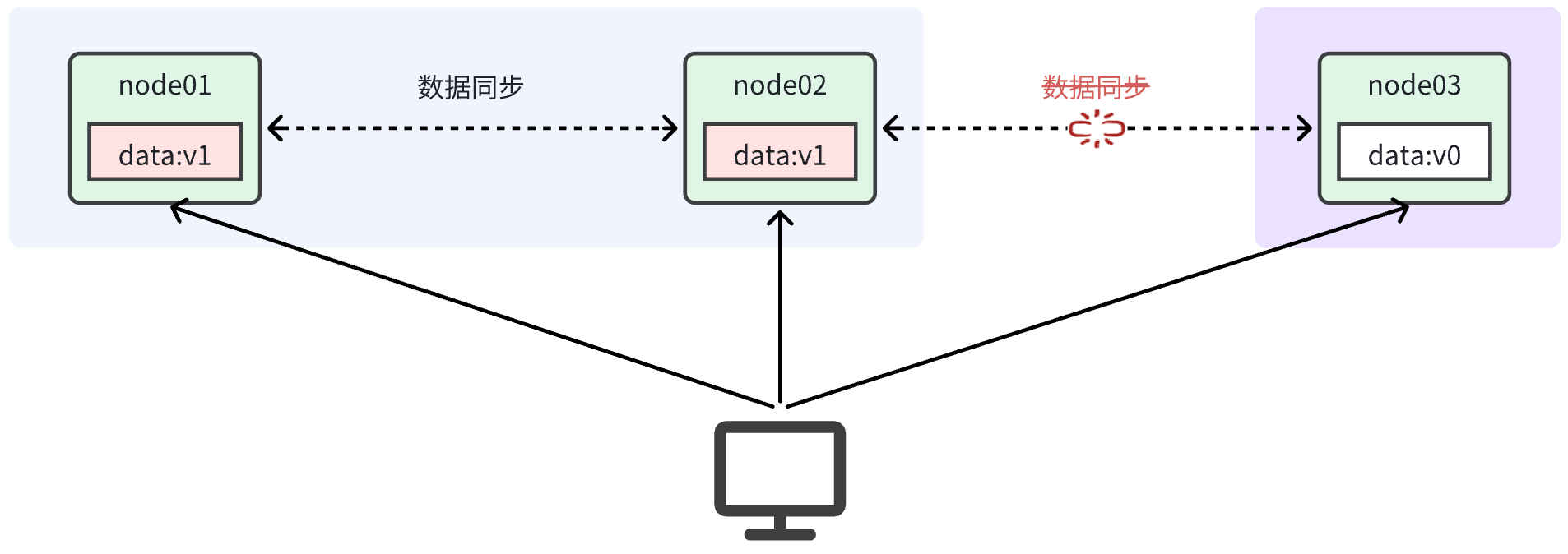
由于网络故障,当我们把数据写入node01时,可以与node02完成数据同步,但是无法同步给node03。现在有两种选择:
-
允许用户任意读写,保证可用性,那就不能等待网络恢复,但由于node03无法完成数据同步,就会出现数据不一致的情况,满足AP。
-
不允许用户任意读写,用户请求到node03节点时直接阻塞该用户请求,直到网络恢复,分区消失,完成数据同步后,该节点才对外提供服务,此时再唤醒被阻塞的用户线程,再让用户正常去访问,这样就确保了数据的一致性,但牺牲了可用性,因此node03节点是一个健康的节点,而你用户打进来却被该节点阻塞了,此时不就是牺牲了可用性,满足CP。
结论:
- 当网络出现分区时,一致性(C)和可用性(A)系统无法同时满足,你要保证数据的一致性那你就要牺牲系统的可用性,你要保证系统的可用性,那一致性就无法满足,而在分布式系统中,网络不能100%保证畅通(因为只要你是一个分布式系统,你的节点之间一定是通过网络连接的,而只要你是通过网络连接的,你就没有办法保证网络100%是健康的),也就是说网络分区的情况一定会存在,因此Partition Tolerance 它是不可避免的,而我们的整个系统又必须要持续运行,对外提供服务,所以分区容错性(P)是硬性指标,所有分布式系统都要满足,而在设计分布式系统时要取舍的就是一致性(C)和可用性(A)了, 所以三者只能是CP(强一致性)或者AP(高可用性)。
CAP权衡
- 舍弃P在分布式系统中几乎是不存在的,首先在分布式环境下,网络分区是一个自然的事实,因为分区是必然的,所以如果舍弃P,意味着就要舍弃分布式系统,那也就没有必要再讨论CAP理论了,所以,对于一个分布式系统来说,P是一个基本要求,CAP三者中,只能再CA两者之间做权衡,并且要想进办法提升P。
- 要想提升系统的分区容错性,需要通过提升基础设施的稳定性来保证。
思考:Elasticsearch集群是CP还是AP?
- 当ES集群出现分区时,故障节点会被集群剔除,故障节上面的数据分片会重新分配到其它健康的节点上去,保证了数据一致性,因此Elasticsearch集群属于CP,满足高一致性、低可用性的这样一个集群。
2.2 BASE理论
既然分布式系统要遵循CAP定理,那么问题来了,我到底是牺牲一致性还是可用性呢?如果牺牲了可用性,出现数据不一致该怎么处理?
因此就出现了BASE理论,BASE理论是对CAP的一种解决思路,包含三个思想:
- Basically Available(基本可用):分布式系统出现故障时,允许损失部分可用性,即或来保证核心可用。
- Soft State(软状态):在一定时间内,允许系统出现中间状态,比如临时的不一致状态,而该中间状态不会影响系统的整体可用性 => 最终达到数据的一致性(最终一致性)。
- Eventually Consistent(最终一致性):虽然无法保证强一致性,但是在软状态结束后,最终达到数据的一致性。
简单来说,BASE理论就是一种取舍的方案,不再追求完美,而是最终达成目标,BASE理论是对CAP中一致性和可用性的一个权衡,核心思想是即使无法做到强一致性(Strong Consistency,CAP的一致性就是强一致性),但每个应用都可以根据自身的业务特点,采用适当的方式来使得系统达到最终一致性。
2.3 ACID和BASE的区别与联系?
- ACID是传统数据库常用的设计理念,追求强一致性模式,而BASE支持的是大型分布式系统,提出牺牲强一致性获得高可用性。
- ACID和BASE代表了两种截然相反的设计哲学,在分布式系统设计的场景中,系统组件对一致性要求是不同的,因此ACID和BASE又会结合使用。
2.4 解决分布式事务的思路
分布式事务最大的问题就是各个子事务的一致性问题,可以借鉴CAP定理和BASE理论,因此解决分布式事务有两种解决思路或有两个方向:
- AP模式 - 最终一致思想:即满足可用性,牺牲一定的一致性,各个子事务分别执行和提交(肯定有的成功有的失败),无需锁定数据,允许出现结果的不一致(处于软状态),如果有不一致的情况,再想办法采用弥补措施恢复数据即可,实现最终一致,例如AT模式就是如此。
- CP模式 - 强一致思想:各个子事务执行完成之后不要提交,而是互相等待,等待彼此结果,然后同时或统一提交或回滚,达成强一致,在这个过程中锁定资源,不允许其他人访问,数据处于不可用状态,但能保证一致性,但事务等待过程中,处于弱可用状态(因为在在这个过程中锁定资源,不允许其他人访问),例如XA模式。
但不管是哪一种模式,都需要在子系统事务之间互相通讯、协调事务状态,也就是需要一个事务协调者(TC),来帮助分布式事务中的各个子事务进行一个通信或感知对方彼此的状态:
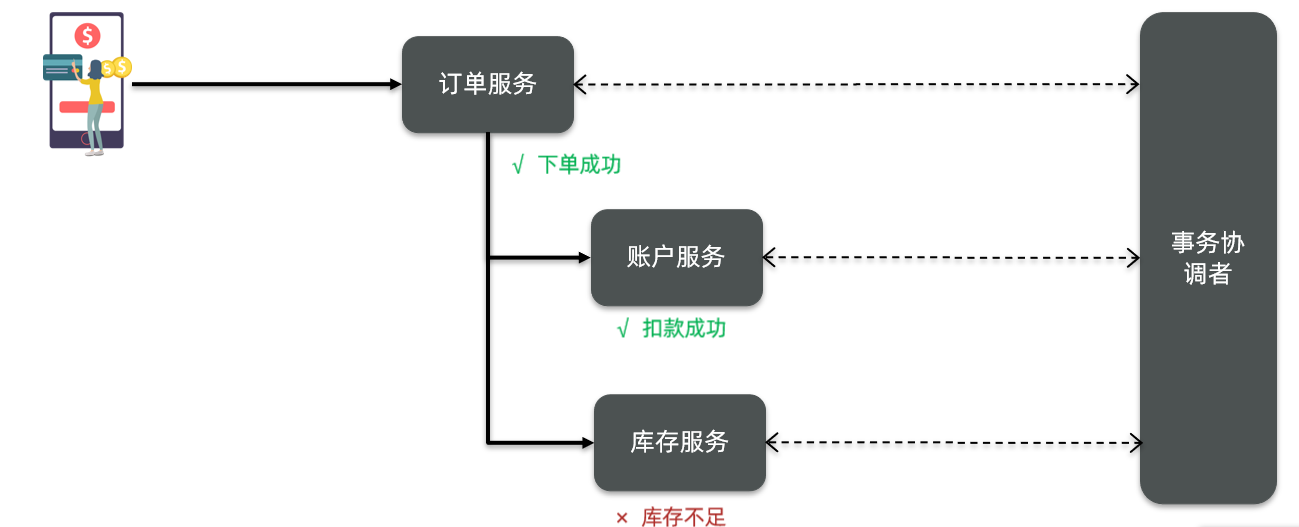
这里的子系统事务,称为分支事务,有关联的各个分支事务在一起称为全局事务。
- 全局事务:即整个分布式事务
- 分支事务:分布式事务中包含的每个子系统的事务