题目：142. 环形链表 II
我们知道，判断一个链表是否为环是这样的：

public boolean hasCycle(ListNode head) {
        ListNode slow = head,quickly = head;
        while(quickly != null && quickly.next != null){
            slow = slow.next;
            quickly = quickly.next.next;
            if(slow == quickly){
                return true;
            }
        }
        return false;
    }

这是我们常用的用快慢指针寻找是否有环的方法。
我们先深入分析一下其中可以挖掘到的信息：
设一开始slow的速度为v₁，quickly的速度为v₂，其中v₂= 2v₁。那么在经历相同时间内运行过的距离，x₂=2x₁，所以我们可以理解为，在t时刻时相遇，那么quickly走过的距离一定是slow走过的距离的二倍。

由此我们可以引申为，是不是不论什么时候，在v₂= 2v₁时，总有x₂=2x₁？答案很明显，是的，所以这道题目876. 链表的中间结点的解不就出来了？

我们回到这个题目上，假设相遇时相遇点距离环起点的距离为m，相遇点距离链表头结点的距离为k，所以有x₁=k，x₂=2k。那么这道题目的具体流程就可以是：

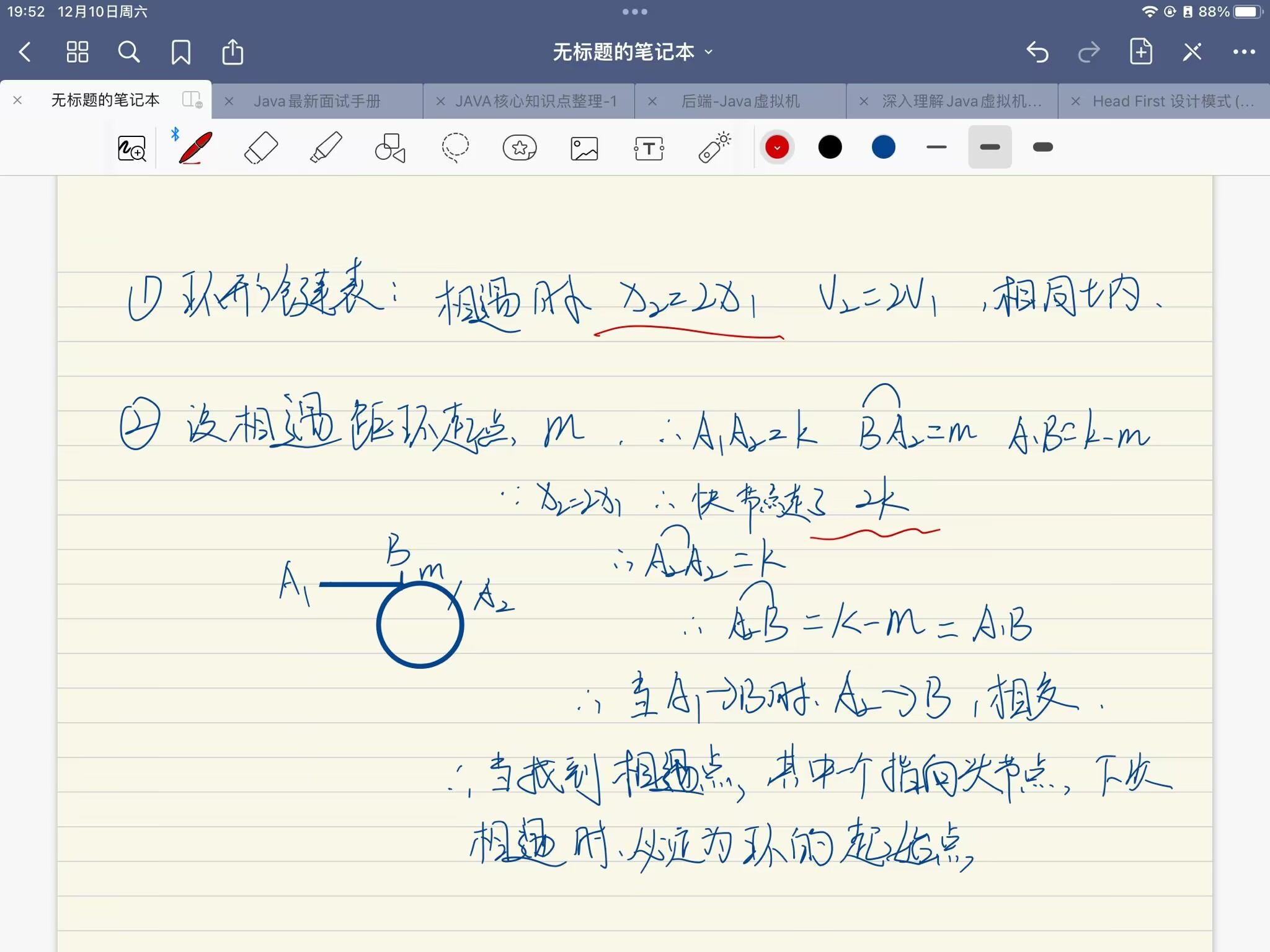
所以这道题目的解就是：

 public ListNode detectCycle(ListNode head) {
        ListNode quickly = head;
        ListNode slow = head;
        while(quickly != null && quickly.next != null){
            slow = slow.next;
            quickly = quickly.next.next;
            if(slow == quickly) break;
        }
		
        //排除链表不是环的情况
        if(quickly == null || quickly.next == null) return null;

        slow = head;
        while(slow != quickly){
            //同时开始走相同的距离，相遇就是环起点
            slow = slow.next;
            quickly = quickly.next;
        }

        return slow;
    }