《异常检测——从经典算法到深度学习》
- 0 概论
- 1 基于隔离森林的异常检测算法
- 2 基于LOF的异常检测算法
- 3 基于One-Class SVM的异常检测算法
- 4 基于高斯概率密度异常检测算法
- 5 Opprentice——异常检测经典算法最终篇
- 6 基于重构概率的 VAE 异常检测
- 7 基于条件VAE异常检测
- 8 Donut: 基于 VAE 的 Web 应用周期性 KPI 无监督异常检测
- 9 异常检测资料汇总(持续更新&抛砖引玉)
- 10 Bagel: 基于条件 VAE 的鲁棒无监督KPI异常检测
- 11 ADS: 针对大量出现的KPI流快速部署异常检测模型
- 12 Buzz: 对复杂 KPI 基于VAE对抗训练的非监督异常检测
- 13 MAD: 基于GANs的时间序列数据多元异常检测
- 14 对于流数据基于 RRCF 的异常检测
- 15 通过无监督和主动学习进行实用的白盒异常检测
- 16 基于VAE和LOF的无监督KPI异常检测算法
- 17 基于 VAE-LSTM 混合模型的时间异常检测
- 18 USAD:多元时间序列的无监督异常检测
- 19 OmniAnomaly:基于随机循环网络的多元时间序列鲁棒异常检测
- 20 HotSpot:多维特征 Additive KPI 的异常定位
- 21 Anomaly Transformer: 基于关联差异的时间序列异常检测
- 22 Kontrast: 通过自监督对比学习识别软件变更中的错误
- 23 TimesNet: 用于常规时间序列分析的时间二维变化模型
- 24 TSB-UAD:用于单变量时间序列异常检测的端到端基准套件
- 25 DIF:基于深度隔离林的异常检测算法
相关:
- VAE 模型基本原理简单介绍
- GAN 数学原理简单介绍以及代码实践
- 单指标时间序列异常检测——基于重构概率的变分自编码(VAE)代码实现(详细解释)
25. 基于深度隔离林的异常检测算法
论文名称:Deep Isolation Forest for Anomaly Detection
会议名称:IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING(TKDE)
下载地址:https://arxiv.org/abs/2206.06602
源码地址:https://github.com/xuhongzuo/deep-iforest
论文相关推荐阅读链接:https://zhuanlan.zhihu.com/p/625557221
请容许我感叹一下:本系列第1篇讲异常检测的算法时用到的就是 Isolation Forest,峰回路转,再次遇见。
25.1 论文概述
这篇论文的摘要部分介绍了他们提出的一种新的异常检测方法,称为深度隔离森林(Deep Isolation Forest)。该方法利用神经网络将原始数据映射到随机表示集合中,从而实现非线性分区和更好地隔离真正的异常值。与传统的隔离森林方法相比,深度隔离森林方法具有更高的检测准确性和更快的训练速度。作者还通过在多个数据集上进行实验验证了该方法的有效性。
解决方法关键思路:利用神经网络强大的表示能力将原始数据映射到一组新的数据空间中,并且通过在这些新创建的数据空间上执行简单的轴平行分割即可以很容易地实现非线性隔离(相当于在原始数据空间中不同大小的子空间上进行非线性分割)。
这篇论文的主要贡献包括:
-
引入了深度隔离森林(DIF)方法,该方法利用神经网络产生的随机表示来实现非线性数据空间的分区,从而有效地隔离真正的异常值。
-
提出了一种新的数据表示方案,利用随机表示集合和随机分区进行数据分割,从而在表格、图形和时间序列数据集上实现了显著的改进。
-
通过实验证明,深度隔离森林方法在异常检测任务中取得了显著的改进,同时也继承了隔离森林方法的良好可扩展性。
这些贡献使得深度隔离森林方法成为了异常检测领域的一个重要创新,为处理高维、非线性数据空间中的异常值提供了一种有效的解决方案。
个人意见,仅供参考:读论文时,先读标题,再读发表在哪个会议或期刊,再读Abstract 和 Introduction 中的 contribution,这些应该都比较容易理解,快速过一遍。
25.2 相关技术
由于隔离森林相对而言容易理解,并且在本系列课程的第一篇已经介绍,本篇不再重复介绍隔离森林相关内容。需要的小伙伴查阅相关资料自行学习。
这篇论文涉及的相关技术主要包括:
-
隔离森林(Isolation Forest):传统的异常检测方法之一,通过随机选择特征和随机切分数据来构建孤立树,从而实现对异常值的检测。
-
深度神经网络(Deep Neural Networks):用于生成随机表示集合的神经网络模型,通过非线性映射实现对原始数据的转换。
-
非线性数据分区:利用随机表示集合和随机分区进行数据分割,从而在高维、非线性数据空间中更好地隔离真正的异常值。
-
异常值评分函数:利用隐藏在映射密集表示中的定量信息和定性比较,实现对数据对象孤立难度的更准确评估,从而提高异常值评分的准确性。
根据论文的意思,这些技术的结合使得深度隔离森林方法能够在处理复杂数据集中的异常检测任务中取得显著的改进,并且具有良好的可扩展性和通用性。
在论文2.3节提到的 Deep Ensembles 是指深度集成模型,它是一种将多个独立训练的神经网络的预测结果进行组合的方法。这种方法可以提高预测准确性,并在不修改原始工作流程的情况下提供不确定性估计。与其他基于集成的方法类似,深度集成模型的质量很大程度上取决于其成员的多样性。尽管深度集成模型相对简单,但它仍然会带来相当大的计算成本。因此,许多相关研究试图解决这两个关键限制,例如通过使用排斥项来确保个体多样性,通过对抗性方式增加多样性,或者提出一种可以吸收尽可能多的功能多样性的精炼模型。此外,深度集成模型也启发了异常检测方面的相关研究,例如结合一组自动编码器并使用重构误差的中位数作为异常值得分。为了提高成员多样性,这些自动编码器是稀疏连接的。
因此,深度集成模型是一种利用多个独立训练的神经网络进行组合的方法,以提高预测准确性并提供不确定性估计。
25.3 核心方法
这篇论文的核心技术是深度隔离森林(DIF)方法。DIF方法利用神经网络产生的随机表示来实现非线性数据空间的分区,从而有效地隔离真正的异常值。与传统的隔离森林方法相比,DIF方法具有更高的检测准确性和更快的训练速度。DIF方法的关键在于利用深度神经网络生成随机表示集合,从而实现对原始数据的非线性映射,然后利用随机分区进行数据分割,从而在高维、非线性数据空间中更好地隔离真正的异常值。DIF方法的创新性在于将深度神经网络和隔离森林方法相结合,从而实现了对异常检测任务的显著改进。
接下来的内容主要从数学的角度描述一下论文方法,以下内容未严格按照论文先后顺序。
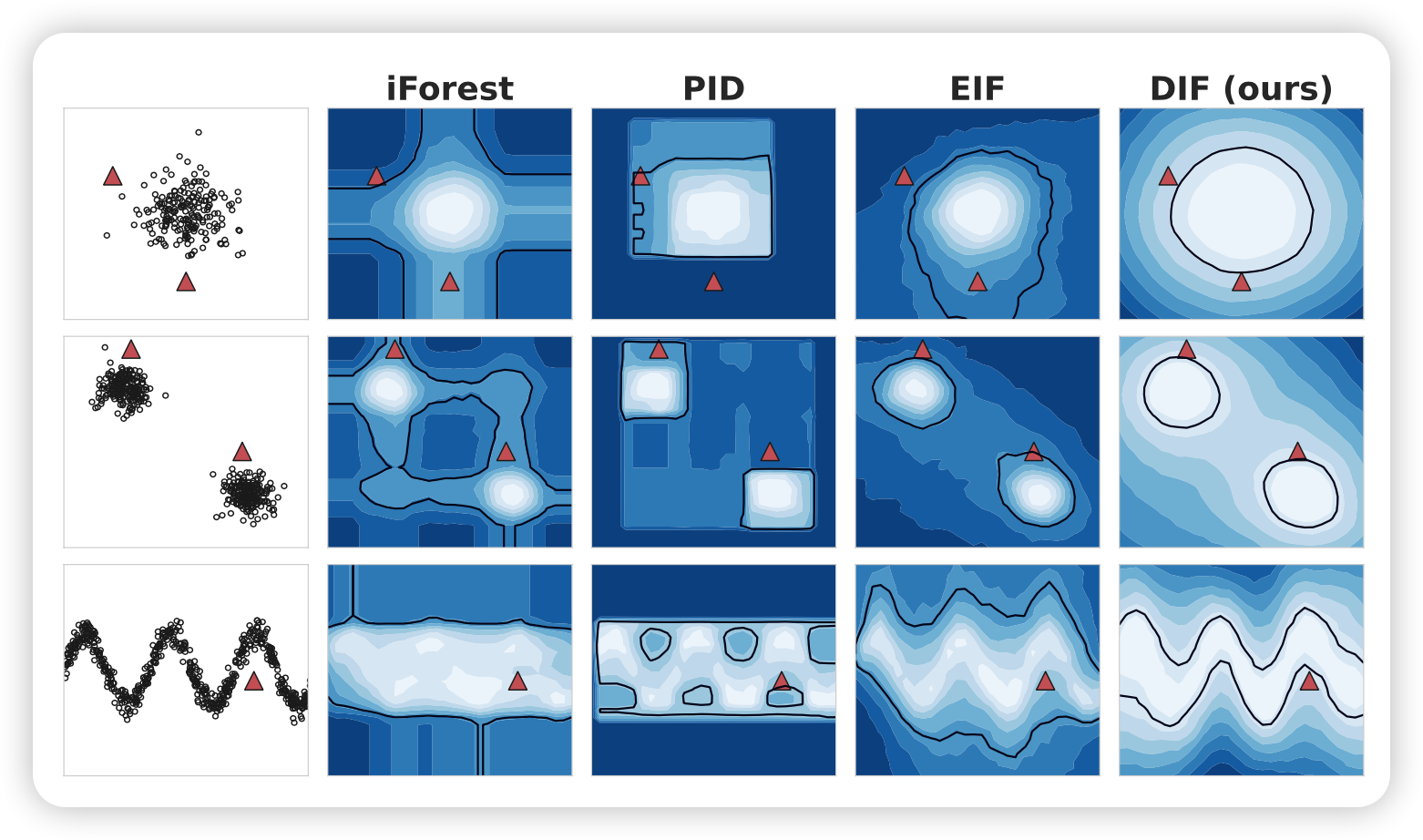
25.3.1 问题陈述和符号 PRELIMINARIES: ISOLATION FOREST
此部分论文主要提到了以下几个概念:
- 数据集: D \mathcal{D} D;
- 隔离树( iTree \textbf{iTree} iTree):用符号 T \mathcal{T} T 表示;隔离树的本质是二叉树,树中的每个节点对应一个数据对象池。一个包含 n n n 个数据对象的子集被用作根节点的数据池,根节点从整个数据集中随机下采样
- 隔离森林(\textbf{Isolation Forest):由许多隔离树组成的集成模型。隔离树是一种用于异常检测的树形结构,它通过对数据空间进行递归的随机划分来隔离异常值。每棵隔离树都是通过随机选择特征和随机阈值来构建的,从而形成了对数据空间的随机划分。在隔离树中,异常值通常比正常值更容易被隔离到树的较浅层,因此可以通过路径长度来评估数据点的异常程度。隔离森林则是由多棵隔离树组成的集成模型。每棵隔离树都是独立构建的,因此它们可以并行生成。隔离森林通过对每个数据点在每棵树中的路径长度进行平均,来得到最终的异常得分。由于隔离森林利用了多棵树的集成效果,因此通常能够更准确地识别异常值,并且相对于单棵隔离树,隔离森林对参数的选择更加鲁棒。
- 分割阈值: η \eta η
- 随机选择的索引: j j j
- 对象的第 j 维度特征: o ( j ) o^{(j)} o(j)
- 隔离森立中隔离树的数目: T T T
- 隔离森林的表示方法: T = { T i } i = 1 T \mathcal{T}=\{{\mathcal{T}_i\}}^T_{i=1} T={Ti}i=1T
- 数据对象的异常程度表示方法: ∣ p ( o ∣ T ) ∣ |p(o|\mathcal{T})| ∣p(o∣T)∣
- 数据对象 o 平局路径长度: E T i ∈ T ( ∣ p ( o ( T i ) ) ∣ ) \mathbb{E}_{\mathcal{T}_i \in \mathcal{T}}(|p(o(\mathcal{T}_i))|) ETi∈T(∣p(o(Ti))∣)
- 异常得分表示方法: F iFoerst ( o ∣ T ) = 2 − E τ i ∈ T ∣ p ( o ∣ τ i ) ∣ C ( T ) \mathscr{F}_{\text {iFoerst }}(\boldsymbol{o} \mid \mathcal{T})=2^{-\mathbb{E}_{\tau_i \in \mathcal{T}} \frac{\left|p\left(\boldsymbol{o} \mid \tau_i\right)\right|}{C(T)}} FiFoerst (o∣T)=2−Eτi∈TC(T)∣p(o∣τi)∣
iForest使用的是一种简单的隔离方法,即通过随机选择特征和随机阈值来构建隔离树。具体来说,对于一个数据集 D \mathcal{D} D,iForest首先随机选择一个特征 q q q 和一个阈值 p p p,然后将数据集 D \mathcal{D} D 分成两个子集 D l \mathcal{D}_l Dl 和 D r \mathcal{D}_r Dr,其中 D l \mathcal{D}_l Dl 包含所有特征 q q q 的值小于 p p p 的数据点, D r \mathcal{D}_r Dr 包含所有特征 q q q 的值大于等于 p p p 的数据点。这个过程可以表示为:
D l = { x ∈ D ∣ x q < p } D r = { x ∈ D ∣ x q ≥ p } \mathcal{D}_l = \{\mathbf{x} \in \mathcal{D} \mid x_q < p\} \\ \mathcal{D}_r = \{\mathbf{x} \in \mathcal{D} \mid x_q \geq p\} Dl={x∈D∣xq<p}Dr={x∈D∣xq≥p}
然后,iForest递归地对子集 D l \mathcal{D}_l Dl 和 D r \mathcal{D}_r Dr 进行相同的操作,直到达到停止条件。停止条件可以是树的深度达到预定值,或者子集中只包含一个数据点。
在隔离树中,数据点的异常得分可以通过路径长度来计算。具体来说,对于一个数据点 x \mathbf{x} x,它在隔离树中的路径长度 h ( x ) h(\mathbf{x}) h(x) 可以表示为:
h ( x ) = E ( h ( x , T ) ) h(\mathbf{x}) = E(h(\mathbf{x}, T)) h(x)=E(h(x,T))
其中 T T T 是隔离树, h ( x , T ) h(\mathbf{x}, T) h(x,T) 是数据点 x \mathbf{x} x 在隔离树 T T T 中的路径长度, E ( ⋅ ) E(\cdot) E(⋅) 表示对随机选择的树进行平均。在隔离森林中,数据点的异常得分是所有隔离树中路径长度的平均值。
25.3.2 深度隔离森林 DEEP ISOLATION FOREST
DIF首先通过无优化神经网络产生随机表示集成,定义为
G ( D ) = { X u ⊂ R d ∣ X u = ϕ u ( D ; θ u ) } u = 1 r (1) \mathscr{G}(\mathcal{D})=\left\{\mathcal{X}_u \subset \mathbb{R}^d \mid \mathcal{X}_u=\phi_u\left(\mathcal{D} ; \theta_u\right)\right\}_{u=1}^r \tag{1} G(D)={Xu⊂Rd∣Xu=ϕu(D;θu)}u=1r(1)
其中 r r r 是指集合的大小, ϕ u : D ↦ R d \phi_u: \mathcal{D} \mapsto \mathbb{R}^d ϕu:D↦Rd 是将原始数据映射到新的 d d d 维空间的网络,对 θ u \theta_u θu 中的网络权值进行随机初始化。 每个表示用 t t t 树赋值,构造包含 T = r × t T=r\times t T=r×t棵隔离数的隔离森林 T = { τ i } i = 1 T \mathcal{T}=\left\{\tau_i\right\}_{i=1}^T T={τi}i=1T 。 X \mathcal{X} X 的 iTree 由一组投影数据 P 1 ⊂ X \mathcal{P}_1 \sub \mathcal{X} P1⊂X 的根节点初始化。数据池中的第 k k k 个结点 P k \mathcal{P_k} Pk 分支成两个叶节点与不相交的子集,即 P 2 k = { x ∣ x ( j k ) ≤ η k , x ∈ P k } \mathcal{P_{2k}} = \{x | x^{(j_k)} \le \eta_k, x \in \mathcal{P_k}\} P2k={x∣x(jk)≤ηk,x∈Pk} 并且 P 2 k + 1 = { x ∣ x ( j k ) > η k , x ∈ P k } \mathcal{P}_{2 k+1}=\left\{\boldsymbol{x} \mid \boldsymbol{x}^{\left(j_k\right)}>\eta_k, \boldsymbol{x} \in \mathcal{P}_k\right\} P2k+1={x∣x(jk)>ηk,x∈Pk},其中 j k j_k jk 是在新创建的数据空间 { 1 , . . . , d } \{1,...,d\} {1,...,d}的所有维度中均匀随机地选择, x ( j k ) \boldsymbol{x}^{\left(j_k\right)} x(jk) 为预测数据对象的第 j j j 维, η k \eta_k ηk 为 { x ( j k ) ∣ x ∈ P k } \{\boldsymbol{x}^{\left(j_k\right)}\mid x\in\mathcal{P_k}\} {x(jk)∣x∈Pk} 范围内的分割值。
构造 T \mathcal{T} T 后,根据 tForest 每个 iTree 的隔离困难程度来评估数据对象 o o o 的异常程度,评分函数定义为
F ( o ∣ T ) = Ω τ i ∼ T I ( o ∣ τ i ) (2) \mathscr{F}(\boldsymbol{o} \mid \mathcal{T})=\Omega_{\tau_i \sim \mathcal{T}} I\left(\boldsymbol{o} \mid \tau_i\right) \tag{2} F(o∣T)=Ωτi∼TI(o∣τi)(2)
式中, I ( o ∣ τ i ) I\left(\boldsymbol{o} \mid \tau_i\right) I(o∣τi) 表示iTree τ i \tau_i τi中 隔离困难度的函数, Ω \Omega Ω 表示积分函数。
25.3.3 深度隔离森林的实现 Implementation of DIF
Deep Isolation Forest (DIF)的实现过程主要包括以下几个步骤:
-
随机表示集合的生成:DIF利用随机初始化的神经网络将原始数据映射到随机表示集合中。每个表示都是由一个神经网络生成的,网络权重是随机初始化的。这种随机表示集合的生成方式使得DIF能够进行非线性分区,从而更好地处理复杂数据集中的困难异常。
-
隔离树的构建:对于每个随机表示,DIF使用隔离树(iTree)进行隔离。隔离树是一种二叉树结构,其中每个节点都是一个随机选择的特征和一个随机选择的分割点。通过对数据进行递归分割,隔离树可以将数据划分为不同的区域,从而实现对异常数据的隔离。
-
集成隔离树:DIF将每个随机表示的隔离树集成成一个隔离森林。这种集成方式可以提高隔离的准确性和鲁棒性,从而更好地发现真实异常。
-
异常评分:最后,DIF使用隔离森林对新数据进行异常评分。对于新数据,DIF将其在每个随机表示下的路径长度进行平均,得到一个综合的异常评分。这个评分可以用来判断数据是否为异常数据。
总的来说,DIF的实现过程主要包括随机表示集合的生成、隔离树的构建、集成隔离树和异常评分。这种方法利用随机初始化的神经网络进行数据表示,实现了非线性分区和更好的隔离效果,从而在异常检测方面取得了显著的改进。
DIF中有两个主要组成部分,即随机表示集成函数 G \mathscr{G} G 和基于隔离的异常评分函数 F \mathscr{F} F。为了提高表示函数 G \mathscr{G} G 的时间效率,我们提出了计算效率的深度表示集成方法 (Computation-Efficient deep Representation Ensemble method, CERE)。该算法可以在给定的小批量中同时计算所有集合成员。为了进一步提高异常评分的准确性,我们提出了偏差增强异常评分函数(Deviation-Enhanced Anomaly Scoring function,DEAS),通过利用投影密集表示中隐藏的定量信息,并进行定性比较。
CERE:计算高效的深度表示集成方法 (Computation-Efficient deep Representation Ensemble) 是Deep Isolation Forest(DIF)中的一个重要组成部分,旨在提高表示集成的计算效率。CERE的实现过程主要包括以下几个步骤:
-
并行计算:为了提高表示集成的计算效率,CERE利用并行计算的方式,同时在给定的小批量数据上计算所有的集成成员。这种并行计算方式能够充分利用计算资源,大大减少计算时间和内存开销。
-
利用计算加速器:CERE充分利用计算加速器(如GPU)进行小批量计算,以进一步提高计算效率。通过利用计算加速器的并行计算能力,CERE能够高效地生成表示集成,从而加速整个DIF方法的执行过程。
总的来说,CERE通过并行计算和计算加速器的利用,实现了计算高效的深度表示集成方法。这种方法能够大大减少表示集成的计算时间和内存开销,提高DIF方法的执行效率,从而更好地应用于实际的异常检测任务中。
DEAS:偏差增强异常评分功能 (Deviation-Enhanced Anomaly Scoring) 是Deep Isolation Forest(DIF)中的关键组成部分,旨在提高异常评分的准确性。DEAS的实现过程主要包括以下几个步骤:
-
利用密集表示中的隐藏定量信息:DEAS利用神经网络生成的密集表示中的隐藏定量信息,结合定性比较,提高异常评分的准确性。这些隐藏定量信息可以包括数据对象的特征值之间的关系以及分支阈值等,这些信息可以提供更多的数据隔离难度的定量信息。
-
定性比较:除了利用隐藏定量信息,DEAS还进行定性比较,以进一步提高异常评分的准确性。通过对每个节点进行定性比较,DEAS能够更好地评估数据对象的隔离难度,从而提高异常评分的质量。
总的来说,DEAS通过利用密集表示中的隐藏定量信息和定性比较,提高了异常评分的准确性。这种方法能够更准确地评估数据对象的隔离难度,从而提高DIF方法的异常检测性能。
25.3.4 DIF 算法 Algorithm of DIF
算法1:构建深度隔离树
该算法是隔离树的构建过程,其中输入为数据集
D
D
D,输出为隔离树
τ
\tau
τ。在算法中,首先初始化隔离树的根节点,并将数据集
D
D
D 分配给该节点。然后,对于每个节点,随机选择一个特征和一个分割点,将数据集分成左右两个子集,并将每个子集分配给一个新的内部节点。然后,递归地对左右子树进行相同的操作,直到达到树的最大深度
h
h
h 或子集中只有一个数据点。最后,将外部节点附加到当前节点并返回隔离树。

算法2:偏差增强异常评分
描述了使用偏差增强方法计算异常评分的过程。该算法概述了将数据对象转换为矢量化表示、初始化隔离树以及基于遍历路径和累积差异计算异常分数的步骤。
1.输入:输入数据集由需要计算异常分数的数据对象组成。
2.转换:将数据对象转换为矢量化表示,表示为
x
u
{x}_u
xu,使用指定的方法。
3.初始化:该算法初始化隔离树和转换后的数据对象的子集,以进行异常评分。
4.遍历和路径记录:每个数据对象遍历每个隔离树,遍历路径
p
(
x
u
∣
τ
i
)
{p}({x}_u|\tau_i)
p(xu∣τi)和累积差值
{
β
}
{\beta}
{β}。
5.异常分数计算:路径长度
∣
p
(
x
u
∣
τ
i
)
∣
{|p}({x}_u|\tau_i)|
∣p(xu∣τi)∣和偏差
g
(
x
u
∣
τ
i
)
{g}({x}_u|\tau_i)
g(xu∣τi)。
6.聚合:根据记录的遍历路径和累积的差异计算每个数据对象的异常分数。
7.输出:该算法基于偏差增强方法返回输入数据对象的异常分数。
该算法为将基于偏差的异常评分纳入隔离林框架提供了一种系统的方法,允许对数据集中的异常程度进行更细致的评估。

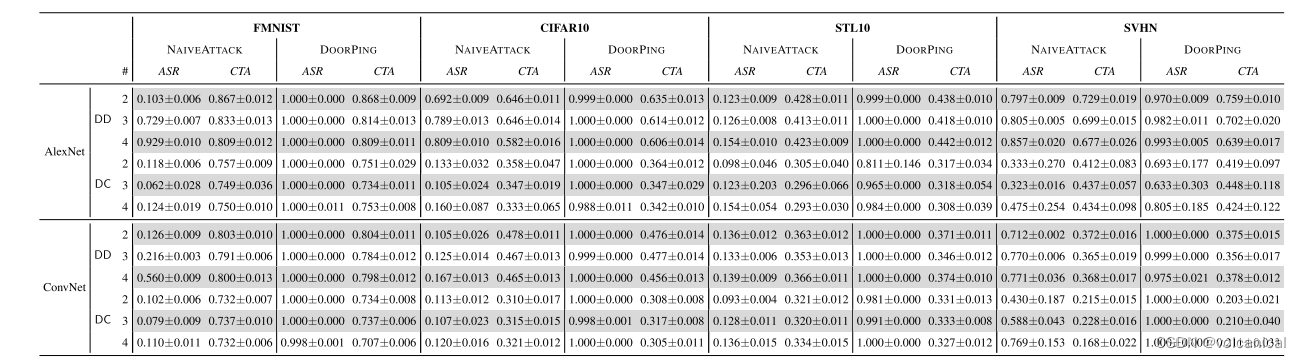
25.5 论文实验
这里我们不去看原论文实验过程与实验结果了,只是跑跑源码,看看效果。
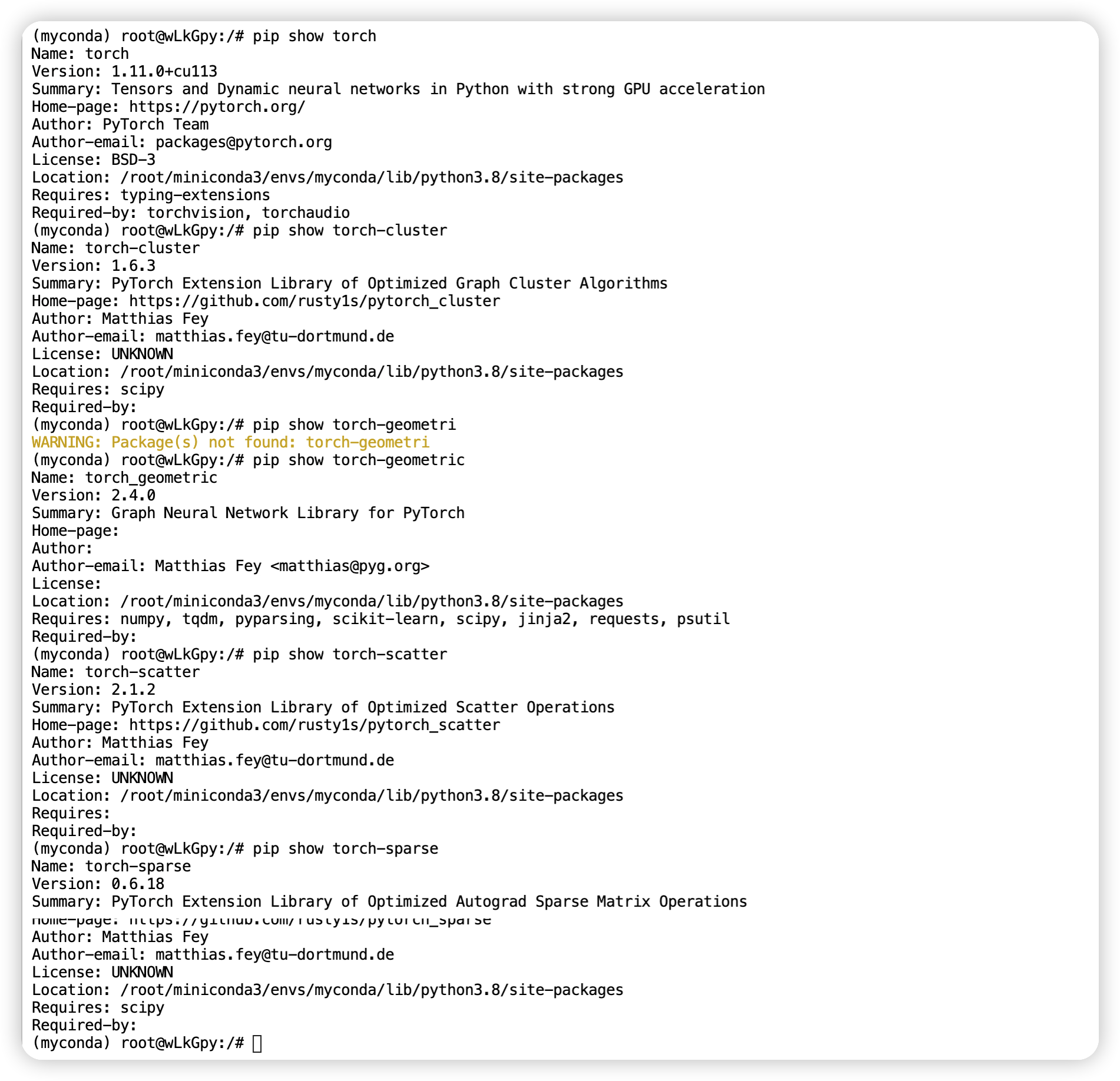
这个过程中最麻烦的就是环境搭建,我们首先把源码中的 requirements.txt 修改如下:
pandas==1.3.3
numpy==1.20.3
networkx==2.6.3
scikit-learn==0.24.2
torch
torch-cluster
torch-geometric
torch-scatter
torch-sparse
tqdm==4.62.3
注意看一下自己已经安装的版本是否 “大致符合要求” 。比如源码中要求 torch 版本为 torch==1.10.1+cu113 ,我实际的版本为 1.11.0+cu113。其他的也类似地比较一下。
安装依赖过程:

安装完成以后查看关键依赖的版本。
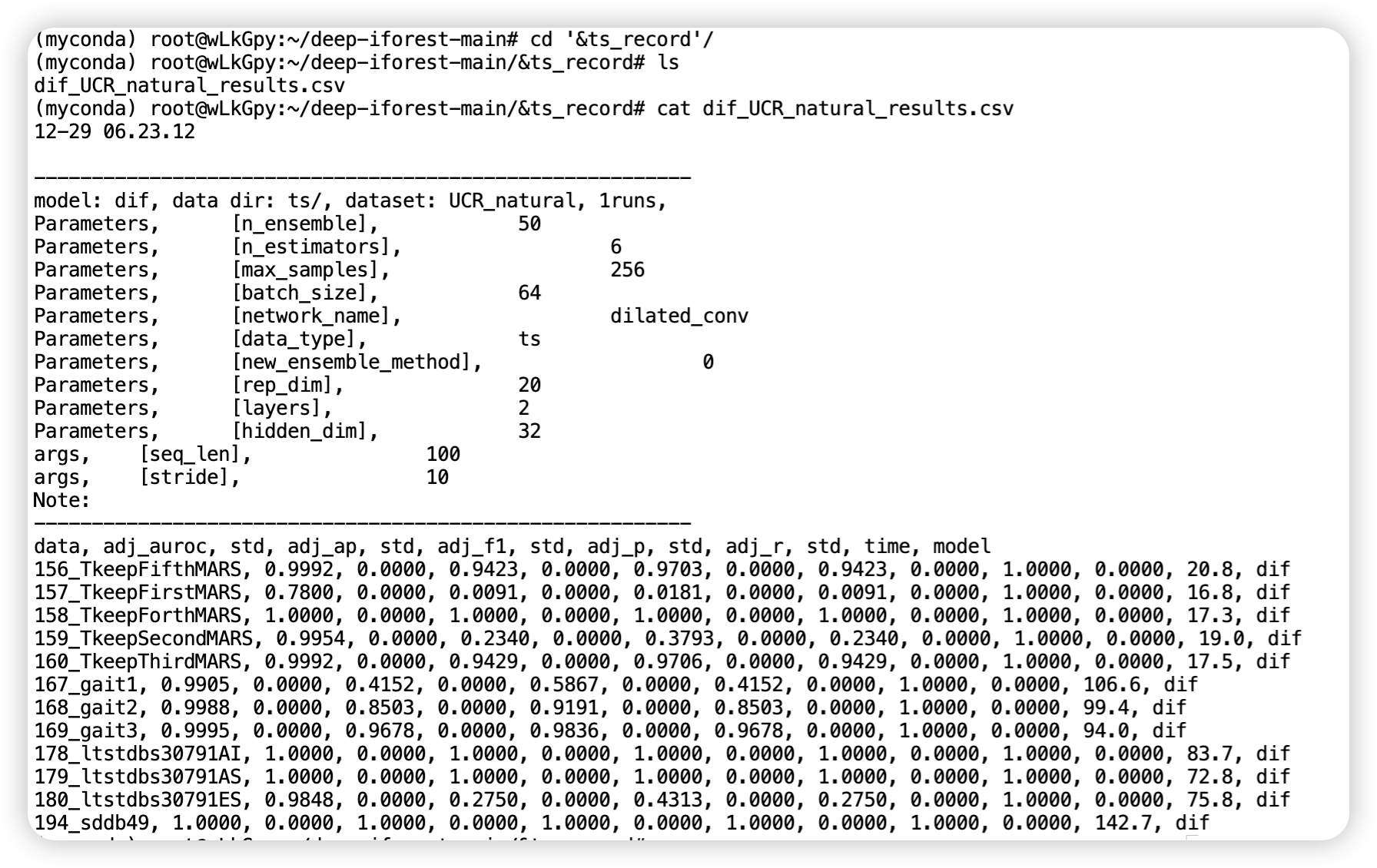
运行 main_ts.py 文件,全部都使用默认参数。
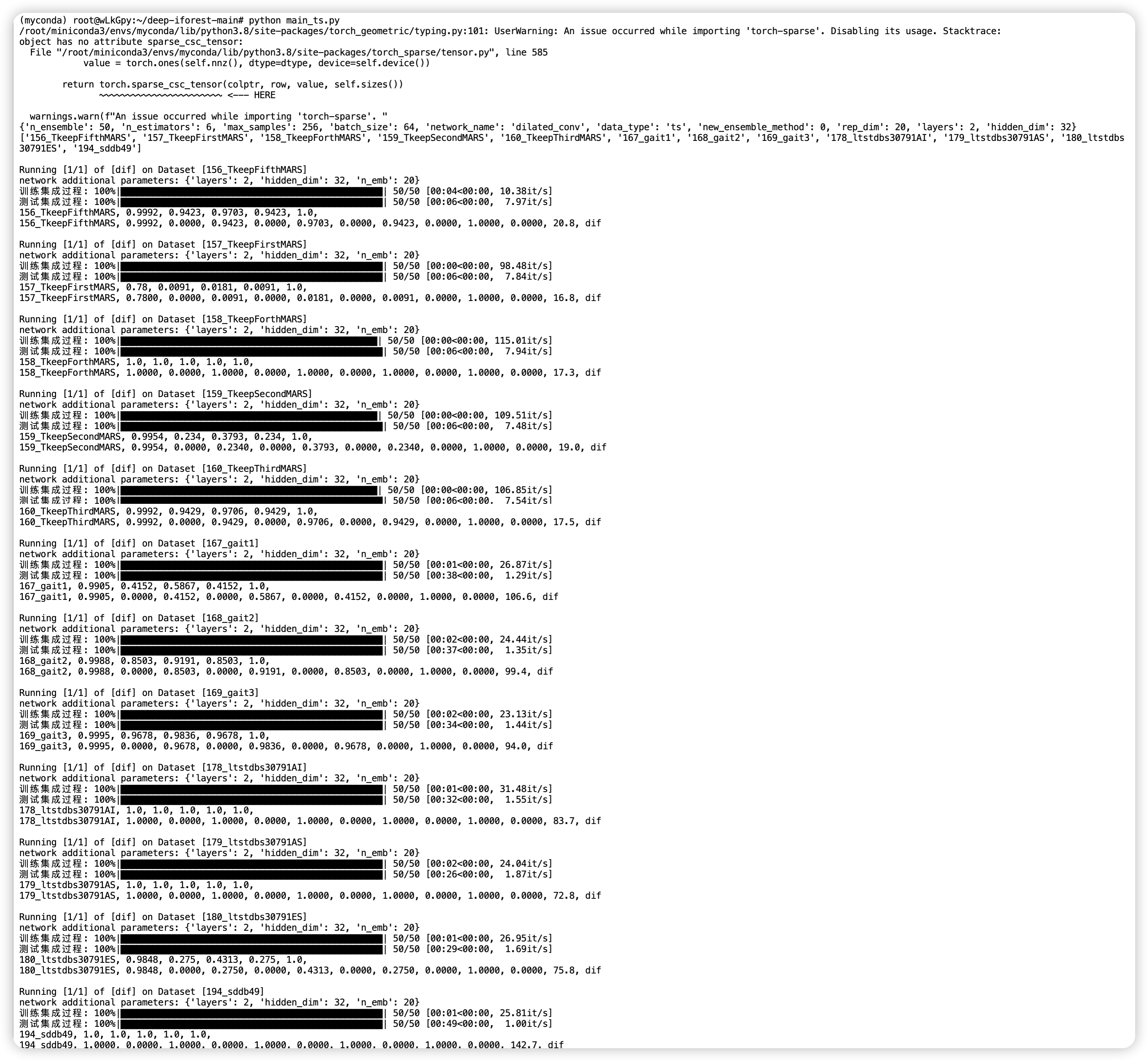
结合源码理解运行过程中输出的内容。
180_ltstdbs30791ES, 0.9848, 0.275, 0.4313, 0.275, 1.0,
180_ltstdbs30791ES, 0.9848, 0.0000, 0.2750, 0.0000, 0.4313, 0.0000, 0.2750, 0.0000, 1.0000, 0.0000, 75.8, dif
其中,adj_f1 的平均值为 0.9848,标准差为 0.275。这表示在该次运行中,对于数据集 “180_ltstdbs30791ES”,模型的 F1 分数有一定的波动。adj_f1 的平均值告诉你模型在这个数据集上的平均性能,而标准差告诉你这些运行中 F1 分数的变异程度。
最终也会输出一个 csv 文件,不妨查看一下。
25.6 速读源码
源码主要关注两个 py 文件,分别是 algorithms/dif.py 以及 algorithms/net_torch.py,源码注释比较详细,推荐直接前去阅读。
25.6.1 DIF
接下来我们按照函数为基本单位,对各个部分进行简单介绍。
class DIF:
"""初始化模型,传入一堆参数"""
def __init__(self, network_name='mlp', network_class=None,
n_ensemble=50, n_estimators=6, max_samples=256,
hidden_dim=[500,100], rep_dim=20, skip_connection=None, dropout=None, activation='tanh',
data_type='tabular', batch_size=64,
new_score_func=True, new_ensemble_method=True,
random_state=42, device='cuda', n_processes=1,
verbose=0, **network_args):
.....
"""fit过程初始化模型属性"""
def fit(self, X, y=None):
......
"""使用拟合的检测器预测X的原始异常分数。基于不同的检测器算法来计算输入样本的异常分数。为了一致性,异常值被分配较大的异常分数。"""
def decision_function(self, X):
.......
def _training_transfer(self, X, ensemble_seeds):
"""
训练深度集成模型。
Args:
X: 输入数据。
ensemble_seeds: 包含用于初始化集成模型的种子值的列表。
Returns:
None
"""
if self.new_ensemble_method:
# 新的集成方法
# 使用第一个种子值设置随机种子
self.set_seed(ensemble_seeds[0])
# 创建神经网络模型,使用Net类,并传递指定的参数
net = self.Net(n_features=self.n_features, **self.network_args).to(self.device)
# 初始化网络模型
self.net_init(net)
# 使用深度传递批量集成方法处理输入数据
self.x_reduced_lst = self.deep_transfer_batch_ensemble(X, net)
# 将初始化的模型添加到列表中
self.net_lst.append(net)
else:
# 旧的集成方法
# 遍历每次集成迭代
for i in tqdm(range(self.n_ensemble), desc='训练集成过程', ncols=100, leave=None):
# 为这次迭代设置随机种子
self.set_seed(ensemble_seeds[i])
# 创建神经网络模型,使用Net类,并传递指定的参数
net = self.Net(n_features=self.n_features, **self.network_args).to(self.device)
# 初始化网络模型
self.net_init(net)
# 使用深度传递方法处理输入数据
self.x_reduced_lst.append(self.deep_transfer(X, net))
# 将初始化的模型添加到列表中
self.net_lst.append(net)
# 方法结束,没有明确的返回值(返回None)
return
def _inference_transfer(self, X):
"""
推断方法,用于生成测试数据的降维表示。
Args:
X: 测试数据。
Returns:
生成的测试数据的降维表示列表。
"""
# 检查特殊情况
if self.data_type == 'tabular' and X.shape[0] == self.x_reduced_lst[0].shape[0]:
# 如果数据类型为'tabular'且测试数据行数与之前训练集的行数相同,直接返回之前训练集的降维表示
return self.x_reduced_lst
else:
# 否则,创建一个空的列表,用于存储新的测试数据的降维表示
test_reduced_lst = []
# 根据是否使用新的集成方法进行不同的处理
if self.new_ensemble_method:
# 使用新的集成方法
# 对测试数据进行降维表示
test_reduced_lst = self.deep_transfer_batch_ensemble(X, self.net_lst[0])
else:
# 未使用新的集成方法
# 遍历每个训练好的模型,对测试数据进行降维表示
for i in tqdm(range(self.n_ensemble), desc='测试集成过程', ncols=100, leave=None):
x_reduced = self.deep_transfer(X, self.net_lst[i])
# 将结果添加到列表中
test_reduced_lst.append(x_reduced)
# 返回生成的测试数据的降维表示列表
return test_reduced_ls
def _inference_scoring(self, x_reduced_lst, n_processes):
"""
推断得分方法,用于生成模型的得分。
Args:
x_reduced_lst: 降维表示列表。
n_processes: 并行处理的进程数。
Returns:
最终得分列表。
"""
# 根据是否使用新的得分函数选择得分函数
if self.new_score_func:
score_func = self.single_predict
else:
score_func = self.single_predict_abla
# 获取样本数量
n_samples = x_reduced_lst[0].shape[0]
# 初始化得分列表
self.score_lst = np.zeros([self.n_ensemble, n_samples])
# 单进程处理
if n_processes == 1:
for i in range(self.n_ensemble):
# 使用得分函数计算得分
scores = score_func(x_reduced_lst[i], self.clf_lst[i])
self.score_lst[i] = scores
else:
# 多进程处理
start = np.arange(0, self.n_ensemble, np.ceil(self.n_ensemble / n_processes))
for j in range(int(np.ceil(self.n_ensemble / n_processes))):
run_id = start + j
run_id = np.array(np.delete(run_id, np.where(run_id >= self.n_ensemble)), dtype=int)
if self.verbose >= 1:
print('多进程运行的集成ID:', run_id)
# 使用进程池进行并行计算
pool = Pool(processes=n_processes)
process_lst = [pool.apply_async(score_func, args=(x_reduced_lst[i], self.clf_lst[i]))
for i in run_id]
pool.close()
pool.join()
# 将计算结果填充回得分列表
for rid, process in zip(run_id, process_lst):
self.score_lst[rid] = process.get()
# 计算最终得分,取各模型得分的平均值
final_scores = np.average(self.score_lst, axis=0)
return final_scores
def deep_transfer(self, X, net):
"""
深度转移方法,用于对输入数据进行降维表示。
Args:
X: 输入数据。
net: 训练好的神经网络模型。
Returns:
降维表示结果。
"""
x_reduced = []
# 在无梯度计算的上下文中执行
with torch.no_grad():
# 根据数据类型选择不同的 DataLoader
if self.data_type != 'graph':
# 非图数据的 DataLoader
loader = DataLoader(X, batch_size=self.batch_size, drop_last=False, pin_memory=True, shuffle=False)
for batch_x in loader:
# 将批次数据转换为张量,并移动到设备上
batch_x = batch_x.float().to(self.device)
# 使用神经网络模型进行降维计算
batch_x_reduced = net(batch_x)
x_reduced.append(batch_x_reduced)
else:
# 图数据的 DataLoader(使用 pyG 的 DataLoader)
loader = pyGDataLoader(X, batch_size=self.batch_size, shuffle=False, pin_memory=True, drop_last=False)
for data in loader:
# 将图数据移动到设备上
data.to(self.device)
x, edge_index, batch = data.x, data.edge_index, data.batch
# 处理缺失特征
if x is None:
x = torch.ones((batch.shape[0], 1)).to(self.device)
# 使用神经网络模型进行降维计算
x, _ = net(x, edge_index, batch)
x_reduced.append(x)
# 将结果转换为 NumPy 数组,并进行标准化和激活函数处理
x_reduced = torch.cat(x_reduced).data.cpu().numpy()
x_reduced = StandardScaler().fit_transform(x_reduced)
x_reduced = np.tanh(x_reduced)
return x_reduced
# 其他部分有注释或比较容易理解
25.6.2 net_torch
以下代码均摘录自论文源码,并根据自己的理解添加了一些注释,希望可以帮助到小伙伴们。
# -*- coding: utf-8 -*-
# Implementation of Neural Networks in PyTorch
# @Time : 2022/8/19
# @Author : Xu Hongzuo (hongzuo.xu@gmail.com)
import numpy as np
import torch
import torch_geometric
from torch.nn import functional as F
def choose_net(network_name):
"""
根据给定的网络名称返回相应的神经网络模型类。
Args:
network_name (str): 神经网络模型的名称。
Returns:
对应网络名称的神经网络模型类。
"""
if network_name == 'mlp':
return MLPnet
elif network_name == 'gru':
return GRUNet
elif network_name == 'lstm':
return LSTMNet
elif network_name == 'gin':
return GinEncoderGraph
elif network_name == 'dilated_conv':
return DilatedConvEncoder
else:
raise NotImplementedError("")
def choose_act_func(activation):
"""
根据给定的激活函数名称返回相应的激活函数模块和激活函数函数。
Args:
activation (str): 激活函数的名称。
Returns:
包含激活函数模块和激活函数函数的元组。
"""
if activation == 'relu':
act_module = torch.nn.ReLU()
act_f = torch.relu
elif activation == 'leaky_relu':
act_module = torch.nn.LeakyReLU()
act_f = F.leaky_relu
elif activation == 'tanh':
act_module = torch.nn.Tanh()
act_f = torch.tanh
elif activation == 'sigmoid':
act_module = torch.nn.Sigmoid()
act_f = torch.sigmoid
else:
raise NotImplementedError('')
# 返回包含激活函数模块和激活函数函数的元组
return act_module, act_f
def choose_pooling_func(pooling):
"""
根据给定的池化方法名称返回相应的全局池化函数。
Args:
pooling (str): 池化方法的名称。
Returns:
全局池化函数。
"""
if pooling == 'sum':
pool_f = torch_geometric.nn.global_add_pool
elif pooling == 'mean':
pool_f = torch_geometric.nn.global_mean_pool
elif pooling == 'max':
pool_f = torch_geometric.nn.global_max_pool
else:
raise NotImplementedError('')
return pool_f
class MLPnet(torch.nn.Module):
def __init__(self, n_features, n_hidden=[500, 100], n_emb=20, activation='tanh',
skip_connection=None, dropout=None, be_size=None):
"""
初始化 MLP 网络模型。
Args:
n_features (int): 输入特征的维度。
n_hidden (list or int or str): 隐藏层的维度,可以是一个包含每个隐藏层维度的列表,也可以是一个整数,或者是一个逗号分隔的字符串。
n_emb (int): 输出特征的维度(嵌入维度)。
activation (str): 激活函数的名称,支持 'relu', 'tanh', 'sigmoid', 'leaky_relu'。
skip_connection (str or None): 跳连接方式,可以是 'concat' 或 None。
dropout (float or None): Dropout 概率,可以为 None。
be_size (int or None): 重复输入的倍数,可以为 None。
Notes:
- 如果 n_hidden 是一个整数,将其视为隐藏层的维度。
- 如果 n_hidden 是一个字符串,将其解析为逗号分隔的整数列表。
"""
super(MLPnet, self).__init__()
self.skip_connection = skip_connection
self.n_emb = n_emb
assert activation in ['relu', 'tanh', 'sigmoid', 'leaky_relu']
# 处理 n_hidden,确保其为列表形式
if type(n_hidden) == int:
n_hidden = [n_hidden]
elif type(n_hidden) == str:
n_hidden = n_hidden.split(',')
n_hidden = [int(a) for a in n_hidden]
num_layers = len(n_hidden)
self.be_size = be_size
self.layers = []
for i in range(num_layers + 1):
in_channels, out_channels = self.get_in_out_channels(i, num_layers, n_features,
n_hidden, n_emb, skip_connection)
self.layers += [LinearBlock(in_channels, out_channels,
activation=activation if i != num_layers else None,
skip_connection=skip_connection if i != num_layers else 0,
dropout=dropout,
be_size=be_size)]
self.network = torch.nn.Sequential(*self.layers)
def forward(self, x):
"""
前向传播。
Args:
x: 输入数据。
Returns:
网络输出。
"""
if self.be_size is not None:
x = x.repeat(self.be_size, 1)
x = self.network(x)
return x
def get_in_out_channels(self, i, num_layers, n_features, n_hidden, n_emb, skip_connection):
"""
获取每一层的输入通道数和输出通道数。
Args:
i (int): 当前层的索引。
num_layers (int): 隐藏层的总数。
n_features (int): 输入特征的维度。
n_hidden (list): 隐藏层的维度列表。
n_emb (int): 输出特征的维度(嵌入维度)。
skip_connection (str or None): 跳连接方式。
Returns:
in_channels (int): 输入通道数。
out_channels (int): 输出通道数。
"""
if skip_connection is None:
in_channels = n_features if i == 0 else n_hidden[i - 1]
out_channels = n_emb if i == num_layers else n_hidden[i]
elif skip_connection == 'concat':
in_channels = n_features if i == 0 else np.sum(n_hidden[:i]) + n_features
out_channels = n_emb if i == num_layers else n_hidden[i]
else:
raise NotImplementedError('')
return in_channels, out_channels
class AEnet(torch.nn.Module):
def __init__(self, n_features, n_hidden=[500, 100], n_emb=20, activation='tanh',
skip_connection=None, be_size=None):
"""
初始化自动编码器(Autoencoder)神经网络模型。
Args:
n_features (int): 输入特征的维度。
n_hidden (list or int or str): 隐藏层的维度,可以是一个包含每个隐藏层维度的列表,也可以是一个整数,或者是一个逗号分隔的字符串。
n_emb (int): 嵌入维度,即编码的特征维度。
activation (str): 激活函数的名称,支持 'tanh', 'relu'。
skip_connection (str or None): 跳连接方式,可以是 None。
be_size (int or None): 重复输入的倍数,可以为 None。
Notes:
- 如果 n_hidden 是一个整数,将其视为隐藏层的维度。
- 如果 n_hidden 是一个字符串,将其解析为逗号分隔的整数列表。
"""
super(AEnet, self).__init__()
assert activation in ['tanh', 'relu']
# 处理 n_hidden,确保其为列表形式
if type(n_hidden) is int:
n_hidden = [n_hidden]
elif type(n_hidden) is str:
n_hidden = n_hidden.split(',')
n_hidden = [int(a) for a in n_hidden]
num_layers = len(n_hidden)
self.be_size = be_size
# 编码器(Encoder)部分
self.encoder_layers = []
for i in range(num_layers + 1):
in_channels = n_features if i == 0 else n_hidden[i - 1]
out_channels = n_emb if i == num_layers else n_hidden[i]
self.encoder_layers += [LinearBlock(in_channels, out_channels,
bias=False,
activation=activation if i != num_layers else None,
skip_connection=None,
be_size=be_size)]
# 解码器(Decoder)部分
self.decoder_layers = []
for i in range(num_layers + 1):
in_channels = n_emb if i == 0 else n_hidden[num_layers - i]
out_channels = n_features if i == num_layers else n_hidden[num_layers - 1 - i]
self.decoder_layers += [LinearBlock(in_channels, out_channels,
bias=False,
activation=activation if i != num_layers else None,
skip_connection=None,
be_size=be_size)]
self.encoder = torch.nn.Sequential(*self.encoder_layers)
self.decoder = torch.nn.Sequential(*self.decoder_layers)
def forward(self, x):
"""
前向传播。
Args:
x: 输入数据。
Returns:
enc (tensor): 编码后的特征。
xx (tensor): 解码后的输出。
x (tensor): 输入数据。
"""
if self.be_size is not None:
x = x.repeat(self.be_size, 1)
# 编码过程
enc = self.encoder(x)
# 解码过程
xx = self.decoder(enc)
return enc, xx, x
class LinearBlock(torch.nn.Module):
"""
Linear layer block with support of concatenation-based skip connection and batch ensemble
Parameters
----------
in_channels: int
input dimensionality
out_channels: int
output dimensionality
bias: bool (default=False)
bias term in linear layer
activation: string, choices=['tanh', 'sigmoid', 'leaky_relu', 'relu'] (default='tanh')
the name of activation function
skip_connection: string or None, default=None
'concat' use concatenation to implement skip connection
dropout: float or None, default=None
the dropout rate
be_size: int or None, default=None
the number of ensemble size
"""
def __init__(self, in_channels, out_channels,
bias=False, activation='tanh',
skip_connection=None, dropout=None, be_size=None):
super(LinearBlock, self).__init__()
self.act = activation
self.skip_connection = skip_connection
self.dropout = dropout
self.be_size = be_size
if activation is not None:
self.act_layer, _ = choose_act_func(activation)
if dropout is not None:
self.dropout_layer = torch.nn.Dropout(p=dropout)
if be_size is not None:
bias = False
self.ri = torch.nn.Parameter(torch.randn(be_size, in_channels))
self.si = torch.nn.Parameter(torch.randn(be_size, out_channels))
self.linear = torch.nn.Linear(in_channels, out_channels, bias=bias)
def forward(self, x):
# 如果存在集成大小
if self.be_size is not None:
# 生成重复的参数矩阵以匹配输入大小
R = torch.repeat_interleave(self.ri, int(x.shape[0] / self.be_size), dim=0)
S = torch.repeat_interleave(self.si, int(x.shape[0] / self.be_size), dim=0)
# 使用集成参数进行线性变换,并在结果上应用逐元素乘法
x1 = torch.mul(self.linear(torch.mul(x, R)), S)
else:
# 普通线性变换
x1 = self.linear(x)
# 如果定义了激活函数,则应用激活函数
if self.act is not None:
x1 = self.act_layer(x1)
# 如果定义了 dropout,则应用 dropout
if self.dropout is not None:
x1 = self.dropout_layer(x1)
# 如果定义了跳跃连接为 'concat',则将输入和输出连接在一起
if self.skip_connection == 'concat':
x1 = torch.cat([x, x1], axis=1)
return x1
class GRUNet(torch.nn.Module):
"""
使用 GRU 网络的模块。
参数
----------
n_features: int
输入特征的数量
hidden_dim: int, default=20
隐藏层的维度
layers: int, default=1
GRU 层的数量
"""
def __init__(self, n_features, hidden_dim=20, layers=1):
super(GRUNet, self).__init__()
self.gru = torch.nn.GRU(n_features, hidden_size=hidden_dim, batch_first=True, num_layers=layers)
def forward(self, x):
# GRU 前向传播
_, hn = self.gru(x)
# 返回最后一个时间步的隐藏状态
return hn[-1]
class LSTMNet(torch.nn.Module):
"""
使用 LSTM 网络的模块。
参数
----------
n_features: int
输入特征的数量
hidden_dim: int, default=20
隐藏层的维度
layers: int, default=1
LSTM 层的数量
bidirectional: bool, default=False
是否使用双向 LSTM
"""
def __init__(self, n_features, hidden_dim=20, layers=1, bidirectional=False):
super(LSTMNet, self).__init__()
self.bi = bidirectional
self.lstm = torch.nn.LSTM(n_features, hidden_size=hidden_dim, batch_first=True,
bidirectional=bidirectional, num_layers=layers)
def forward(self, x):
# LSTM 前向传播
output, (hn, c) = self.lst
class SamePadConv(torch.nn.Module):
"""
具有相同 padding 的卷积模块。
参数
----------
in_channels: int
输入通道数
out_channels: int
输出通道数
kernel_size: int
卷积核大小
dilation: int, default=1
卷积核的扩张率
groups: int, default=1
分组卷积中的组数
"""
def __init__(self, in_channels, out_channels, kernel_size, dilation=1, groups=1):
super().__init__()
# receptive_field
self.receptive_field = (kernel_size - 1) * dilation + 1
# 计算 padding
padding = self.receptive_field // 2
# 创建卷积层
self.conv = torch.nn.Conv1d(
in_channels, out_channels, kernel_size,
padding=padding,
dilation=dilation,
groups=groups
)
# 如果 receptive_field 为偶数,需要去掉一列输出
self.remove = 1 if self.receptive_field % 2 == 0 else 0
def forward(self, x):
# 前向传播
out = self.conv(x)
# 如果receptive_field为偶数,去掉一列输出
if self.remove > 0:
out = out[:, :, : -self.remove]
return out
class ConvBlock(torch.nn.Module):
"""
卷积块模块,包含两个相同 padding 的卷积层和可选的投影层。
参数
----------
in_channels: int
输入通道数
out_channels: int
输出通道数
kernel_size: int
卷积核大小
dilation: int
卷积核的扩张率
final: bool, default=False
是否为最后一层卷积块,如果是,则添加投影层
"""
def __init__(self, in_channels, out_channels, kernel_size, dilation, final=False):
super().__init__()
# 第一个卷积层
self.conv1 = SamePadConv(in_channels, out_channels, kernel_size, dilation=dilation)
# 第二个卷积层
self.conv2 = SamePadConv(out_channels, out_channels, kernel_size, dilation=dilation)
# 如果不是最后一层卷积块,添加投影层
self.projector = torch.nn.Conv1d(in_channels, out_channels, 1) if in_channels != out_channels or final else None
def forward(self, x):
# 记录残差
residual = x if self.projector is None else self.projector(x)
# 使用 GELU 激活函数
x = F.gelu(x)
# 第一个卷积层
x = self.conv1(x)
# 使用 GELU 激活函数
x = F.gelu(x)
# 第二个卷积层
x = self.conv2(x)
# 返回结果加上残差
return x + residual
class DilatedConvEncoder(torch.nn.Module):
"""
膨胀卷积编码器模块,包含输入全连接层、膨胀卷积块序列和表示丢弃层。
参数
----------
n_features: int
输入特征的维度
hidden_dim: int, default=20
隐藏层维度
n_emb: int, default=20
输出嵌入的维度
layers: int, default=1
膨胀卷积块的层数
kernel_size: int, default=3
卷积核大小
"""
def __init__(self, n_features, hidden_dim=20, n_emb=20, layers=1, kernel_size=3):
super().__init__()
# 输入全连接层
self.input_fc = torch.nn.Linear(n_features, hidden_dim)
# 通道数序列
channels = [hidden_dim] * layers + [n_emb]
# 膨胀卷积块序列
self.net = torch.nn.Sequential(*[
ConvBlock(
channels[i - 1] if i > 0 else hidden_dim,
channels[i],
kernel_size=kernel_size,
dilation=2 ** i,
final=(i == len(channels) - 1)
)
for i in range(len(channels))
])
# 表示丢弃层
self.repr_dropout = torch.nn.Dropout(p=0.1)
def forward(self, x):
# 输入全连接层
x = self.input_fc(x)
# 调整维度
x = x.transpose(1, 2) # B x Ch x T
# 膨胀卷积块序列
x = self.net(x)
# 调整维度
x = x.transpose(1, 2)
# 表示丢弃层
x = self.repr_dropout(x)
# 最大池化层
x = F.max_pool1d(
x.transpose(1, 2),
kernel_size=x.size(1)
).transpose(1, 2).squeeze(1)
return x
## 后面的基本上差不多,不同的网络而已
25.7 总结
- 论文介绍了一种新的表征范式,即随机表征集成,与传统的认知方式有所不同。
- 通常,神经网络需要设定一个训练目标以进行优化,然后生成最优的表征。然而,在这个方法中,神经网络不再需要优化或设定学习目标,而是提出了一种全新的随机表征集成的表征方式。
- 这一新方法的优势在于其表征范式中的随机性,这赋予了在原始数据空间中进行高度自由划分的能力,并激发了随机表征与下游基于随机划分的孤立操作之间的独特协同效应。
- 该方法有助于有效孤立难例异常,消除算法偏差,从而显著提高检测性能。
- 由于这种前向传播较为耗时,论文还提出了一种高效深度表征集成方法,即CERE(Cumulative Embedding REpresentation)。CERE方法的核心思想是使用两个向量的乘积来生成Rank-1矩阵,作为神经网络参数矩阵。这使得在一次前向传播中能够同时计算所有集成成员,提高计算效率。
Smileyan
2023.12.29 20:08