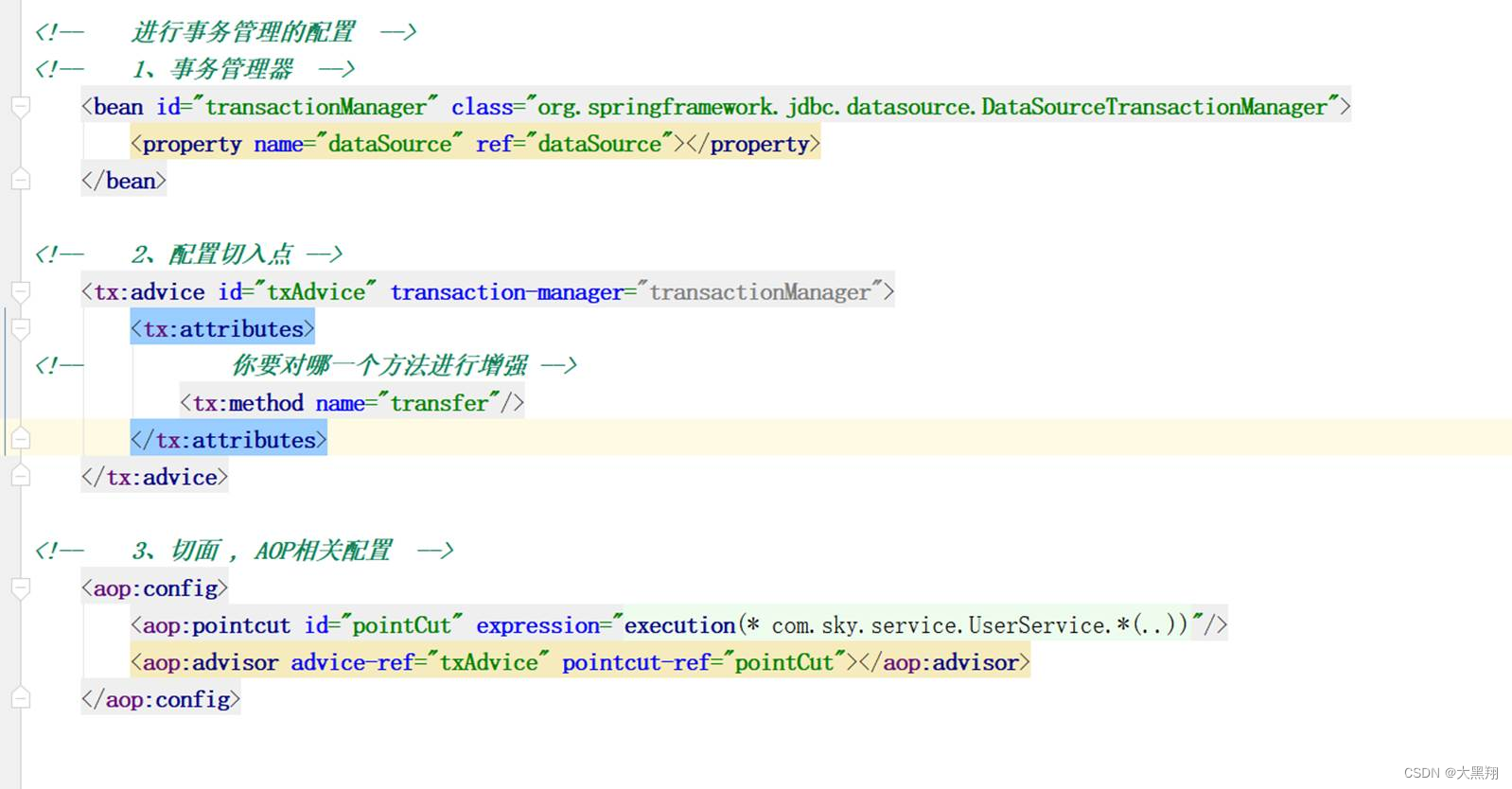
搜索插入位置

给定一个有序数组nums，数组中没有重复元素。搜索指定元素target在数组中插入位置。题目说如果target存在于数组中，直接返回index，如果不在返回应该插入的位置。要求在O（logn）的时间复杂度内完成。

因为是有序数组，题目很简单。
思路： 从索引0开始，把数组的元素和target比较，如果比target小，就继续比较下一个索引位置的元素，直到元素等于或大于target，返回该索引。

class Solution {
    public int searchInsert(int[] nums, int target) {

        int i = 0;

        while( i < nums.length){
            
            if( nums[i] < target){
                i ++;
            }else if( nums[i] == target){
                break;
            }else{
                break;
            }
        }

        return i; 

    }
}

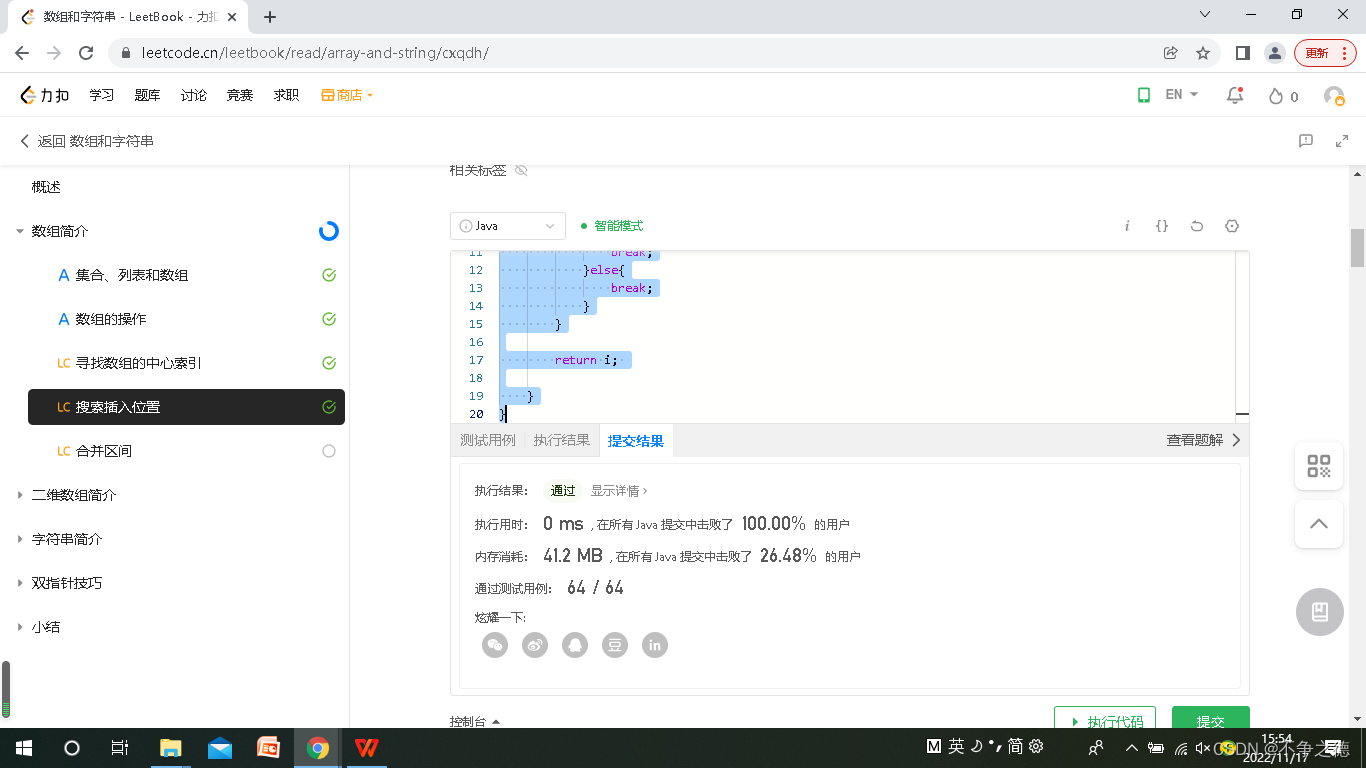
内存貌似消耗稍微多了一点。那么就优化一下代码吧，其实我们无需区别元素存在于不存在，因为要反馈的索引并没有实质变化。

优化后的代码

class Solution {
    public int searchInsert(int[] nums, int target) {

        int i = 0;

        while( i < nums.length){
            
            if( nums[i] < target){
                i ++;
            }else{
                break;
            }
        }

        return i; 

    }
}

优化后，内存消耗减少了0.3MB。

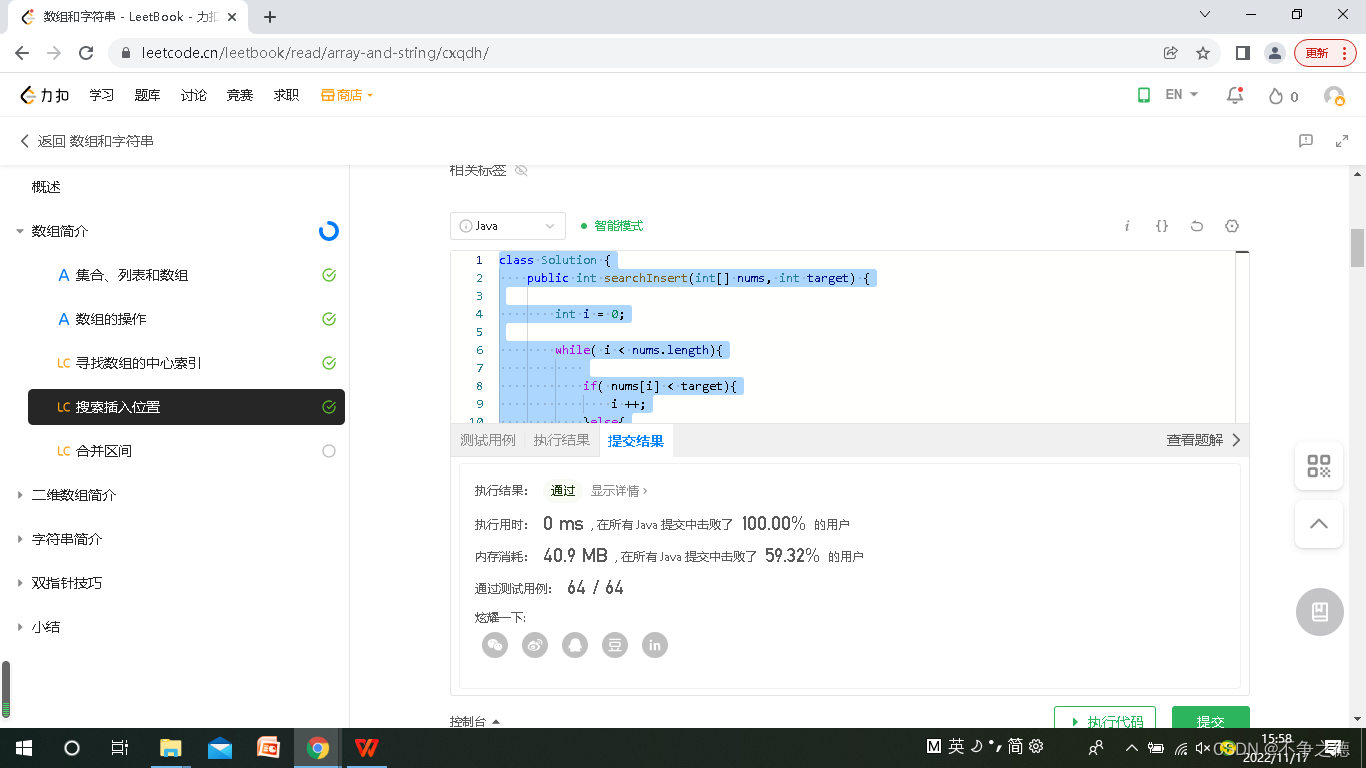
用for循环也可以实现。

class Solution {
    public int searchInsert(int[] nums, int target) {

        int i = 0;
        for ( ;i < nums.length;i++){
            
            if( nums[i] >= target){            
                break;
            }
        }
        return i; 
    }
}

我其实很好奇for和while在资源消耗上有什么不同，所以修改成for循环之后，我又提交了，发现消耗了41MB内存，但是我随后又提交了多次，每次都不一样， 总体上都在41MB以上，我可以理解为for循环比while循环消耗的内存稍微多一些吗？

关于时间复杂度

这道题O（logn)是没有问题的。
其实计算时间复杂度也是挺值得研究的问题，这个O（logn）的复杂度我理解就是一个模拟的估算值，就任何一次计算而言，都可能是不一样的，具体的值取决于n和target的情况。

我其实很懒，不喜欢推导公式，就不累自己了。简单说，target和nums的元素的情况决定了循环里是否需要遍历所有元素。最好的情况就是不用遍历，第一个元素就是target或者比target大，那么就直接跳出循环返回index。 最差的情况就是最后一个元素也比target小，那么就要遍历整个数组，最后返回index。可能更常见的情况是，遍历数组的一部分元素。那么，这个时间复杂度O（logn)体现的是随机模拟多次实验后得到的时间复杂度的整体评估值，我猜实验得到了一条对数曲线。

大体上，我觉得，只有一个循环结构，并且不必要遍历所有元素的程序，时间复杂度都是O（logn）。