引言

上一节介绍了使用前向后向算法求解基于链式条件随机场中某隐状态的边缘概率分布，本节将介绍条件随机场中模型参数的学习任务。

回顾：条件随机场求解边缘概率分布

场景设计

条件随机场使用的数据集合是一个序列信息。以词性标注为例，已知数据集合$\mathcal{X}$以及对应的序列标注标签$\mathcal{Y}$表示如下：
其中$T$表示序列长度。
X = { x ( 1 ) , x ( 2 ) , ⋯   , x ( N ) } Y = { y ( 1 ) , y ( 2 ) , ⋯   , y ( N ) } x ( i ) , y ( i ) ∈ R T ; i = 1 , 2 , ⋯   , N \begin{aligned} \mathcal X = \{x^{(1)},x^{(2)},\cdots,x^{(N)}\} \\ \mathcal Y = \{y^{(1)},y^{(2)},\cdots,y^{(N)}\} \\ x^{(i)},y^{(i)} \in \mathbb R^T;i=1,2,\cdots,N \end{aligned} X={x(1),x(2),⋯,x(N)}Y={y(1),y(2),⋯,y(N)}x(i),y(i)∈RT;i=1,2,⋯,N​
推断任务中的边缘概率分布的求解问题即：模型给定的条件下，对于陌生样本序列$x_{1:T}$，求解其词性标注序列某一时刻结果$y_t$的条件概率：
这里设定隐状态的取值是‘离散型随机变量’，如[名词,动词,形容词,副词,...],它的取值集合用$\mathcal{K}$表示。
P ( y t = j ∣ x 1 : T ) { t ∈ { 1 , 2 , ⋯ T } j ∈ K = { 1 , 2 , ⋯   , K } \mathcal P(y_t=j \mid x_{1:T}) \begin{cases} t \in \{1,2,\cdots T\} \\ j \in \mathcal K = \{1,2,\cdots,\mathcal K\} \end{cases} P(yt​=j∣x1:T​){t∈{1,2,⋯T}j∈K={1,2,⋯,K}​

前向后向算法

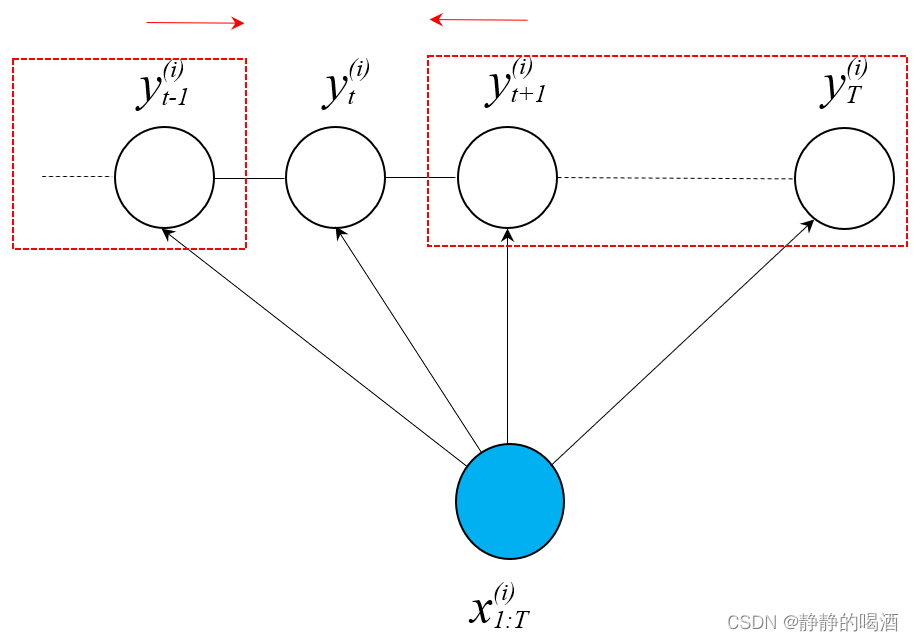
前向后向算法(Forward-Backward Algorithm)对应概率图模型描述表示如下：

将$\mathcal{P}(y_t\mid x_{1:T})$的因子分解求解过程划分为两部分：
其中$\mathcal{Z}$表示配分函数~
$$\begin{array}{rl}\mathcal{P}(y_t\mid x_{1:T})& =\sum _{y_1,\cdots ,y_{t-1}}\sum _{y_{t+1},\cdots ,y_T}\frac{1}{\mathcal{Z}}\prod _{t=1}^{T-1}{\psi }_t(y_t,y_{t+1},x_{1:T})\\ & =\frac{1}{\mathcal{Z}}\left[\sum _{y_1,\cdots y_{t-1}}\prod _{i=1}^{t-1}{\psi }_i(y_i,y_{i+1},x_{1:T})\right]\cdot \left[\sum _{y_{t+1},\cdots ,y_T}\prod _{i=t}^{T-1}{\psi }_i(y_i,y_{i+1},x_{1:T})\right]\\ & =\frac{1}{\mathcal{Z}}{\Delta }_{left}\cdot {\Delta }_{right}\end{array}$$
对于链式条件随机场，无论前向还是后向，它们都可以用变量消去法(Variable Elimination,VE)的方式进行化简：
$$\begin{array}{rl}{\Delta }_{left}={\alpha }_t(k)& =\sum _{y_{t-1}}{\psi }_{t-1}(y_{t-1},y_t=k,x_{1:T})\cdots \sum _{y_2}{\psi }_2(y_2,y_3,x_{1:T})\sum _{y_1}{\psi }_1(y_1,y_2,x_{1:T})\\ {\Delta }_{right}={\beta }_t(m)& =\sum _{y_{t+1}}{\psi }_t(y_t=m,y_{t+1},x_{1:T})\sum _{y_{t+2}}{\psi }_{t+1}(y_{t+1},y_{t+2},x_{1:T})\cdots \sum _{y_T}{\psi }_{T-1}(y_{T-1},y_T,x_{1:T})\end{array}$$

关于条件随机场的学习任务

在条件随机场要解决的任务中介绍了学习任务本质是求解最优模型参数$\hat{\theta }$，而判别标准是$\mathcal{P}(\mathcal{Y}\mid \mathcal{X})$：
集合$\mathcal{X},\mathcal{Y}$中的各样本均服从‘独立同分布’。
$$\begin{array}{rl}\hat{\theta }& =\underset{\theta }{\mathrm{argmax}}\mathcal{P}(\mathcal{Y}\mid \mathcal{X})\\ & =\underset{\theta }{\mathrm{argmax}}\prod _{i=1}^N\mathcal{P}(y^{(i)}\mid x^{(i)})\end{array}$$
在建模对象的表示中，模型参数$\theta$共包含两个部分：$\lambda ,\eta$。它门分别表示转移特征函数$s(y_{t+1},y_t,x_{1:T})$和状态特征函数$g(y_t,x_{1:T})$的参数信息。
$$\begin{array}{rlr}\theta & =(\lambda ,\eta {)}^T& =({\lambda }_1,\cdots ,{\lambda }_{\mathcal{M}},{\eta }_1,\cdots ,{\eta }_{\mathcal{L}}{)}^T\end{array}$$
对应建模对象$\mathcal{P}(y\mid x)$表示如下：
其中$\mathcal{P}(y\mid x)$中$x,y$分别表示数据集合$\mathcal{X}$中的任意样本以及对应标注信息，这里$x$和$x_{1:T}$等价。
$$\mathcal{P}(y\mid x)=\frac{1}{\mathcal{Z}(x_{1:T},\lambda ,\eta )}\exp \left[{\lambda }^T\sum _{t=1}^{T-1}s(y_t,y_{t+1},x_{1:T})+{\eta }^T\sum _{t=1}^{T}g(y_t,x_{1:T})\right]$$
对最优参数$\hat{\theta }$进行细分，并将$x^{(i)},y^{(i)}$代入有：
在展开过程中加入一个$log$,和极大似然估计的思路相同，$log$函数不影响函数的单调性，因而不影响最优参数的选择。
$$\begin{array}{rl}\hat{\theta }\Rightarrow \hat{\lambda },\hat{\eta }& =\underset{\lambda ,\eta }{\mathrm{argmax}}\prod _{i=1}^N\mathcal{P}(y^{(i)}\mid x^{(i)})\\ & \Rightarrow \underset{\lambda ,\eta }{\mathrm{argmax}}\left[\log \prod _{i=1}^N\mathcal{P}(y^{(i)}\mid x^{(i)})\right]\\ & =\underset{\lambda ,\eta }{\mathrm{argmax}}\sum _{i=1}^N\log \mathcal{P}(y^{(i)}\mid x^{(i)})\\ & =\underset{\lambda ,\eta }{\mathrm{argmax}}\sum _{i=1}^N\log \left\{\frac{1}{\mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )}\exp \left[{\lambda }^T\sum _{t=1}^{T-1}s(y_t^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})+{\eta }^T\sum _{t=1}^{T}g(y_t^{(i)},x_{1:T}^{(i)})\right]\right\}\end{array}$$
继续对上式进行展开，有：
$\log$和$\exp$消掉了~
$$\begin{array}{rl}\hat{\lambda },\hat{\eta }& =\underset{\lambda ,\eta }{\mathrm{argmax}}\sum _{i=1}^N\left[\log \frac{1}{\mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )}+\log \exp \left({\lambda }^T\sum _{t=1}^{T-1}s(y_t^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})+{\eta }^T\sum _{t=1}^{T}g(y_t^{(i)},x_{1:T}^{(i)})\right)\right]\\ & =\underset{\lambda ,\eta }{\mathrm{argmax}}\sum _{i=1}^N\left[-\log \mathcal{Z}\left(x_{1:T}^{(i)},\lambda ,\eta \right)+{\lambda }^T\sum _{t=1}^{T-1}s(y_t^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})+{\eta }^T\sum _{i=1}^{T}g(y_t^{(i)},x_{1:T}^{(i)})\right]\end{array}$$
定义目标函数$\mathcal{J}(\lambda ,\eta ,x_{1:T}^{(i)})$表示如下：
$$\begin{gathered} \mathcal{J}(\lambda ,\eta ，x_{1:T}^{(i)})=\sum _{i=1}^N\left[-\log \mathcal{Z}\left(x_{1:T}^{(i)},\lambda ,\eta \right)+{\lambda }^T\sum _{t=1}^{T-1}s(y_t^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})+{\eta }^T\sum _{i=1}^{T}g(y_t^{(i)},x_{1:T}^{(i)})\right] \\ \hat{\lambda },\hat{\eta }=\underset{\lambda ,\eta }{\mathrm{argmax}}\mathcal{J}(\lambda ,\eta ,x_{1:T}^{(i)}) \end{gathered}$$
针对 最大化问题，常用的方法：梯度上升(Gradient Ascent)。

• 需要针对目标函数$\mathcal{J}$关于$\lambda ,\eta$求解梯度：
  $$\begin{array}{r}{\nabla }_{\lambda }\mathcal{J}(\lambda ,\eta ,x_{1:T}^{(i)}),{\nabla }_{\eta }(\lambda ,\eta ,x_{1:T}^{(i)})\end{array}$$
• 模型参数在迭代过程中向梯度方向变化，从而逼近最优解：
  $$\begin{array}{r}{\lambda }^{(k+1)}={\lambda }^k+d_{\lambda }\cdot {\nabla }_{\lambda }\mathcal{J}({\lambda }^{(k)},{\eta }^{(k)},x_{1:T}^{(i)})\\ {\eta }^{(k+1)}={\eta }^k+d_{\eta }\cdot {\nabla }_{\eta }\mathcal{J}({\lambda }^{(k)},{\eta }^{(k)},x_{1:T}^{(i)})\end{array}$$

关于模型参数$\lambda$求解梯度

以求解$\lambda$为例，求解步骤如下：

梯度求解

求解梯度${\nabla }_{\lambda }\mathcal{J}(\lambda ,\eta ,x_{1:T}^{(i)})$：
观察$\mathcal{J}(\lambda ,\eta ,x_{1:T}^{(i)})$,其中${\sum }_{i=1}^T{\eta }^{T}g(y_t^{(i)},x_{1:T}^{(i)})$与$\lambda$无关。同理，对$\eta$求解梯度${\nabla }_{\eta }\mathcal{J}(\lambda ,\eta ,x_{1:T}^{(i)})$过程中，${\sum }_{t=1}^{T-1}{\lambda }^{T}s(y_t^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})$与$\eta$无关，本文仅对$\lambda$进行梯度求解。
$$\begin{array}{r}{\nabla }_{\lambda }\mathcal{J}(\lambda ,\eta ,x_{1:T}^{(i)})=\sum _{i=1}^N\left[\sum _{t-1}^{T-1}s(y_t^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})-{\nabla }_{\lambda }\log \mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )\right]\end{array}$$
其中$\log \mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )$被称作对数配分函数(log Partition Function)。最早在指数族分布介绍中出现的概念。在指数族分布——充分统计量与模型参数关系中介绍了 对数配分函数的导数与充分统计量之间的关联关系：
$$\begin{array}{rl}{\mathcal{A}}^{\prime }(\eta )=\frac{\partial \mathcal{A}(\eta )}{\partial \eta }& ={\int }_x\frac{1}{e^{\mathcal{A}(\eta )}}\cdot h(x)e^{{\eta }^T\varphi (x)}\cdot \varphi (x)dx\\ & ={\int }_x\mathcal{P}(x\mid \eta )\cdot \varphi (x)dx\\ & ={\mathbb{E}}_{\mathcal{P}(x\mid \eta )}[\varphi (x)]\end{array}$$
其中，$\mathcal{A}(\eta )$表示对数配分函数；$\varphi (x)$表示样本$x$的充分统计量；$\mathcal{P}(x\mid \eta )$（也有写作$\mathcal{P}(x;\eta )$） 表示$x$服从的概率分布。
需要注意的是：

• 在条件随机场的学习任务中将‘对数配分函数’写成$\log \mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )$的形式，但实际上，$x_{1:T}^{(i)}$仅表示已知的观测变量(样本数据)，并不是‘对数配分函数’的变量，变量只有$\lambda ,\eta$两个。
• 在‘建模对象’$\mathcal{P}(y^{(i)}\mid x^{(i)})$中，某一具体样本$x^{(i)}$的充分统计量该如何表示？回顾‘建模对象’$\mathcal{P}(y\mid x)$的展开式：
  $$\begin{array}{rl}\mathcal{P}(y\mid x)& =\frac{1}{\mathcal{Z}(x_{1:T},\lambda ,\eta )}\exp \left[{\lambda }^T\sum _{t=1}^{T-1}s(y_t,y_{t+1},x_{1:T})+{\eta }^T\sum _{t=1}^{T}g(y_t,x_{1:T})\right]\\ & =\left\{\frac{1}{\mathcal{Z}(x_{1:T},\lambda ,\eta )}\exp \left[{\lambda }^T\left(\sum _{t=1}^{T-1}s(y_t,y_{t+1},x_{1:T})\right)\right]\right\}\cdot \exp \left[{\eta }^T\sum _{t=1}^{T}g(y_t,x_{1:T})\right]\end{array}$$
  观察，由于条件随机场依然使用‘最大熵模型’作为底层逻辑，因此能够看出， { \{ {大括号$\}$中的项就是‘最大熵模型’的描述形式。而最大熵模型的定义式就是从‘指数族分布’的定义式演化而来。详见最大熵定理与指数族分布的关系。因此，充分统计量就是${\sum }_{t=1}^{T-1}s(y_t,y_{t+1},x_{1:T})$.
• 即便找到了充分统计量，并没有结束。因为我们要找的是$x_{1:T}^{(i)}$这个样本的充分统计量。在这里自然是对‘隐状态’$y_t,y_{t+1}$进行统计。看看$y_t,y_{t+1}$具体代表什么：
  $$\begin{gathered} y_t={\left(y_t^{(1)},y_t^{(2)},\cdots ,y_t^{(N)}\right)}^T \\ {y}_{t+1}={\left(y_{t+1}^{(1)},y_{t+1}^{(2)},\cdots ,y_{t+1}^{(N)}\right)}^T \end{gathered}$$
  通过上式，可以发现，统计的对象就是‘所有样本’在$t,t+1$时刻的‘离散取值结果’，并进行统计。具体是怎么统计的，这并不是我们关注的重点。$x_{1:T}^{(i)}$样本的‘充分统计量’表示如下：
  $$\varphi (x_{1:T}^{(i)})=\sum _{t=1}^{T-1}s(y_t,y_{t+1},x_{1:T}^{(i)})$$
  说了这么多，这里最重要的点即：$y_t,y_{t+1}$右上角没有样本编号，它表示所有样本$t,t+1$时刻的隐状态集合，它和上面‘建模对象中的’$y_t,y_{t+1}$不是一个东西。建模对象的$y_t,y_{t+1}$中的$y$表示样本集合$\mathcal{X}$任意一个样本$x$对应的标注序列。

将对数配分函数的导数结果带入，有：
个人理解：在整个隐状态分布下求解期望。
$${\nabla }_{\lambda }\left[\log \mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )\right]={\mathbb{E}}_{\mathcal{Y}}\left[\sum _{t=1}^{T-1}s(y_t,y_{t+1},x_{1:T}^{(i)})\right]\mathcal{Y}=(y_1,\cdots ,y_T{)}^T$$
接下来对上述期望结果进行求解：
$$\begin{array}{r}{\mathbb{E}}_{\mathcal{Y}}\left[\sum _{t=1}^{T-1}s(y_t,y_{t+1},x_{1:T}^{(i)})\right]=\sum _{\mathcal{Y}}\mathcal{P}(\mathcal{Y}\mid x_{1:T}^{(i)})\left[\sum _{t=1}^{T-1}f(y_t,y_{t+1},x_{1:T}^{(i)})\right]\end{array}$$
观察一下计算该式的时间复杂度：$\mathcal{Y}$包含$y_1,\cdots ,y_T$，并且每一个隐状态$y_t(t=1,2,\cdots ,T)$包含$|\mathcal{K}|$个取值，因此时间复杂度为：
$$O(|\mathcal{K}{|}^T)\cdot O(T-1)=O[(T-1)|\mathcal{K}{|}^T]$$
可以看出，这个复杂度是指数级别的，极难求解。

梯度的简化过程

观察上式，$\mathcal{Y}$和单个的$t$无关，因此将${\sum }_{\mathcal{Y}}\mathcal{P}(\mathcal{Y}\mid x_{1:T}^{(i)})$看成整体，${\sum }_{t=1}^{T-1}$提到前面：
$${\nabla }_{\lambda }\left[\log \mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )\right]=\sum _{t=1}^{T-1}\left[\sum _{\mathcal{Y}}\mathcal{P}(\mathcal{Y}\mid x_{1:T}^{(i)})s(y_t,y_{t+1},x_{1:T}^{(i)})\right]$$
将${\sum }_{\mathcal{Y}}$拆成三部分：
$$\sum _{\mathcal{Y}}=\sum _{y_1,\cdots ,y_T}=\sum _{y_1,\cdots ,y_{t-1}}\sum _{y_t,y_{t+1}}\sum _{y_{t+2},\cdots ,y_T}$$
交换一下顺序，最终结果表示如下：
其中，中括号中的项可以使用‘概率密度积分’的方式积分掉$\mathcal{Y}$中的$y_1,\cdots ,y_{t-1},y_{t+2},\cdots ,y_T$，只剩下$y_t,y_{t+1}$两项：
$$\begin{array}{rl}\sum _{y_1,\cdots ,y_{t-1}}\sum _{y_{t+2},\cdots ,y_T}\mathcal{P}(\mathcal{Y}\mid x_{1:T}^{(i)})& =\sum _{y_1,\cdots ,y_{t-1}}\sum _{y_{t+2},\cdots ,y_T}\mathcal{P}(y_1,y_2,\cdots ,y_T\mid x_{1:T}^{(i)})\\ & =\mathcal{P}(y_t,y_{t+1}\mid x_{1:T}^{(i)})\end{array}$$
此时发现，化简后的结果就是关于$y_t,y_{t+1}$的边缘概率分布($x_{1:T}^{(i)}$不是变量，是已知信息)。
$$\begin{array}{rl}{\nabla }_{\lambda }\left[\log \mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )\right]& =\sum _{t=1}^{T-1}\sum _{y_t,y_{t+1}}\left[\sum _{y_1,\cdots ,y_{t-1}}\sum _{y_{t+2},\cdots ,y_T}\mathcal{P}(\mathcal{Y}\mid x_{1:T}^{(i)})\cdot s(y_t,y_{t+1},x_{1:T}^{(i)})\right]\\ & =\sum _{t=1}^{T-1}\sum _{y_t,y_{t+1}}\mathcal{P}(y_t,y_{t+1}\mid x_{1:T}^{(i)})\cdot s(y_t,y_{t+1},x_{1:T}^{(i)})\end{array}$$
观察上式，上式已经被化简成只包含$y_t,y_{t+1}$两个变量的式子。$s$是定义的特征函数，可求；$\mathcal{P}(y_t,y_{t+1}\mid x_{1:T}^{(i)})$使用前向后向算法进行求解。对应概率图表示如下：
由于求解两个隐状态整体的边缘分布，需要空出一个团来。

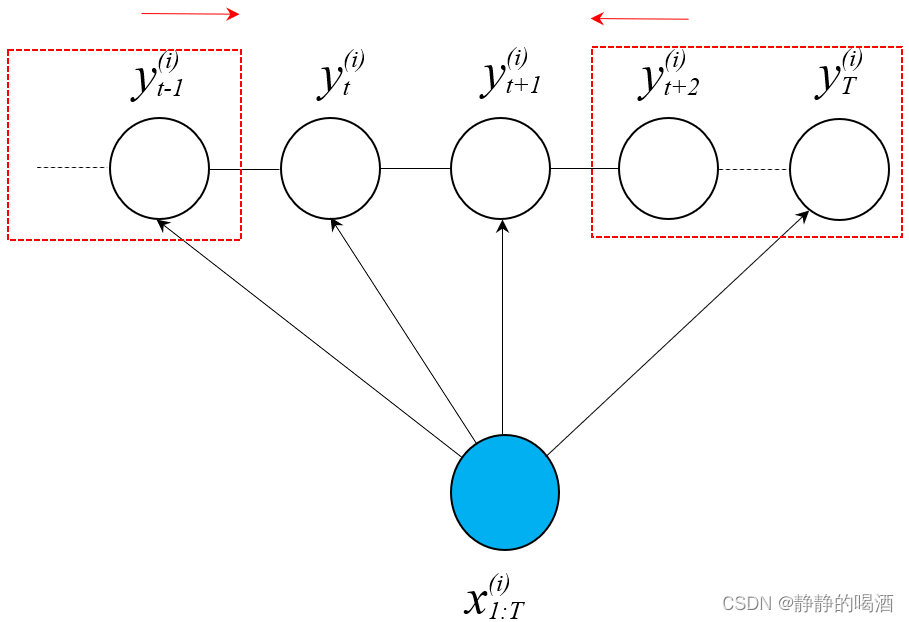
对应公式表示如下：
$$\begin{array}{rl}& \mathcal{P}(y_t,y_{t+1}\mid x_{1:T}^{(i)})\\ & =\sum _{y_1,\cdots ,y_{t-1}}\sum _{y_{t+2},\cdots ,y_T}\frac{1}{\mathcal{Z}}\prod _{t=1}^{T-1}{\psi }_t(y_t,y_{t+1},x_{1:T}^{(i)})\\ & =\frac{1}{\mathcal{Z}}\left\{\left[\sum _{y_1,\cdots ,y_{t-1}}{\psi }_1(y_1,y_2,x_{1:T}^{(i)})\cdots {\psi }_{t-1}(y_{t-1},y_t,x_{1:T}^{(i)})\right]\cdot {\psi }_t(y_t,y_{t+1},x_{1:T}^{(i)})\cdot \left[\sum _{y_{t+2},\cdots ,y_T}{\psi }_{t+1}(y_{t+1},y_{t+2},x_{1:T}^{(i)})\cdots {\psi }_{T-1}(y_{T-1},y_T,x_{1:T}^{(i)})\right]\right\}\\ & =\frac{1}{\mathcal{Z}}\left({\Delta }_{left}\cdot {\psi }_t(y_t,y_{t+1},x_{1:T}^{(i)})\cdot {\Delta }_{right}\right)\{\begin{array}{l}{\Delta }_{left}={\sum }_{y_1}{\psi }_1(y_1,y_2,x_{1:T}^{(i)})\cdots {\sum }_{y_{t-1}}{\psi }_{t-1}(y_{t-1},y_t,x_{1:T}^{(i)})\\ {\Delta }_{right}={\sum }_{t_{t+2}}{\psi }_{t+1}(y_{t+1},y_{t+2},x_{1:T}^{(i)})\cdots {\sum }_{y_T}{\psi }_{T-1}(y_{T-1},y_T,x_{1:T}^{(i)})\end{array}\end{array}$$
设置${\alpha }_t(k)={\Delta }_{left}(y_t=k),{\beta }_{t+1}(j)={\Delta }_{right}(y_{t+1}=j)$，则有：
$$\mathcal{P}(y_t,y_{t+1}\mid x_{1:T}^{(i)})=\frac{1}{\mathcal{Z}}{\alpha }_t(k)\cdot {\psi }_t(y_t,y_{t+1},x_{1:T}^{(i)})\cdot {\beta }_{t+1}(j)$$
至此，关于$\lambda$的梯度结果${\nabla }_{\lambda }\left[\log \mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )\right]$求解过程没有障碍：
$$\begin{array}{rl}{\nabla }_{\lambda }\left[\log \mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )\right]& =\sum _{t=1}^{T-1}\sum _{y_t,y_{t+1}}\mathcal{P}(y_t,y_{t+1}\mid x_{1:T}^{(i)})\cdot s(y_t,y_{t+1},x_{1:T}^{(i)})\\ & =\frac{1}{\mathcal{Z}}\sum _{t=1}^{T-1}\sum _{y_t,y_{t+1}}{\alpha }_t(k)\cdot {\psi }_t(y_t,y_{t+1},x_{1:T}^{(i)})\cdot {\beta }_{t+1}(j)\cdot s(y_t,y_{t+1},x_{1:T}^{(i)})\end{array}$$
最终关于模型参数$\lambda$的梯度${\nabla }_{\lambda }\mathcal{J}(\lambda ,\eta ,x_{1:T}^{(i)})$结果表示如下：
$$\begin{array}{rl}{\nabla }_{\lambda }\mathcal{J}(\lambda ,\eta ,x_{1:T}^{(i)})& =\sum _{i=1}^N\left[\sum _{t-1}^{T-1}s(y_t^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})-{\nabla }_{\lambda }\log \mathcal{Z}(x_{1:T}^{(i)},\lambda ,\eta )\right]\\ & =\sum _{i=1}^N\left[\sum _{t-1}^{T-1}s(y_t^{(i)},y_{t+1}^{(i)},x_{1:T}^{(i)})-\frac{1}{\mathcal{Z}}\sum _{t=1}^{T-1}\sum _{y_t,y_{t+1}}{\alpha }_t(k)\cdot {\psi }_t(y_t,y_{t+1},x_{1:T}^{(i)})\cdot {\beta }_{t+1}(j)\cdot s(y_t,y_{t+1},x_{1:T}^{(i)})\right]\end{array}$$
确定了模型参数$\lambda$的迭代方向，可以通过迭代逼近最优解：
这里就不复述$\eta$的求解过程了。有感兴趣的小伙伴留言交流。
$${\lambda }^{(k+1)}={\lambda }^k+d_{\lambda }\cdot {\nabla }_{\lambda }\mathcal{J}({\lambda }^{(k)},{\eta }^{(k)},x_{1:T}^{(i)})$$

总结

回顾求解模型参数的流程：

• 将原问题转化为最大化目标函数问题，使用梯度上升法；
• 在求解梯度的过程中，利用了对数函数求导；
• 在最终求解边缘概率分布过程中，再次使用了前向后向算法；

至此，条件随机场的相关信息介绍完毕，下一节将返回高斯分布，介绍一些关于高斯分布的基础逻辑。

相关参考：
机器学习-条件随机场（8）-CRF模型-Learning-参数估计