一、CNN与FCN的比较

CNN：在传统的CNN网络中，在最后的卷积层之后会连接上若干个全连接层，将卷积层产生的特征图（feature map）映射成为一个固定长度的特征向量。一般的CNN结构适用于图像级别的分类和回归任务，因为它们最后都期望得到输入图像的分类的概率，如ALexNet网络最后输出一个1000维的向量表示输入图像属于每一类的概率。

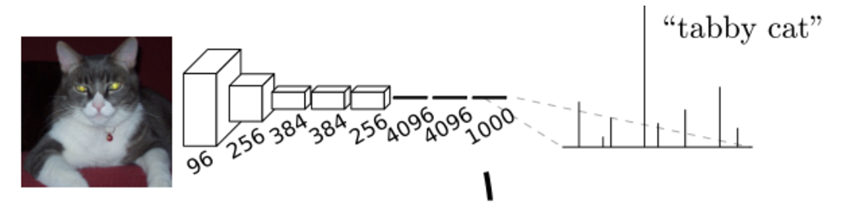
在这里插入图片描述
在CNN中, 猫的图片输入到AlexNet, 得到一个长为1000的输出向量, 表示输入图像属于每一类的概率, 其中在“tabby cat”这一类统计概率最高, 用来做分类任务。

FCN: FCN是对图像进行像素级的分类（也就是每个像素点都进行分类），从而解决了语义级别的图像分割问题。与上面介绍的经典CNN在卷积层使用全连接层得到固定长度的特征向量进行分类不同，FCN可以接受任意尺寸的输入图像，采用反卷积层对最后一个卷基层的特征图（feature map）进行上采样，使它恢复到输入图像相同的尺寸，从而可以对每一个像素都产生一个预测，同时保留了原始输入图像中的空间信息，最后在上采样的特征图进行像素的分类。如下图所示：

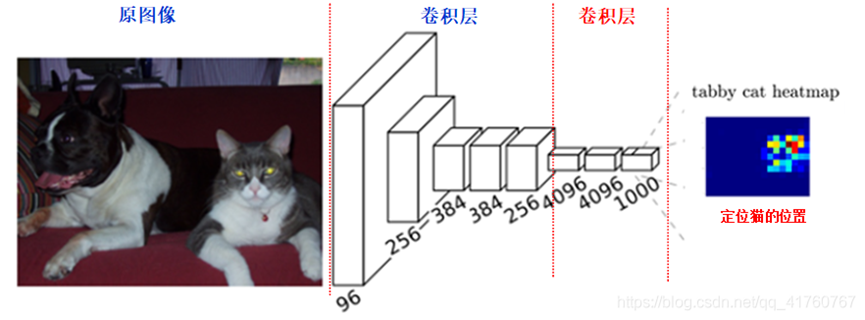
在这里插入图片描述
简单的说，FCN与CNN的区别在于FCN把CNN最后的全连接层换成卷积层，其输出的是一张已经标记好的图，而不是一个概率值。

用于分类的神经网络由卷积层、池化层和最后连接的全连接层组成，经过最后的全连接层后，二维的图像信息被映射为具体的一维类别信息进行输出，得到分类标签。

对于语义分割问题，我们需要的不是具体的类别标签，而是一个二维的分割图，FCN方法丢弃全连接层，并将其换成卷积层，最后输出与原图相同大小的分割图。

论文作者认为：全连接层让目标的位置信息消失了，只保留了语义信息，而将全连接层更换为卷积层可以同时保留位置信息和语义信息。

二、FCN上采样理论讲解

FCN网络一般是用来对图像进行语义分割的，于是就需要对图像上的各个像素进行分类，这就需要一个上采样将最后得到的输出上采样到原图的大小。上采样对于低分辨率的特征图，常常采用上采样的方式将它还原高分辨率，这里陈述上采样的三种方法。

2.1 双线性插值上采样

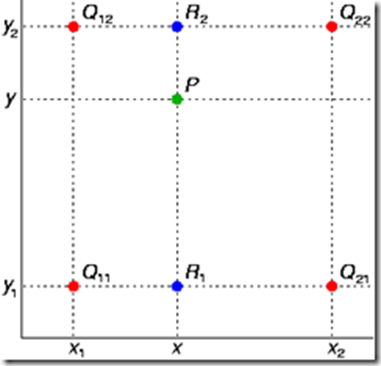
在这里插入图片描述

双线性插值就是做两次线性变换，先在X轴上做一次线性变换，求出每一行的R点：

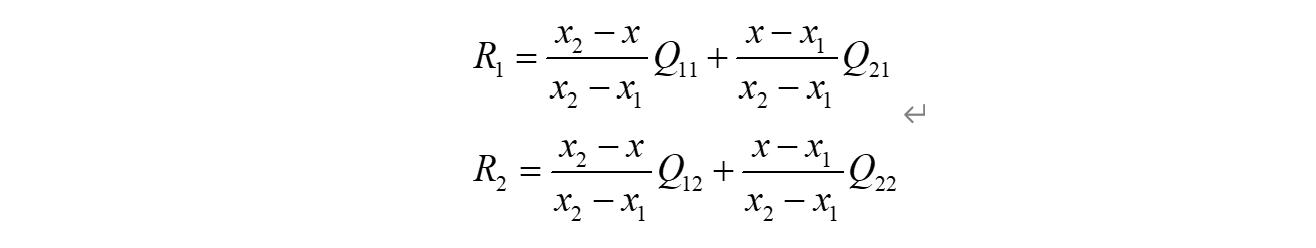
在这里插入图片描述
再在Y轴上做一次线性变换，求该区域的P点：

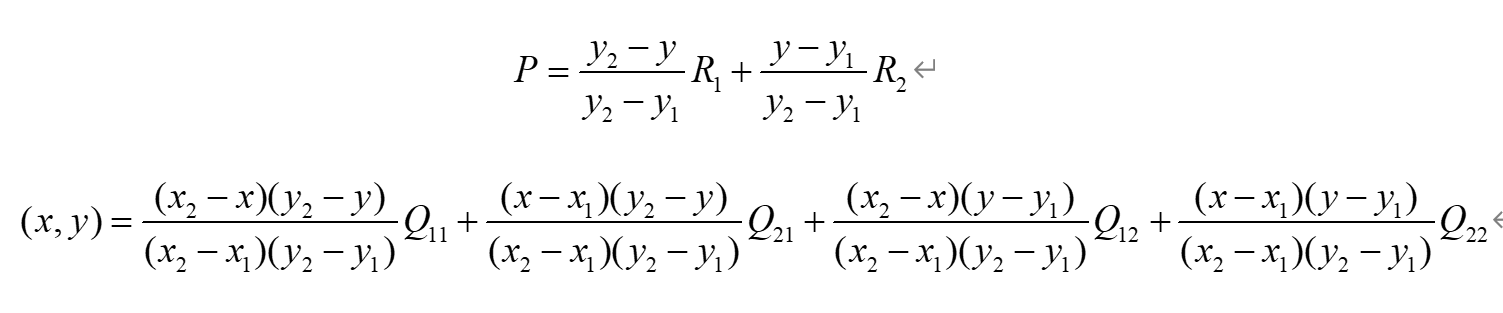
由于图像双线性插值只会用相邻的4个点，因此上述公式的分母都是1。
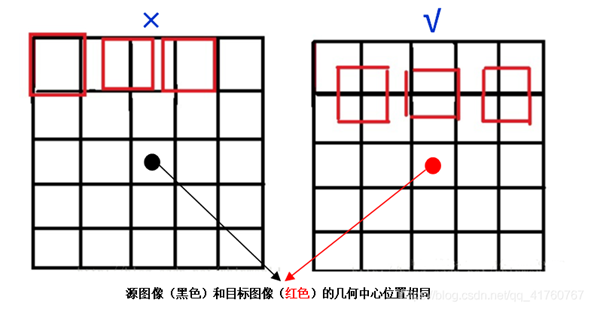
源图像和目标图像几何中心的对齐：

SrcX = (dstX + 0.5) * (srcWidth / dstWidth) - 0.5
SrcY = (dstY + 0.5) * (srcHeight / dstHeight) - 0.5

在这里插入图片描述

2.2 反卷积上采样

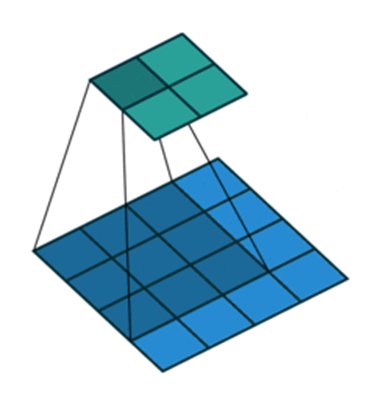
在这里插入图片描述

上采样的过程也是卷积，那么怎么会得到分辨率提高呢？之前我们看卷积时有个保持输出与输入同分辨率的方法就是周围补0。

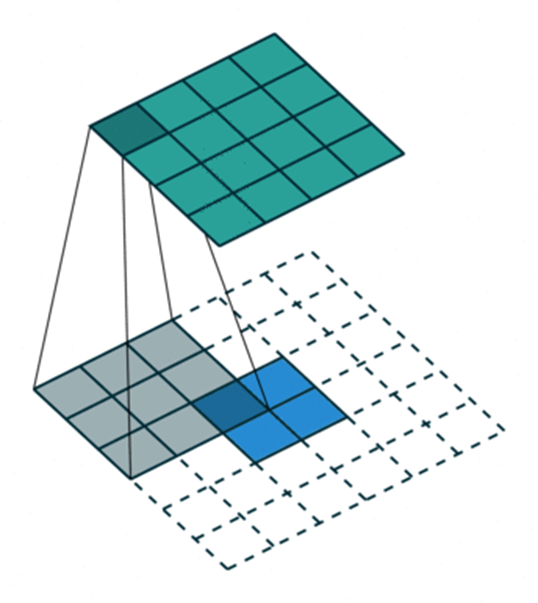
在这里插入图片描述
其实上面这种补0的方法事有问题的，你想一下，只在四周补0会导致最边上的信息不太好，那我们把这个信息平均下，在每个像素与像素之间补0，如下图所示：

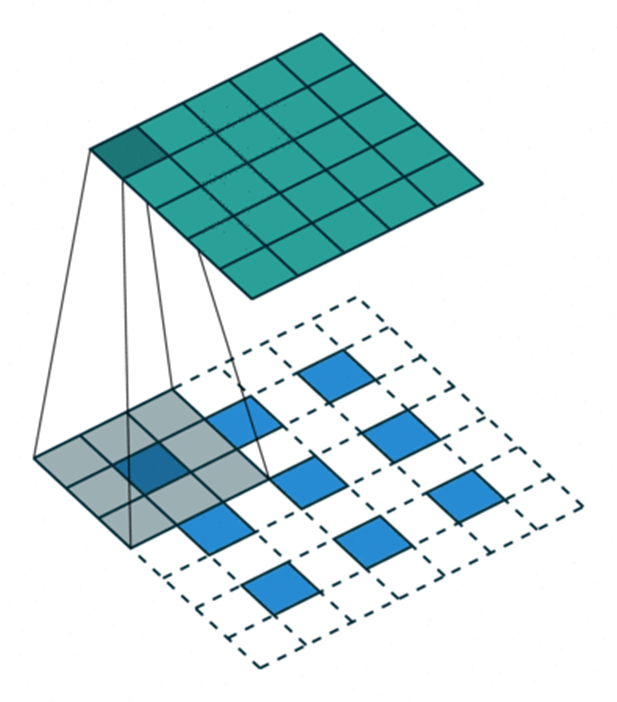
在这里插入图片描述

2.3 反池化上采样

反池化可以用下图来理解，再池化时需要记录下池化的位置，反池化时把池化的位置直接还原，其他位置填0。

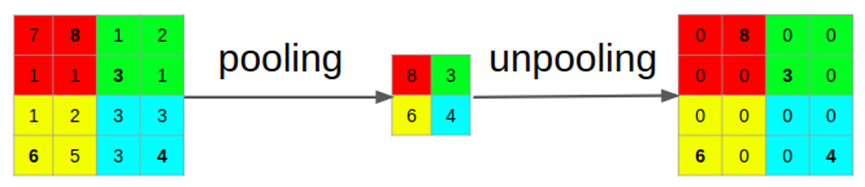
在这里插入图片描述
上面三种方法各有优缺，双线性插值方法实现简单，无需训练；反卷积上采样需要训练，但能更好的还原特征图。

三、FCN的过程

FCN将传统CNN中的全连接层转化成卷积层，对应CNN网络FCN把最后三层全连接层转换成为三层卷积层。在传统的CNN结构中，前5层是卷积层，第6层和第7层分别是一个长度为4096的一维向量，第8层是长度为1000的一维向量，分别对应1000个不同类别的概率。FCN将这3层表示为卷积层，卷积核的大小 (通道数，宽，高) 分别为 (4096,1,1)、(4096,1,1)、(1000,1,1)。看上去数字上并没有什么差别，但是卷积跟全连接是不一样的概念和计算过程，使用的是之前CNN已经训练好的权值和偏置，但是不一样的在于权值和偏置是有自己的范围，属于自己的一个卷积核。因此FCN网络中所有的层都是卷积层，故称为全卷积网络。
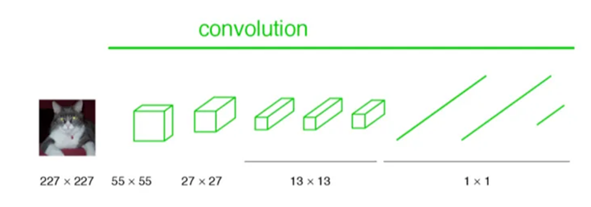
在这里插入图片描述
CNN中输入的图像大小是同意固定resize成 227x227 大小的图像，第一层pooling后为55x55，第二层pooling后图像大小为27x27，第五层pooling后的图像大小为13*13。

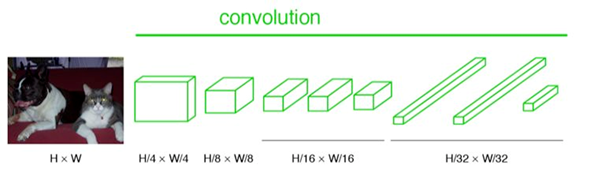
在这里插入图片描述
FCN输入的图像是H*W大小，第一层pooling后变为原图大小的1/4，第二层变为原图大小的1/8，第五层变为原图大小的1/16，第八层变为原图大小的1/32（勘误：其实真正代码当中第一层是1/2，以此类推）。

经过多次卷积和pooling以后，得到的图像越来越小，分辨率越来越低。其中图像到 H/32∗W/32 的时候图片是最小的一层时，所产生图叫做heatmap热图，热图就是我们最重要的高维特诊图，得到高维特征的heatmap之后就是最重要的一步也是最后的一步对原图像进行upsampling，把图像进行放大、放大、放大，到原图像的大小。

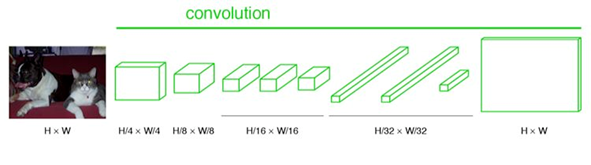
在这里插入图片描述
最后的输出是1000张heatmap经过upsampling变为原图大小的图片，为了对每个像素进行分类预测label成最后已经进行语义分割的图像，这里有一个小trick，就是最后通过逐个像素地求其在1000张图像该像素位置的最大数值描述（概率）作为该像素的分类。因此产生了一张已经分类好的图片，如下图右侧有狗狗和猫猫的图。

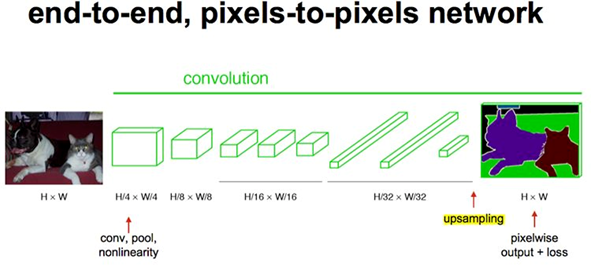
在这里插入图片描述

四、跳级结构

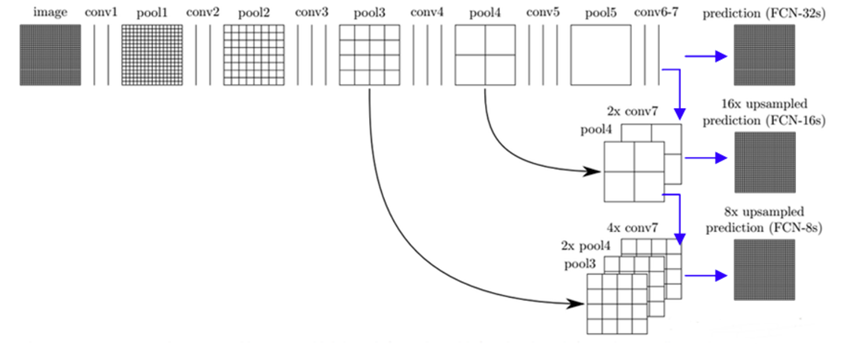
跳级(strip)结构：对第5层的输出执行32倍的反卷积得到原图，得到的结果不是很精确，论文中同时执行了第4层和第3层输出的反卷积操作（分别需要16倍和8倍的上采样），再把这3个反卷积的结果图像融合，提升了结果的精确度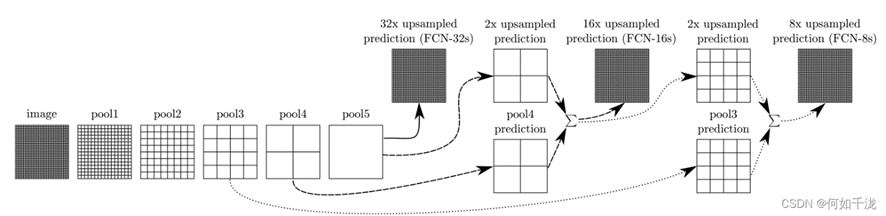：在这里插入图片描述
采用这种方法，能够在保留全局特征的前提下，尽可能使得图像的划分更为精细。

FCN的卷积网络部分可以采用VGG、GoogleNet、AlexNet等作为前置基础网络，在这些的预训练基础上进行迁移学习与fine-tuning，对反卷积的结果跟对应的正向feature map进行叠加输出(这样做的目的是得到更加准确的像素级别分割)，根据上采样的倍数不一样分为FCN-8S、FCN-16S、FCN-32S，图示如下：

对原图像进行卷积 conv1、pool1后原图像缩小为1/2；
之后对图像进行第二次 conv2、pool2后图像缩小为1/4；
继续对图像进行第三次卷积操作conv3、pool3缩小为原图像的1/8，此时保留pool3的featureMap；
继续对图像进行第四次卷积操作conv4、pool4，缩小为原图像的1/16，保留pool4的featureMap；
最后对图像进行第五次卷积操作conv5、pool5，缩小为原图像的1/32;
然后把原来CNN操作中的全连接变成卷积操作conv6、conv7，图像的featureMap数量改变但是图像大小依然为原图的1/32，此时图像不再叫featureMap而是叫heatMap。

现在我们有1/32尺寸的heatMap，1/16尺寸的featureMap和1/8尺寸的featureMap，1/32尺寸的heatMap进行upsampling操作之后，因为这样的操作还原的图片仅仅是conv5中的卷积核中的特征，限于精度问题不能够很好地还原图像当中的特征，因此在这里向前迭代。把conv4中的卷积核对上一次upsampling之后的图进行反卷积补充细节（相当于一个差值过程），最后把conv3中的卷积核对刚才upsampling之后的图像进行再次反卷积补充细节，最后就完成了整个图像的还原。

在这里插入图片描述